浅谈用整体法与隔离法求解连接体问题
2017-06-20安徽省固镇县石湖中学
安徽省固镇县石湖中学 左 桐
一、连接体
利用牛顿运动定律处理的问题中经常出现几个物体用轻绳,轻杆或轻弹簧连在一起或叠放,挤压在一起的一类问题,这类问题中系统中的各物体间有相互作用力,并在相互作用力及其他力的作用下参与运动,这类问题被称为连接体问题,高中阶段主要处理加速度相同(或为零)的连接体问题。
二、连接问题的处理方法
(一)合成法与分解法
将力或速度,加速度进行合成或分解。
(二)整体法与隔离法
1.外力和内力
在使用整体法与隔离法之前,首先要明确外力和内力。如果以物体组成的系统为研究对象,则系统之外的作用力为该系统受到的外力,而系统内各物体间的相互作用力为该系统的内力。
2.整体法
把整个系统作为一个研究对象来分析的方法,不必考虑系统内力的影响,只考虑系统受到的外力,依据牛顿第二定律列方程求解。此方法适用与系统中各部分物体加速度相同的情况。尤其适用于求解系统的加速度。比如,在光滑的水平面上,一水平力F作用在B上,A,B相对静止,求系统中B的加速度?及A受到的摩擦力F?(如下图甲所示)
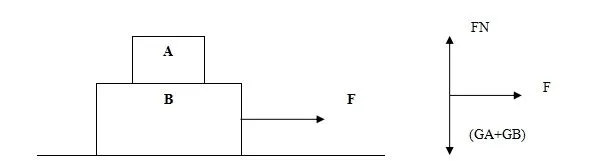
在这个问题中第一问显然用整体法求解方便,因为力F作用于B上后A,B相对静止,可把A,B看作一个整体。A,B间的作用力作为系统内力,在用整体法时,不用分析。则系统在水平方向只受外力F,竖直方向系统所受的重力(GA+GB),和水平面支持力FN是一对平衡力,所以系统所受这三个力的合力即为力F.根据牛顿第二定律,则系统加速度a=F/(mA+mB),方向与F方向相同,水平向右。物体B加速度与系统加速度相同。系统受力分析如上图乙所示。
3.隔离法
把系统中的各个部分(或某一部分)隔离,作为一个单独的研究对象来分析的方法。此时系统内力对隔离出来的物体来说就有可能成为该研究对象的外力,在对该物体受力分析时,就一定要分析上了。求研究对象所受的合力,用牛顿第二定律列方程求解。此方法对于系统内各部分物体加速度相同或不相同均适用,尤其适合于求解系统内力。
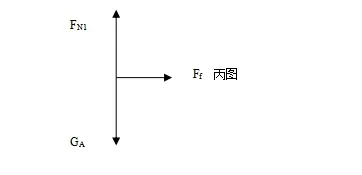
比如,在上例中第二问,求A受到的摩擦力,此种情况下需要用隔离法,把A隔离出来作为研究对象,它受到重力GA和B物体给它的支持力FN1,以及B物体给它的静摩擦力Ff,竖直方向GA和FN1是一对平衡力,所以A所受的三个力的合力即为Ff,由牛顿第二定律得Ff=mA(1),及a=F/(mA+mB)(2),由(1)及(2)得Ff=mAF/(mA+mB),方向水平向右。受力分析如下图丙所示。
三、用整体法和隔离法解答连接体问题
1.用整体法解题的基本步骤
(1)明确研究的系统或运动的过程。
(2)画出系统的受力图和运动过程的示意图。
(3)寻找未知量与已知量之间的关系,选择适当的物理规律列方程求解。
2.运用隔离法解题的基本步骤
(1)明确研究对象或过程,状态,选择隔离对象,选择原则:一是包含待求量,二是所选隔离对象和所列方程数尽可能少,即选择受力少又包含待求量的物体研究。
(2)将研究对象从系统中隔离出来或将研究对象的某状态,某过程从运动的全过程中隔离出来。
(3)对隔离出来的研究对象,过程,状态分析研究,画出某状态下的受力图或某阶段的运动过程示意图。
(4)寻找未知量与已知量之间的关系,选择适当的物理规律列方程求解。
3选用整体法和隔离法求解连接体问题的原则
在解答连接体问题时,决不能把整体法和隔离法对立起来,多数情况下两种方法要配合使用。求各部分加速度相同的连接体的加速度或合力时,优先考虑“整体法”,如果还要求物体之间的作用力,再用“隔离法”。有的问题整体法和隔离法都能解决,在这种情况下一般用整体法更简便。在实际应用中,应根据具体情况,灵活交替使用这两种方法,不应拘泥于固定模式。无论运用整体法还是隔离法,解题的关键还是在于对研究对象进行正确的受力分析。
现就整体法与隔离法的使用分别举例如下:
题型一:用整体法求连接体问题
例1 如下图甲所示,质量为2m的物体A与质量为m的物体B静止于光滑的水平面上,一水平力F作用于A物体,求F作用后A的加速度?
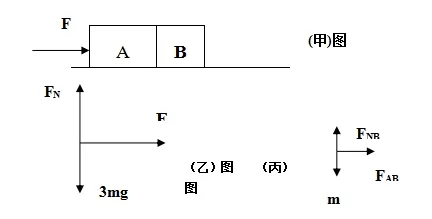
解析:A与B运动状态相同,如果把A与B看作一个整体来研究,对系统进行受力分析如上图乙所示,在水平方向系统只受力F作用,竖直方向系统受重力和水平面的支持力,它们是一对平衡力,显然系统所受合力即为力F,根据牛顿第二定律F=3ma得a=F/3m ,方向水平向右。A加速度与系统加速度相同。
题型二:用隔离法求连接体问题
如果在上题例1中,求:A对B的作用力FAB大小?
解析:本题中因为要求的是系统内力,所以要用隔离法,把B隔离出来研究,受力分析如上图丙所示,B在竖直方向,受重力和水平面给它的支持力是一对平衡力,B在水平方向,只受A给它的作用力FAB ,三力的合力为FAB,根据牛顿第二定律FAB=mBa=ma=mF/3m=F/3
题型三:整体法与隔离法配合使用
例略。
题型四:求系统外力时,先隔离后整体研究
例略。
题型五:求连接体问题时,状整体法与隔离法均可使用,但用整体法更简便
例略。
