多运行方式下风电机组变频器参与次同步相互作用的分析与抑制

边晓燕 施 磊 宗秀红 李东东 符 杨

(1.上海电力学院电气工程学院 上海 200090 2.南方电网深圳供电局有限公司 深圳 518020)



多运行方式下风电机组变频器参与次同步相互作用的分析与抑制

边晓燕1施 磊1宗秀红2李东东1符 杨1

(1.上海电力学院电气工程学院 上海 200090 2.南方电网深圳供电局有限公司 深圳 518020)

大规模风电经串补线路进行远距离传送存在引发次同步相互作用的风险，系统运行方式、串补度及变频器控制参数为主要影响因素。采用概率法和模式分析相结合，分别在含双馈感应型和永磁同步型风电场系统中，研究多运行方式下风电串补系统的次同步相互作用。利用参与因子进行模式识别，研究了串补度对次同步振荡模式及概率稳定性的影响，引入概率灵敏度指标分析起主导作用的变频器PI控制参数，并基于风电机组变频器提出一种鲁棒抑制次同步相互作用的附加阻尼控制策略。仿真结果表明，双馈风电串补系统中易产生次同步控制相互作用，在网侧变频器加装鲁棒DFIG-PSS能实现其有效抑制，而永磁同步风电机组对这一相互作用具有免疫特性。

双馈感应发电机 永磁同步发电机 次同步相互作用 概率灵敏度 电力系统稳定器 次同步概率稳定性

0 引言

我国的风资源主要集中于西部、北部地区，远离负荷中心，串联电容补偿技术是提高远距离输电系统传送能力的常用措施。但风电场经串补线路并网在一定条件下易激发电力系统次同步相互作用(Sub-Synchronous Interaction，SSI)，威胁风电场的安全稳定运行。风电系统SSI问题分为3种类型：次同步扭振相互作用(Sub-Synchronous Torsional Interaction，SSTI)、次同步谐振(Sub-Synchronous Resonance，SSR)和次同步控制相互作用(Sub-synchronous Control Interaction，SSCI)[1]。最先受到人们关注的是20世纪70年代美国Mohave电厂机组因SSR使轴系受损。SSCI是一种新型次同步振荡现象，2009年美国德克萨斯州公布了第一起SSCI事故，一条345 kV传输线因接地故障断线被切除，输电线路串补度从50%上升为75%，风电场电压与电流都出现了次同步振荡，导致风机大面积脱网，内部撬棒电路损坏[2]。因此，次同步相互作用原理和影响因素分析以及如何有效抑制具有重要的现实意义。

目前，国内外针对次同步相互作用的分析与抑制已开展研究。文献[3-6]通过建立双馈风机串补系统的小干扰模型，分别采用结合参与因子的模式分析法和定转子转矩分析法，研究了风速、串补度及变频器PI参数对次同步振荡特性的影响，但并没有提出有效的抑制措施。文献[7]通过特征值灵敏度分析得到风机转子侧变频器(Rotor Side Converter，RSC)电流环比例系数是影响SSI的重要因素，减小该系数可起到一定抑制作用。但是，当该系数减小到一定程度后会破坏风机控制频带宽度，难以满足故障穿越要求[1]。文献[8，9]对风电机组参与SSI抑制进行研究，证明风机变频器采用类似同步发电机附加阻尼控制策略的有效性，文献[10]利用静止同步补偿器(Static Synchronous Compensator，STATCOM)的能力阻尼SSI，因网侧变频器(Grid Side Converter，GSC)的拓扑结构与STATCOM相似，文献[8]在GSC附加阻尼控制为系统提供正阻尼，通过对比加装阻尼控制器前后的相同运行工况来反映SSI抑制效果。

由于风电出力与负荷具有随机波动特性，在某种特定运行工况下设计的SSI阻尼控制器随系统运行状态变化可能不再适用，目前鲜有文献涉及适用于多运行方式下次同步相互作用的分析方法与抑制措施，而且上述文献探讨SSI问题大都针对双馈感应风力发电机组(Doubly Fed Wind Induction Generator，DFIG)，而较少文献涉及永磁同步风力发电机组(Permanent Magnet Synchronous Generator，PMSG)。

本文以DFIG和PMSG风电串补系统为研究对象，考虑了风机出力和同步机出力的不确定性以及负荷随机波动的系统多运行状态，提出概率特征根法与参与因子相结合，对振荡模式进行识别，在得到系统振荡模式的统计属性后，判断模式的概率稳定性。在此基础上，分析补偿度和变频器PI参数对次同步模式的影响，进而为采用鲁棒DFIG-PSS抑制次同步相互作用提供依据，最后将仿真分析结果与无抑制措施时的性能进行了比较。

1 风电场并网次同步相互作用研究

1.1 次同步相互作用分类

根据参与部件不同，SSI可分为SSTI、SSR和SSCI[1，11]，如图1所示。SSTI为风电机组轴系与控制器或者相邻的FACTS 装置控制器之间的相互作用。SSR为风电机组轴系与串联电容补偿输电系统间耦合并在次同步频率下交换能量时电气量与机械量之间的相互作用，其中，SSR又可分为稳态和暂态两种振荡类型，前者包括感应发电机效应(Induction Generator Effect，IGE)和轴系扭振相互作用(Torsional Interaction，TI)，后者包含轴系扭矩放大作用(torque amplification，TA)。SSCI为风电机组变频器与串补系统之间纯电气的相互作用。

图1 次同步相互作用分类Fig.1 Classification of sub-synchronous interactions

1.2 扭振相互作用与次同步控制相互作用

当发电机轴系受到扰动时，轴系扭振模式互补频率与该扭振模式的电气阻尼有密切关系[12]。扰动引起的振荡频率会在定子上产生次同步电压分量，对应的电流分量会造成发电机电磁转矩的变化，当转速偏差量与电磁转矩偏差量之间相角大于90°，产生电气负阻尼，如果其值大于对应扭振模式的机械阻尼，机械系统与电气系统之间会相互激励[13]，产生扭振相互作用。

SSR和SSTI 都是风机轴系参与的相互作用，与传统火电机组不同的是，风机轴系的刚度系数较小，轴系固有扭振频率很低，一般为1～3 Hz，因此，风电机组中并不易发生轴系扭振问题[3]。

SSCI是与轴系无关的次同步相互作用，因此，没有一个固定的轴系振荡频率，其频率随系统运行方式和变频器控制参数的变化而改变。系统受到扰动时发电机定子上产生的次同步电流会在转子上感应出对应的次同步电压分量，又会进一步在定子侧感应出次同步电流分量，当该电流分量与初始扰动电流叠加后，与原有的次同步电流相位差小于90°时，会助增原次同步电流，形成一个作用回路[14]。一方面，变频器结构及其控制参数会对SSCI产生影响，另一方面，在风机变频器附加阻尼控制策略，可以提供阻尼能力，利用风机自身参与SSCI抑制。

1.3 DFIG/PMSG风电场变频器控制系统建模

DFIG和PMSG是目前风电场中两种常用风机类型，大规模集群风电场可以采用容量等值方法等效为单台风机进行研究[8]，DFIG和PMSG等值风机分别经串补线路接入无穷大系统的示意图如图2所示，其中下标s、r分别表示定子、转子分量。

图2 含DFIG/PMSG风电场串补系统示意图Fig.2 Schematic of DFIG/PMSG-based series compensated system

DFIG RSC采用基于定子磁链矢量控制策略，控制框图如图3所示，实现了有功和无功解耦控制，即控制转子电流d轴和q轴分量就可以分别控制DFIG有功功率和输向电网的无功功率。GSC采用基于电网电压定向矢量控制策略，控制框图如图4所示，用于维持变流器中直流母线电压恒定。图4中，Kp和Ki分别为比例和积分时间常数；下标ref表示参考值；x1～x7为变频器状态变量。

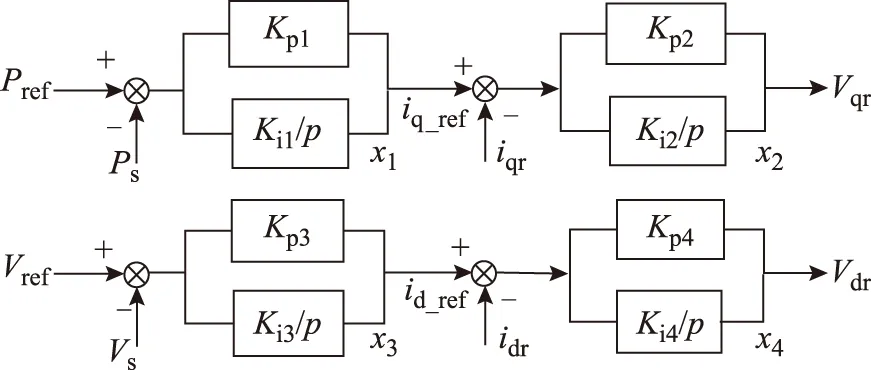
图3 转子侧变频器控制框图Fig.3 Control schematic of RSC

图4 网侧变频器控制框图Fig.4 Control schematic of GSC

PMSG采用全功率变频器，发电机侧变频器(PMSG Side Converter，MSC)和GSC分别采用解耦控制和电网电压定向矢量控制，如图5和图6所示。

图5 发电机侧变频器控制框图Fig.5 Control schematic of MSC

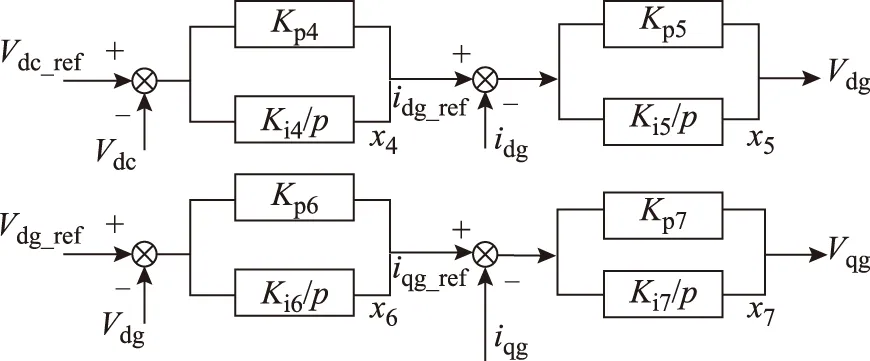
图6 网侧变频器控制框图Fig.6 Control schematic of GSC

2 概率分析方法

2.1 概率特征根及概率分布

将节点电压、节点注入及特征根都视作随机变量，利用概率方法考虑系统运行状态的随机变化特性，通过特征根与电压之间的解析关系，得出阻尼常数和阻尼比的统计属性及概率分布，意在对次同步模式进行概率稳定研究，提出参与因子及概率灵敏度指标分析次同步相互作用，为附加阻尼控制策略提供参考。概率特征根方法的流程如图7所示。

图7 概率特征根方法流程Fig.7 The flow chart of the probabilistic eigenvalue method

对于结构确定的系统，已知节点注入功率，由概率潮流计算[15]可求得节点电压的均值和方差，提供系统的初始状态。将特征根λk与节点电压V之间的非线性函数在V期望值附近进行泰勒展开，由式(1)和式(2)可求得特征根期望和方差。

(1)

(2)

其中，(γk，χk)表示αk和ωk四种组合方式中任意一种。

每一对复特征根λk=αk±jωk对应着一个振荡模式，实部表示该振荡模式的阻尼，虚部反映振荡频率。式(3)定义的阻尼比ξk反映振荡模式的衰减特性，是判别电力系统稳定性的一个重要指标。

(3)

(4)

特征根的前两阶矩可由节点电压的均值和协方差得到，高阶累加量用混合中心矩和半不变量表示[16]，采用Gram-Charlier级数展开求得αk和ξk的概率密度f(αk)和f(ξk)，分布概率由式(5)求得。

(5)

2.2 参与因子

(6)

2.3 概率灵敏度指标

(7)

(8)

(9)

3 算例

3.1 算例模型简介

9月27日，水利部党组副书记、副部长、国务院第一次全国水利普查领导小组办公室主任矫勇主持召开国务院水利普查办第十八次主任办公会议，听取国务院水利普查办近期工作汇报，部署下一阶段工作。

采用图8所示的改进4机2区域算例系统[20]进行仿真，同步发电机G1～G4采用六阶模型[21]。由80台风机组成的风电场等效为1台风力发电机组G5，经35kV/110kV升压变压器和串补线路接入系统，补偿度选取符合实际工程取值范围的60%[22]。算例1采用1.5MW双馈感应风电机组[16]，算例2采用相同容量的永磁同步风电机组[23]。本文研究中随机变量的概率特性由累积概率密度曲线获得[24]。

图8 含风电场5机2区域系统Fig.8 A five-machine two-area system with wind farm integrated

3.2 算例1：双馈感应型风电场并网的特征根概率

不含风电场的算例系统共有27对特征根，都位于复平面的左半平面，系统是概率稳定的。双馈风电场并入电力系统后新增振荡模式的概率特征见表1。根据计算公式f=ω/(2π)，模式1的振荡频率为16.39 Hz，属于次同步振荡范围。由表1可以看出，模式1动态衰减特性差，并缺少足够的稳定性。为进一步对模式识别，计算各振荡模式的参与因子见表2。

表1 含双馈风电场系统新增特征根概率

振荡模式是由双馈风机引起，与四台同步发电机无关，表2列出了风机状态变量的参与因子，模式1中轴系状态变量参与因子非常小，直流电容电压的偏差量ΔVdc和变频器的状态变量Δx7与该模式强相关，因此，模式1为SSCI模式，振荡可能是由变频器网侧有功功率控制环或是无功电流控制环引入的。模式2和模式4振荡频率分别为2.29 Hz和0.86 Hz，且都与发电机电气量有很强的相关性，为低频振荡模式。

模式3主要是轴系状态变量参与，其他状态变量参与程度很小。改变轴系固有参数，仅模式3发生了变化，对模式1、模式2和模式4无任何影响，因此可判断模式3为TI模式，由轴系的固有特性决定[6]。改变轴系固有参数Ksh，振荡模式的概率特征见表3。由表3可见，Ksh越大，虚部的幅值明显增大，概率阻尼比下降，TI模式的概率稳定性变差。当串补系统中电气振荡频率接近扭振互补频率时，机网相互作用会激发轴系扭振。

表2 参与因子

表3 轴系固有参数变化时的特征根概率(模式3)

3.3 算例2：永磁同步型风电场并网的特征根概率

永磁同步型风电场并网后新增的特征根概率见表4，计算振荡模式的参与因子如图9所示(为了易说明，图9仅列出了部分有具有代表性的量)。

表4 含永磁风电场系统新增特征根概率

图9 参与因子Fig.9 Participation factor

结合特征根概率和图9a可知，模式5中变频器状态变量占主导作用，为SSCI模式，但并没有发生SSCI。模式6和模式7发电机电气量的参与最大，振荡频率分别为1.66 Hz和1.08 Hz，为低频振荡模式。分析图9b可知，模式8是变频器与轴系之间的相互作用，为SSTI模式。与双馈风电场串补系统相比，永磁风电场串补系统具有较高的概率稳定性。

随着串补度的变化，系统阻尼和振荡频率也会改变，不同串补度情况下的次同步模式见表5。

表5 不同串补度下的特征根概率

观察表5可知，针对双馈风机串补系统，串补度对SSCI模式的影响大于对TI模式的影响，随着串补度增大，振荡模式的概率阻尼比变小，概率稳定性变差。永磁同步风机在45%、60%和75%的串补度下并没有发生次同步相互作用，模式阻尼随串补度增大而减小，当串补度大于临界值[3，25]，模式阻尼增加，但概率阻尼比仍在减小，当补偿度达到90%，模式5的振荡频率为14.68 Hz，发生SSCI，串补度增大使扭振模式概率特性变差，仿真结果说明线路串补度越大，系统SSI风险越大。在实际工程中，永磁同步风机一般不会发生SSI。

3.5 变频器控制参数对SSCI模式的影响

本节在系统多运行方式下，求取特征根对变频器PI控制参数的PSI，见表6，反映了控制参数对SSCI模式的影响。

PSI反映了特征根的变化趋势，其值大小表征了模式对参数变化的敏感程度。由表6可以看出，增益Kp对SSCI的影响大于时间常数Ki的影响，SSCI与双馈风电机组转子侧变频器中增益Kp2和网侧变频器增益Kp7紧密有关，两者PSI的符号都为负，说明Kp与系统稳定性负相关，减小Kp可提高次同步模式的概率稳定性。永磁同步风电机组变频器参数对SSCI模式的PSI很小，证明该类型风电机组对SSCI具有免疫特性。

表6 SSCI模式对变频器PI参数的PSI

4 次同步控制相互作用抑制研究

SSCI无机械系统参与，系统对振荡的阻尼很小，在双馈风电系统变频器加装PSS，通过改进控制系统，利用DFIG提供阻尼转矩参与抑制SSCI，能够同时兼顾抑制效果和风机控制性能[26]。根据参与因子(见表2)和概率灵敏度(见表6)，选择网侧变频器无功电流控制环作为DFIG-PSS的接入位置，SSCI模式与ΔVdc强相关并且具有高的概率灵敏度，选取ΔVdc作为反馈输入信号引入到变频器中，如图4所示。PSS的结构如图10所示，其中，KPSS为增益；T1和T2为相位补偿时间常数；Tw为隔直时间常数，一般取5～10 s。DFIG-PSS通过输入信号使风电机组输出与系统振荡相关的阻尼转矩，抑制次同步频率下定子电流正反馈，进而利用DFIG阻尼次同步相互作用[27]。

图10 PSS模型Fig.10 Module of PSS

DFIG-PSS的参数为：KPSS=12.5，Tw=10 s，T1=0.217 s，T2=0.106 s。加装DFIG-PSS后，特征根概率见表7。可见，TI模式(模式3)的P{α<0} 和P{ξ>0.1}均为100%，是概率稳定的。与未加抑制措施时特征根概率(见表1)相比，SSCI模式(模式1)的阻尼比明显增加，实部向远离虚轴的方向移动，次同步概率稳定性得到显著改善。加装DFIG-PSS前后，SSCI模式实部和阻尼比的概率密度曲线对比如图11和图12所示。

表7 加装DFIG-PSS后特征根概率

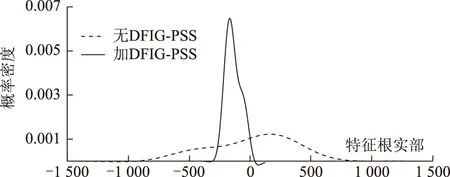
图11 模式1实部概率密度曲线Fig.11 Probability density curves of real parts of mode 1

图12 模式1阻尼比概率密度曲线Fig.12 Probability density curves of PDR of mode 1

由图11可以看出：双馈系统次同步模式的阻尼常数有大于一半的概率落于虚轴右侧的不稳定区域，加装DFIG-PSS使SSCI模式实部概率密度曲线向左移动，并且变得集中，体现了抑制SSCI的有效性。

由图12可以看出：不采用抑制措施时阻尼比的取值跨度大，有接近一半的概率会取到负值，意味着特征根实部为正数，次同步模式不稳定。加装DFIG-PSS后，阻尼比概率取值集中，SSCI模式处于正阻尼状态，改善了双馈风电场经串补线路接入电力系统的次同步概率稳定性。

为了进一步探讨加装抑制措施对次同步控制相互作用的抑制效果，选取含双馈风电场串补系统为例，利用DigSILENT/PowerFactory进行暂态时域仿真。选取风速为7 m/s的运行工况，假设系统在0 s时并网点发生三相短路故障，持续时间为0.075 s。在网侧变频器加装鲁棒DFIG-PSS时的系统动态特性与未加抑制措施进行对比，如图13所示。可以看出，无抑制措施时，系统发生次同步振荡且发散速度很快，加装DFIG-PSS快速有效地抑制了次同步振荡，保证风电场的安全稳定运行。

图13 有无抑制措施时系统动态响应Fig.13 System dynamic response with and without suppression countmeasures

5 结论

本文利用概率特征根分析法对多运行方式下风电场经串补线路并网出现的次同步相互作用进行研究，分析了串补度和变频器控制参数对次同步特性的影响，在此基础上，提出了在DFIG网侧变频器加装鲁棒PSS的抑制方法，得到如下结论：

1)通过参与因子对次同步模式进行识别，包括由轴系引起的扭振模式和变频器引起的SSCI模式，根据阻尼常数和阻尼比两种概率指标判断次同步模式稳定程度。

2)永磁同步风电机组对次同步相互作用具有免疫特性，串补度增大会使振荡模式特性变差，当超过临界串补度后会诱发次同步振荡。因机组结构和控制策略不同，相同串补度下的双馈串补系统更容易激发次同步相互作用，且随着补偿度增大，次同步概率稳定性变差。

3)采用概率灵敏度指标分析变频器控制参数对SSCI模式的影响，转子侧与网侧变频器电流内环比例系数与SSCI模式负相关，且相关程度大，系数增大会加剧SSCI，分析结论为设计鲁棒DFIG-PSS抑制次同步相互作用提供依据。

4)比较加装DFIG-PSS前后阻尼常数和阻尼比的概率密度曲线，结果验证了SSCI抑制的有效性，在不影响其他振荡模式稳定性情况下，改善了多运行方式下系统小扰动次同步概率稳定性。

[1] Leon A E，Solsona J.Sub-synchronous interaction damping control for dfig wind turbines[J].IEEE Transactions on Power Systems，2015，30(1)：419-428.

[2] Adams J，Carter C，Huang S H.ERCOT experience with sub-synchronous control interaction and proposed remediation[C]//IEEE PES Transmission and Distribu-tion Conference and Exposition(T&D)，Orlando，FL，United States，2012：1-5.

[3] Fan Lingling，Kavasseri R，Miao Zhixin，et al.Modeling of DFIG-based wind farms for SSR analysis[J].IEEE Transactions on Power Delivery，2010，25(4)：2073-2082.

[4] 董晓亮，谢小荣，韩英铎，等.基于定转子转矩分析法的双馈风机次同步谐振机理研究[J].中国电机工程学报，2015，35(19)：4861-4869. Dong Xiaoliang，Xie Xiaorong，Han Yingduo，et al.Mechanism study of DFIG-related SSR based on separate stator and rotor torque analysis[J].Proceedings of the CSEE，2015，35(19)：4861-4869.

[5] Su Junlin，Shi Libao，Yao Liangzhong，et al.A comparative sub-synchronous resonance analysis of grid-connected doubly fed induction generator based and permanent magnet synchronous generator based wind farms[J].Electric Power Components & Systems，2015，43(7)：792-809.

[6] Suriyaarachchi D H R，Annakkage U D，Karawita C，et al.A procedure to study sub-synchronous interactions in wind integrated power systems[J].IEEE Transactions on Power Systems，2013，28(1)：377-384.

[7] 董晓亮，谢小荣，杨煜，等.双馈风机串补输电系统次同步谐振影响因素及稳定区域分析[J].电网技术，2015，39(1)：189-193. Dong Xiaoliang，Xie Xiaorong，Yang Yu，et al.Impacting factors and stable area analysis of subsynchronous resonance in DFIG based wind farms connected to series-compensated power system[J].Power System Technology，2015，39(1)：189-193.

[8] Fan Lingling，Miao Zhixin.Mitigating SSR using DFIG-based wind generation[J].IEEE Transactions on Sustainable Energy，2012，3(3)：349-358.

[9] Zhao B，Li H，Wang M，et al.An active power control strategy for a DFIG-based wind farm to depress the subsynchronous resonance of a power system[J].International Journal of Electrical Power & Energy Systems，2015，69：327-334.

[10]Bak-Jensen B，El-Moursi M S，Abdel-Rahman M H.Novel STATCOM controller for mitigating SSR and damping power system oscillations in a series compensated wind parks[J].IEEE Transactions on Power Electronics，2010，25(2)：429-441.

[11]高本锋，刘晋，李忍，等.风电机组的次同步控制相互作用研究综述[J].电工技术学报，2015，30(16)：154-161. Gao Benfeng，Liu Jin,Li Ren，et al.Studies of sub-synchronous control interaction in wind turbine generators[J].Transactions of China Electrotechnical Society，2015，30(16)：154-161.

[12]Milanovic J V，Adrees A.Identifying generators at risk of SSR in meshed compensated AC/DC power networks[J].IEEE Transactions on Power Systems，2013，28(4)：4438-4447.

[13]陈武晖，程欣，汪旎，等.次同步扭振互作用机制解析[J].电网技术，2016，40(4)：1174-1179. Chen Wuhui，Cheng Xin，Wang Ni，et al.Insight into mechanism of subsynchronous torsional interaction[J].Power System Technology，2016，40(4)：1174-1179.

[14]张剑，肖湘宁，高本锋，等.双馈风力发电机的次同步控制相互作用机理与特性研究[J].电工技术学报，2013，28(12)：142-149. Zhang Jian, Xiao Xiangning, Gao Benfeng，et al.Mechanism and characteristic study on sub-synchronous control interaction of a DFIG-based wind-power generator[J].Transactions of China Electrotechnical Society，2013，28(12)：142-149.

[15]Bian X Y，Huang X X，Wong K C，et al.Improvement on probabilistic small-signal stability of power system with large-scale wind farm integration[J].International Journal of Electrical Power & Energy Systems，2014，61：482-488.

[16]边晓燕，耿艳，李学武，等.风电并网系统小干扰概率稳定性分析与改善[J].电力系统保护与控制，2015，43(20)：1-7. Bian Xiaoyan，Geng Yan，Li Xuewu,et al.Probabilistic small-signal stability analysis and improve-ment of power system with wind farm integration[J].Power System Protection and Control，2015，43(20)：1-7.

[17]Wang K W，Chung C Y，Tse C T，et al.Multimachine eigenvalue sensitivities of power system parameters[J].IEEE Transactions on Power Systems，2000，15(2)：741-747.

[18]Chung CY，Wang K W，Tse C T.Probabilistic eigenvalue sensitivity analysis and PSS design in multi-machine systems[J].IEEE Transactions on Power Systems，2003，18(4)：1439-1445.

[19]边晓燕，周歧斌，王克文，等.基于概率法的静止无功补偿器设计[J].电力系统保护与控制，2009，37(20)：18-22. Bian Xiaoyan，Zhou Qibin，Wang Kewen，et al.Robust SVC controller designed by probabilistic method [J].Power System Protection and Control，2009，37(20)：18-22.

[20]张子泳，胡志坚，刘宇凯.计及广域信号时变时滞影响的大型双馈风力发电系统附加鲁棒阻尼控制[J].电工技术学报，2014，29(4)：246-255. Zhang Ziyong，Hu Zhijian，Liu Yukai，et al.Additional robust damping control of large scale DFIG-based wind power generation system with widearea signals′ timevarying delay influence [J].Transactions of China Electrotechnical Society，2014，29(4)：246-255.

[21]Kundur P.Power system stability and control[M].New York：McGraw-hill，1994：130-157.

[22]岑炳成，刘涤尘，董飞飞，等.抑制次同步振荡的SVC非线性控制方法[J].电工技术学报，2016，31(4)：129-135. Cen Bingcheng，Liu Dichen，Dong Feifei，et al.nonlinear control method of static var compensator for damping subsynchronous oscillation [J].Transactions of China Electrotechnical Society，2016，31(4)：129-135.

[23]鞠平.电力系统建模理论与方法[M].北京：科学出版社，2010：315-331.

[24]Bian X Y，Geng Y，Lo K L，et al.Coordination of PSS and SVC damping controller to improve probabilistic small-signal stability of power system with wind farm integration[J].IEEE Transactions on Power Systems，2016，31(3)：2371-2382.

[25]杨帆，王西田，陈陈.串联补偿输电系统次同步谐振的电气模态阻尼的参数敏感性分析[J].华东电力，2005，33(6)：22-27. Yang Fan，Wang Xitian，Chen Chen.Subsynchronous resonance electrical mode dampings parametric sensitivity series compensation[J].East China Electric Power，2005，33(6)：22-27.

[26]张祥宇，付媛，王毅，等.含虚拟惯性与阻尼控制的变速风电机组综合PSS控制器[J].电工技术学报，2015，30(1)：159-169. Zhang Xiangyu，Fu Yuan，Wang Yi，et al.Integrated PSS controller of variable speed wind turbines with virtual inertia and damping control[J].Transactions of China Electrotechnical Society，2015，30(1)：159-169.

[27]杨琳，肖湘宁.电力系统稳定器相位补偿方式对次同步振荡的影响[J].电力系统保护与控制，2014，42(12)：1-7. Yang Lin，Xiao Xiangning.Impact of phase compensa-tion methods of power system stabilizer on subsynchronous oscillation[J].Power System Protection and Control，2014，42(12)：1-7.

(编辑 张玉荣)

Analysis and Mitigation of Wind Turbine Converters in Sub-Synchronous Interaction under Multi-operating Conditions

BianXiaoyan1ShiLei1ZongXiuhong2LiDongdong1FuYang1

(1.School of Electric Power Engineering Shanghai University of Electric Power Shanghai 200090 China 2.Shenzhen Power Supply Bureau of China Southern Power Grid Shenzhen 518020 China)

Large scale wind power transmitted by series compensated lines are susceptible to the sub-synchronous interaction(SSI)in long distance.System operating conditions，series compensation degree and PI parameters of the converter control system are the major influence factors on the power system sub-synchronous stability.This paper presents a probabilistic approach combined with modal analysis to study the SSI issues respectively on doubly fed induction generator(DFIG)system and permanent magnet synchronous generator(PMSG)wind farm system Participation factor(PF)is utilized to analyze the state variables involved in the SSI for mode identification.The impacts of series compensation degree on the oscillation modes are investigated，and then，probabilistic sensitivity index(PSI)is proposed to study the dominant converter control parameters on the SSI，a robust supplementary damping control strategy based on wind turbine converter is presented to exploit the SSCI suppression capability.Obtained results show that DFIG-based wind turbine is highly sensitive to the SSCI，a robust power system stabilizer(PSS)is supplemented to the DFIG grid side converter for SSCI mitigation over a large and pre-specified set of operating conditions，the effectiveness of the proposed approach is validated，whereas，PMSG-based wind turbine is verified to be immune to that interaction.

Doubly fed induction generator(DFIG)，permanent magnet synchronous generator(PMSG)，sub-synchronous interaction(SSI)，probabilistic sensitivity index(PSI)，power system stabilizer(PSS)，sub-synchronous probabilistic stability

上海市教育发展基金会和上海市教育委员会“曙光计划”(15SG50)和上海绿色能源并网工程技术研究中心基金(13DZ2251900)资助项目。

2016-06-5-16 改稿日期2016-07-29

TM315；TM712

边晓燕 女，1976年生，博士，教授，研究方向为电力系统稳定与控制、风力发电。

E-mail：kuliz@163.com

施 磊 女，1991年生，硕士研究生，研究方向为风电并网系统小干扰次同步相互作用分析与改善。

E-mail：shilei0913@126.com(通信作者)