基于电压内积的带并联电抗器输电线路单相自适应重合闸

罗勋华 黄 纯 江亚群 汤 涛 陈 宏

(1.湖南大学电气与信息工程学院 长沙 410082 2.湖南省电力公司科学研究院 长沙 410007)



基于电压内积的带并联电抗器输电线路单相自适应重合闸

罗勋华1黄 纯1江亚群1汤 涛1陈 宏2

(1.湖南大学电气与信息工程学院 长沙 410082 2.湖南省电力公司科学研究院 长沙 410007)

针对带并联电抗器的超高压输电线路，提出一种基于电压内积的单相自适应重合闸实现方案。在线路发生单相接地故障且故障相两端断路器跳开后，求出健全相电压和与故障相端电压的内积为始化内积，健全相电压和与故障相端电压一阶导数电压的内积为补偿内积。对于永久性故障，经短暂态后，始化内积小于补偿内积，两内积曲线不会出现交点。对于瞬时性故障，在二次电弧初始阶段，始化内积小于补偿内积；随着电弧电阻增加，始化内积逐渐增加，补偿内积逐渐减小，两内积曲线出现交点；在恢复电压阶段，两内积呈低频振荡曲线且相位相差90°，并相互交错再次出现交点。基于上述现象，通过两内积曲线是否出现交点来区别永久性和瞬时性故障，并当出现第二个交点时可以确定瞬时性故障已进入恢复电压阶段。该方法不需要整定，在断路器单相跳开后启动判据，实现简便，不需要频域计算、不受低频振荡分量的影响。EMTP仿真和实际录波数据验证了其正确性和可行性。

输电线路 自适应重合闸 故障电弧 内积

0 引言

多数超高压架空输电线路故障是电弧性的瞬时性单相接地故障，采用单相自动重合闸能有效提高电力系统运行的可靠性和稳定性。目前采用的是固定时间间隔直接重合方案，当重合于永久性故障或瞬时性故障未熄弧阶段时，将造成重合闸失败，给电力系统带来严重的二次冲击。

超高压架空输电线路一般带有并联补偿电抗器，为提高其重合闸成功率，学者们研究带并联电抗器的线路自适应重合闸方法[1]，以实现永久性故障闭锁重合闸，瞬时性故障熄弧后发出重合闸命令。

输电线路从发生瞬时性故障至故障相跳闸期间为一次电弧阶段[2]。文献[3，4]利用一次电弧阶段故障相端电压和电流的基波和三次谐波分量建立各序网电压回路方程，通过求解电弧电压或电弧电阻，在断路器跳闸前快速判断故障性质，但只能用于闭锁永久性故障，不能检测瞬时性故障的熄弧时间。

当故障相两端跳闸后，进入二次电弧阶段。二次电弧电流值小，电弧电压失真呈现方波特性，含有大量的奇次谐波[5]。文献[6，7]利用故障相端电压的高频特性识别故障性质，但未考虑电容式电压互感器高频传变性能的影响。

当二次电弧熄灭，进入恢复电压阶段。相间电容存储的直流电压在并联电抗和线路电容形成的回路上衰减振荡，恢复电压含有自由分量，电压波形呈拍频特性。文献[8，9]基于拍频幅值包络提出电压幅值判据，但拍频电压幅值包络线的最大值与并联电抗器补偿度有关。文献[10，11]利用流过并联电抗器与中性点小电抗电流的幅值比来识别永久性故障，但电流工频分量幅值的计算受自由分量的影响。文献[12]建立瞬时性故障熄弧后模型，利用并联电抗器和中性点小电抗的电感参数的求解值与真实值之间的差异来识别故障性质，识别方程复杂，运算量大。文献[13，14]采用故障相并联电抗器电流或恢复电压工频周波内的积分获取自由分量来识别故障性质，该判据在实际应用时必须在二次电弧熄灭之后，而二次电弧熄弧时间未知，因此该判据受熄弧时间长短的制约。

上述方法侧重于故障性质的识别，对实时性没有明确要求[15]，判据启动时间模糊，整定阈值与线路参数、补偿度等有关。鉴于这些不足，本文在故障相电压与健全相电压和的工频相位关系基础上[16]，提出一种基于电压内积的单相重合闸方案。

该方案以健全相电压和与故障相端电压的内积作为始化内积，以健全相电压和与故障相端电压一阶导数电压的内积作为补偿内积，通过两内积曲线的交点来区别故障性质和判断故障熄弧。该方法不需要整定，能在永久性故障下可靠闭锁，理论上最快在故障熄弧后约半个拍频周期内准确判断熄弧。方案采用时域计算方法，避免了自由分量对频域求解的影响，计算量小，便于实现；在断路器单相跳开后启动判据，不受熄弧时间的影响。EMTP仿真和实际录波数据验证了其可行性和优越性。

1 不同故障性质下的内积特性分析

假定系统正常运行时电压相位超前于电流相位角度为j(cosj>0.9)，以A相电流为参考相量，初始相位为零，系统角频率为ω，则A相电压ua和电流ia的瞬时表达式为

(1)

(2)

式中，I1、V1分别为系统正常运行时的电流、电压有效值。

下面将在此基础上讨论瞬时性故障下不同阶段以及永久性故障下始化内积与补偿内积的表达式。

1.1 瞬时性故障二次电弧阶段

(3)

式中，Z=jωLm//[1/(jω2Cm)]。由于并联电抗器通常采取欠补偿运行方式，所以补偿后线路相间等效阻抗Z呈容性。

图1 二次电弧阶段故障相端电压Fig.1 Voltage of fault phase during secondary arc period

(4)

此时故障相端电压瞬时表达式ua(t)近似为

(5)

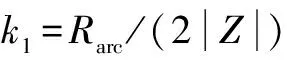
(6)

定义健全相电压和与故障相端电压的瞬时值乘积为p1(t)，与故障相端电压的一阶导数电压的瞬时值乘积为p2(t)，则有

p1(t) =us(t)ua(t)

(7)

(8)

从式(7)和式(8)可以看出，p1(t)、p2(t)都只含有直流分量和两倍工频的高频分量。通过一个周波的积分运算可以完全滤除高频分量，保留其中的直流部分作为自适应重合闸判别的输出量。

(9)

(10)

式中，T0为工频周期；P1(t)与P2(t)分别为两电压内积，即始化内积与补偿内积。

始化内积P1(t)与补偿内积P2(t)可以通过故障相端电压与其一阶导数电压相量在健全相电压和相量上的投影得到，如图2所示。从图2中可看出P1(t)幅值小于P2(t)幅值。

图2 二次电弧阶段电压相量图Fig.2 Voltage phase diagrams under secondary arc period

1.2 瞬时性故障恢复电压阶段

二次电弧阶段，电弧阻值随着电弧拉长逐渐增加，直至熄弧后电弧电阻变为近似无穷大。随后进入恢复电压阶段，可用图3所示等效电路近似求出故障相端电压工频分量为

(11)

式中，Z0=jωL0//[1/jωC0]，Z0与Z都呈容性。

图3 恢复电压阶段故障相电容耦合电压Fig.3 Voltage of fault phase on recovery voltage period

根据式(11)可知在恢复电压阶段，由工频分量产生的电容耦合电压的瞬时值的表达式为

(12)

二次电弧一般在潜供电流过零点附近熄弧，在相间容性回路的作用下，充电电压达到峰值，并在储能元件构成的回路中开始振荡，形成自由分量。自由分量幅值与工频分量近似相等，频率接近工频，使得恢复电压波形呈现拍频特性。

大量仿真和实际故障录波数据表明，恢复电压从拍频波形的包络幅值最小处开始出现，由此可见自由分量与工频分量初始相位相反，瞬时值表达式可以近似为

(13)

式中，ω′为自由振荡频率。

因此，故障相端电压在恢复电压阶段的瞬时值表达式近似为

(14)

则其一阶导数电压的瞬时值表达式为

(15)

由此可见，在恢复电压阶段，两电压瞬时值的乘积p1(t)、p2(t)的一般表达式为

p1(t) =us(t)ua(t)

cos(ωt-ω′t-θ2)]

(16)

p2(t) =us(t)ua(t)

sin(ωt-ω′t-θ2)]

(17)

可以看出，在恢复电压阶段p1(t)、p2(t)中除了含有两倍工频分量与直流分量外，还含有接近两倍工频的高频分量和接近直流的低频分量。由前分析可知，电压内积运算与电压瞬时值乘积通过均值滤波器等效。均值滤波器的幅频特性如图4所示，其对高频分量有很强的抑制作用，可近似认为只有直流分量和低频部分被保留下来，θ2约为0°，因此，两电压内积分别近似为

(18)

(19)

图4 均值滤波器幅频特性Fig.4 Magnitude-frequency response of averaging filter

从式(18)和式(19)可以得出，在恢复电压阶段，P1(t)与P2(t)近似为低频振荡正弦信号且相位相差90°，因此两输出量曲线相互交错存在交点。

1.3 永久性故障

(20)

(21)

式中，k3=Zml。

此时，ua(t)的一阶导数电压瞬时表达式为

(22)

永久性故障下p1(t)、p2(t)的瞬时表达式分别为

p1(t) =us(t)ua(t)

=k3V1I1[sin(2ωt+φ+π)+sinφ]

(23)

=k3V1I1[cos(2ωt+φ+π)-cosφ]

(24)

通过电压内积运算，得出两电压内积在永久性故障下分别近似为

(25)

(26)

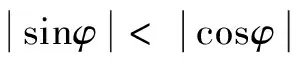
同理，P1(t)与P2(t)可通过故障相端电压与其一阶导数电压相量在健全相电压和相量上的投影得到，其结果如图5所示，从图中同样可得P1(t)幅值小于P2(t)幅值。

图5 永久性故障下电压相量图Fig.5 Voltage phase diagram under permanent fault

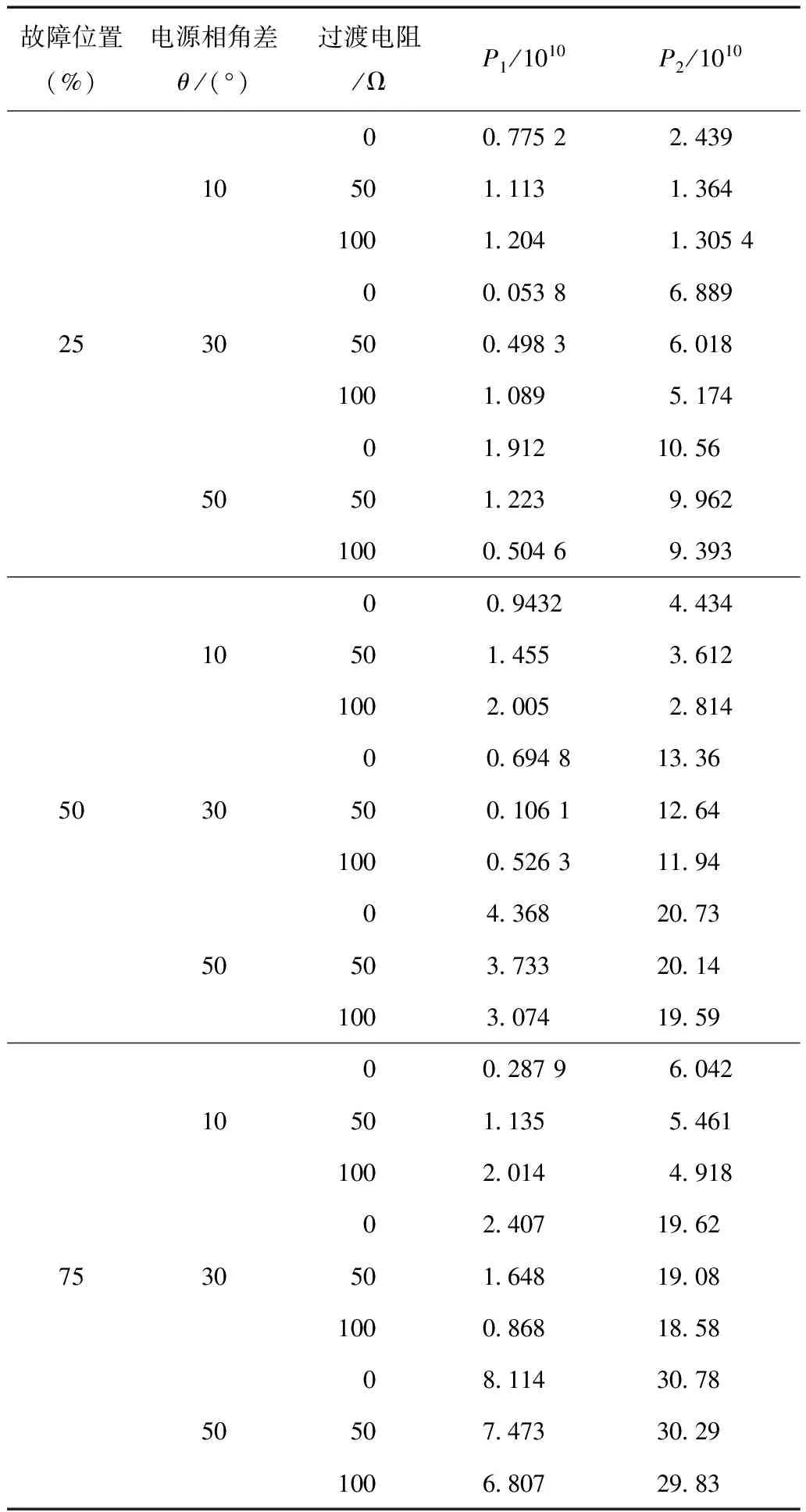
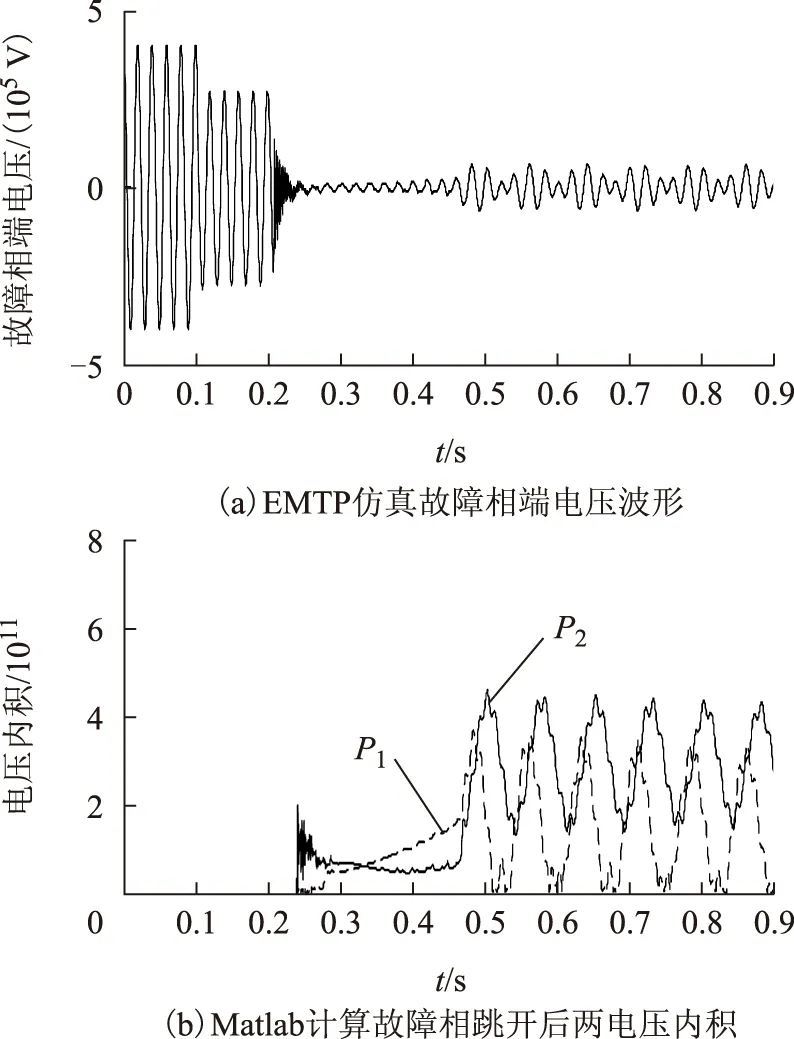
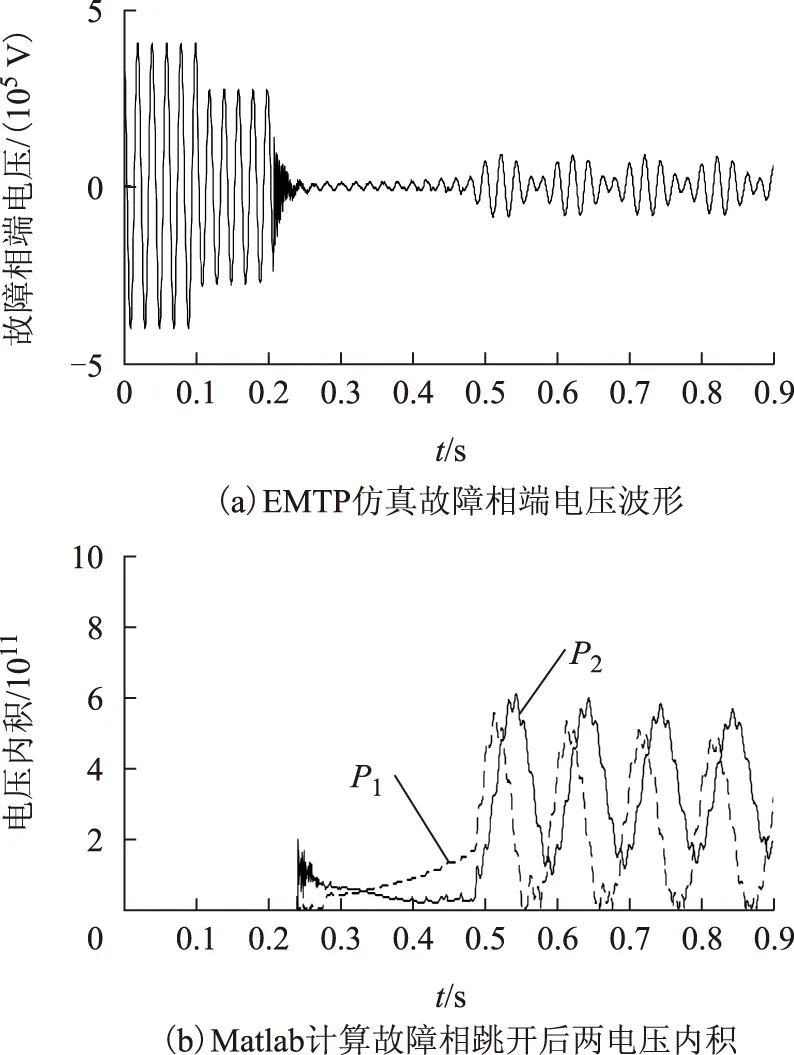
综上所述，对于瞬时性故障，在二次电弧初始阶段，内积P1(t)小于内积P2(t)；随着电弧阻值增加，P1(t)增加，P2(t)减小，两内积输出量曲线出现交点；在恢复电压阶段，P1(t)与P2(t)近似为低频正弦信号且相位相差90°，两内积输出量曲线相互交错出现交点。对于永久性故障，则有P1(t)

1.4 单相自适应重合闸方案

自适应重合闸具体实现步骤如下：

1)当线路发生单相接地故障，且检测到故障相跳闸后，为躲开暂态过程，待故障相跳开两个周波后，以2 kHz的采样频率对线路侧三相电压进行采样得到采样序列ua(k)、ub(k)、uc(k)。

2)根据式(27)求出故障相端电压一阶导数电压[17]，以A相故障为例。

(27)

式中，k为当前采样点；Ts为两个采样点之间的时间间隔。

3)选取数据窗长度为1个周波，每次滑动一个采样点得到最新数据窗的采样数据。通过式(28)、式(29)分别计算健全相电压和与故障相端电压及其一阶导数电压的内积。

(28)

(29)

式中，N为一个工频周期内的采样点数，N=40。

4)当连续5次检测到P1(k)>P2(k)，则判定故障为瞬时性。继续检测到P1(k)

5)如果在传统重合闸固有的整定重合时间内一直检测到P1(k)

2 仿真分析及方法验证

2.1 EMTP仿真验证

采用ATP-EMTP对图6所示长度为320 km的带并联电抗器的500 kV输电线路进行仿真实验。其中电源功角差δ=20°，系统阻抗：Zm1=2+j40.19 Ω，Zm0=1+j20.09 Ω；Zn1=0.5+j10.05 Ω，Zn0=1+j20.96 Ω。线路参数：R1=0.017 8 Ω/km，R0=0.175 4 Ω/km；L1=0.907 5 mH/km，L0=2.106 mH/km；C1=0.013 3 μF/km，C0=0.010 1 μF/km。两端并联电抗器每相使用XL=6 808 mH的电感与10 Ω电阻串联达到线路70%补偿，中性点选取XN=2 269 mH的电感为与10 Ω 电阻串联。电弧模型使用EMTP中TACS模块Type91，初始电弧参数：u0=12 V/cm，τ=1.3ms，l0= 400 cm，r=1.3 mΩ/km[1]。

图6 带并联电抗器输电系统仿真图Fig.6 Transmission system with shunt reactors

在线路50%处进行永久性单相接地故障仿真，接地电阻为50 Ω。图7a给出故障相端电压波形，可看出其在断路器断开后迅速衰减为幅值很小的工频电压。图7b为电压内积输出量，电压内积P1与P2经短暂态后都迅速稳定不变，且P1总小于P2。

图7 永久性故障下的仿真结果Fig.7 Results for simulation under permanent fault

为了考察故障位置、过渡电阻及电源功角差对故障性质判别的影响，表1给出了不同故障条件下的仿真结果，其中故障位置为故障点距送电端M占全线路的百分比。从表中可看出通过比较电压内积P1与P2的大小，就可以可靠识别永久性故障。

图8a、图9a、图10a分别给出了线路补偿度为60%、70%、80%时瞬时性故障下故障相端电压仿真

表1 不同条件下永久性故障仿真结果

波形。从图中可看出，故障相端电压在电弧阶段呈方波，且幅值随着时间不断增加；在恢复电压阶段，故障相端电压呈现拍频特性。图8b、图9b、图10b分别为电压内积输出量。从图可知两电压内积在二次电弧阶段有P1

图8 60%补偿线路瞬时性故障的仿真结果Fig.8 Results for simulation under transient fault with 60% line compensation levels

图9 70%补偿线路瞬时性故障的仿真结果Fig.9 Results for simulation under transient fault with 70% line compensation levels

图10 80%补偿线路瞬时性故障的仿真结果Fig.10 Results for simulation under transient fault with 80% line compensation levels

因此本文方法仅靠两内积曲线的交点就可确定瞬时性故障是否熄弧，不需整定。

上述仿真结果与理论分析一致。

2.2 变电站故障录波数据验证

采用某500 kV变电站的故障录波数据，对本文方案的工程实用性进行了验证。该变电站中船苏Ⅰ线发生A相接地故障，并触发故障录波器。图11为根据录波数据反演三相电压波形。

图11 带并联电抗器输电线路瞬时性故障录波图Fig.11 Records showing a transient fault for transmission line with shunt reactors

图12a给出了故障相端电压部分相应细节波形。图中，故障发生在相对零点时刻，45.5 ms后断路器单相跳闸进入二次电弧阶段，124.5 ms后故障电弧熄灭进入恢复电压阶段。因此，此次该带并联电抗器线路故障属于瞬时性故障，并于故障发生956.5 ms后重合闸成功。由于该线路实际采用固定时间重合闸，不能判断电弧熄弧，因而增加了线路非全相运行时间。

图12 不同自适应重合闸方案比较Fig.12 Compare with different approach for adaptive single-pole auto-reclose

图12b为本文方法的电压内积曲线。图中，在未熄弧阶段，内积P1小于内积P2，两内积曲线没有交点，这与仿真情况有一定出入。这是因为仿真给出的是理论最慢熄弧时间，而实际熄弧受多外界因素的影响，在此次故障中，电弧熄灭比理论时间提前，P1与P2没有相应的增减，因此没有出现交点。但在恢复电压阶段，P1逐渐增加并在熄弧后50 ms时刻大于P2，出现第一个交点，此时可判断为瞬时性故障；然后在约第一个拍频周期处出现第二个交点，此时可判别故障熄弧，发出重合闸命令。在此次故障中，判别熄弧时间比理论上多出约半个拍频周期，但可保证在瞬时性故障恢复电压阶段发出重合闸命令，缩短线路非全相运行时间。

图12c为根据文献[18]所提相位判据处理后的相应相位输出β。从图中可以看出，由于熄弧后电压呈现拍频特性，因而使用相位判据方法的输出量波动较大，且存在相位跃变点，不利于相位保护判据的整定。

3 结论

1)针对带并联电抗器输电线路，本文基于健全相电压和与故障相电压及其一阶导数电压求得两个电压内积，通过两电压内积曲线的交点实现自适应判别故障性质和捕捉熄弧时间，不需要整定，不受线路运行条件的影响。

2)该重合闸方案适用于二次电弧和恢复电压阶段，在故障相跳开后即可启动重合闸判据，不受二次电弧熄灭时间长短的制约；且判别瞬时性故障熄弧的准确性与二次电弧是否提前熄灭无关。

3)该方法采用时域计算方法，不需要进行频域求解，计算量非常小，不受低频振荡分量的影响。对采样频率要求不高，实施简便，能在现有的微机保护装置硬件配置下推广该技术的工程应用。

[1] 梁振锋，索南加乐，宋国兵，等.输电线路自适应重合闸研究综述[J].电力系统保护与控制，2013，41(6)：140-147. Liang Zhenfeng，Suonan Jiale，Song Guobing，et al.Research review of adaptive reclosure in transmission lines[J].Power System Protection and Control，2013，41(6)：140-147.

[2] Johns A T，Aggarwal R K，Song Y H.Improved techniques for modeling fault arcs on faulted EHV transmission systems[J].IEE Proceedings-Generation，Transmission and Distribution，1994，141(2)：148-154.

[3] Radojevic Z M，Shin J.New digital algorithm for adaptive reclosing based on the calculation of the faulted phase voltage total harmonic distortion factor[J].IEEE Transactions on Power Delivery，2007，22(1)：37-41.

[4] Radojevic Z，Terzija V，Preston G A，et al.Smart overhead lines autoreclosure algorithm based on detailed fault analysis[J].IEEE Transactions on Smart Grid，2013，4(4)：1829-1838.

[5] Djuric M B，Terzija V V.A new approach to the arcing faults detection for fast autoreclosure in transmission systems[J].IEEE Transactions on Power Delivery，1995，10(4)：1793-1798.

[6] Lin Xiangning，Weng Hanli，Liu Haifeng，et al.A novel adaptive single-phase reclosure scheme using dual-window transient energy ratio and mathematical morphology[J].IEEE Transactions on Power Delivery，2006，21(4)：1871-1877.

[7] Karacasu O，Hocaoglu M H.An adaline based arcing fault detection algorithm for single-pole autoreclosers[J].Electric Power Systems Research，2011，81(2)：367-376.

[8] 李斌，李永丽，盛鹍，等.并联电抗器的超高压输电线单相自适应重合闸研究[J].中国电机工程学报，2004，24(5)：52-56. Li Bin，Li Yongli，Sheng Kun，et al.The study on single-pole adaptive reclosure of EHV transmission lines with the shunt reactor[J].Proceedings of the CSEE，2004，24(5)：52-56.

[9] 陆岩，郑玉平，沈军，等.超高压有并联电抗器线路无故障重合闸研究[J].电力系统自动化，2008，32(6)：76-80. Lu Yan，Zheng Yuping，Shen Jun，et al.Research on adaptive reclosure of EHV transmission lines with shunt reactors [J].Proceedings of the CSEE，2008，32(6)：76-80.

[10]索南加乐，孙丹丹，付伟，等.带并联电抗器输电线路单相自动重合闸永久故障的识别原理研究[J].中国电机工程学报，2006，26(11)：75-81. Suonan Jiale，Sun Dandan，Fu Wei，et al.Identifica-tion of permanent faults for single-phase auto-reclosure on transmission lines with shunt reactors [J].Proceedings of the CSEE，2006，26(11)：75-81.

[11]索南加乐，邵文权，宋国兵，等.带并联电抗器输电线路单相自动重合闸永久性故障的识别新方法[J].中国电机工程学报，2008，28(28)：80-85. Suonan Jiale，Shao Wenquan，Song Guobing，et al.A new method to identify permanent faults for transmission lines with shunt reactors [J].Proceedings of the CSEE，2008，28(28)：80-85.

[12]索南加乐，邵文权，宋国兵.基于参数识别的单相自适应重合闸研究[J].中国电机工程学报，2009，29(1)：48-54. Suonan Jiale，Shao Wenquan，Song Guobing.Study on single-phase adaptive reclosure scheme based on parameter identification[J].Proceedings of the CSEE，2009，29(1)：48-54.

[13]刘浩芳，王增平，刘俊岭.带并补的超高压输电线单相自适应重合闸新判据[J].电力系统自动化，2007，31(24)：62-66. Liu Haofang，Wang Zengping，Liu Junling.A new criterion for single-phase adaptive reclosure of shunt reactor compensated EHV transmission lines[J].Automation of Electric Power Systems，2007，31(24)：62-66.

[14]曹芬，何奔腾.带并联电抗器的超高压输电线路单相自适应重合闸新算法[J].电力系统自动化，2009，33(23)：55-60. Cao Fen，He Benteng.New algorithm for single-phase adaptive reclosure for EHV transmission lines with shunt reactor compensated[J].Automation of Electric Power Systems，2009，33(23)：55-60.

[15]索南加乐，梁振锋，宋国兵.自适应熄弧时刻的单相自适应重合闸研究[J].电力系统保护与控制，2012，40(5)：37-41. Suonan Jiale，Liang Zhenfeng，Song Guobing.Study of single-phase reclosure with adaptive secondary arc extinction[J].Power System Protection and Control，2012，40(5)：37-41.

[16]Zadeh M R D，Kanabar I V M，Xue Y.An adaptive HV transmission lines reclosing based on voltage pattern in the complex plane[C]//Conference for Protective Relay Engineers，College Station，TX，2012：2-5.

[17]Eissa M M.Development and investigation of a new high-speed direction relay using field data[J].IEEE Transactions on Power Delivery，2008，23(3)：1302-1309.

[18]李斌，李永丽，黄强，等.单相自适应重合闸相位判据的研究[J].电力系统自动化，2003，27(22)：41-44. Li Bin，Li Yongli，Huang Qiang，et al.Study on phase criterion for single-phase adaptive reclosure[J].Automation of Electric Power Systems，2003，27(22)：41-44.

(编辑 赫蕾)

A Voltage Inner Product Based Approach for Single-Phase Adaptive Reclosure on Transmission Line with Shunt Reactors

LuoXunhua1HuangChun1JiangYaqun1TangTao1ChenHong2

(1.College of Electrical Engineering & Information Technology Hunan University Changsha 410082 China 2.Hunan Electric Power Company of Scientific Research Changsha 410007 China)

In this paper, a single phase adaptive reclosure method for high voltage (HV) transmission lines with shunt reactors which based on inner products of voltage is proposed. Healthy phases voltage and fault phase voltage inner product are treated as initialization inner product, inner products of healthy phase voltage and derivative of fault phase voltage as compensation inner product when single-phase grounding fault appear and the fault phase ends of circuit breaker tripping. To permanent fault, the initialization inner product will keep smaller than compensation inner product in a short transient state, therefore, two inner product curve won't appear intersection. As for transient fault, in the second arc initial stage, the initialization inner product is smaller than the compensation inner product; with the increase of arc resistance, the initialization inner product increase while the compensation inner product decrease, they would have a point of intersection. After arc extinction, low-frequency oscillation is observed in two curves of voltage inner products which have 90° phase differences; they would also have points of intersection. According to this phenomenon, the point of intersection of voltage inner products are used to identify permanent and transient faults and to determine the transient fault has entered the stage of recovery voltage when the second intersection appears. The proposed algorithm needs no threshold which can easily operate and start when the circuit breaker single-phase tripping appears. It does not need to be calculated in frequency domain and not affected by low frequency oscillation component. The EMTP simulations and field data verified its correctness and effectiveness.

Transmission line，adaptive reclosing，fault arc，inner product

国家自然科学基金(51677060)和国家电网公司研究开发项目(5216A313500N)资助。

2016-05-29 改稿日期2016-10-31

TM77

罗勋华 男，1989年生，博士研究生，研究方向为电力系统继电保护、电气信号处理。

E-mail：luoxunhuas@163.com

黄 纯 男，1966年生，教授，博士生导师，研究方向为电力系统保护与控制、电能质量分析与控制、信号处理。

E-mail：yellowpure@21cn.com(通信作者)