考虑定子外壳漏磁的同极式永磁偏置径向磁轴承磁路模型

吴磊涛 王 东 苏振中 张贤彪 王 抗

(海军工程大学舰船综合电力技术国防科技重点实验室 武汉 430033)



考虑定子外壳漏磁的同极式永磁偏置径向磁轴承磁路模型

吴磊涛 王 东 苏振中 张贤彪 王 抗

(海军工程大学舰船综合电力技术国防科技重点实验室 武汉 430033)

同极式永磁偏置径向磁轴承的永磁偏置磁场在定子外壳内形成较大漏磁，而且外壳的有效面积相对工作气隙较大，即使在铁心与外壳间加入隔磁层的情况下，漏磁仍不可忽略，必须进行准确计算。首先直接求解拉普拉斯方程获得隔磁层内的磁场分布，并结合保角变换计算漏磁区域的端部效应，然后求解工作气隙的永磁偏置磁场和电励磁控制磁场，最后建立完整磁路模型和电磁力解析模型。三维有限元仿真结果表明，所建立的磁路模型能准确计算磁轴承工作范围的电磁参数。依据飞轮储能系统的总体需求，设计了径向磁轴承系统，实验结果验证了所建立解析模型和有限元模型的准确性。

磁轴承 解析模型 漏磁 磁路模型 线性模型

0 引言

永磁偏置混合磁轴承(下文称混合磁轴承)由于其固有的无接触摩擦和刚度、阻尼可控的特性，广泛应用于各种高速转子系统[1-3]。与纯电励磁轴承相比，混合磁轴承的励磁功耗和旋转损耗低，且结构更紧凑[4]；与纯永磁轴承相比，其承载力更大，且具有独立实现五自由度稳定悬浮转子的能力[5]。

同极式永磁偏置磁轴承(下文称同极式磁轴承)是径向混合磁轴承的一种，其旋转损耗低[6]，永磁体与定子铁心相对独立，便于安装[7]，因此适用于飞轮储能、卫星动量轮等系统[8，9]。同极式磁轴承本身存在电磁机构固有的结构缺点，漏磁不可避免[10]。其漏磁分为电励磁漏磁和永磁漏磁两大类。电励磁漏磁主要是在线圈槽内漏磁，影响较小[11]；由于永磁体不导磁，磁阻在磁路中比重较大，永磁漏磁的影响不可忽略[12]。

目前国内外学者对磁轴承的精确设计方法展开了深入研究，但漏磁与磁阻在设计时通常被忽略[13，14]或只通过磁路法与经验值确定[15]，设计精度不高。为了提高对漏磁的计算精度，有限元仿真被引入漏磁场计算[16]，但耗时较长，不适用于快速的电磁设计。解析法是研究磁轴承磁场分布的重要方法[17，18]，但在漏磁场计算中应用较少。

在实际生产中，为了保证产品安全，同时降低成本，不可避免地选用高强度的导磁钢作为系统外壳，即使隔磁层将磁轴承定子与外壳分离，二者之间存在较大的漏磁，必须进行准确计算确定其影响。

本文通过傅里叶级数法和保角变换法联合求解漏磁区域的磁场分布，然后求解永磁偏置气隙磁场和电励磁控制气隙磁场，结合电机无齿槽效应的偏心模型建立了精确磁路模型和电磁力解析模型。设计并制造了径向磁轴承及其控制系统，实验验证了所建立的解析模型和有限元模型的准确性。

1 同极式磁轴承的结构和原理

同极式磁轴承的转子铁心通过热套固定在转轴上，转轴材质为导磁材质的合金钢，导磁环在两个转子铁心(硅钢叠片结构)之间，起辅助导磁和定位铁心的作用。

定子结构包含两个叠片铁心，每个铁心上有4个磁极，每个磁极上均绕置了一个集中绕组，各绕组的尺寸和匝数相同。叠片铁心的外侧热套有实心的导磁环，材料为电工纯铁，两个导磁环之间放置轴向充磁的钕铁硼永磁环。在导磁外壳和定子铁心之间嵌入隔磁铜套以固定定子、外壳并隔绝永磁体漏磁，整个永磁磁场的漏磁主要集中在此。

径向磁轴承包含两个定子铁心和两个转子铁心，因此，径向磁轴承包含两组工作气隙。永磁体所产生的磁通将沿着轴向磁路流通，依次经过导磁环、定子铁心、转子铁心和转轴形成闭合回路。

当转子处在平衡位置时，由于结构对称，各气隙内的磁感应强度相等，电磁力合力为0。当转子偏离平衡位置时，控制绕组内的电流将根据转子偏心方向和位移在气隙内产生电励磁磁通，从而增强或减弱气隙内的磁感应强度，进而产生电磁力，使转子回到平衡位置。

2 同极式磁轴承的解析模型

2.1 漏磁场模型

本文采用解析法求解定子和导磁外壳之间的漏磁场，同时结合漏磁场结果计算气隙磁场，为了便于分析，解析模型的假设如下：

1)定、转子铁心及外壳的磁导率无穷大。

2)隔磁铜套、永磁体的相对磁导率μr=1。

3)忽略转子铁心的涡流效应。

4)忽略磁极极靴。

隔磁层与导磁外壳之间的漏磁区域在同极式磁轴承结构中的位置如图1 所示，漏磁模型示意图如图2所示。

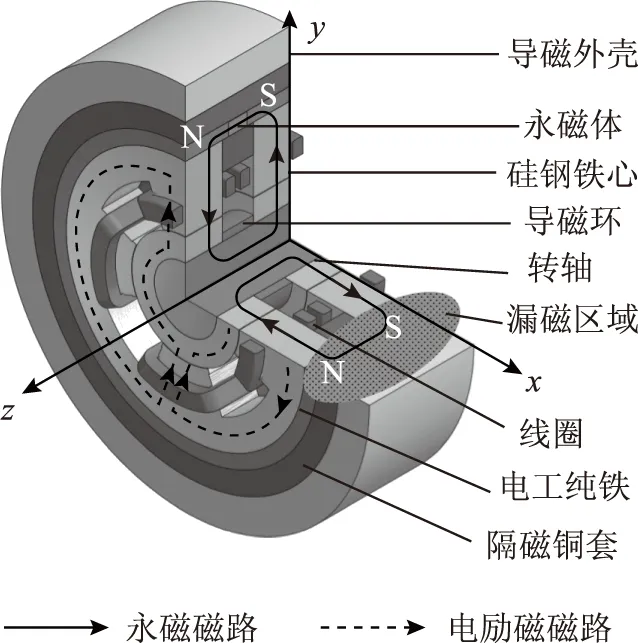
图1 同极式磁轴承结构示意图Fig.1 The structure of homopolar magnetic bearing

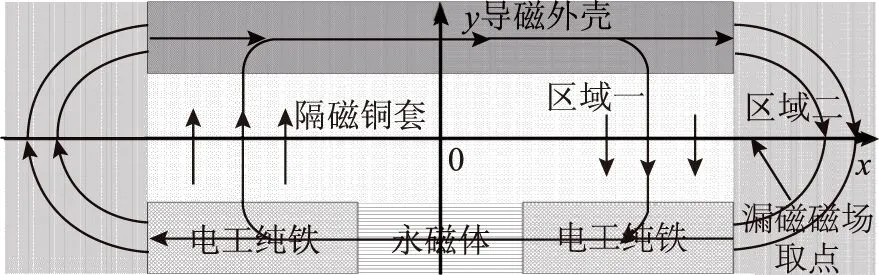
图2 漏磁场的模型示意图Fig.2 Structure model of the leakage field

求解区域分为隔磁铜套(区域一)和端部空气(区域二)两部分，分别采用傅里叶变换法和保角变换法求解磁场，然后线性叠加。

隔磁铜套内的漏磁场是由各个边界条件共同决定，且标量磁位场在永磁体和边界的空气内是线性分布，对此分别计算各个边界磁位函数对磁场造成的影响，最终求解出隔磁层内的磁场分布，如图3所示。图3中，a为磁极的厚度，b为1/2永磁体厚度，g为隔磁铜套的厚度。

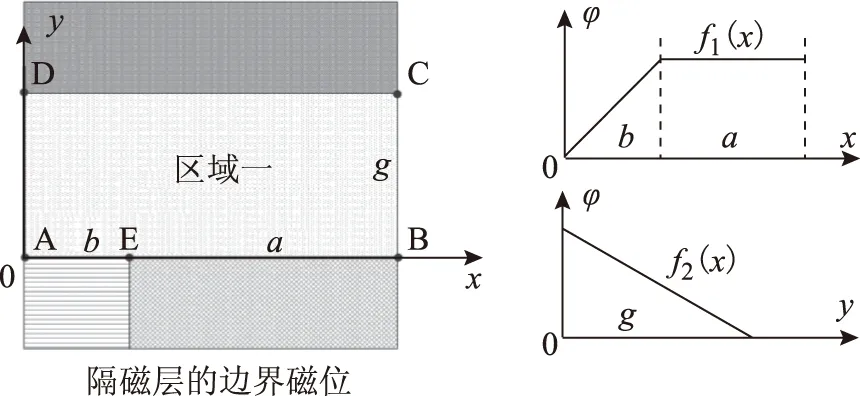
图3 隔磁层的漏磁场及其边界磁位示意图Fig.3 The leakage field of copper area and its magnetic potential in boundary

磁场由各个边界条件共同决定，分别计算各个边界磁位对磁场造成的影响，并线性叠加。因此，隔磁层内的磁位函数u(x，y)表达为

u(x,y)=W(x,y)+V(x,y)

(1)

式中，W(x，y)、V(x，y)分别为边界AB、BC对隔磁层内磁场产生的磁位函数。

对于W(x，y)，首先用分离变量法求解直角坐标下的方程

[gmsinh(my)+hmcosh(my)]

(2)

按照表1所示，各边界上的磁位函数方程为

(3)

表1 隔磁层内漏磁场的边界条件

依据式(3)给出的边界条件，将式(2)整理为

(4)

在AB边界，有

(5)

将边界磁位函数f1(x)展开，从而可以求解出式(5) 中的系数，即

cos[m(a+b)]+msin(mb)}

(6)

根据表1，同理可得

(7)

其中

(8)

根据磁位函数u(x,y)可得隔磁层内的磁场密度的y向分量为

(9)

为了准确获得漏磁场的完整分布，必须考虑磁场的边缘效应，如图4a所示。由于该磁场的边界是不等磁位，必须通过两次许-克变换。

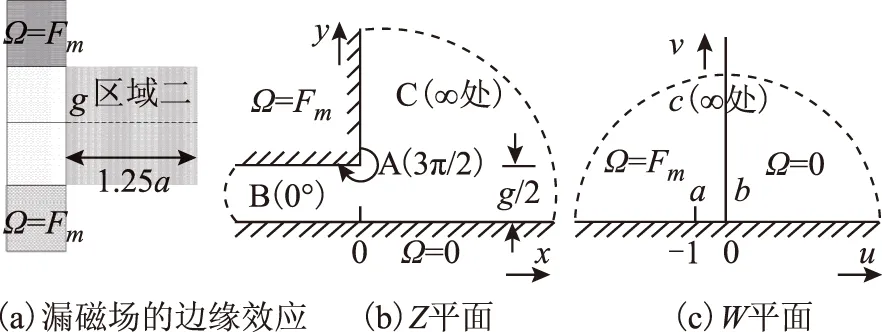
图4 漏磁场的边缘效应求解示意图Fig.4 The fringe effect of leakage field and its solution

图4a中，设定导磁外壳的磁位为Fm，电工纯铁层的磁位为-Fm，则气隙中心线的磁位可视为0，据此可转换为图4b。

根据图4b，第一次许-克变换为

(10)

式中，S的值可由回路积分法确定。

在Z平面内，经过B点时，积分距离为g/2，则

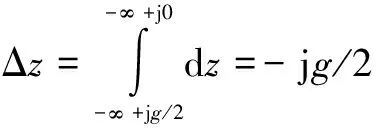
(11)

在W平面内，在b点内做半径趋于无穷小的半圆，令w=ρejθ，ρ→0，θ从π积分到0，则

(12)

结合式(11)、式(12)可得

(13)

通过对数变换获得原求解区域与规则区域之间的关系为

(14)

求解区域内的磁感应强度为

(15)

根据式(15)，当z→-∞时，w→0，磁感应强度Ba最大，即Bmax=μ0(2Fm)/g。选取不同的w值代入式(15)，可得边缘处的磁场分布。

将式(9)和式(15)置于同一坐标系下，可推导出整个漏磁场的分布。

2.2 气隙磁场模型

如图5所示，为了简化计算，假设如下：

1)定子磁极无极靴，转子表面光滑。

2)相对气隙的大小，槽深为无限深，槽高为无限高。

3)铁心的磁导率为无穷大，忽略涡流和磁滞。

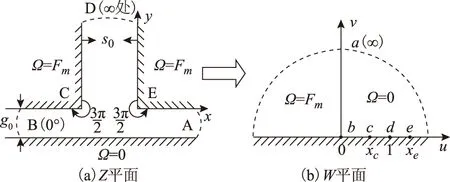
图5 气隙磁场求解示意图Fig.5 The magnetic field of air-gap field and its solution

偏置磁场中相邻磁极的磁位相同，但定、转子的磁位不同，因此同样需进行两次许-克变换。

根据图5b，许-克变换为

(16)

积分并分别在A、B、C、E点利用回路积分法求解未知数，最后可以得到

(17)

其中

(18)

式中，s0为磁极之间的宽度。

结合对数变换

(19)

可得工作气隙内的磁感应强度为

(20)

根据图5b，当w为不同负实数时，分别求解Ba和对应的z值，可得转子表面的磁感应强度分布。

2.3 转子偏心模型

转子偏离平衡位置时，磁轴承的工作气隙的改变导致磁阻变化，磁场分布规律随之改变。气隙内的磁力线长度与齿槽无关，因此假定偏心分析模型为无齿槽结构，如图6所示[19]。

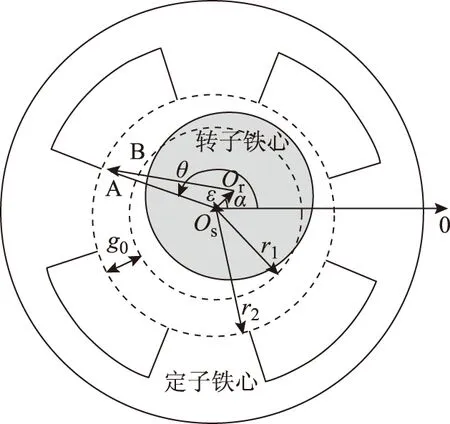
图 6 转子偏心示意图Fig.6 Model of the rotor eccentricity

设转子中心偏移定子中心的距离为ε，偏移角度为α，设定子内圆任一点A与偏心后的转子中心的连线经过转子外圆上的B点。为了将偏心模型嵌入齿槽模型，计算偏心后气隙长度AB函数[19]

g(θ)=g0-εcos(θ-α)

(21)

假定转子偏心前后定、转子之间的磁位压降不变，以此为依据可以得到转子偏心前后磁感应强度之间的关系为

(22)

式中，g0、B0分别为平衡位置的工作气隙大小和气隙磁感应强度。

2.4 磁路和电磁力模型

假定定、转子铁心均未饱和，因此，转轴、导磁环的导磁率恒定；定子铁心的轴向漏磁阻相对气隙磁阻较大，对磁路结果影响较小，因此，采用等效磁阻法计算以上部件的磁阻。根据2.1节、2.2节的分析结果，可得各气隙在平衡、偏心状态的等效磁阻R1x、R2x以及定子铁心与外壳间的漏磁阻Rσ1、Rσ2，建立完整磁路模型，如图7所示。

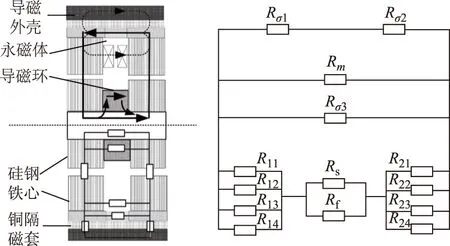
图7 同极式磁轴承的磁路模型Fig.7 The magnetic circuit model of homopolar magnetic bearing

图7中，R1x、R2x为工作气隙等效磁阻，x=1、2、3、4，Rσ1、Rσ2为定子铁心与外壳之间的漏磁阻，Rσ3为定子轴向之间的漏磁阻，Rf、Rs分别为转轴、导磁环的等效磁阻。

定义漏磁系数为

(23)

式中，Φall为磁路总磁通；Φg为气隙磁通(有效磁通)。

根据图7，存在关系

Φall=Φg+Φσ1,2+Φσ3

(24)

其中，根据2.1节、2.2节的解析结果可得

Φg=∫BgdS

(25)

Φσ1,2=∫Bσ1,2dS

(26)

由于Φσ3对应的漏磁阻形状相对规则，可采用等效磁路法计算。

同极式径向磁轴承含有两个独立的定子铁心，每个铁心有相同的4个磁极，其电磁力可以归算到两个相互垂直的方向上，如图1所示，x轴为水平，y轴为垂直。以水平方向为例，转子铁心在磁场中受到的力为

(27)

基于所建立的磁场解析模型和磁路模型获得的气隙磁场分布是离散的，对此采用数值计算转子铁心受到的电磁力为

(28)

式中，n为转子外圆上取点数目；θi为θ在第i个点对应的角度大小。

3 有限元模型与解析模型对比

3.1 漏磁场

从图2漏磁气隙中点线位置取点，设定图2的0点 和x轴对应漏磁磁感应强度的起点、横轴，可得漏磁场在轴向的分布结果，如图8所示。

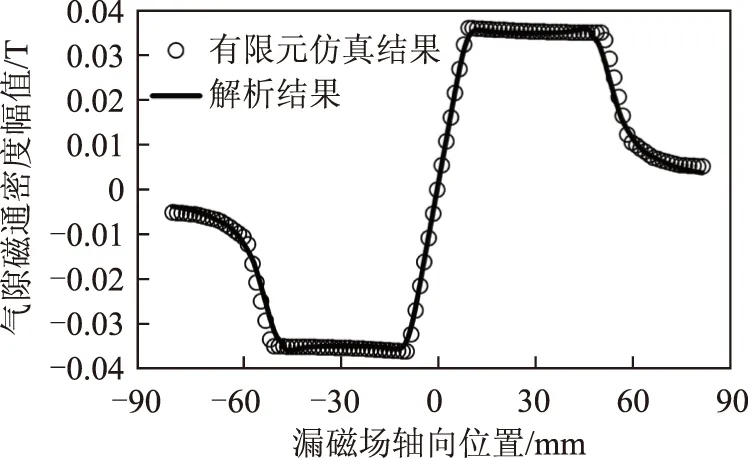
图8 漏磁场的径向分量在轴向的分布Fig.8 The radial component of leakage field in axial position

由图8可知，解析模型和有限元仿真结果吻合较好,二者之间仅在磁极边缘位置存在一定的偏差，主要是由于有限元模型在导磁区域的边缘出现少量趋肤效应所致。

计算漏磁系数与铜套厚度的关系，并与有限元仿真对比，如图9所示。

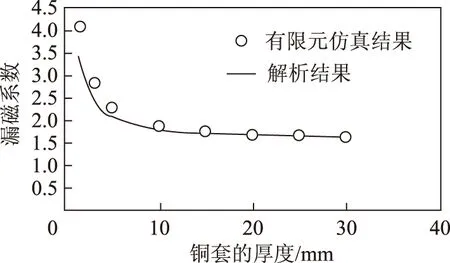
图 9 漏磁系数与铜套厚度的关系Fig.9 The relationship between the leakage coefficient and the thickness of copper

由图9可知，漏磁系数在铜套厚度大于5mm后快速减小，大于10mm后趋于平稳，说明铜套的厚度应大于5mm；铜套小于5mm后的解析解与有限元解的差别变大，主要是解析法假设导磁外壳的磁导率无穷大，而实际上导磁外壳是普通钢，相对磁导率在300～500之间，当铜套很薄时，外壳磁阻不可忽略。

在外壳不导磁(即铜套无穷厚)的情况下，解析和有限元求得的漏磁系数约为1.5，说明Rσ3及其他位置的漏磁也不可忽略。结合图9，当铜套的厚度大于10 mm 时，漏磁系数为1.9，说明由导磁外壳导致的漏磁不再占主导，因此铜套的厚度设置为10 mm。

3.2 气隙磁场

设定图6中0点位置为工作气隙磁通密度的0点，横坐标为工作气隙的中心线，图11、图12与之定义相同。永磁偏置气隙磁场分布如图10所示。

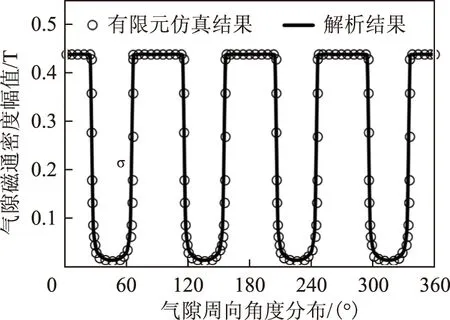
图 10 永磁偏置气隙磁场分布Fig.10 The flux density distribution of PM biased field

由图10可知，采用保角变换的解析解与有限元解较吻合，仅在空间上存在轻微的错位，这与保角变换本身有关。在实际取Bmax时，取w是一个较大的有限值，而不是无穷大，无法精确获得Bmax与z的关系。

混合励磁磁轴承的气隙磁场由永磁偏置磁场和电励磁控制磁场两部分组成。进行电磁设计时一般保证避免铁心饱和的情况出现，因此气隙磁场解析结果可以由两种励磁形式的磁场解析结果线性叠加。由于电励磁磁场的求解过程近似于偏置磁场，解析解和有限元解对比如图11所示。

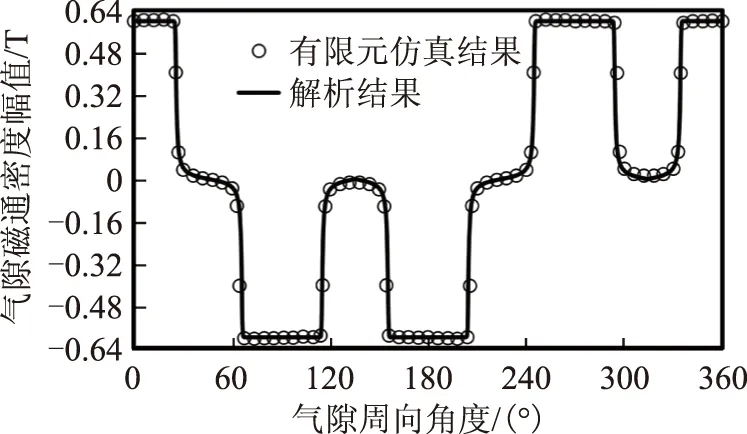
图 11 电励磁气隙磁场分布Fig.11 The flux density distribution of electro-magnetic field

3.3 转子偏心后的气隙磁场

结合同极式磁轴承运行的实际情况，设置转子偏心值为0.25 mm,根据磁轴承在x、y轴的对称性，0°和45°是其偏心角度的边界，计算两种情况的气隙磁场分布，并与有限元仿真结果对比，如图12所示。

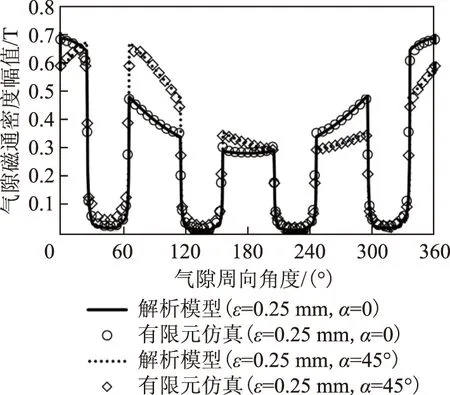
图12 转子偏心状态的气隙偏置磁场分布Fig.12 The PM biased field of air gap with eccentricity

4 同极式磁轴承样机实验

4.1 磁轴承样机

为了保证电磁力与转子位移和控制电流之间具有较好的线性特性，定、转子铁心在整个工作区间内应不发生饱和，最大磁感应强度取1.2 T，偏置磁通与最大磁通的比例设定为0.5，但由于定子铁心与外壳之间存在漏磁场，实际的磁感应强度最大为1.05 T，偏置磁通与最大磁通的比值为0.43。表2给出了永磁偏置径向磁轴承的电磁设计结果。

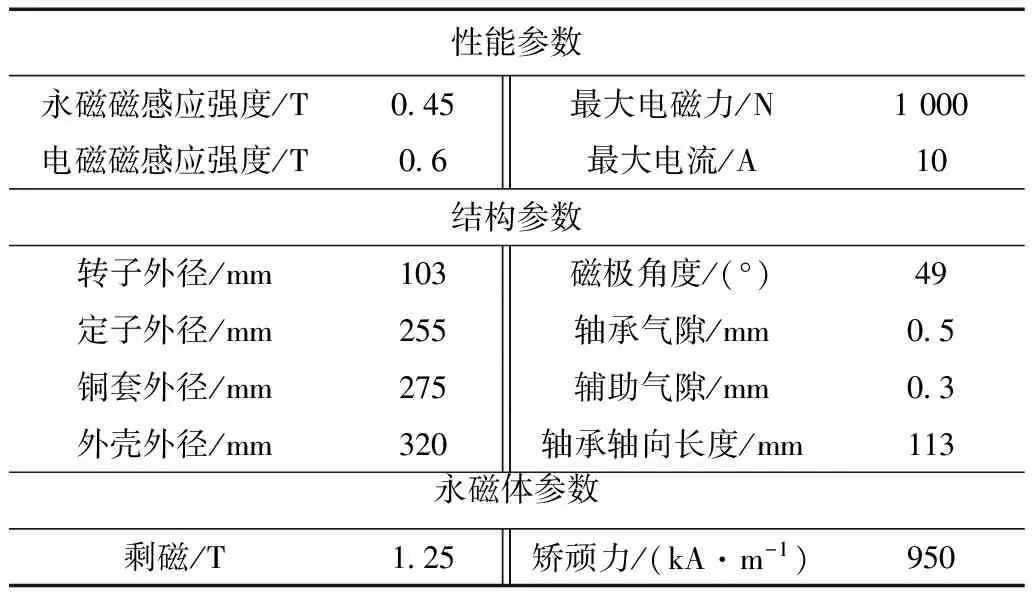
表2 径向磁轴承的电磁参数

同极式永磁偏置径向磁轴承样机如图13所示。

图13 同极式径向磁轴承样机Fig.13 The prototype of radial magnetic bearing

4.2 磁轴承刚度实验

本文搭建了百公斤级立式飞轮储能转子-支承系统以便进行径向磁轴承的相关实验并验证提出的解析模型。完整的转子-支承系统为五自由度磁悬浮支承，包括两个径向磁轴承和一个轴向磁轴承，系统结构如图14 所示。

图14 飞轮储能转子-支承系统实物图Fig.14 The physical map of the flywheel rotor-support system

由于工作气隙和隔磁层内的磁感应强度难以直接测量，只能间接测量转子位移、控制电流和电磁力，因此通过实验的方法测量磁轴承的电流刚度和位移刚度，并与解析解、有限元解对比。

测量电流-电磁力关系时，将力传感器的信号取出，与电流信号一并输入控制器，由于二者的信号是同步采集，因此可以直接或者借助器械施力到转子上。力的方向需要保持水平，且与图1磁轴承的x或y方向保持一致。施力位置为转子上、下的两个端部，获得两个力矩方程后解方程即可。

电流刚度的测试结果如图15所示。

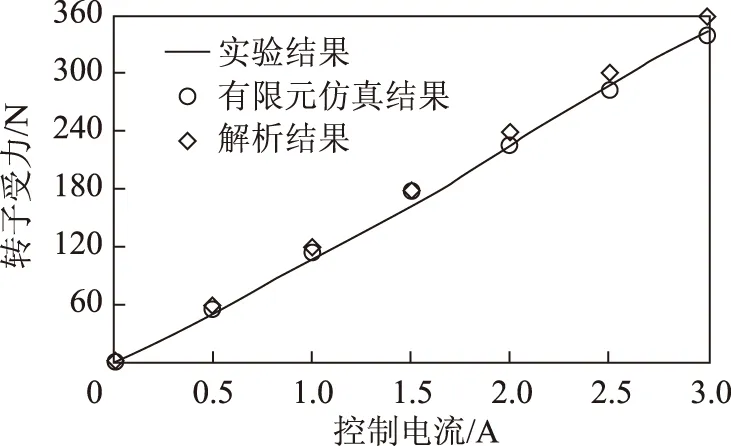
图15 电磁力与控制电流之间的关系Fig.15 The relationship between the magnetic force and current

由图15可知，实验结果与解析模型、有限元仿真吻合较好，误差在5%以内，说明电流刚度的计算模型、实验方法正确。由于装配工艺等因素造成的偏差，测量值略小于解析值。

利用控制系统使得转子偏离中心位置，为了维持转子的稳定悬浮状态，控制系统将产生相应的电流。通过测试控制电流与转子位移之间的关系，间接计算位移刚度。

径向磁轴承转子偏心平衡位置与控制电流之间的关系如图16所示。

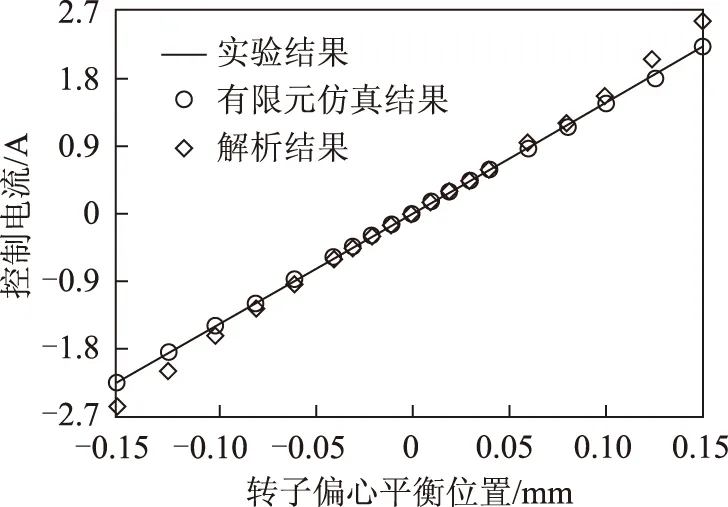
图16 转子偏心平衡位置与控制电流的关系Fig.16 The relationship between the eccentric position and control current

由图16可知，实验结果与解析解吻合的较好，证明了径向磁轴承模型准确；解析模型在位移较大位置计算的控制电流相对于实验、有限元结果偏大，这主要是由于解析模型中设置铁心磁导率为无穷大，但实验、有限元模型中铁心的磁导率为有限值，易在局部发生饱和。

5 结论

1)采用傅里叶级数法求解隔磁层内的磁场分布，采用保角变换法求解漏磁场的边缘效应，得到定子铁心和外壳之间的漏磁场解析模型。

2)采用保角变换求解气隙磁场，建立考虑转子偏心、定子漏磁的完整磁路模型，基于该模型采用数值计算的方法计算转子受力，建立径向磁轴承的线性数学模型。

3)建立有限元仿真模型，将有限元解与解析解对比，二者之间的误差较小。

4)对同极式径向磁轴承进行了电磁设计，搭建了样机及其控制系统，分别测量了电流刚度和位移刚度两个重要参数，与解析解和有限元解对比，验证了模型的准确性。

[1] 唐长亮，戴兴建，王健，等. 20 kW/1 kWh飞轮储能系统轴系动力学分析与试验研究[J]. 振动与冲击，2013，32(1)：38-42. Tang Changliang，Dai Xingjian，Wang Jian，et al. Shafting dynamic analysis and test for a 20 kW/l kWh flywheel energy storage system[J]. Journal of Vibration and Shock，2013，32(1)：38-42.

[2] 宗鸣，吴桐，王大朋. 高速电机用混合式径向磁轴承前馈解耦控制[J]. 电工技术学报，2015，30(14)：539-544. Zong Ming，Wu Tong，Wang Dapeng. Feed-forward compensation decoupling control for hybrid radial magnetic bearing used in high speed electric machine[J]. Transactions of China Electrotechnical Society，2015，30(14)：539-544.

[3] Su Zhenzhong，Wang Dong，Chen Junquan，et a1. Improving operational performance of magnetically suspended flywheel with PM-biased magnetic bearings using adaptive resonant controller and nonlinear compensation method[J]. IEEE Transactions on Magnetics，2016，52(7)：8300304.

[4] Fang Jiancheng，Sun Jinji，Xu Yanliang，et a1．A new structure for permanent-magnet-biased axial hybrid magnetic bearings[J]．IEEE Transactions on Magnetics，2009，45(12)：5319-5325.

[5] 张维煜，朱煌秋，袁野. 磁悬浮轴承应用发展及关键技术综述[J].电工技术学报，2015，30(12)：12-20. Zhang Weiyu，Zhu Huangqiu，Yuan Ye. Study on key technologies and applications of magnetic bearings[J]. Transactions of China Electrotechnical Society，2015，30(12)：12-20.

[6] Matsuzaki T，Takemoto M，Ogasawara S，et a1. A basic study of a novel homopolar type magnetic bearing unifying four C-shaped cores for high output and low loss[J]. IEEE Transaction on Magnetics，2015，51(11)：8114604.

[7] Ji Li，Xu Longxiang，Jin Chaowu. Research on a low power consumption six-pole heteropolar hybrid magnetic bearing[J]. IEEE Transactions on Magnetics，2013，49(8)：4918-4926.

[8] Hou Eryong，Liu Kun. A novel structure for low-loss radial hybrid magnetic bearings[J]. IEEE Transactions on Magnetics，2011，47(12)：4725-4733.

[9] Fang Jiancheng，Wang Xi，Wei Tong，et al. Homopolar 2-ploe radial permanent-magnet biased magnetic bearing with low rotating loss[J]. IEEE Transactions on Magnetics，2012，48(8)：2290-2303.

[10]董霞，刘志珍，宁大海，等. 基于传输线模型的三相变压器直流偏磁仿真分析[J]. 电力系统保护与控制2013，40(23)：11-16. Dong Xia，Liu Zhizhen，Ning Dahai，et a1. Simulation study for the three-phase transformer under DC bias based on the transmission-line model[J]. Power System Protection and Control，2013，40(23)：11-16.

[11]梅磊，张广明，王德明. 永磁偏置型径向磁悬浮轴承参数设计方法研究[J]. 机械科学与技术，2013，32(13)：1859-1860. Mei Lei，Zhang Guangming，Wang Deming. Parameter design method of permanent magnet biased radial magnetic bearing[J]. Mechanical Science and Technology for Aerospace Engineering，2013，32(13)：1859-1860.

[12]Sun Yanhua，Ho Yick-Sing，Yu Lie. Dynamic stiffnesses of active magnetic thrust bearing including eddy-current effects[J]. IEEE Transactions on Magnetics，2009，45(1)：139-149.

[13]Jin Ping，Fang Shuhua，Lin Heyun，et al. Analytical magnetic field analysis and prediction of cogging force and torque of a linear and rotary permanent magnet actuator[J]. IEEE Transactions on Magnetics，2011，47(10)：3004-3007.

[14]Wu L J，Zhu Z Q. Simplified analytical model and investigation of open-circuit AC winding loss of permanent-magnet machines[J]. IEEE Transactions on Industrial Electronics，2014，61(9)：4990-4999.

[15]Le Yun，Sun Jinji，Han Bangcheng. Modeling and design of 3-DOF magnetic bearing for high-speed motor including eddy current effects and leakage effects[J]. IEEE Transactions on Industrial Electronics，2016，63(6)：3656-3665.

[16]邱文祥，李大兴，夏革非，等. 一种新型低成本飞轮储能用永磁偏置磁轴承[J]. 电工技术学报，2015，30(1)：58-62. Qiu Wenxiang，Li Daxing，Xia Gefei，et al. A low cost permanent magnet biased bearing used in flywheel energy storage system[J]. Transactions of China Electrotechnical Society，2015，30(1)：58-62.

[17]Marth E，Jungmayr G，Amrhein W. A 2-D-based analytical method for calculating permanent magnetic ring bearings with arbitrary magnetization and its application to optimal bearing design[J]. IEEE Transactions on Magnetics，2014，50(5)：1-8.

[18]陈浈斐，夏长亮，王慧敏. 考虑齿槽效应的表贴式永磁电机空载磁场建模[J]. 电工技术学报，2014，29(5)：9-16. Chen Zhenfei，Xia Changliang，Wang Huimin. Modeling for open circuit magnetic field prediction in slotted surface-mounted permanent-magnet machine[J]. Transactions of China Electrotechnical Society，2014，29(5)：9-16.

[19]Wang Kang，Wang Dong，Shen Yang，et al. Subdomain method for permanent magnet biased homo-polar radial magnetic bearing[J].IEEE Transactions on Magnetics，2016，52(7)：1-1.

(编辑 于玲玲)

Leakage Magnetic Field and Precise Magnetic Circuit Model of the Permanent Magnetic Biased Radial Magnetic Bearing

WuLeitaoWangDongSuZhenzhongZhangXianbiaoWangKang

(National Key Laboratory of Science and Technology on Vessel Integrated Power System Naval University of Engineering Wuhan 430033 China)

The stator core of the classical permanent magnetic biased radial magnetic bearing(PMRMB)could produce magnetic flux leakage with the shell easily. Because of the larger area compared with air-gap in this location，the leakage magnetic field can′t be ignored even there is magnetism-insulator embedded in it. The paper get the flux density distribution in the stator and the shell with the Laplace equation，then the conformal transform method is applied to obtain the flux density distribution in the air-gap generated by permanent magnet and electro-magnet，the complete magnetic circuit model is established. The proposed magnetic circuit model proved to be effective to calculate the electromagnetic parameters in operation range by 3D finite element analyses(FEA). The PRMB is designed based on the demand of the flywheel energy storage system. A prototype PRMB is manufactured with its control system，and the effectiveness of the proposed magnetic circuit model and 3D FEA is validated by the test results.

Magnetic bearing，analytical model，leakage magnetic field，magnetic circuit model，linear model

国家自然科学基金项目(51137005，51407192)和国家自然科学重点基础研究发展计划(973计划)项目(2013CB035601)资助。

2016-04-12 改稿日期2016-07-12

TM315

吴磊涛 男，1988年生，博士研究生，研究方向为磁轴承基础技术。

E-mail：2008wuleitao@163.com

王 东 男，1978年生，教授，博士生导师，研究方向为电力推进、集成发电。

E-mail：wangdongl@vip.sina.com(通信作者)