基于负载位置反馈的永磁同步电机驱动柔性负载谐振抑制方法

丁有爽 肖 曦

(电力系统及大型发电设备安全控制和仿真国家重点实验室(清华大学电机系) 北京 100084)



基于负载位置反馈的永磁同步电机驱动柔性负载谐振抑制方法

丁有爽 肖 曦

(电力系统及大型发电设备安全控制和仿真国家重点实验室(清华大学电机系) 北京 100084)

柔性负载广泛存在于电气传动系统中。根据柔性的成因，伺服系统中柔性负载主要分为柔性关节和柔性连杆两类系统。针对这两类典型的柔性负载系统，首先引用已有的研究成果对其建立了一致的动力学模型。然后将PI调节器应用于系统控制中，由于自由度有限，谐振抑制效果并不理想。因而，控制系统中需要引入状态反馈。针对谐振抑制的需要，通过增加一个额外的位置传感器对末段位置进行测量，然后将其反馈至控制系统中。针对负载位置反馈策略，分析了其系统性能与参数关系，并采用三种策略对其进行了极点配置。仿真和实验验证了所提出的基于负载位置反馈及其参数整定方法的有效性。

永磁同步电机 柔性负载 负载位置反馈 极点配置

0 引言

在工业机器人、航天机构驱动等运动控制系统中，操作机构尺寸越来越大，因此通常采用结构轻、自重比高的结构材料。这些机构在运动中会产生明显的形变，并引起相应的应力，带有典型的柔性负载特征，对于大尺寸工作部件，有时也称为挠性负载特征。柔性负载特征对运动控制特性影响很大，容易引起谐振、定位不准甚至导致系统的不稳定。在高性能运动控制系统中，一般采用永磁交流伺服电机驱动工作机构，常见的模式有：①伺服电机通过柔性传动机构拖动刚性工作部件；②伺服电机直接驱动柔性工作部件。为提升此类系统的控制性能，有必要对系统进行更准确的建模，并在此基础上结合伺服电机的控制方案综合分析此类柔性负载引起的谐振等问题。

伺服系统中常见的柔性负载有传递旋转运动的齿轮箱、减速器等柔性关节，也有尺寸较大的工作部件，如工业机器人的机械臂、自动化设备中的操作连杆等。柔性部件在伺服系统运转过程中会产生一定程度的扭曲、弹性形变和剪切变形。针对柔性系统的建模及所引起的谐振等问题，许多学者进行了大量的研究。

就目前的研究状况，交流伺服系统中柔性负载谐振抑制方法主要包括被动控制方法和主动控制方法两类。被动控制方法主要包括频率陷波器、低通滤波器、自适应陷波器等。由负载柔性引起的系统谐振，其频率和幅值常常并不固定，因而，很难使用固定的陷波器进行补偿。而低通滤波器虽然可以抑制一定频率之上的系统谐振，但往往限制了系统带宽并引入较大的相位滞后。文献[1,2]针对柔性负载引起的谐振抑制提出了一种自适应陷波滤波器，通过时时采集交流伺服电机中的转矩电流，在线计算谐振频率，并利用计算得到的谐振频率设计陷波滤波器，但系统动态响应相对于传统控制策略受到较大抑制。被动控制方法虽然在有些情况下可以抑制系统谐振，但需要消耗大量能量，并且控制方法会大大降低系统动态性能。主动控制方法主要采用状态反馈方法抑制系统谐振，主要包括基于状态反馈的极点配置控制策略、基于状态反馈的优化控制策略、基于状态反馈的鲁棒控制策略等。针对柔性负载特征引起的谐振，主动控制方法谋求从源头上对谐振进行抑制，而不是在谐振产生后再进行补偿。文献[3-5]分别对采用电机加速度反馈、负载加速度反馈、扭矩反馈控制策略对谐振抑制进行了研究，但主动控制方法往往需要增加额外的状态反馈信息(如负载加速度、柔性关节扭矩等)，增加了系统成本与复杂性。

在目前的研究中，则往往将神经网络、遗传算法等现代控制策略与状态反馈相结合抑制系统谐振。首先通过神经网络、遗传算法等对系统状态进行估计，然后将估计状态替代测量结果反馈至控制系统中。文献[6-12]分别利用模糊神经网络、基于混合灵敏度的状态估计策略以及基于滑模变结构的状态估计策略对系统状态进行估计，然后利用状态反馈策略抑制系统谐振。上述控制方法虽然在一些应用场合中可以取得良好的控制效果，但由于算法复杂、计算量大，在实际应用中尚不普遍。

实际高性能伺服系统中，控制策略仍以PI调节器为主，因而研究如何通过在PI调节器基础上引入适当的状态反馈从而最大程度地抑制负载柔性引起的谐振具有重要意义。目前针对柔性负载伺服驱动系统中的谐振抑制方法，虽然许多文献提出了一些针对特定系统的基于状态反馈的控制策略，但尚没有文献针对伺服系统中的机械谐振状态反馈策略进行统一的分析和研究。并且已有研究中柔性负载一般仅局限于双惯量系统这种最为简单的柔性负载系统，对于另一种常见的柔性连杆负载系统则很少涉及。文献[13-15]针对双惯量系统中状态反馈以及极点配置策略进行了研究，但是所提出的状态反馈策略仅适用于双惯量系统，无法应用于伺服电机驱动柔性连杆系统中。另外，文献在对伺服电机驱动柔性负载系统状态反馈策略进行分析时，往往仅通过仿真和实验进行说明，并没有从理论上对其参数确定方法进行分析，因而，分析结果在很多情况下并不能应用于实际系统中。

本文建立了对柔性关节和柔性连杆两种典型形式柔性负载进行描述的一致动力学模型，结合电机控制特性[16-18]，首先对采用PI调节器对系统进行控制时的系统特性进行了分析，然后将PI调节器应用于系统控制中，由于自由度有限，谐振抑制效果并不理想。因而，控制系统中需要引入状态反馈。针对谐振抑制的需要，通过增加一个额外的位置传感器对末段位置进行测量，然后将其反馈至控制系统中。针对负载位置反馈策略，分别分析了其应用范围、系统性能与参数关系、优势和劣势，并对其进行了极点配置。仿真和实验验证了本文所提出的基于负载位置状态反馈及其参数整定方法的有效性。

1 模型建立

1.1 柔性关节伺服驱动系统

在电气传动领域中，广泛应用的由一个柔性联轴器连接两个惯量的系统如图1所示。

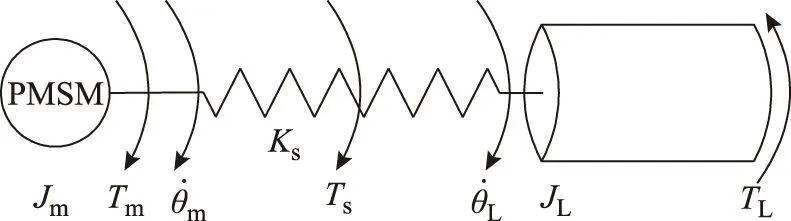
图1 典型双惯量系统模型Fig.1 Typical two mass system

图1中，Jm为电机转动惯量，Tm为电机输出转矩，θm为电机机械角度，ωm为电机机械角速度，JL为负载转动惯量，TL为负载转矩，θL为负载机械角度，ωL为负载机械角速度；Ks为柔性关节弹性系数；Ts为柔性关节扭矩。

对于双惯量系统，由于只有弹性联轴器一个弹性体，因而，其形变可以使用一阶振动模态进行描述。

定义

(1)

式中，Ia为系统总的转动惯量；Fa为谐振模态耦合系数；Ω为谐振频率。

整体系统的动能为

(2)

假设机械臂在水平面内运动，其势能由弹性变形产生。弹性势能为

(3)

将式(2)、式(3)代入拉格朗日方程(4)可以得到系统动力学方程(5)。

(4)

式中，qi(i=1,2)分别为电机机械角度θm和柔性连杆模态坐标η。

(5)

电机转速到电磁转矩、负载转速到电磁转矩的传递函数分别为

(6)

(7)

在上述系统模型中，可以通过参数Ω观察每一阶系统谐振频率，通过Fa观察每一阶模态频率的谐振程度。

1.2 柔性连杆伺服驱动系统

除1.1节中提到的柔性联轴器外，伺服系统中还广泛存在着另外一类柔性负载——柔性连杆，如工业机器人中的柔性机械臂等。柔性连杆伺服驱动系统如图2所示。图2中，u(x,t)为柔性连杆在x处的挠度，θm(t)为电机机械角度，Tm为电机输出转矩。

图2 柔性连杆伺服驱动系统Fig.2 System of flexible manipulator driven by servo motors

建模过程中，可将上述系统等效为中心刚体-悬臂梁系统。当中心刚体-悬臂梁系统做大范围运动时，柔性梁的横向弯曲振动比较明显，纵向振动相对可以忽略不计，因此，一般不考虑纵向变形的影响。在建模过程中，将其等效为欧拉-伯努利梁，即做如下假设：

1)只考虑横向振动，忽略轴向变形和剪切形变。

2)横向振动为小变形。

3)悬臂梁的长度远大于其截面尺寸。

在柔性连杆和电机轴上分别建立坐标系，一个动态坐标系O1X1Y1和一个静态坐标系OX0Y0。对于柔性连杆上任意一点，当柔性连杆发生弹性形变时，其在动态坐标系O1X1Y1中的位置u(x,t)，即为悬臂梁在x处的挠度。

根据振动理论，挠度可以表示为

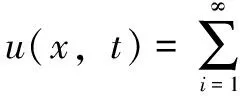
(8)

式中，φ(x)为模态函数；η为模态坐标。

同时，根据振动理论，欧拉-伯努利梁的横向振动方程可写为

(9)

式中，EI为柔性连杆的抗弯刚度；ρ为柔性连杆线密度；p(x,t)为作用在柔性连杆上的分布力。

悬臂梁的边界条件为

(10)

接下来，对振动模态φ(x)进行求解，不考虑外界作用力p(x,t)，将式(9)整理为

(11)

利用分离变量法进行求解，假设u(x,t)=φ(x)η(t)，将其代入式(9)可得

(12)

式(12)等号左边与x无关，等号右边与t无关，只可能等于常数，记作-ω2，得到

(13)

整理得到

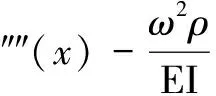
(14)

根据式(14)即可以确定悬臂梁弯曲振动的模态函数和频率,进而可以得到本征方程如式(15)所示。

φ(x)=eλx

(15)

λ4-β4=0

(16)

根据式(15)、式(16)即可以确定系统的各阶振动模态φi(x)。实际系统中，高阶模态不易被激发，因而通常对模态进行截断，取前N阶模态进行研究，即

(17)

柔性连杆在水平面内的运动可以看作是大范围刚体运动和小范围弹性变形运动的叠加，因此其上任意一点在OX0Y0坐标系的位置坐标(X,Y)可以表示为

(18)

柔性连杆的动能为

(19)

式中，ρ为柔性连杆线密度；A为柔性连杆横截面积。

假设柔性连杆在水平面内运动，其势能仅由弹性变形产生。弹性势能为

(20)

将式(19)、式(20)代入拉格朗日方程(21)，可以得到系统动力学方程(22)。

(21)

式中，qi(i=1,2,…,N+1)为伺服电机机械角度θm和柔性连杆第i阶模态坐标ηi(i=1,2,…,N+1)。

(22)

进一步的，假设柔性连杆转动惯量和模态频率分别为

(23)

(24)

各阶振动模态与电机轴转动之间的刚柔耦合系数为

Fa=[Fa1,Fa2,…,Fan]′

(25)

其中

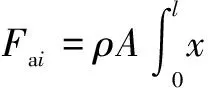
(26)

伺服电机驱动柔性连杆系统动力学方程为

(27)

式中，ξ为各阶振动模态阻尼系数矩阵。

柔性连杆末段位置为

(28)

如果仅考虑一阶模态，那么模态耦合系数向量Fa和谐振频率矩阵Ω将变为标量。可以得到简化后的柔性连杆驱动系统动力学方程为

(29)

柔性连杆末段位置为

θL(t)=θm(t)+Faη

(30)

该系统的传递函数为

(31)

从式(31)可以看出，在仅考虑一阶模态时，伺服驱动柔性连杆负载系统与上述柔性关节伺服驱动系统具有一致的结构，因而，可以利用动力学方程(27)统一描述伺服电机驱动柔性负载系统。

在式(27)所描述的动力学方程中，Ω表示系统振动频率，而Fa则可以表示每一阶振动频率的谐振程度，通过系统模型和参数可以很容易地观察系统谐振状况。另外，可以通过简单地增加Ω和Fa的阶次来描述含有更高阶振动频率的系统。

1.3 永磁同步电机数学模型

永磁同步电机由于具有结构简单、损耗小、效率高、可靠性高等优点，广泛应用于高性能交流伺服系统中。在功率不变原则下，永磁同步电机在dq坐标系下的数学模型为

(32)

电磁转矩表达式为

Tm=pn[ψriq+(Ld-Lq)idiq]

(33)式中，ud、uq分别为定子侧的d、q轴电压；id、iq分别为定子侧的d、q轴电流；Rs为定子侧电枢电阻；ωm为转子机械角速度；Ld、Lq分别为定子侧的d、q轴电感；ψr为转子永磁体在定子绕组中产生的磁链，即转子永磁磁链；pn为转子极对数；Tm为电机输出电磁转矩。

这里以隐极式永磁同步电机为例，因而永磁同步电机数学模型和转矩方程简化为

(34)

Tm=pnψriq

(35)

1.4 永磁同步电机驱动柔性负载数学模型

在永磁同步电机驱动柔性负载系统中，永磁同步电机输出电磁转矩作为柔性负载的驱动转矩驱动柔性负载，柔性负载的位置角度反过来影响永磁同步电机转矩环。因而，按照上述思路，将1.3节中永磁同步电机与1.2节中柔性负载的数学模型结合，可得到永磁同步电机驱动柔性负载的动力学方程。

但在永磁同步电机驱动系统中，由于柔性负载的谐振频率与电流环带宽差别较大，因而，柔性对于永磁同步电机电流环的影响较小。可以认为在速度外环进行调节时，电流内环已经调节完成。

因而，可以得到简化后永磁同步电机驱动柔性负载的动力学方程为

(36)

2 PI控制策略

不考虑电流内环的影响，采用PI调节器时，速度外环如图3所示。

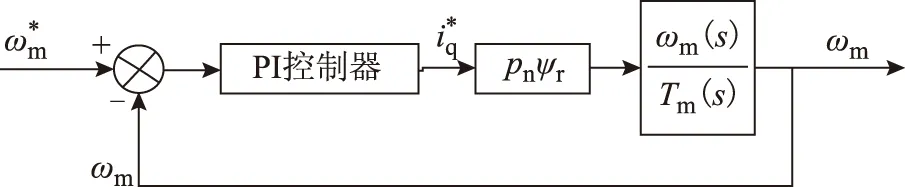
图3 传统PI控制策略控制框图Fig.3 Application of PI controller to the system of flexible manipulator driven by servo motors

如果不考虑阻尼系数的影响，上述系统传递函数与典型双惯量系统传递函数类似。本文借鉴文献[4]提出的双惯量系统极点配置方法对极点进行配置。不考虑阻尼影响采用PI调节器时系统闭环传递函数为

(37)

式中，kP、kI分别为PI调节器参数。

分母多项式可以整理为

式中，ω1、ω2为极点的自然频率；ξ1、ξ2为极点的阻尼系数。

由

整理得到

(38)

此时控制系统闭环零点为

(39)

式(38)、式(39)建立了两对极点、零点与系统PI参数之间的关系。由于存在两对极点，而只有kP、kI两个可调参数，因而需要选定两个限制条件才能确定零极点的位置，所以谐振抑制效果并不理想。为了更好地抑制谐振，需要引入额外的状态反馈信息。

3 负载位置反馈策略

(40)

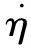
θL(t)=θm(t)+Faη

因而可以通过测量柔性关节系统负载位置或柔性连杆系统末段位置获得柔性模态幅值η，进一步通过微分获得其导数信息。

这里通过引入末段位置反馈抑制系统谐振，并对其应用范围、系统性能与参数关系、优势和劣势进行分析，然后通过极点配置确定控制器参数。

结合图3，此时系统控制框图如图4所示。

图4 负载位置反馈控制策略控制框图Fig.4 Control blocks of PI controller with load position feedback

结合式(36)，系统方程为

(41)

不考虑阻尼影响，系统闭环传递函数为

(42)

式中，kP、kI分别为PI调节器参数；k1为柔性模态幅值η反馈系数。

分母多项式可以整理为

式中，ω1、ω2为极点的自然频率；ξ1、ξ2为极点的阻尼系数。

由

pnψrkPΩ2s+pnψrkIΩ2

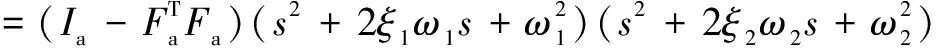
(43)

此时控制系统闭环零点为

z2=jΩ,z3=-jΩ

(44)

这里，有kP、kI、k1三个参数可调，因而，零极点不能任意配置。根据式(43)，需要满足的限制条件为

(45)

根据文献[4]中的极点配置方法，分别选择：

1)相同极点阻尼系数极点配置策略。

考虑ξ1=ξ2=ξ，那么根据式(43)整理得到

Ω2=ω1ω2

假设

ω1<Ω,ω2>Ω

此时相同极点阻尼系数极点配置零极点分布如图5 所示。

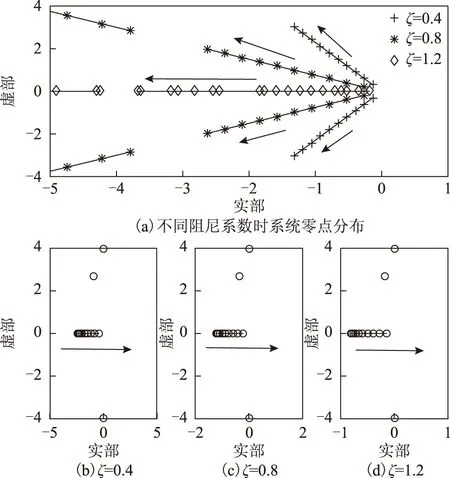
图5 相同极点阻尼系数极点配置零极点分布Fig.5 Poles and zeros of the pole placement strategy with same friction

根据图5可以看出，在相同极点阻尼系数极点配置策略下，随着阻尼系数增大，零点靠近虚轴，主导极点远离虚轴，动态响应变快，谐振减弱；随着ω1的增大，ω2的减小，零点靠近虚轴，极点远离虚轴，动态响应变快，谐振减弱。

2)相同极点实部极点配置策略。

考虑ξ1ω1=ξ2ω2=aΩ，根据式(43)整理得到

假设

此时相同极点实部极点配置零极点分布如图6所示。

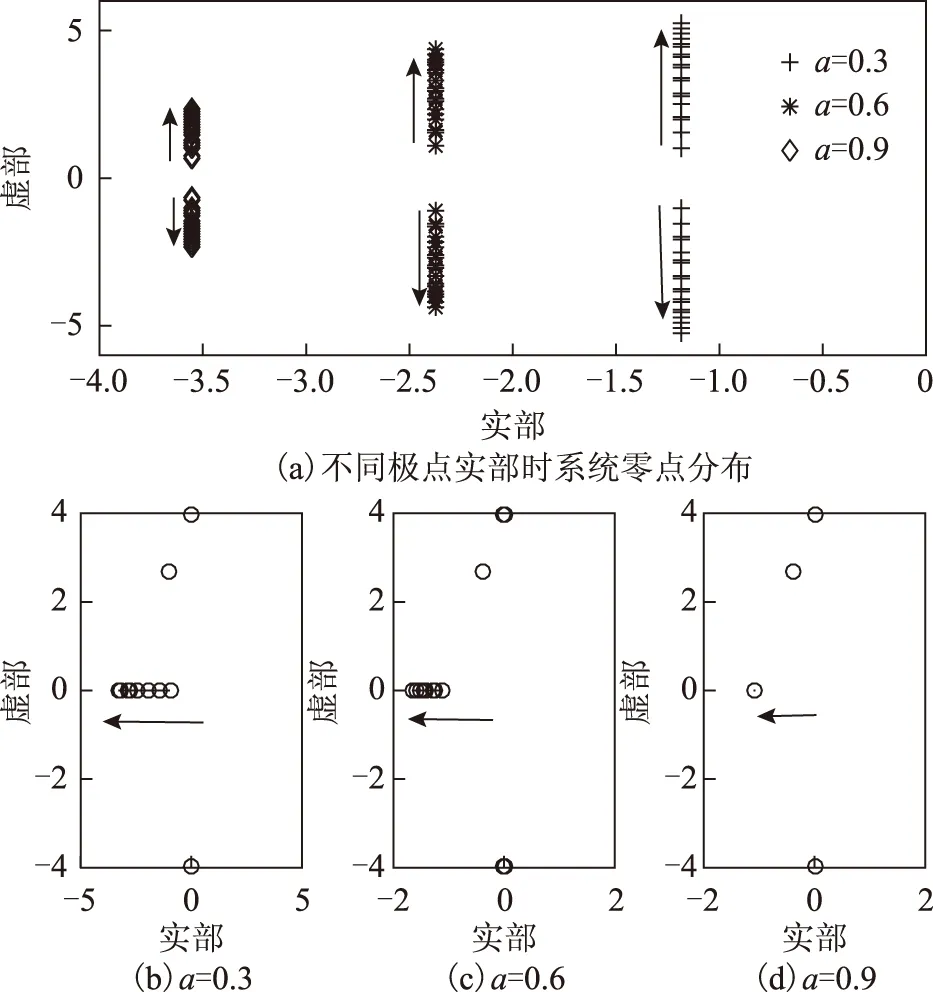
图6 相同极点实部极点配置零极点分布Fig.6 Poles and zeros of the pole placement strategy with real part

根据图6可以看出，在相同实部极点配置策略下，随着极点实部的增大，参数选取范围变小，极点远离虚轴，零点接近虚轴，动态响应加快，谐振减弱；在极点实部确定的情况下，随着ω1的增大，ω2的减小，零点远离虚轴，谐振增强。

3)相同极点幅值极点配置策略。

考虑ω1=ω2，根据式(43)整理得到

ω1=ω2=Ω

此时相同极点幅值极点配置零极点分布如图7所示。

图7 相同极点幅值极点配置零极点分布Fig. 7 Poles and zeros of the pole placement strategy with same amplitude

进一步的，若其中一对极点阻尼系数为0，则

ξ1=0,ω1=ω2=Ω

此时闭环极点为

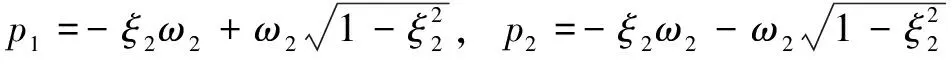
p3=jΩ,p4=-jΩ

零点为

可以看出，其中一对零极点相互抵消，柔性负载系统等效为刚性系统。

根据图7可以看出，在相同极点幅值极点配置策略下，两对极点相互独立，随着两对极点阻尼系数的减小，零点接近虚轴，同时零极点距离缩短，此时谐振减弱；若其中一对极点阻尼系数为0，柔性负载系统等效为刚性系统，此时，可以按照刚性系统极点配置方法确定控制系统参数。

4 仿真结果

仿真通过Simulink进行，仿真所使用的模型为式(34) 永磁同步电机驱动柔性负载模型。系统参数见表1。

表1 柔性负载模型参数

对电机进行转速控制，引入负载位置反馈，分别采用相同阻尼系数、相同实部、相同极点幅值三种极点配置策略确定PI参数，进行仿真。然后与无负载位置反馈时PI调节器控制效果进行对比。

4.1 相同阻尼系数极点配置

分别选定阻尼系数，计算得到的PI参数和零极点分布见表2。仿真结果如图8所示。其中图8a、图8b分别为采用表2中第1、2组控制系统参数的仿真结果；图8c、图8d分别为采用表2中第1、2组的控制系统参数但未引入负载位置反馈的仿真结果。

对图8中系统的动态性能指标进行总结可以得到表3，其中tr为上升时间，σ%为超调量，ts(5%)为稳定时间。

根据仿真结果可以看出，在相同阻尼系数极点配置策略下，观察表3可以看出，随着阻尼系数增大，动态响应变慢，谐振减弱；随着ω1的增大，ω2的减小，动态响应变快，谐振程度增强；相对于未引入负载位置反馈PI调节器，引入负载位置反馈能够更好地抑制系统谐振。

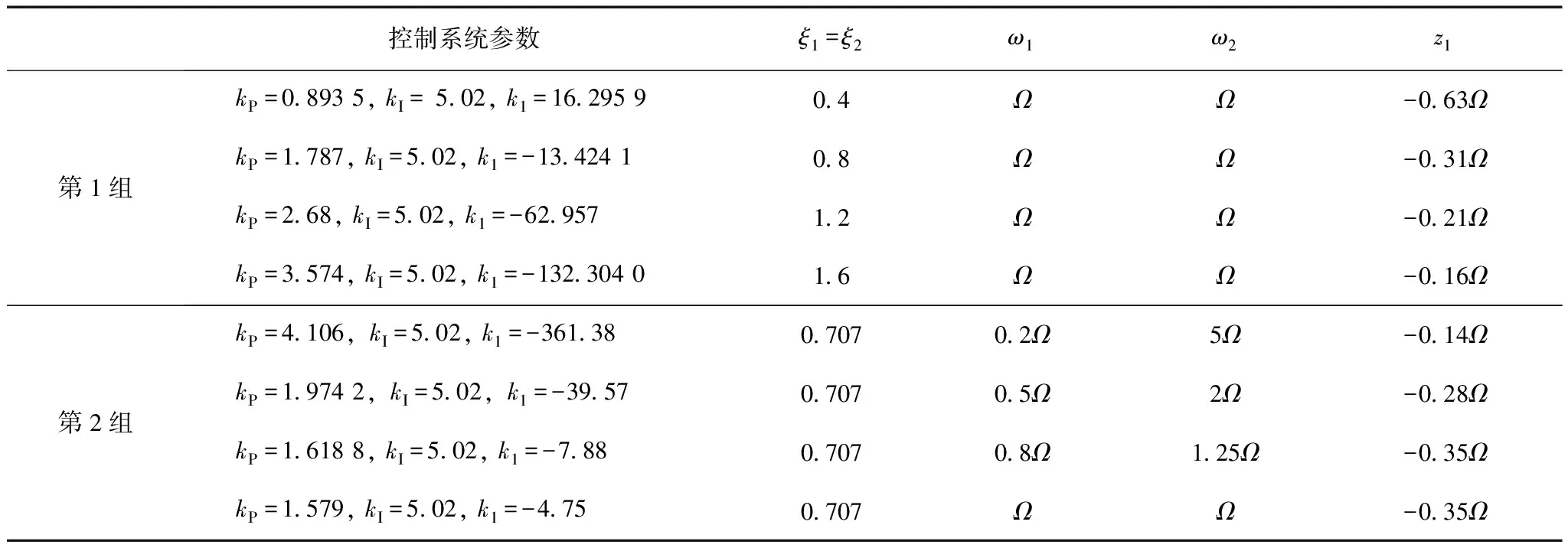
表2 极点阻尼系数相等配置策略零极点位置以及控制系统参数

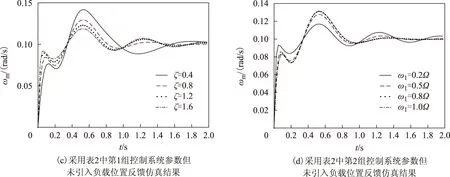
图8 相同极点阻尼系数极点配置策略仿真结果Fig.8 Simulation results with the pole placement strategy of same friction

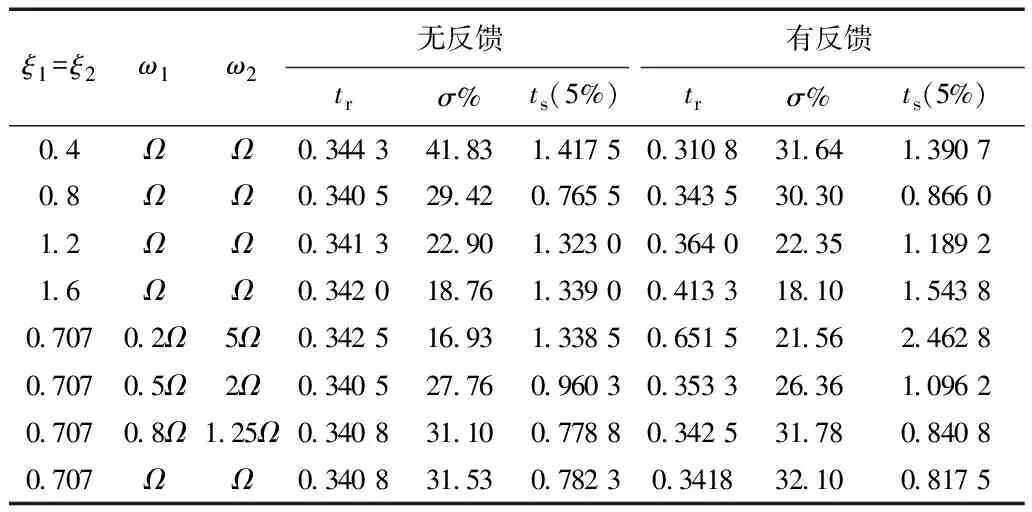
表3 极点阻尼系数相等配置策略仿真结果

4.2 相同极点实部极点配置策略

分别选定极点实部，计算得到的PI参数和零极点分布见表4。仿真结果如图9所示，其中图9a、图9b分别为采用表4中第1、2组控制系统参数的仿真结果；图9c、图9d分别为采用表4中第1、2组控制系统参数但未引入负载位置反馈的仿真结果。

对图9中系统的动态性能指标进行总结可得到表5。根据仿真结果可以看出，在相同实部极点配置策略下，由表5可以看出，随着极点实部的增大，动态响应变慢，谐振减弱；在极点配置过程中，参数选择范围较小，因而，谐振抑制效果与PI调节器相差不大。

表4 极点阻尼实部相等配置策略零极点位置以及控制系统参数

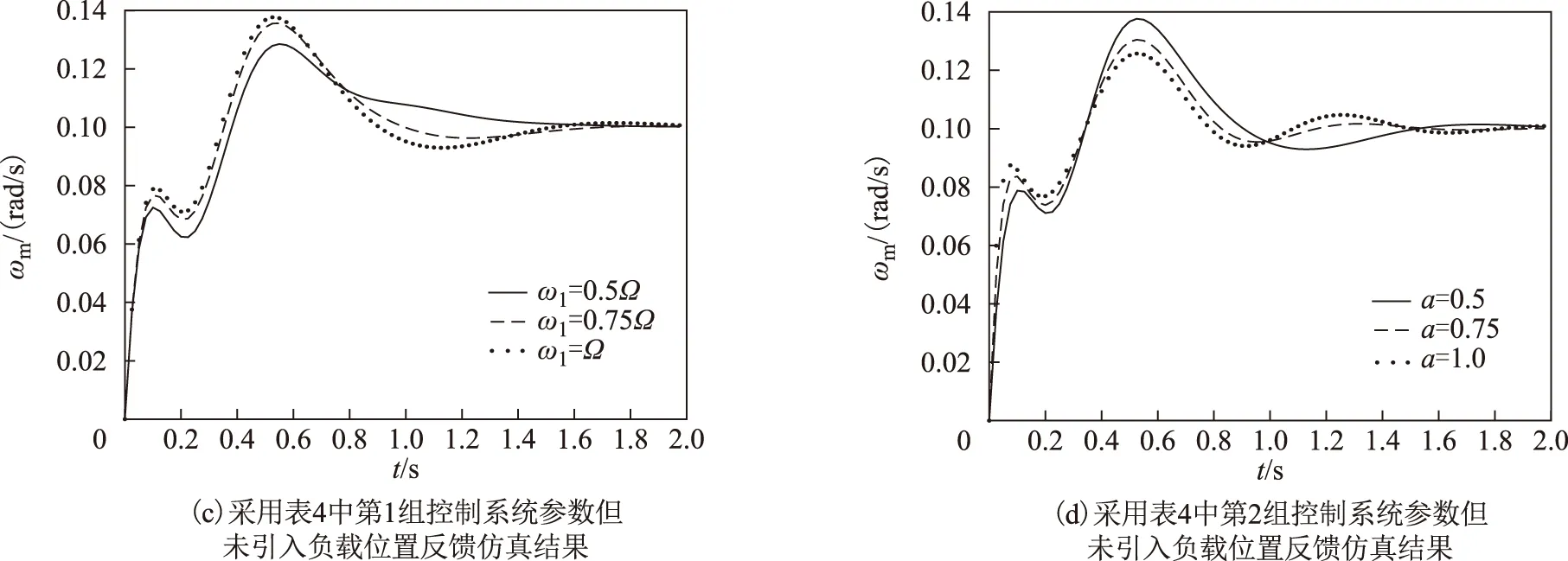
图9 相同极点实部极点配置策略仿真结果Fig.9 Simulation results with the pole placement strategy of same real part

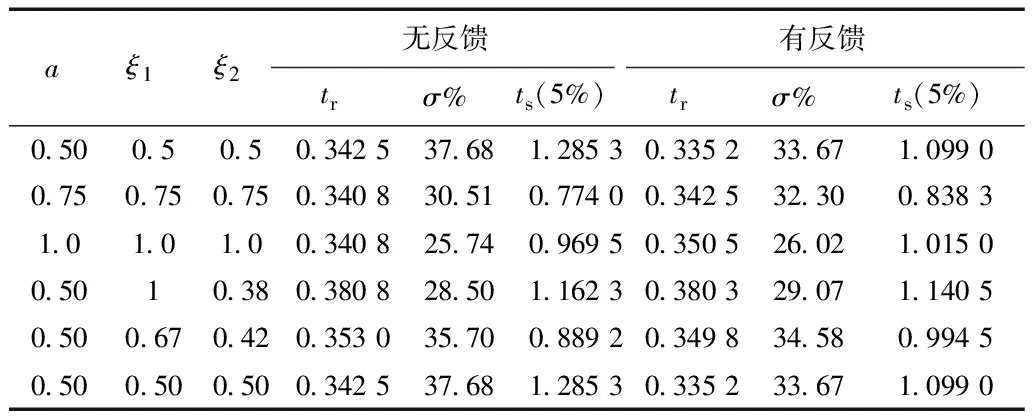
表5 极点阻尼系数相等配置策略仿真结果

4.3 极点幅值相等极点配置策略

分别选定阻尼系数，计算得到的PI参数和零极点分布见表6。仿真结果如图10所示，其中图10a、图10b分别为采用表6中第1、2组控制系统参数的仿真结果；图10c、图10d分别为采用表6中第1、2组控制系统参数但未引入负载位置反馈的仿真结果。

对图10中系统的动态性能指标进行总结可得到表7。

根据仿真结果可以看出，在相同幅值配置策略下，由表7可以发现，两对极点相互独立，随着极点阻尼系数的增大，谐振减弱；相对于未引入负载位置反馈PI调节器，引入负载位置反馈能更好地抑制系统谐振。

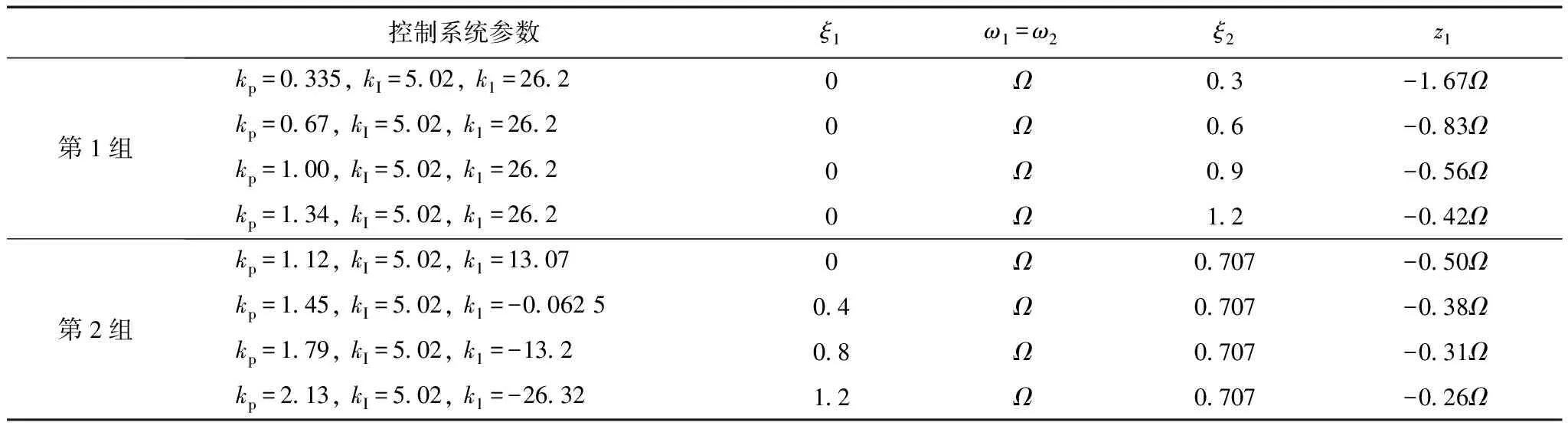
表6 极点幅值相等配置策略零极点位置以及控制系统参数

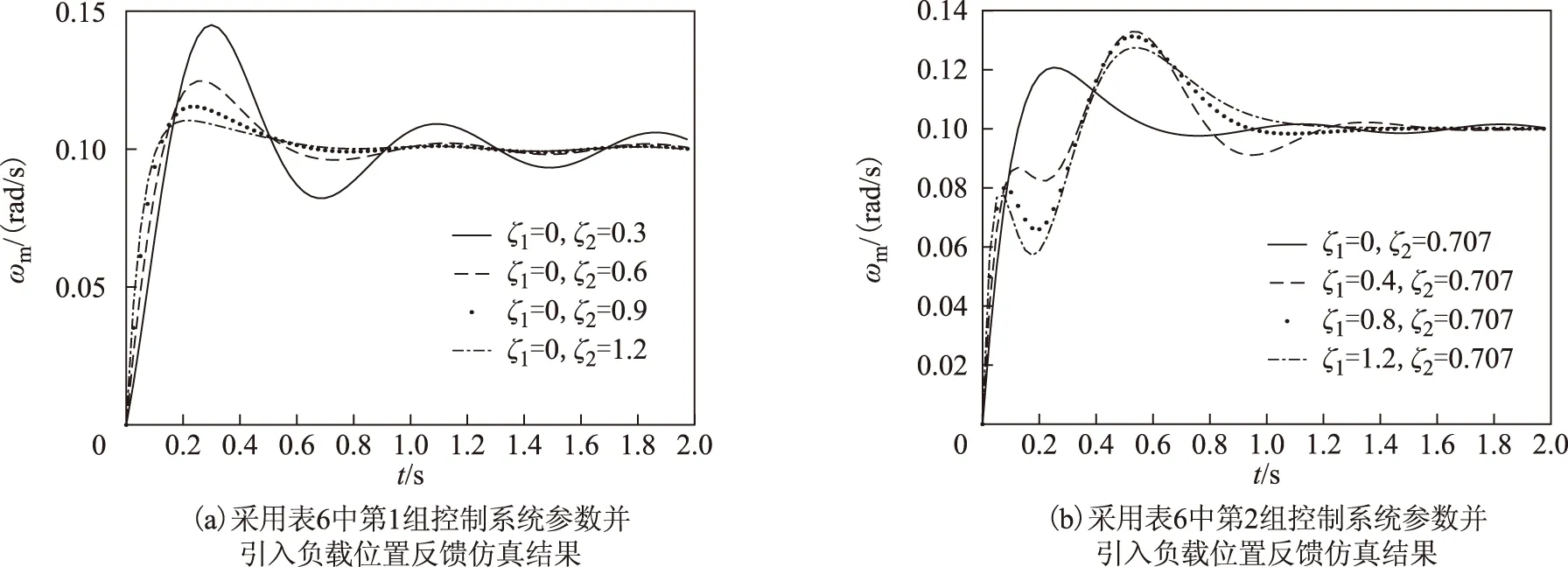
图10 相同极点幅值极点配置策略仿真结果Fig.10 Simulation results with the pole placement strategy of same amplitude

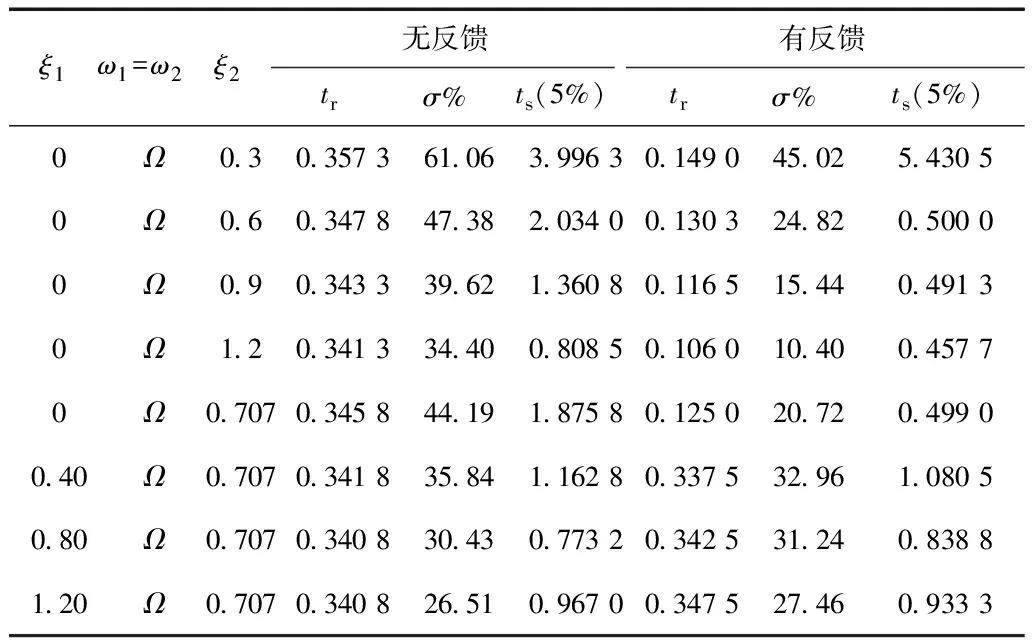
表7 极点阻尼系数相等配置策略仿真结果

5 实验结果

实验在卡内基梅隆大学蛇形机器人两个模块上进行，两个模块之间由一弹性元件相连。系统参数见表8。

对系统进行速度控制，引入负载位置反馈，分别采用提出的3种极点配置策略。根据式(1)中的定义可以发现，系统参数与表1中仿真所使用柔性负载模型参数一致，因而这里3种极点配置策略实验参数分别与表2、表4、表6相同，实验结果分别如图11～图13 所示。图11为采用相同极点阻尼系数极点配置策略实验结果，其中图11a、图11b分别为采用表2中第1、2组的控制系统参数的实验结果；图11c、图11d 分别为采用表2中第1、2组的控制系统参数但未引入负载位置反馈的实验结果。图12为采用相同极点阻尼系数极点配置策略实验结果，其中，图12a、图12b分别为采用表4中第1、2组的控制系统参数的实验结果；图12c、图12d分别为采用表4中第1、2组的控制系统参数但未引入负载位置反馈的实验结果。图13为采用相同极点阻尼系数极点配置策略实验结果，其中，图13a、图13b分别为采用表6中第1、2组的控制系统参数的实验结果；图12c、图12d分别为采用表6中第1、2组的控制系统参数但未引入负载位置反馈的实验结果。

对图11中系统的动态性能指标进行总结可得到表9。

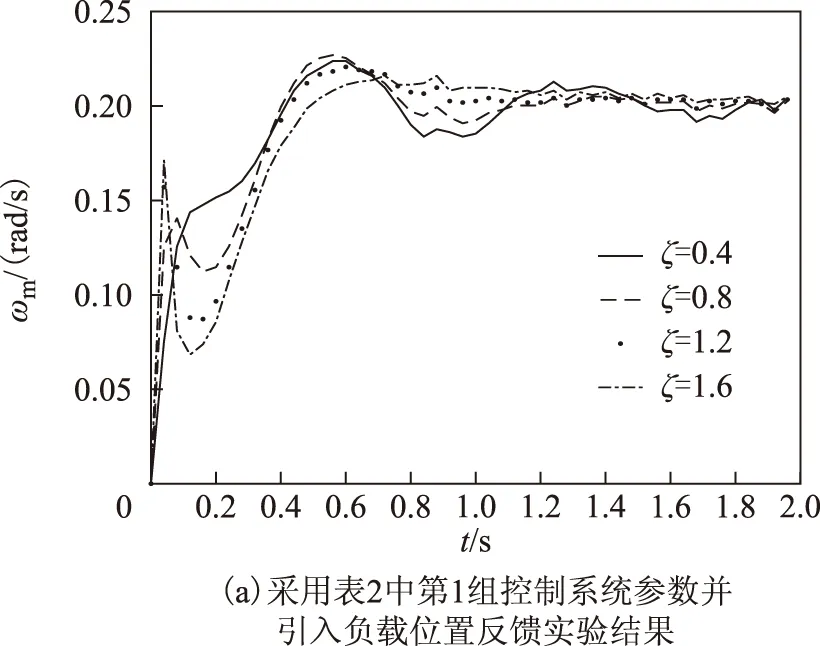
图11 相同极点阻尼系数极点配置策略实验结果Fig.11 Experimental results with the pole placement strategy of same friction

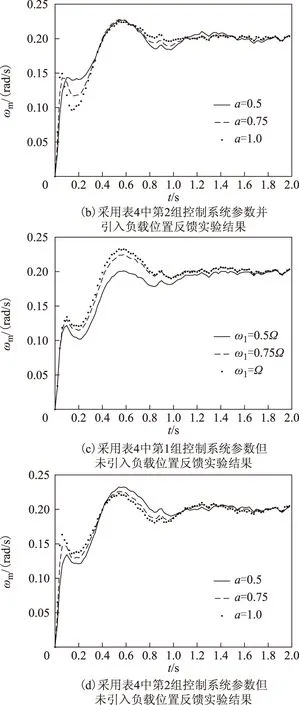
图12 相同极点实部极点配置策略实验结果Fig.12 Experimental results with the pole placement strategy of same real part

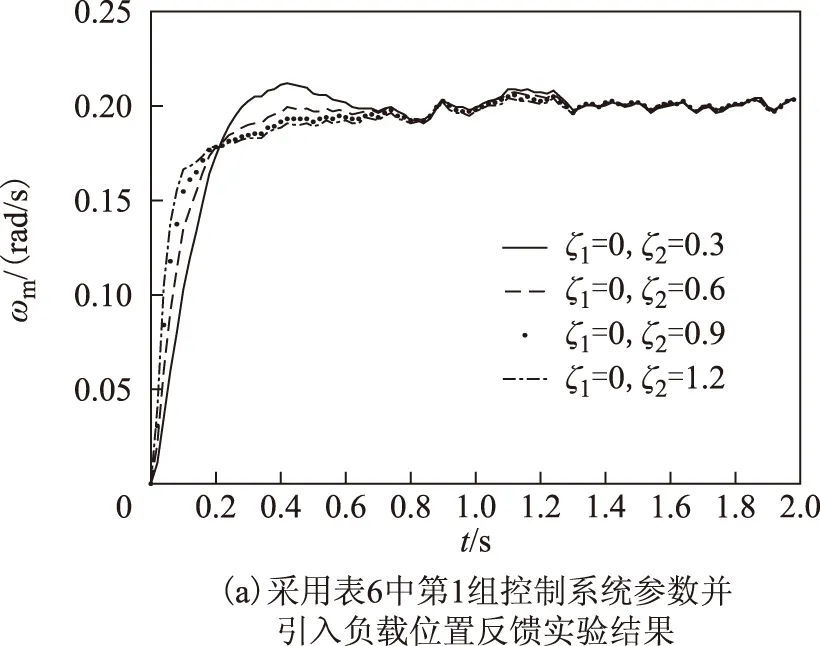
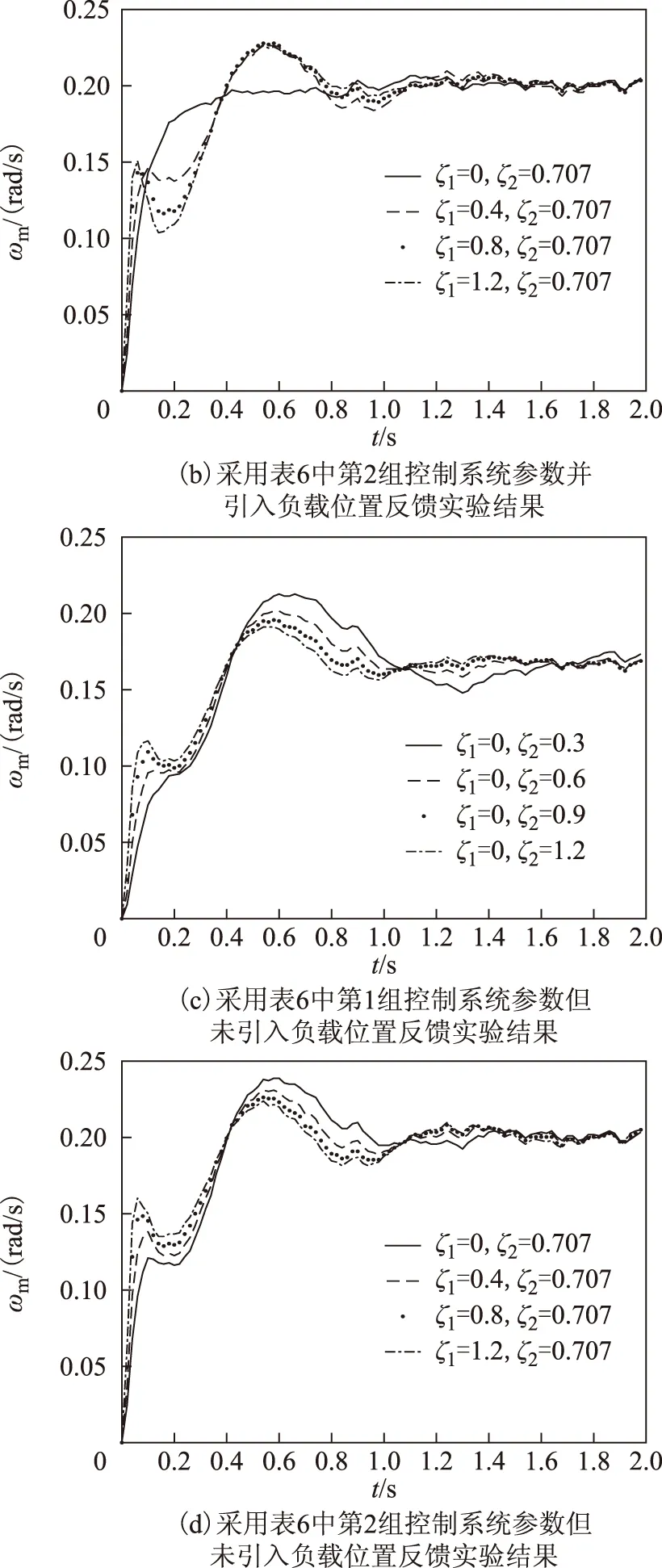
图13 相同极点幅值极点配置策略实验结果Fig.13 Experimental results with the pole placement strategy of same amplitude

表9 极点阻尼系数相等配置策略仿真结果

对图12中系统的动态性能指标进行总结可得到表10。

表10 极点实部相等配置策略仿真结果

对图13中系统的动态性能指标进行总结可得到表11。

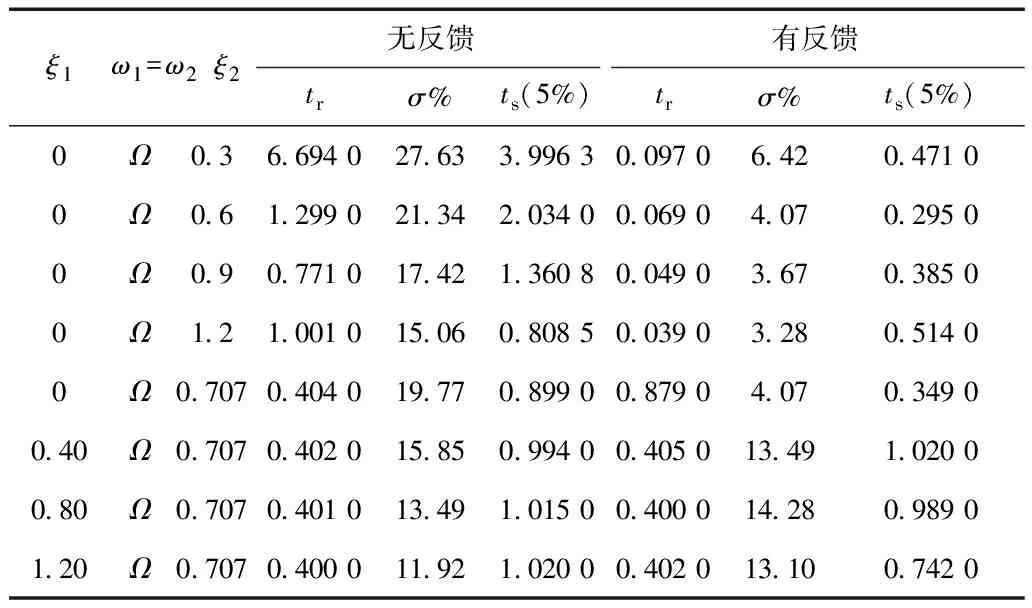
表11 极点幅值相等配置策略仿真结果

由表9～表11可以发现，实验中，由于摩擦和阻尼的影响，相对于仿真结果略有不同，但基本响应与仿真结果一致，因而通过实验可得到与仿真中一致的结论。

综上所述，通过引入负载位置反馈，可以在传统PI调节器的基础上进一步抑制系统谐振；在对基于负载位置反馈的永磁同步电机驱动柔性负载进行极点配置时，优先考虑阻尼系数相等和极点幅值相等极点配置策略；在相同阻尼系数极点配置策略中，为了抑制系统谐振，可以考虑尽可能增大阻尼系数并且使得两对极点幅值相等；在相同极点幅值极点配置策略下，可以通过选择参数使得一对极点与一对零点相互抵消，使系统等效为刚性系统，然后通过选择另外一对极点阻尼系数进行极点配置。

6 结论

针对永磁同步电机驱动柔性负载中的机械谐振，本文利用拉格朗日原理对伺服系统中的柔性关节和柔性连杆负载建立了一致的数学模型。在此基础上，与永磁同步电机数学模型结合，得到了永磁同步电机驱动柔性负载数学模型。采用PI调节器对系统进行控制，并对PI调节器参数与系统极点关系进行了分析。分别引入3种不同类型的针对PI调节器的极点配置策略，通过仿真和实验对PI调节器和3种状态反馈策略进行了评估。得到如下结论：

1)本文所提出的永磁同步电机驱动柔性负载建模方法，综合考虑了永磁同步电机数学模型和柔性负载数学模型，同时柔性负载模型既可以表示柔性关节系统也可以表示柔性连杆系统，更具有一般性和代表性。

2)本文所提出的采用PI调节器对永磁同步电机驱动柔性负载系统进行极点配置的方法，能够使得PI调节器参数与系统极点关系一目了然，对PI调节器参数整定具有重要意义。

3)通过引入负载位置反馈，可以在传统PI调节器的基础上进一步抑制系统谐振。

4)在对基于负载位置反馈的永磁同步电机驱动柔性负载系统进行参数整定时，优先考虑阻尼系数相等和极点幅值相等极点配置策略；在相同阻尼系数极点配置策略中，为了抑制系统谐振，可以考虑尽可能增大阻尼系数并且使得两对极点幅值相等；在相同极点幅值极点配置策略下，可以通过选择参数使得一对极点与一对零点相互抵消，然后通过选择另外一对极点阻尼系数进行极点配置。

[1] Ghorbel F，Hung J Y，Spong M W.Adaptive control of flexible-joint manipulators[J].IEEE Control Systems Magazine，1989，9(7)：9-13.

[2] O′Sullivan T M，Bingham C M，Schofield N.High-performance control of dual-inertia servo-drive systems using low-cost integrated SAW torque transducers[J]. IEEE Transactions on Industrial Electronics，2006，53(4)：1226-1237.

[3] Li Wen，Hori Y.Vibration suppression using single neuron-based PI fuzzy controller and fractional-order disturbance observer[J].IEEE Transactions on Industrial Electronics，2007，54(1)：117-126.

[4] Szabat K，Orlowska-Kowalska T，Dybkowski M.Indirect adaptive control of induction motor drive system with an elastic coupling[J].IEEE Transactions on Industrial Electronics，2009，56(10)：4038-4042.

[5] Bang J S，Shim H，Park S K，et al.Robust tracking and vibration suppression for a two-inertia system by combining backstepping approach with disturbance observer[J]. IEEE Transactions on Industrial Electronics，2010，57(9)：3197-3206.

[6] Yun J N，Su Jianbo，Kim Y I，et al.Robust disturbance observer for two-inertia system[J].IEEE Transactions on Industrial Electronics，2013，60(7)：2700-2710.

[7] 杨明，郝亮，徐殿国.基于自适应陷波滤波器的在线机械谐振抑制[J].哈尔滨工业大学学报，2014，46(4)：63-69. Yang Ming，Hao Liang，Xu Dianguo.Online suppression of mechanical resonance based on adapting notch filter[J].Journal of Harbin Institute of Technology，2014，46(4)：63-69.

[8] Wang Zidong，Zeng Hanqing，Ho D W C，et al.Multiobjective control of a four-link flexible manipulator：a robust H∞ approach[J].IEEE Transactions on Control Systems Technology，2002，10(6)：866-875.

[9] Rokui M R，Khorasani K.Experimental results on discrete-time nonlinear adaptive tracking control of a flexible-link manipulator[J]. IEEE Transactions on Systems，Man，and Cybernetics，Part B：Cybernetics，2000，30(1)：151-164.

[10]Su Zhihong，Khorasani K.A neural-network-based controller for a single-link flexible manipulator using the inverse dynamics approach[J].IEEE Transactions on Industrial Electronics，2001，48(6)：1074-1086.

[11]Benosman M，Le Vey G.Stable inversion of SISO nonminimum phase linear systems through output planning：an experimental application to the one-link flexible manipulator[J].IEEE Transactions on Control Systems Technology，2003，11(4)：588-597.

[12]Martins J M，Mohamed Z，Tokhi M O，et al.Approaches for dynamic modelling of flexible manipulator systems[J]. IEE Proceedings-Control Theory and Applications，2003，150(4)：401-411.

[13]Diaz I M，Pereira E，Feliu V，et al.Concurrent design of multimode input shapers and link dynamics for flexible manipulators[J].IEEE/ASME Transactions on Mechatronics，2010，15(4)：646-651.

[14]Pereira E，Aphale S S，Feliu V，et al.Integral resonant control for vibration damping and precise tip-positioning of a single-link flexible manipulator[J].IEEE/ASME Transactions on Mechatronics，2011，16(2)：232-240.

[15]刘才山，王建明，阎绍泽，等.柔性机械臂非线性动力学模型及控制的研究[J].振动工程学报，1998，11(2)：152-157. Liu Caishan，Wang Jianming，Yan Shaoze，et al.Study of dy namic model and co nt rol of a flexible beam[J].Journal of Vibration Engineering，1998，11(2)：152-157.

[16]夏长亮, 阎彦. 矩阵变换器-永磁同步电机系统[J]. 电工技术学报, 2015, 30(23): 1-9. Xia Changliang, Yan Yan. Matrix converter permanent magnet synchronous motor drives[J]. Transactions of China Electrotechnical Society, 2015, 30(23): 1-9.

[17]符慧, 左月飞, 刘闯, 等. 永磁同步电机转速环的一种变结构 PI 控制器[J]. 电工技术学报, 2015, 30(12): 237-242. Fu Hui, Zuo Yuefei, Liu Chuang, et al. A variable structure PI controller for permanent magnetic synchronous motor speed-regulation system[J]. Transactions of China Electrotechnical Society, 2015, 30(12): 237-242.

[18]谷鑫, 胡升, 史婷娜, 等. 基于神经网络的永磁同步电机多参数解耦在线辨识[J]. 电工技术学报, 2015, 30(6): 114-121. Gu Xin, Hu Sheng, Shi Tingna, et al. Muti-parameter decoupling online identification of permanent magnet synchronous motor based on neural network[J]. Transactions of China Electrotechnical Society, 2015, 30(6): 114-121.

(编辑 于玲玲)

Resonance Suppression Method Based on Load Position Feedback for Flexible Load Driven by PMSM

DingYoushuangXiaoXi

(State Key Laboratory of Security Control and Simulation of Power Systems and Large Scale Generation Equipment Department of Electrical Engineering Tsinghua University Beijing 100084 China)

The flexible load is widely presents in the electrical drive system. According to the origin, the flexible load can be classified as the system of rigid load driven by a servo motor via a flexible coupling and flexible load driven directly by a servo motor. As for the typical system above, firstly they are modeled according to Lagrange Principle and an equivalent model is acquired. Then PI controller is used for the system control. Since there are only two degrees for PI controller, the performance is unsatisfactory. As a result, the state feedback has to be introduced. On this occasion, the load position is measured and feedback to the control system. Then the strategy is analyzed and the parameters are tuned with pole placement method. The simulation and experimental results verified the effectiveness of the load position feedback strategy and its′ parameter tuning method for the system of flexible load driven by PMSM.

Permanent magnet synchronous motor(PMSM), flexible load, load position feedback, pole placement

国家自然科学基金项目资助(51577095)。

2016-02-18 改稿日期2016-06-07

TM315

丁有爽 男，1991年生，博士研究生，研究方向为交流电机、工业机器人驱动控制。

E-mail: dingyoushuang@126.com(通信作者)

肖 曦 男，1973年生，博士，教授，博士生导师，研究方向为交流电机控制、电力储能、海浪发电等。

E-mail: xiao_xi@mail.tsinghua.edu.cn