基于鲁棒优化的网架重构机组恢复顺序优化

焦 洁 刘 艳

(华北电力大学电气与电子工程学院 保定 071003)



基于鲁棒优化的网架重构机组恢复顺序优化

焦 洁 刘 艳

(华北电力大学电气与电子工程学院 保定 071003)

在当前以火电为主的系统中，大停电后机组恢复时间的长短对重构效果影响显著。针对机组启动准备时段和启动时段可能出现的时间延迟，以最小化重构期间的电量不足为优化目标，构建了计及火电机组启动时间不确定性的机组恢复顺序鲁棒优化模型。通过交叉粒子群算法与CPLEX优化求解相结合，可获得量化表征恢复效果和运行可靠性的机组恢复顺序，为调度人员应对可能出现的最严重机组恢复迟滞场景提供了更加全面的决策参考。对于调度人员自行拟定的机组恢复顺序，还可根据运行经验预估其成功实施的概率，通过CPLEX求解并筛选关键时步，为调度人员有的放矢地保证恢复效果提供量化指导。针对新英格兰10机39节点系统和某区域电网的仿真结果验证了该方法的有效性。

网架重构 机组恢复 机组启动时间不确定性 鲁棒优化

0 引言

在电力系统结构日趋完善、监视控制水平逐渐提高的大背景下，由于某些偶然和必然因素的存在，大停电事故依然是现在电力系统必须面对的严重威胁[1,2]。因此，符合实际、切实可行的黑启动恢复方案的制定是保证系统能够安全、快速恢复的重要措施[3,4]。极端情况下的黑启动恢复涉及系统控制运行的诸多方面，需要经历黑启动、网架重构和负荷恢复3个阶段[5,6]。从整体看，机组恢复是整个恢复控制的基础，而在以火电机组为主的实际系统中机组恢复会受到源于机组自身或外部系统的诸多不确定因素的影响，恢复控制的难度将进一步增大。因此，能够综合考虑恢复过程中可能的不确定因素对机组序列安全高效启动和对网架重构过程中系统发电能力的快速恢复至关重要。

针对网架重构过程机组恢复顺序问题，国内外学者的研究已有很多。文献[7]将时间和发电量作为影响机组恢复的主要因素，建立了电力系统事故后机组恢复次序的层次结构模型。文献[8]以最大化恢复过程中机组发电量为目标，将机组恢复顺序等效为多约束条件下的背包问题，利用回溯算法定量求解机组恢复顺序的最优解。文献[9]将机组启动顺序的确定简化为一个混合整数线性优化问题。相对于启发性方法，该方法以线性规划的方式得到所有机组初始启动顺序的最优解。为了进一步计及可能影响恢复速度的不确定因素，文献[10]以最大化网架重构过程的净收益为目标，计及了恢复操作时间的不确定性，建立了网架重构方案优化的机会约束规划模型。文献[11,12] 基于风险理论计及恢复过程中线路投运的不确定性。文献[13]考虑线路投运过程中操作时间的不确定性，建立基于模糊机会约束的网架重构优化模型保证重构过程的顺利进行。然而，影响网架重构过程的不确定因素除上述研究中重点考虑的线路投运过程以外，还有机组自身启动过程的不确定性。机组恢复是系统发电能力恢复的基础，其不确定性对网架重构的效率有较大影响。文献[14]用已投运机组的停运概率表征机组投运过程的不确定性。文献[15]在计及投运机组停运可能性的基础上，以系统恢复过程中机组投运风险最小为目标优化机组恢复顺序。事实上，机组启动过程的不确定不仅体现为机组投运失败的可能性，更为常见的是机组启动过程的延时。针对以火电机组为主要电源组成的系统而言，这一点将会极大地影响重构效果。

在上述背景下，本文首先从单台火电机组的启动过程入手，分析可能导致恢复延时的原因，进而讨论了大停电后多台火电机组相继恢复时所出现的时间迟滞场景。在此基础上，通过引入不确定时步长度对可能延时恢复场景下系统重构过程的电量不足进行量化表示，建立了最小化该电量不足的机组恢复顺序鲁棒优化模型，所获得的机组恢复方案将为调度人员应对可能出现的最严重的机组恢复迟滞场景提供决策参考。对于既定的恢复方案，根据模型中鲁棒控制参数的选取，从恢复效果和运行可靠性方面对相应的恢复预案进行定量评估。寻找恢复过程的关键时步，保证恢复时间在一定的限值内，从而可保证恢复效果。

1 火电机组启动过程不确定因素对重构效果的影响分析

网架重构阶段的主要任务是通过优化机组的投运和充电关键线路，以尽可能短的时间最大限度地恢复系统的发电能力。在整个重构过程中，机组和线路的恢复相互交织彼此影响。但是，在当前火电机组为主要电源的系统中，如果大停电造成机组停机，由于火电机组恢复耗时较长，期间还要受到诸多不确定因素的影响，因此，机组恢复对重构效果的影响较为显著。

首先，对一台火电机组的启动投运过程进行简要分析。

图1所示为火电机组的投运出力曲线。图中tip、tie和tic分别为机组i的预备启动时刻、辅机带电时刻和并网带负荷时刻。tip是指调度下令准备启动机组i的时刻。接到指令后，从送电端到受电端的相关厂站开始进行增出力准备、倒闸操作、充电线路和必要的厂用辅机投运准备。如果假设0时刻开始进入停电后的网架重构阶段，tip主要由调度预先确定的机组恢复顺序决定。辅机带电时刻tie是指完成所有送电和受电准备后，机组i厂用辅机带电，其后机组才真正进入启动程序。在这期间，机组i尚未恢复发电能力，需由黑启动机组或初期已恢复的小系统为其供电。从tic开始，机组i并网，并根据调度要求接带负荷。可以看出，从机组预备启动至并网的时间越长，系统发电能力的恢复速度越慢，重构效率越低。就可能影响该时间的主要因素来看，启动准备时段长度(tip～tie)取决于黑启动电源或初期带电系统的升负荷速度以及与恢复机组i相关的送电路径组建速度；启动时段长度(tie～tic)受机组热力系统特性影响，与机组的停机时间(0～tie时段长度)密切相关。显然，后续机组要受到之前多台机组恢复累计时间tip的较大影响。

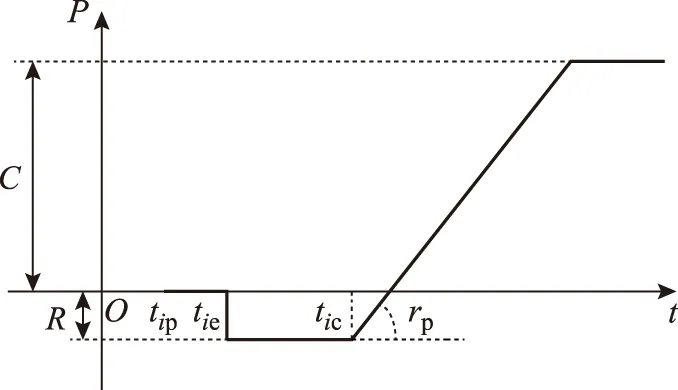
图1 火电机投运出力曲线Fig.1 Curve of thermal unit output

进一步，采用图2阐述多台机组相继启动恢复对整体重构效果的影响。

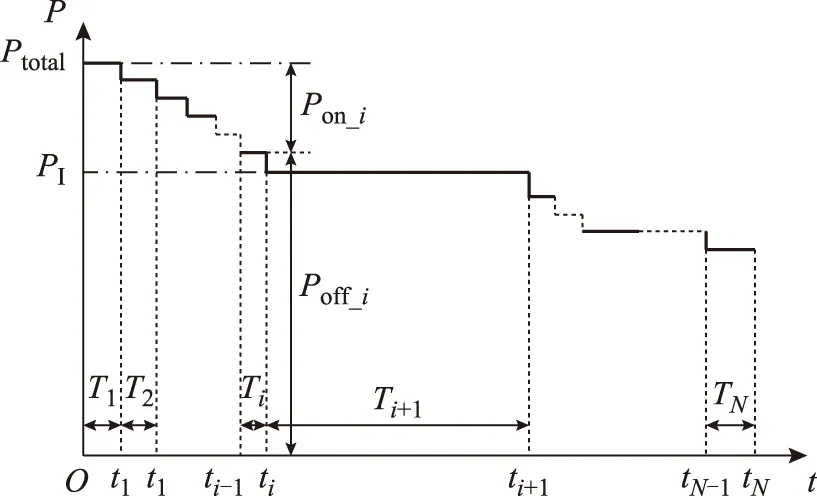
图2 网架重构阶段系统失负荷水平变化曲线Fig.2 Curve of load level change during network reconfiguration

如图2所示，假设大停电发生前系统所带负荷为Ptotal，此即为重构初始时刻的系统失负荷量。随着系统中机组的陆续投运，失负荷量逐步降低。此时，每一失电水平下的持续时间主要由启动相应机组的准备时间决定(图1中的tip～tie时段)。由于在启动机组时还有可能投入少量负荷以稳定运行，所以决定这一时段长度的主要因素是组织相关送电路径的时间长短。考虑到黑启动机组需保留一定旋转备用的要求，在其无法进一步增加出力的情况下，往往需要等待已启动机组并网后，才能进一步持续接入负荷。因此图2中经历了黑启动初期失电水平阶梯状降低的阶段后，会在某一失电水平下(如PI)持续较长时间，这一时段长度主要体现为某一机组的启动时段(图1中的tie～tic时段的一部分)。可以看出，如果某些机组是在这样的时间延迟之后才进入启动准备阶段，由于停机时间的延长，机炉温度和压力的下降会导致其启动时间增长，阻碍机组发电能力的恢复速度，降低重构效率。

综上所述，本文将考虑网架重构过程中机组在启动准备阶段和启动阶段可能的时间迟滞场景，构建能够最大化重构效率，减小失电损失的机组恢复顺序鲁棒优化模型。

2 机组恢复顺序鲁棒优化模型

在对历次大停电事故严重程度的调查中，通常采用失负荷量和停电持续时间来衡量停电的严重程度[16]。从重构的目标来看，为了最大限度地减小失电损失，应该最小化图2中失负荷水平变化曲线和时间轴围成的面积，即电量不足。如果经N个时步完成重构，第i时步的失负荷量和停电持续时间分别为Poff_i和Ti，则重构期间电量不足可表示为

(1)

由前述机组相继启动恢复对整体重构效果影响的分析可知，重构过程由两类时步交织而成，即延时较短的机组准备时步和较长的机组启动时步。因此式(1)可细化为

(2)

式中,NP和NS分别为机组准备和机组启动的时步数。同时，为便于后续建模，将相应时步的失负荷量和停电持续时间的标识符号下标进行了调整。

进一步，为了体现因机组准备和机组启动时间的不确定给重构效果带来的影响，引入服从均匀分布的不确定时长，即

(3)

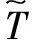
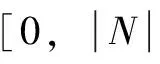
(4)

式中，βP(PP_off,Γ)和βS(PS_off,Γ)分别为火电机组启动准备时段和启动时段的时间迟滞对系统电量不足的影响。二者的表达式相似，现统一进行说明。

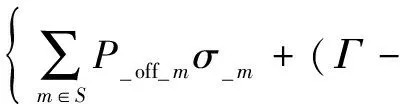
(5)

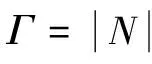
式(4)中，βP(PP_off,Γ)和βS(PS_off,Γ)为非线性变量。为方便计算，现将其进行线性化处理为

(6)

式中，zm为辅助变量。

上述鲁棒优化模型涉及最小最大问题求解，运用对偶理论将式(6)进行等价转换得

(7)

式中，um和v为对偶变换引入的辅助变量。

网架重构是一个复杂的恢复问题，所建立的鲁棒优化模型除了考虑各阶段时间迟滞的不确定约束外还需综合考虑重构过程中的系统功率平衡、旋转备用、机组特性和运行安全等约束条件。现将完整的机组恢复顺序鲁棒优化模型整理如下。

目标函数为

minZ

(8)

鲁棒模型约束为

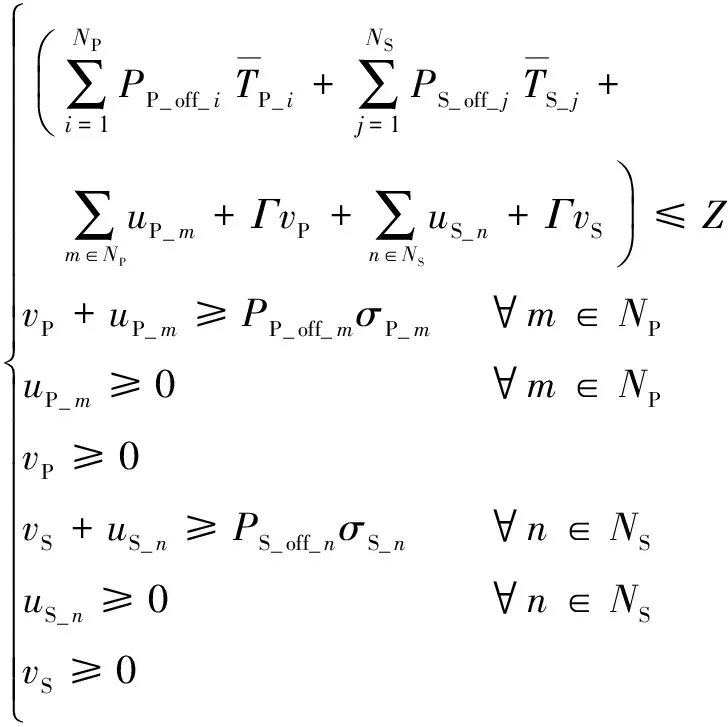
(9)

潮流约束为

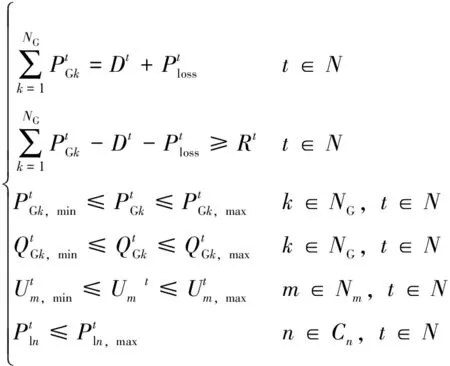
(10)

式中,N为恢复过程总时步数；NG为在启动时限内被启动机组数；Nm为恢复网架包含节点的个数；Cn为组成恢复网架的线路条数；在特定的时步t下PGk、QGk为机组有功、无功出力；D为系统所带负载；Ploss为系统网损；R为旋转备用，Um为节点电压；Pln和Pln,max分别为支路n上流过的有功功率及其允许限值。

3 基于鲁棒优化的机组恢复顺序优化算法

由模型式(1)可知，在确定的机组恢复顺序下，重构期间系统电量不足的求取关键在于获得每个时步下的失负荷量和相应的停电持续时间。

首先，在停电发生前系统所带负荷Ptotal已知的情况下，如果求得某时步下系统累积恢复供电负荷Pon_i，则相应的失负荷量可解。决定当前时步下新增负荷恢复量的因素主要包括：黑启动机组或初期已恢复小系统在满足旋转备用前提下的单次可增发功率限值，待恢复的机组厂用电及需优先恢复的重要负荷量。此外，某时步下的重构阶段网架还需满足相关的运行安全等式及不等式约束。

其次，某时步下停电持续时间的确定主要包括平均时长的求取和偏差波动范围的选择。如前所述，机组准备时步的长度主要由组织相关送电路径的倒闸操作时间决定。根据文献[11]，机组准备时步的平均时长取线路恢复时间的最可能评估值，偏差波动范围取线路恢复时间悲观估计值与最可能评估值之差。对于机组启动时步，受机组类型和停机时间等因素的影响，其平均时长将由火电机组启动及升负荷程序仿真计算所得[15]，偏差波动范围可由现场人员根据机组运行经验估计设定。

对于模型式(9)而言，还需选择鲁棒控制参数Γ。它反映的是鲁棒优化模型的灵活性，调度人员可根据模型中约束被违反的概率Pr来选择相应的鲁棒控制参数。

(11)

综上，可以建立在某一确定机组恢复顺序下最小化重构期间系统电量不足的鲁棒优化模型，这是一线性规划问题，可调用商用软件CPLEX进行求解。为获得计及机组启动过程不确定后，最小化重构期间系统电量不足的机组恢复顺序，本文将上述鲁棒模型的建模与求解与文献[15]的机组恢复顺序全局寻优思路相结合，形成基于鲁棒优化的网架重构机组恢复顺序全局寻优算法。

机组恢复顺序的全局优化是基于交叉粒子群算法求取的。本文以1,2,…,NG表示待恢复机组编号，粒子初始化为NG位随机的机组编号序列。适应度函数是指导粒子群优化算法搜索方向的依据，以最小化系统电量不足为目标适应度函数表述为

f=minF

(12)

由前述为计算电量不足必须按照粒子所代表的机组恢复顺序模拟重构过程，这就涉及到由黑启动电源和初期带电系统为重要系统负荷寻找最佳供电路径的问题。本文采用Floyd算法以折算到同一电压等级下的支路充电电容为权值求取最优供电路径。

综合交叉粒子群全局优化算法与Floyd最短路径算法，以系统失电量最小为目标的机组鲁棒优化流程框图如图3所示。

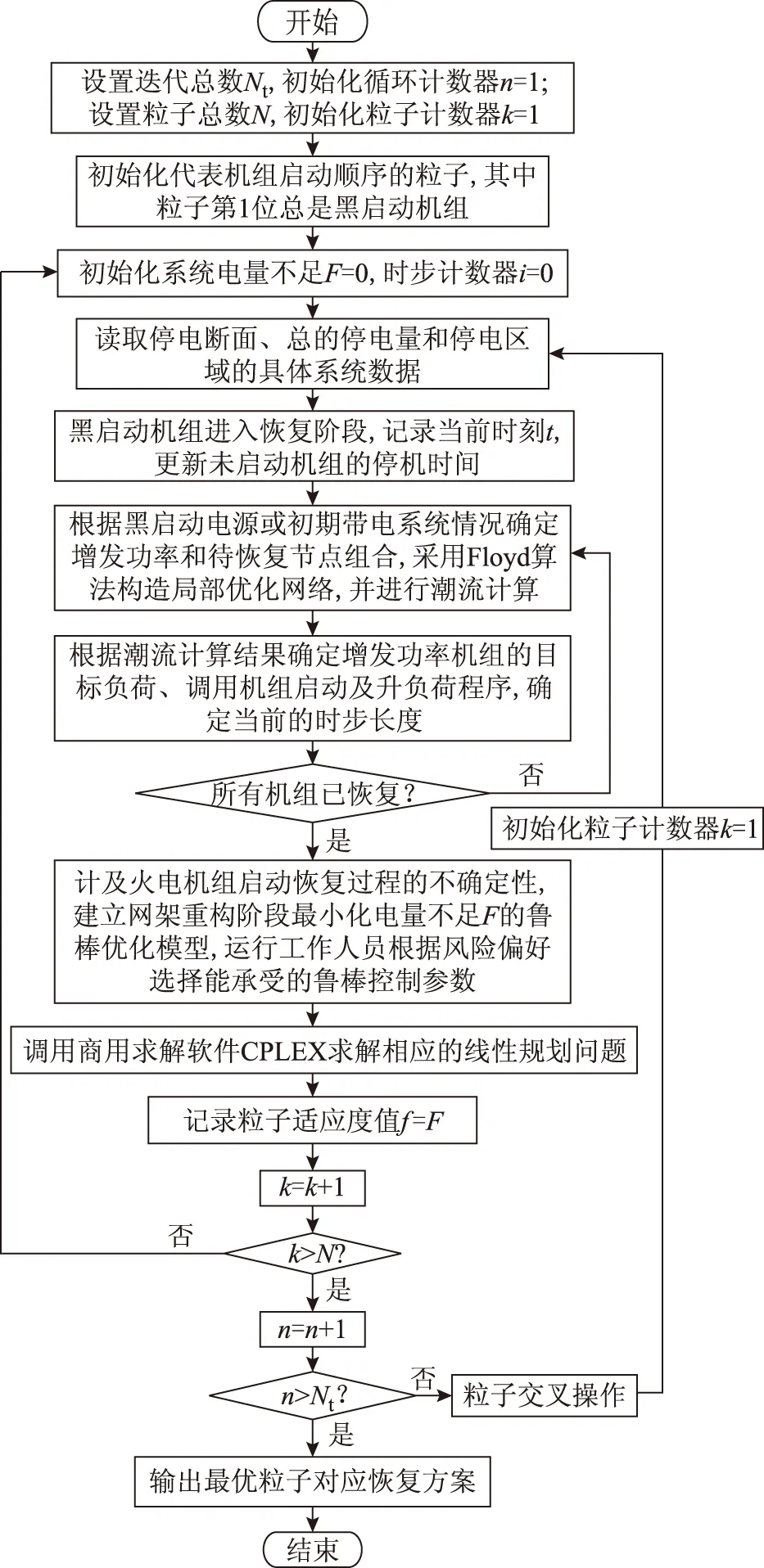
图3 机组恢复顺序优化流程Fig.3 Flow chart of optimal unit’s restoration sequence

4 算例分析

为验证本文所建立的机组恢复顺序鲁棒优化模型的有效性，说明鲁棒控制参数对恢复方案的影响，利用C#、Matlab和CPLEX混合编程进行算法实现。

4.1 新英格兰10机39节点算例

首先选择新英格兰10机39节点系统进行测试，系统结构如图4所示。其中，节点33为水电机组，作为系统的黑启动电源，其他机组均为火电机组。重要负荷及线路相关参数参照文献[11，15]。图4中灰色箭头所示为重要负荷节点。停电前全部机组均正常运行，总出力为3 605.03MW。

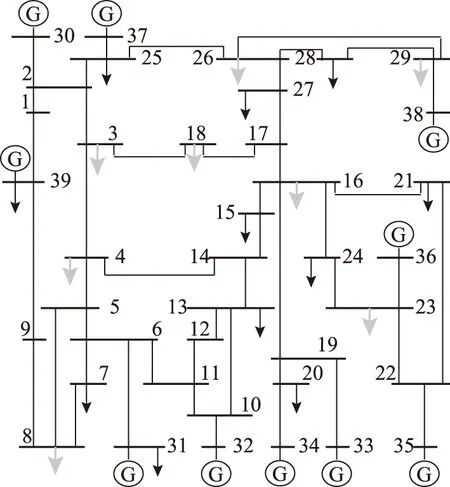
图4 新英格兰10机39节点系统Fig.4 The New England 10-unit 39-bus power system

1)机组恢复顺序鲁棒优化模型的有效性验证。

假设系统全部停电，使用本文方法对机组恢复顺序进行优化。初始化粒子总数N为10，迭代总次数Nt为50。根据图3所示的优化流程可知，基于某一粒子所代表的机组恢复顺序，首先要通过重构过程模拟获得每一时步下的负荷水平和时步长度。其中，时步长度是相应时步的平均时长。为了明确对比重构效果，设定重构阶段计时的终点为恢复所有机组且重要负荷节点的负荷投运比例达到停电前的30%。接下来，需要设置各时步的恢复时间偏差波动范围和鲁棒控制参数Γ，进而建立鲁棒优化模型。机组启动准备时段的时间偏差波动范围取值参照文献[11]，机组启动时段的时间偏差波动范围设置为相应时步平均时长的10%。为了观察鲁棒控制参数Γ所起到的作用，首先考虑两种极端情况，将Γ分别设为0和10，代表所有机组都顺利启动恢复和所有机组均出现恢复延时。经鲁棒优化，这两种场景下的恢复时间分别为10.7 h和11.8 h；重构期间电量不足分别为30 794.2 MW·h和39 790.79 MW· h。整个重构过程的电量不足变化趋势如图5所示。方案1是最理想的恢复场景，各时步的恢复过程均为理想过程，没有出现时间延迟的情况，此时的鲁棒优化模型被简化为确定性优化模型，与文献[16]恢复过程类似，恢复时步较紧凑，能够最小化重构期间的电量不足。而方案2代表了最严重的机组恢复迟滞场景，相应的电量不足是在这种情况下通过优化机组恢复顺序所达到的最低水平。

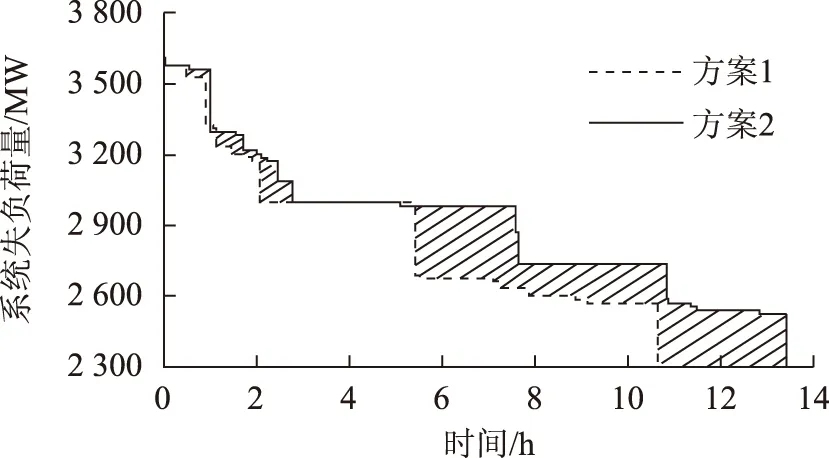
图5 方案1、2电量不足对比Fig.5 Comparison of energy not supplied regarding scheme 1 and 2

根据式(11)，鲁棒控制参数Γ的取值对应一定的模型约束违反概率。相应地，上述两方案违反模型约束的概率分别为62.3%、0%。这意味着，方案1的重构效果虽然理想，但由于不具备鲁棒性，在实际恢复过程中，路径倒闸操作或机组启动并网环节一旦出现延时，失电量增大的可能性非常大，恢复过程的潜在风险较高。恰恰相反，方案2考虑了各时步可能出现的最长延时，代表了最不利恢复场景，实际恢复过程不存在比其更为恶劣的情况，相应的机组恢复顺序能够最大限度抑制各操作环节延时给总体重构效果带来的不利影响，具有较强的鲁棒性。通过上述分析可知，鲁棒控制参数Γ的取值在一定程度上反映了重构方案在恢复效果和运行可靠性之间的权衡或取舍。据此，调度人员可根据实际运行经验，通过选择模型约束的违反概率，进而确定鲁棒控制参数Γ，优化获得可靠性较高且恢复效果可以满足需求的机组恢复顺序。举例来说，调度人员分别取约束违反概率为5%和1%，与之对应的鲁棒控制参数Γ分别取6.1和8.2。利用本文方法对机组恢复顺序进行优化，其恢复效果见表1。为方便比较，将前述两种极端情况下的恢复方案重新编号，一并列于表1中。

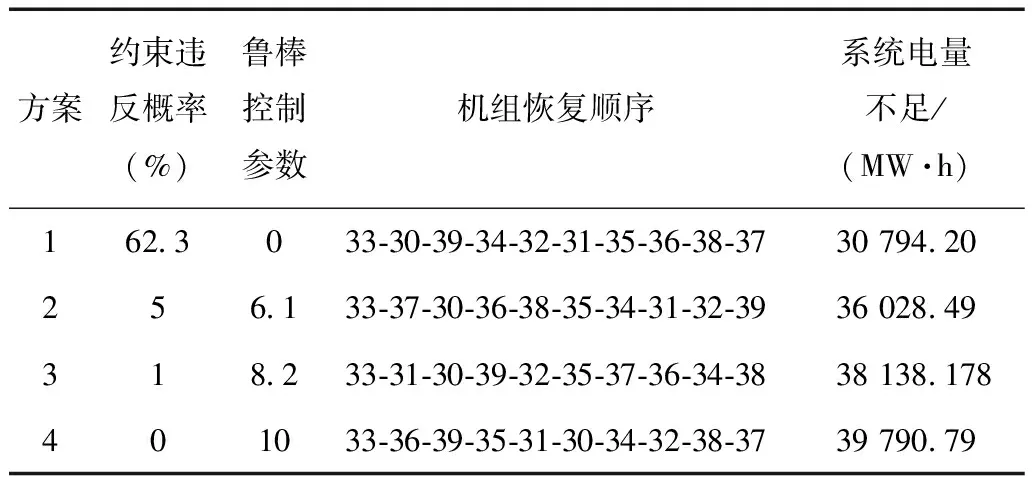
表1 不同鲁棒控制参数系统恢复方案对比

由表1可以看出，随着鲁棒控制参数取值的增大，代表重构效果的系统电量不足逐渐增大，但反映方案操作风险的约束违反概率逐渐减小，即方案的运行可靠性不断提升。

2)鲁棒控制参数对恢复方案的影响分析。

为积极应对大停电，调度人员通常会根据系统实际情况和已有运行经验制定相应的恢复预案，并对发电机启动、线路空载合闸和厂用辅机启动等关键技术问题进行校验，发现其中可能的运行风险并采取措施加以防范。然而，由于调度人员缺少对恢复预案总体恢复效果和运行可靠性的量化评价手段，通常只能凭借经验估计方案顺利投运的可能性，至于哪些投运环节的推迟或延误可能恶化恢复效果的程度，尚无法把握。据此，本文利用CPLEX解决混合整数线性规划的能力，从模型式(6)入手，求解不同时步时间迟滞对重构期间系统电量不足的影响。

仍以前述新英格兰10机39节点系统为例。假设调度人员拟定的机组恢复顺序为33-39-36-37-31-38-35-34-32-30，各时步的时间偏差波动范围设定方法同前。现取理想恢复过程、模型约束违反概率为50%和5%情况形成3个恢复场景，相应的重构过程电量不足分别为30 617.50 MW·h、32 251.28 MW·h和34 528.55 MW·h，变化趋势如图6所示。由于三种场景的机组和路径恢复顺序完全相同，因此各时步对应的系统失负荷量相同，差异仅体现在各时步的恢复时间不尽相同。

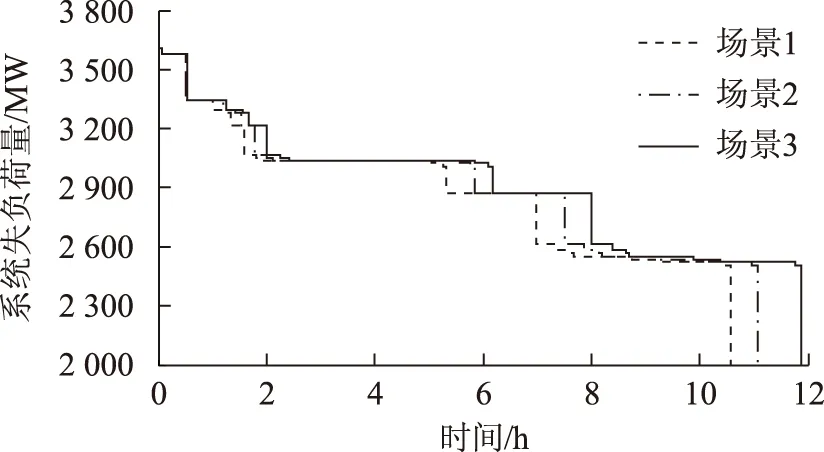
图6 场景1、2、3电量不足对比Fig.6 Comparison of energy not supplied regarding scenario 1 ，2 and 3

针对场景2和场景3，利用CPLEX可解出鲁棒控制参数Γ对各时步恢复时间的影响。Γ相应各时步的取值见表2。其中相应不为0的时步为恢复的关键时步，表中所给出的Γ对各时步的影响表示的是在相应约束违反概率下可能出现的最严重的时间迟滞场景。

现提取场景3中数据，关键时步延时后对恢复效果电量不足的影响与理想恢复情况下该时步电量不足的对比如图7所示。其中，前7个时步为机组启动准备阶段对应关键时步，后7个时步为机组启动阶段对应关键时步。在相应的机组启动准备阶段或启动阶段排序越靠前的时步计及恢复时间不确定性后对电量不足的影响越大，因而在恢复过程中重要等级越高。调度人员根据所能承受的模型中约束违反概率使用本文算法得出恢复过程的关键时步，只需保证关键时步恢复时间在最大偏差极限值内即可保证恢复效果。

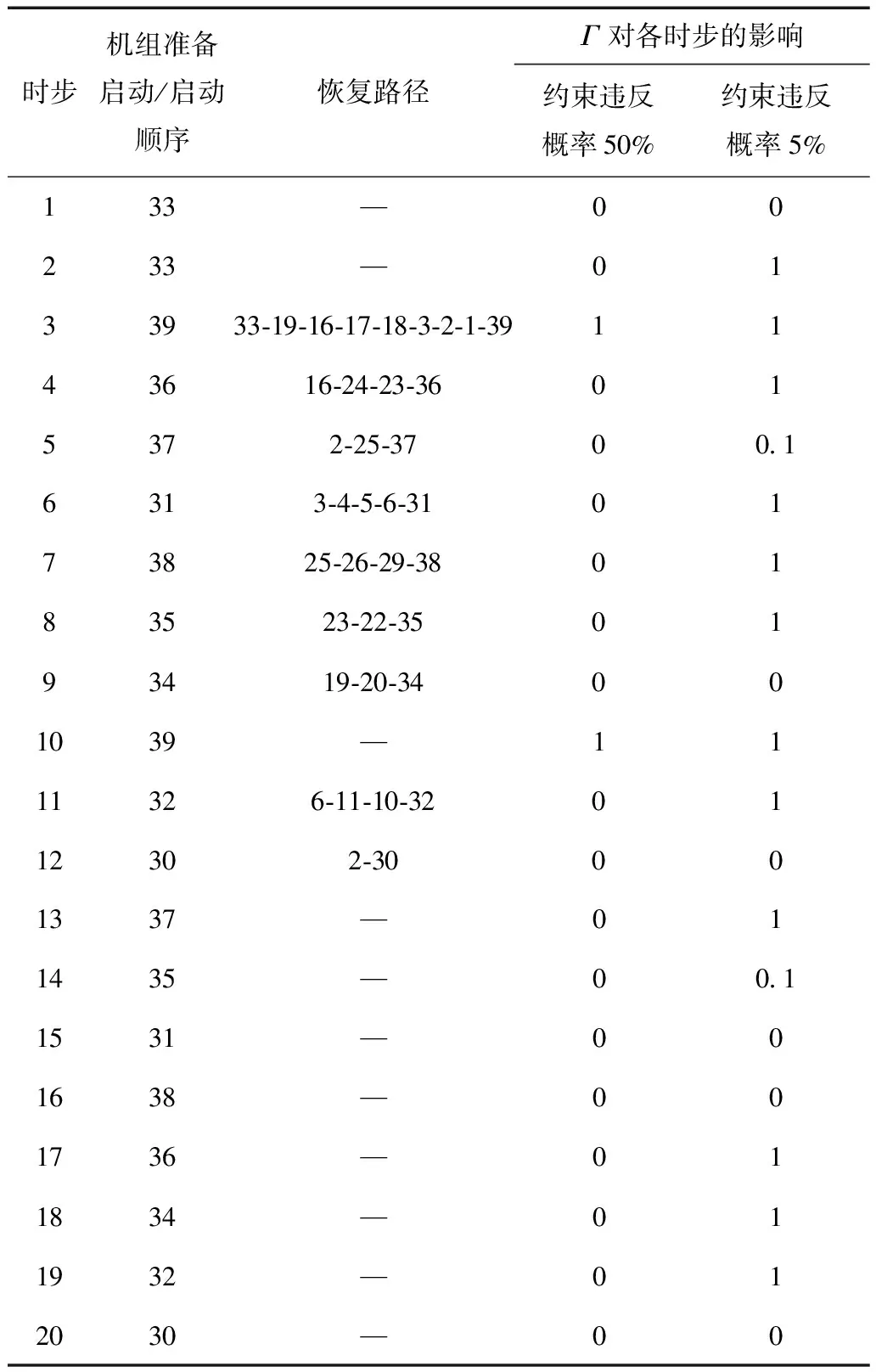
表2 特定机组恢复顺序下鲁棒模型具体恢复过程

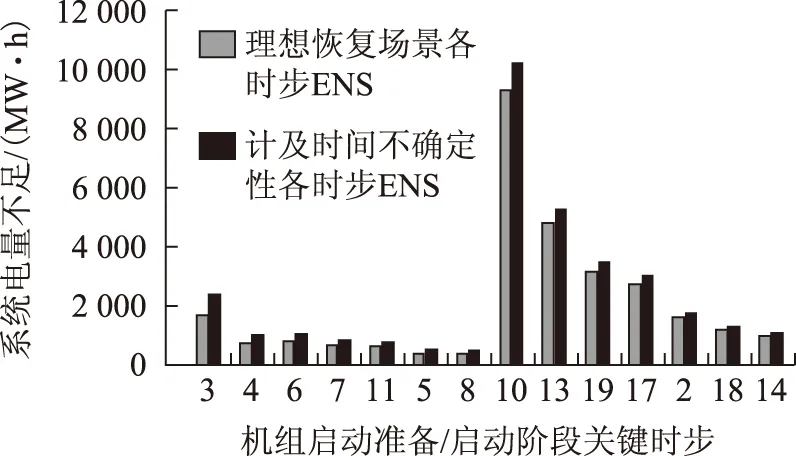
图7 关键时步延时后恢复效果与理想恢复过程对比Fig.7 Comparison of restoration effect between key steps delayed and the ideal process

4.2 某区域电网算例

为了进一步验证本文方法的有效性，进一步选用某区域电网进行仿真验证。经简化后的系统结构如图8 所示。其中WM(G)为黑启动电源，其余机组均为火电机组。

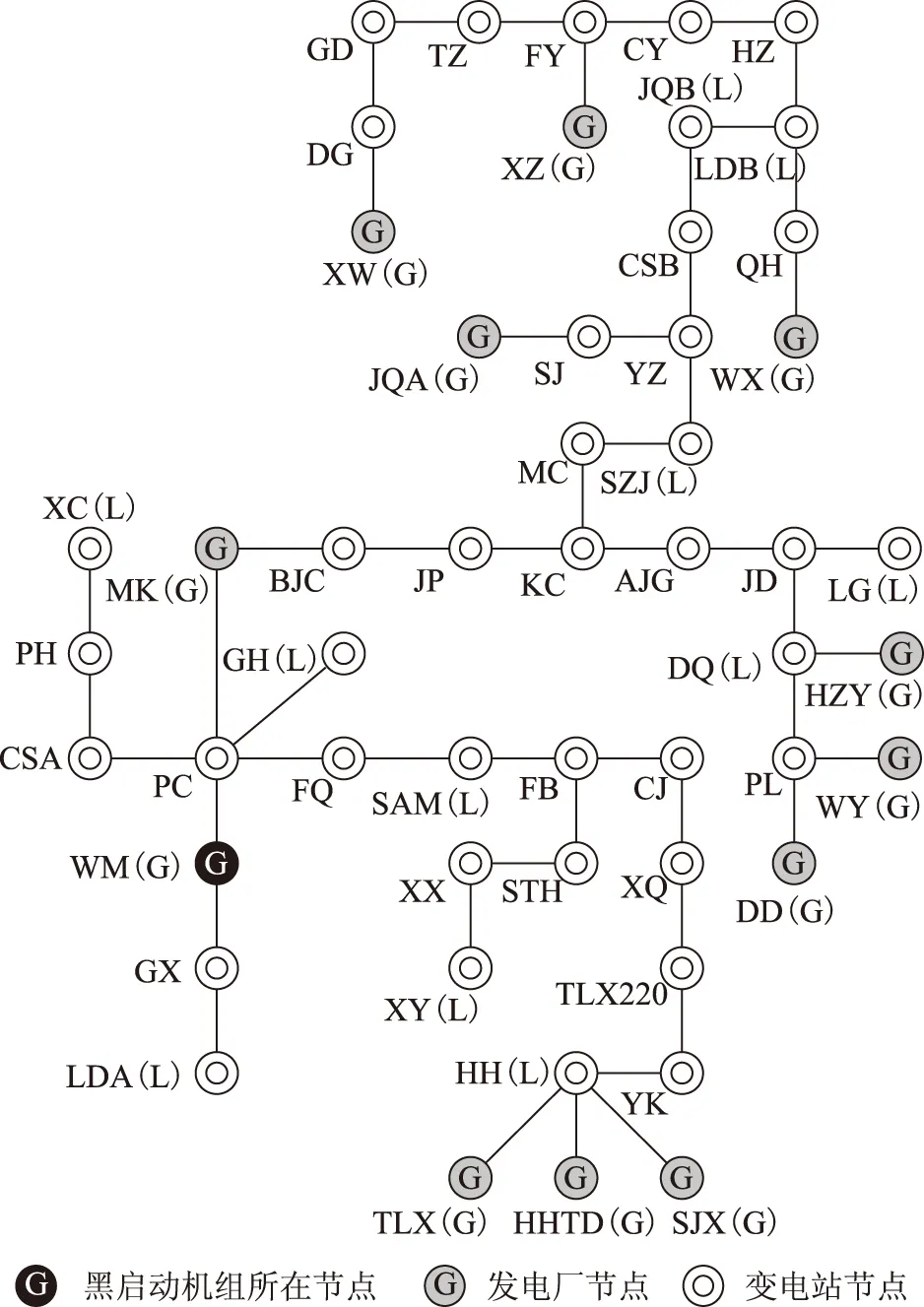
图8 某区域电网系统Fig.8 A region grid power system

本算例的具体恢复过程与相关参数的选取方法同前，此处不再赘述。首先验证不同鲁棒控制参数的取值对恢复效果的影响。

不同鲁棒控制参数系统恢复方案对比见表3，随着方案鲁棒性逐步增强，系统电量不足逐渐增大。因为方案的重构效果和运行可靠性已通过系统电量不足和约束违反概率得到定量描述，从而为运行调度人员根据运行经验和实际恢复需要选择恢复方案提供了更加全面的决策依据。

表3 不同鲁棒控制参数系统恢复方案对比

其次，针对调度运行人员自行拟定的某恢复预案，进一步利用本文方法对具体方案的关键时步进行分析。相应机组恢复顺序设为WM-SJX-MK-XZ-HZY-HHTD-TLX-JQA-DD-WX-WY-XW。为研究不同时步时间迟滞对方案恢复效果的影响，考虑模型中约束违反概率为10%的恢复场景。使用本文方法可以提取出约束违反概率下调度运行人员需要特别注意的关键时步，分别包括机组HZY、XZ、WY、WX、HHTD、TLX的启动准备时步和机组HZY、WY、WX、TLX、XW、WM的启动时步，在实际运行过程中，保证上述关键时步的时间迟滞不超过最大偏差极限即可保证恢复效果。在此场景中，所提取的关键时步延时后对恢复效果的影响与理想情况下恢复效果对比如图9所示。

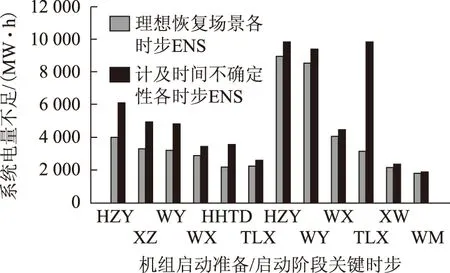
图9 关键时步延时后恢复效果与理想恢复过程对比Fig.9 Comparison of restoration effect between key steps delayed and the ideal process

5 结论

本文计及火电机组启动过程不确定因素对重构效果的影响，以系统电量不足最小为目标来优化大停电后机组的恢复顺序。通过分析，将火电机组的恢复过程分为启动准备阶段和启动阶段两部分，建立考虑不确定性的鲁棒优化模型。调度人员可根据实际运行经验，通过选择模型中约束的违反概率，进而确定鲁棒控制参数Γ，优化获得可靠性较高且恢复效果可以满足需求的机组恢复顺序。本文的方法与以往的网架重构优化方法相比，考虑了网架重构过程中各恢复阶段可能的时间迟滞场景，在既定的机组恢复顺序下运行调度人员可以根据本文算法找出影响恢复过程的关键时步，保证这些时步的恢复时间在最大偏差极限值内即可保证恢复效果。对实际的网架重构过程中机组恢复顺序优化有较好的指导意义。

[1] Fink L H， Lion K L，Liu C C.From generic restoration to specific restoration strategies[J].IEEE Transactions on Power Systems,1995，10(2)：745-752.

[2] Ancona J J.A framework for power system restoration following a major power failure[J].IEEE Transactions on Power Systems，1995，10(3)：1480-1485.

[3] 代文章.电力系统的安全性及防治措施[J].电气技术,2011(12)：85-89. Dai Wenzhang.Power system security and its prevention[J].Electrical Technology，2011(12)：85-89.

[4] 李振坤，周伟杰，钱啸，等.有源配电网孤岛恢复供电及黑启动策略研究[J].电工技术学报，2015，30(21)：67-75. Li Zhenkun，Zhou Weijie，Qian Xiao，et al.Distribution network restoration and black start based on distributed generators[J].Transactions of China Electrotechnical Society，2015，30(21)：67-75.

[5] 顾雪平，王大江，梁海平，等.电力系统扩展黑启动方案动态综合评估[J].电工技术学报，2015，30(3)：44-52. Gu Xueping，Wang Dajiang，Liang Haiping，et al.Dynamic comprehensive assessment of power system extended black-start plans[J].Transactions of China Electrotechnical Society，2015，30(3)：44-52.

[6] 顾雪平，王大江，李少岩，等.电力系统扩展黑启动方案的后效性研究[J].电工技术学报，2015，30(8)：238-246. Gu Xueping，Wang Dajiang，Li Shaoyan，et al.Investigation on aftereffect of power system extended black-start schemes[J].Transactions of China Electrotechnical Society，2015，30(8)：238-246.

[7] 董张卓，焦建林，孙启宏.用层次分析法安排电力系统事故后火电机组恢复的次序[J].电网技术，1997，21(6)：48-51. Dong Zhangzhuo，Jiao Jianlin，Sun Qihong.Arrangement of priority sequence of thermal unit restoration on analytical Hierarchy process model[J].Power System Technology，1997，21(6)：48-51.

[8] 刘强，石立宝，周明，等.电力系统恢复中机组恢复的优化选择方法[J].电工技术学报，2009，24(3)：164-170. Liu Qiang，Shi Libao，Zhou Ming，et al.Optimal strategy for units start-up during power system restoration[J].Transactions of China Electrotechnical Society，2009，24(3)：164-170.

[9] Sun Wei，Liu C C，Zhang Li.Optimal generator start-up strategy for bulk power system restoration[J].IEEE Transactions on Power Systems，2011，26(3)：1357-1366.

[10]曾顺奇，文福栓，薛禹胜，等.计及操作时间不确定性的电力系统网架重构策略优化[J].电力系统自动化，2011，35(23)：16-21. Zeng Shunqi，Wen Fushuan，Xue Yusheng，et al. Optimization of network reconfiguration strategy for power systems considering operating time uncertainty[J].Automation of Electric Power Systems，2011，35(23)：16-21.

[11]孙磊，刘伟佳，林振智，等.计及线路投运风险的电力系统恢复路径优化[J].电力系统自动化，2015，39(23)：68-83. Sun Lei，Liu Weijia，Lin Zhenzhi，et al.Determination of optimal restoration paths for power systems considering failure risk of restoring transmission lines[J].Automation of Electric Power Systems，2015，39(23)：68-83.

[12]王江宇，刘艳.基于重构方案线路投运风险最小的机组恢复顺序优化[J].电力系统保护与控制，2016，44(11)：68-75. Wang Jiangyu，Liu Yan.Optimization of unit’s restora-tion sequence based on minimizing of lines’ restoration risk corresponding to reconfiguration scheme[J].Power System Protection and Control，2016，44(11)：68-75.

[13]张雪丽，梁海平，朱涛，等.基于模糊机会约束规划的电力系统网架重构优化[J].电力系统自动化，2015，39(14)：68-74. Zhang Xueli，Liang Haiping，Zhu Tao，et al.Optimization of power network reconfiguration based on fuzzy chance constrained programming[J].Automation of Electric Power Systems，2015，39(14)：68-74.

[14]刘艳，张凡，顾雪平.大停电后的机组投运风险评估[J].中国电机工程学报，2013，33(31)：106-112. Liu Yan，Zhang Fan，Gu Xueping.Risk assessment for restoring units following large-scale blackout[J].Proceedings of the CSEE，2013，33(31)：106-112.

[15]刘艳，张华.基于失电风险最小的机组恢复顺序优化方法[J].电力系统自动化，2015，39(14)：46:53. Liu Yan，Zhang Hua.Optimization of units’ restoration sequence based on minimizing risk of electrical energy loss[J].Automation of Electric Power Systems，2015，39(14)：46-53.

[16]Adibi M M， Martins N.Power system restoration dynamics issues[C]//Power and Energy Society General Meeting，2008：1-8.

[17]艾小猛，韩杏宁，文劲宇，等.考虑风电爬坡时间的鲁棒机组组合 [J].电工技术学报，2015，30(24)：188-195. Ai Xiaomeng，Han Xingning，Wen Jinyu，et al. Robust unit commitment considering wind power ramp events[J].Transactions of China Electrotechnical Society，2015，30(24)：188-195.

[18]梅生伟，郭文涛，王莹莹，等.一类电力系统鲁棒优化问题的博弈模型及应用实例[J].中国电机工程学报，2013，33(19)：47-56. Mei Shengwei，Guo Wentao，Wang Yingying，et al. A game model for robust optimization of power systems and its application[J].Proceedings of the CSEE，2013，33(19)：47-56.

[19]Bertsimas D, Thiele A. Robust and data-driven optimization modern decision making under uncertainty[EB/OL].[2012-10-15].http://web.mit.edu/dbertsim/www/papers/Robust%20Optimization/Robust%20and%20data-driven%20optimization-%20 modern%20decision-making%20under%20uncertainty.pdf.

[20]Bertsimas D， Sim M.The price of robustness[J].Operations Research，2004，52(1)：35-53.

(编辑 赫蕾)

Optimization of Units’ Restoration Sequence during Network Reconfiguration Process Based on Robust Optimization

JiaoJieLiuYan

(School of Electrical and Electronic Engineering North China Electric Power University Baoding 071003 China)

Current power systems mainly consist of thermal units, the length of units’ recovery time after blackout determines the effect of network reconfiguration significantly. In response to this problem, aiming at the possible delay when units prepare to start and start up. In this paper, the robust optimization model for units’ restoration sequence is set up which considers uncertain units start time, and treat insufficient electricity as optimization goal during minimum reconfiguration period. Then, crossover particle swarm algorithm and CPLEX optimization solution are combined to solve this model. Based on this, a units’ recovery sequence which can quantitative characterization effort of recovery and operation reliability can be

. Providing the reference for dispatcher to cope with the worst possible restore hysteretic scene. Further, for the proposed units’ recovery sequence given by dispatcher, they can get the probability of successful implementation estimated by operating experience and obtained the key steps by CPLEX to ensure recovery effect. The outcome of its application on the New England 10-unit 39-bus power system and a region grid indicate the validity of the method proposed.

Network reconfiguration, unit recovery, uncertain time of thermal units startup, robust optimization

国家自然科学基金资助项目(51277076,51677071)。

2016-07-06 改稿日期2016-10-09

TM732

焦 洁 女，1991年生，硕士研究生，研究方向为电力系统安全防御与恢复控制。

E-mail：jiejiedewu@163.com(通信作者)

刘 艳 女，1973年生，博士，教授，研究方向为电力系统安全防御与恢复技术智能技术在电力系统中的应用、状态检修等。

E-mail：bd_ly@263.net