基于投影能量函数和Pin-SVM的电力系统暂态稳定评估

陈厚合 王长江 姜 涛 李 雪 李国庆

(东北电力大学电气工程学院 吉林 132012)



基于投影能量函数和Pin-SVM的电力系统暂态稳定评估

陈厚合 王长江 姜 涛 李 雪 李国庆

(东北电力大学电气工程学院 吉林 132012)

提出一种基于Pin-SVM的电力系统暂态稳定评估方法。首先，采用系统指标(如平均机械功率、初始加速度和系统冲击等)和投影能量函数指标(如投影角速度、投影角加速度和投影动能PKE)构建暂态稳定指标的原始特征集，通过最大相关最小冗余特征选择方法对暂态指标集进行特征压缩，寻找对电网暂态变化敏感度高的特征子集；然后，基于Pin-SVM思想将特征子集映射到高维空间，实现非线性暂态稳定评估问题的线性转换，进而引入分位数改变系统稳定类与不稳定类之间的最近点位置，将暂态稳定分类问题转换为在Pin-SVM中寻找最优分位数距离问题，以减小边界干扰样本的影响，提高电力系统暂态评估方法的评估准确率和稳定性。最后，以IEEE-39节点系统、IEEE-145节点系统和某实际算例进行仿真计算，计算结果验证了该方法的有效性和准确性。

投影能量函数Pin-SVM广域测量系统 暂态稳定评估

0 引言

暂态稳定评估(Transient Stability Assessment，TSA)是电力系统安全稳定分析的重要组成部分[1，2]。随着电力系统不断发展，区域电网互联规模不断扩大，电力系统正面临更多的安全稳定运行风险，为避免类似美加和西欧大停电事故的重演[3，4]，寻求准确、稳定的电力系统暂态稳定评估方法具有重要意义[5]。

目前，电力系统暂态稳定评估的方法主要有3类：①时域仿真法[6]，它是通过求取系统状态变量和代数量随时间的变化曲线，根据发电机的转子摇摆曲线来判别系统的稳定性，是最早的暂态稳定分析方法，该方法具有很高的准确性，可作为其他暂态稳定分析方法的参考，但时域仿真法需求解大量代数-非线性方程，计算量巨大，计算速度较慢，难以满足电力系统实时评估的需要[7];②直接法[8]，又称李雅普诺夫直接法，该方法是从能量的角度来判断系统的稳定性，采用暂态动能和暂态势能等指标来评估系统的暂态稳定状态，能够给出系统的暂态稳定裕度，确定系统失稳趋势，但受系统非线性时变因素的影响，该方法所确定的极限能量具有一定误差[9]，且系统拓扑改变后需重新构建能量函数，鲁棒性较差；③人工智能法[10-13]，它是通过离线训练得到系统状态变量与暂态稳定性之间的映射关系，将映射关系用于电力系统实时暂态稳定评估，具有精度高、耗时短、维度低且容易生成决策树等优点[14-16]，在电力系统实时评估中得到广泛应用[17，18]。

人工智能方法中以统计学原理为基础的支持向量机(Support Vector Machine，SVM)算法已在电力系统暂态稳定评估中得到广泛应用[2]，但该方法在实际应用中存在输入特征构建与选取及分类器构建的难题仍需改善[17，18]。较多的输入特征可能包含与稳定性指标无关的特征，特征之间的冗余使得模型训练时间长、权值收敛困难及分类性能不理想；而能量函数指标与系统稳定性强相关，少量指标即可表征系统的稳定状态。因此，本文将直接法的暂态动能等指标作为人工智能方法的样本特征，采用最大相关最小冗余(maximal Relevance and Minimal Redundancy，mRMR)特征选择方法对系统指标和投影能量函数指标组成的原始特征集进行特征压缩，可在有效降低特征空间维度的同时增强评估准确率。在分类器的构建方面，文献[19]提出用Pinball损失作为支持向量机的损失函数，可提高SVM评估的稳定性、敏感性和鲁棒性，文献[20]把Pinball损失函数用于Pegasos算法，并讨论其在收敛速度、计算时间和内存成本的优势。由文献[19，20] 可知，Pin-SVM(Support Vector Machine with Pinball loss)相比其他机器学习算法，具有更高的准确率，对边界干扰样本不敏感，评估稳定性强。鉴于现有电力系统暂态稳定评估方法在评估准确率和稳定性上仍需改善的现状，本文将Pin-SVM算法应用在电力系统暂态稳定评估，改善SVM分类器的评估准确率和稳定性。

针对输入特征构建与选取及分类器构建问题，本文利用获得系统的响应轨迹数据，构建由系统指标和投影能量函数指标组成的原始特征集，采用最大相关最小冗余特征选择方法进行特征压缩，找出对电网动态变化敏感度高的特征子集，并将样本集映射到高维空间。用Pin-SVM进行故障筛选和快速暂态稳定判别，将分类问题转换为寻找最优分位数距离问题，通过拓扑搜索方法求取最优解，从而实现故障筛选和快速暂态稳定判别。最后，以IEEE-39节点系统、IEEE-145节点系统和实际电网为例进行仿真分析，验证了本文所提方法的有效性和准确性。

1 Pin-SVM支持向量机

1.1 Pin-SVM的数学模型

Pin-SVM的数学模型为[19]

(1)

式中，m为样本总数；n为样本空间维数；xi为样本空间矢量，xi∈Rn；yi为样本类别标志，yi∈{-1，1}；w和b分别为最优超平面的法矢量和偏差量；C为惩罚参数(表征对误差的精度要求)。Pin-SVM的损失函数Lτ为

(2)

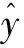
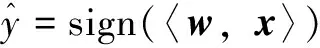
(3)

为将Pin-SVM模型应用到非线性分类问题中，特引入核函数K(xi·xj)。

K(xi·xj)=φ(xi)φ(xj)

(4)

式中，φ为从Rn到Hilbert空间的映射，将样本空间从低维空间映射到高维空间，进而将非线性分类问题转换为线性分类问题。

引入非线性映射φ(x)后的Pin-SVM数学模型为

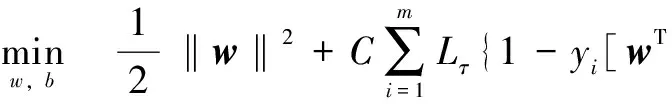
(5)

在此分类器中加入松弛变量ξi(ξi>0)后的等效模型为

(6)

相比C-SVM，Pin-SVM评估性能的优越性体现在所用的损失函数不同：C-SVM的损失函数为L(u)=max{0，u}，用两类之间的最近点来确定两类之间的最大距离；Pin-SVM改变了两类之间最大距离的定义，通过分位数τ改变两类之间最近点的位置来确定两类之间的最大距离，减弱边界干扰样本对评估稳定性的影响。

1.2 边界干扰样本的敏感性分析

Pin-SVM改善评估稳定性的原因可通过线性分类器进行解释说明，定义通用的符号函数sgnτ(u)为

(7)

sgnτ(u)是Lτ(u)的子梯度，Pin-SVM可以写为

(8)

式中，0为u=0时的向量，用符号函数将样本集分成3部分，如式(9)所示。

(9)

(10)

Pin-SVM和C-SVM的评估稳定性和不同τ值下的边界超平面函数，可通过图1的线性分类器进行解释说明。两类样本分别服从U(μ1，Σ)和U(μ2，Σ)的高斯分布，其中μ1=[-0.8，-2]，μ2=[0.8，2]，Σ=[0.2 0；0 2]。图1中的两组样本分别用五角星和乘号代表稳定类和不稳定类。

图1 C-SVM和Pin-SVM分类情况Fig.1 Classification of C-SVM and Pin-SVM

首先，通过C-SVM法找到边界函数〈w,x〉=0，使〈w,x〉=±1之间具有最大的边界距离，并使所有函数都满足y〈w,x〉≥1。图1a、图1b中，〈w,x〉等于-1、0和1分别用单点划线、虚线和双点划线表示，支持向量点用方框表示。图1b给出同分布样本集的C-SVM分类情况。由图1a和图1b可以看出C-SVM受边界干扰样本的影响明显，同分布样本集的边界函数差异很大。

2 投影能量函数

电力系统中描述n台发电机相对于系统惯性中心COI的归一化转子运动方程为[21]

(11)

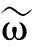
COI坐标系下的角度、角速度和加速功率为

(12)

2.1 投影能量函数的数学模型

文献[22]定义了描述电力系统中发电机功角摆开程度的电力系统角半径R，如式(13)所示。

(13)

在此基础上，定义基于角半径R的伴随系统[23，24]，其数学模型为

(14)

式中，ωθ、αs分别为伴随系统的投影角速度和投影角加速度。

定义投影动能(ProjectionKineticEnergy，PKE)为伴随系统在t时刻的动能[23]。

(15)

2.2 投影能量函数的物理意义

图2为投影能量函数的物理意义示意图。图2a为9节点系统构成的三维θ角度空间，其坐标原点O为发电机角的COI，t时刻电力系统在状态轨迹Tr的位置用质点A表示。如图2b所示，将全部发电机在角度空间中的运动轨迹变换为单位质点A相对于原点O的前后运动，射线OA可定义为旋转一维坐标轴，并随质点A运动。式(13)定义的角半径R描述了质点A在旋转一维坐标轴的位置，式(16)定义的ωθ和αs描述了质点A在旋转一维坐标轴上的运动。

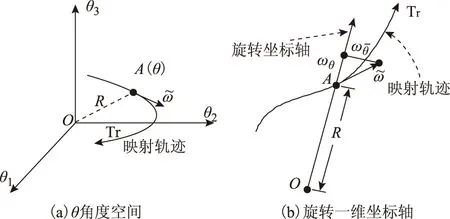
图2 三维θ角度空间与旋转一维坐标轴Fig.2 Three dimension θ angle space and rotating one-dimensional coordinate axis

由上述定义可知，投影角速度ωθ表征系统相对于惯性中心的位置，投影角加速度αs表征发电机组相对于惯性中心的失稳趋势，投影动能PKE描述系统某时刻发电机组的失稳趋势。这三项指标可以有效表征系统的运行稳定状态，将这三项指标加入到Pin-SVM的原始特征集中，可丰富样本集特征，减少冗余信息。

3 基于Pin-SVM的暂态稳定评估

3.1 原始特征集构建

同步相量测量单元可连续不断地监视和测量发电机的功角、各母线电压和电流的幅值、相角。本文在文献[25]的基础上构建原始特征集，通过最大相关最小冗余(mRMR)特征选择方法进行特征压缩，得到与电力系统暂态稳定特性强相关的16维特征集，见表1。

系统指标由X1～X12维特征构成，包含故障初始时刻t0和故障切除时刻tcl的系统特征。投影能量函数指标由2.2节所述的X13～X16维特征构成，该特征由故障初始时刻t0的投影能量函数角加速度、故障切除时刻tcl的投影能量函数角速度、角加速度和投影动能PKE构成。然后，将原始特征集随机分为训练集和测试集，引入核函数将样本集映射到高维空间，将非线性分类转换为线性分类问题，用Pin-SVM进行暂态稳定评估。

表1 数据集的输入特征量

3.2 电力系统暂态稳定评估

首先，对核函数和参数进行设置，不同核函数对算法评估精度和稳定性的影响不同，因此核函数的选择和参数的设置具有重要意义。

其次，将之前获得的训练集用Pin-SVM进行训练，选择合适的τ值，使评估模型具有最好的评估性能。

最后，将测试集输入训练模型，快速得到系统的稳定状态，针对实际电力系统的故障类型，依据其特征变量相对于各类的隶属度将故障划归到某一类。当分类为不稳定类，则认为该故障为严重故障；反之，则认为该故障为不严重故障。在故障筛选和稳定评估完成的同时可得到评价指标。

3.3 评价指标

1)准确率指标。

准确率指标为正确预测数和预测总数的比。Tij表示实际类标号为i但被预测为j的记录数，则准确率A为

(16)

2)Kappa统计值指标。

由于单独评判准确率会存在一定的偶然性，考虑用Kappa来衡量一个数据集的预测分类和实际分类之间的一致性情况。

K= [(T11+T00)(T11+T10+T01+T00)-

(T00+T01)(T00+T10)-(T11+T10)·

(T11+T01)]/[(T11+T10+T01+T00)2-

(T00+T01)(T00+T10)-(T11+T10)(T11+T01)]

(17)

3)ROC曲线指标。

ROC曲线由命中率(TruePositiveRate，TPR)和误报率(FalsePositiveRate，FPR)构成，以TPR作为Y轴，FPR作为X轴。

(18)

(19)

因此系统的综合评价指标为

(20)

3.4 暂态稳定评估流程

依据上述方法，本文所提的系统暂态稳定评估流程分为两步：①原始特征集构建，用mRMR对系统指标和投影能量函数指标组成的原始特征集进行特征压缩，搜索最优特征集，将最优特征集映射到高维空间，分成训练集和测试集；②基于Pin-SVM的电力系统暂态稳定评估，用Pin-SVM对训练集进行离线训练，生成评估模型，并计算在线评价指标值。整体评估流程如图3所示。

图3 暂态稳定评估流程图Fig.3 Flow chart of transient stability assessment

4 算例分析

为验证本文所提方法的有效性和准确性，本文分别以IEEE-39节点系统和IEEE-145节点系统为例进行仿真分析，验证所提方法的准确性；然后，将本文方法应用到某实际电网以验证其有效性。

4.1 IEEE-39节点系统

该系统由10台发电机、39条母线和46条线路组成，节点39所连发电机为等值机，基准功率为100 MV·A，基准电压为345 kV。系统详细参数见文献[26]。

4.1.1 原始样本集构造

通过DSP-BPA进行电力系统仿真计算获得潮流数据和稳定数据。负荷水平有7种(85%、90%、95%、100%、105%、110%和115%)，并设置相应的发电机出力。发电机模型采用4阶模型，各发电机的励磁系统均为IEEE-DC1励磁模型，负荷为恒阻抗负荷，故障类型为三相短路，故障开始时刻为0.1 s，故障清除时刻为0.3 s，故障位置设置在线路的0%、40%、80%处。采用所有发电机的相对功角差最大值Δδmax为暂态稳定与否判据(Δδmax≥360°系统失稳，Δδmax<360°系统稳定)。共获得800个样本，随机选取400个作为训练集构造在线训练模型，其余作为测试集进行在线暂态稳定评估获得在线评价指标。

4.1.2 暂态稳定评估性能分析

1)Pin-SVM的准确性分析。使用4种分类器进行暂态稳定评估，包括C-SVM、nu-SVM、最小二乘支持向量机(LeastSquaresSupportVeotorMachine，LSSVM)和Pin-VSM。在计算过程中，将32作为C的默认值[27]，并采用径向基核函数(Radial Basis Function，RBF)作为默认核函数。τ=0.5时，4种分类器的评价指标见表2。

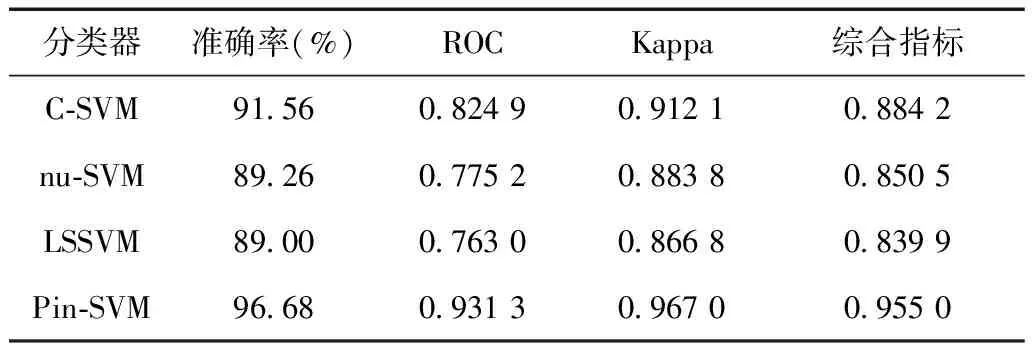
表2 4种分类器的评价指标

图4为4种分类器评价指标图，通过对比准确率指标、ROC指标、Kappa指标，可以发现Pin-SVM的综合评价指标值为0.955 0，高于其他3种分类器，因此Pin-SVM能够保证分类器具有较高的评估精度。

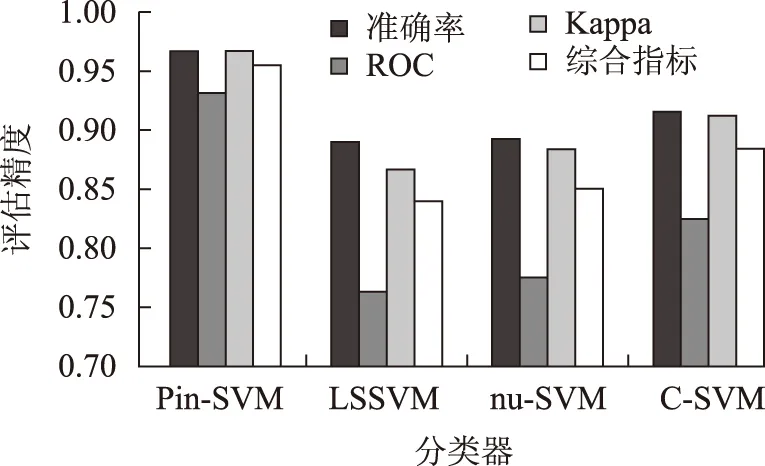
图4 4种分类器的评价指标Fig.4 Evaluation index of four types of SVM

考虑不同τ值对Pin-SVM评估精度的影响，在计算过程中，默认C值为32，并采用径向基核函数(RBF)作为默认核函数。

图5为不同τ值下Pin-SVM的评价指标情况，当τ=0.3时的评估精度最高达到0.978 6，在τ=0.5时的综合评价指标为0.955也高于表2中其他3种分类器的评估精度，满足实际工程需要。随着τ值的增加，评估精度能始终保持在0.958左右，变化幅度很小。因此Pin-SVM的评估性能较现有分类器性能优越。

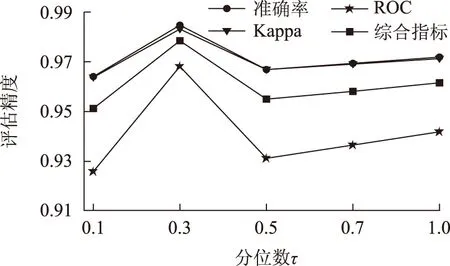
图5 IEEE-39节点系统不同τ值的评价指标Fig.5 IEEE 39-bus system evaluation indexes with different τ values

2)Pin-SVM的稳定性分析。在上述生成的训练和测试样本中加入干扰信号，分析Pin-SVM的暂态稳定评估稳定性。测试集和训练集中加入相同的故障信号，服从U(μ，Σ)的高斯分布，均值为0，方差λ分别取0、0.1、0.5、1时的评估情况见表3。

选择RBF作为Pin-SVM和C-SVM的默认核函数，默认C值为32。随机选取20组同分布干扰信号，评估准确率均值和标准差表示不同τ值和协方差λ对应的评估准确率。由表3可知，协方差λ=0时，Pin-SVM方法各τ值情况和C-SVM方法的系统评估精度不受影响；当协方差λ=0.1时Pin-SVM和C-SVM的评估精度都有所影响，τ=0.1时的平均准确率最高为95.65，τ=0.3和τ=0.4时的平均准确率最低为94.99也高于C-SVM的平均准确率91.30，且τ=0.2时的标准差最小为±0.66，τ=0.4时的标准差最大为

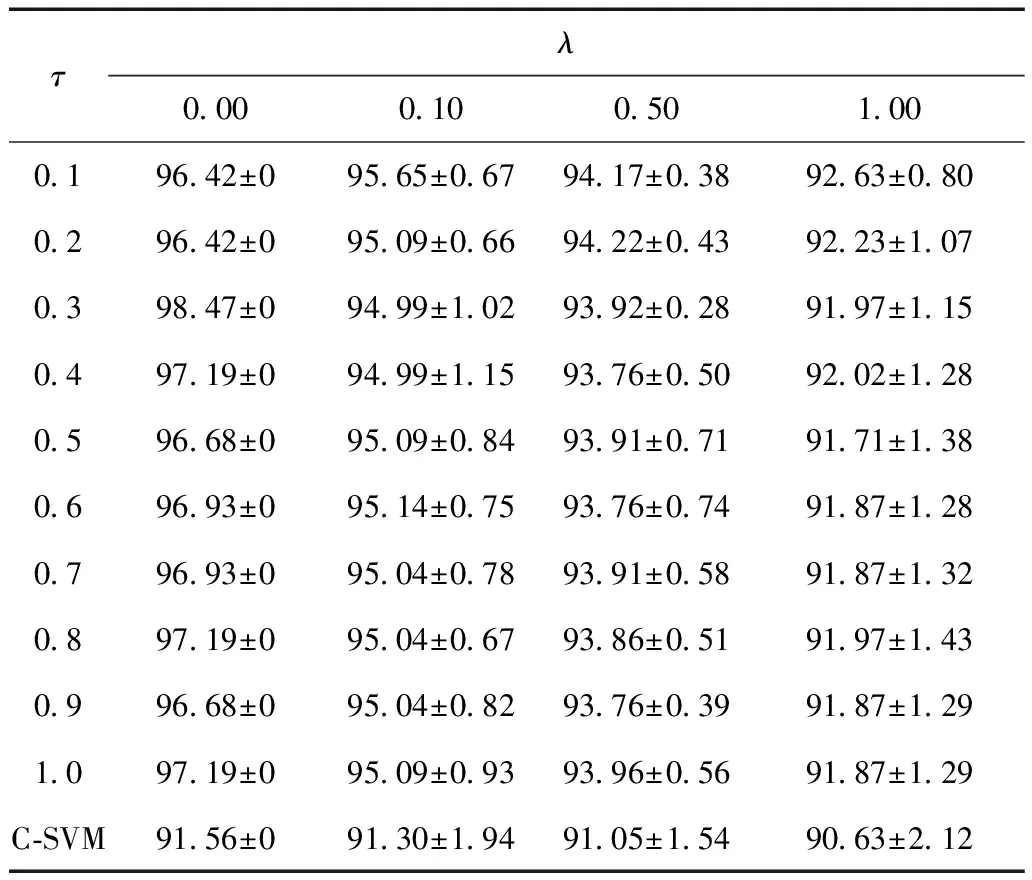
表3 IEEE-39节点系统的评估结果

±1.15也低于C-SVM的标准差±1.94；当协方差λ=0.5、1.0时Pin-SVM和C-SVM抗干扰情况类似。Pin-SVM的最低平均准确率高于C-SVM，最高标准差低于C-SVM。因此Pin-SVM可以改善系统评估稳定性和准确率，受边界干扰样本的影响弱。

3)核函数分析。考虑多项式核函数(Polynomial)、线性核函数(Linear)和径向基核函数(RBF)对Pin-SVM算法的影响，默认C值为32。

图6为3种不同类型核函数的Pin-SVM评价指标，采用径向基核函数具有最高的综合评价指标，线性核函数的综合评价指标最小，但也高于表2中nu-SVM、LS-SVM分类器的综合评价指标，较C-SVM分类器的综合评价指标略低，因此选择径向基核函数作为Pin-SVM的核函数。

图6 3种核函数的Pin-SVM评价指标Fig.6 Pin-SVM evaluation index with three kinds kernel function

4.2 IEEE-145测试系统

4.2.1 原始样本集构造

IEEE-145测试系统共有50台发电机、145条母线、453条线路[26]，节点139所连发电机为平衡机，基准功率为100 MV·A，基准电压为100 kV。发电机采用经典模型，负荷采用恒阻抗模型，故障类型为三相短路，故障开始时刻是0.1 s，故障清除时刻为0.2 s，负荷水平有8种(80%、85%、90%、95%、100%、105%、110%、115%)，并设置相应发电机出力。随机设置50个故障位置，用DSP-BPA进行电力系统仿真计算来获得相应数据。共获得400个样本，随机选取200个作为训练集构造在线训练模型，其余作为测试集进行在线暂态稳定评估获得在线评价指标。暂态稳定判据同10机39节点算例。

4.2.2 暂态稳定评估性能分析

1)Pin-SVM的准确性分析。当τ=0.5时使用4种不同分类器进行电力系统暂态稳定评估，评价指标见表4。

表4 4种分类器的评价指标

由表4可知，Pin-SVM较其他分类器有较高的评估精度，综合评价指标可达到0.979 2。

图7为不同τ值下Pin-SVM的评价指标。当τ=0.1时，具有最高的评估精度0.985 7，随着τ值增加，评估精度略有下降并能保持在0.979 2不变，可见合理选择τ可以改善系统的评估稳定性，保证较高的评估精度。

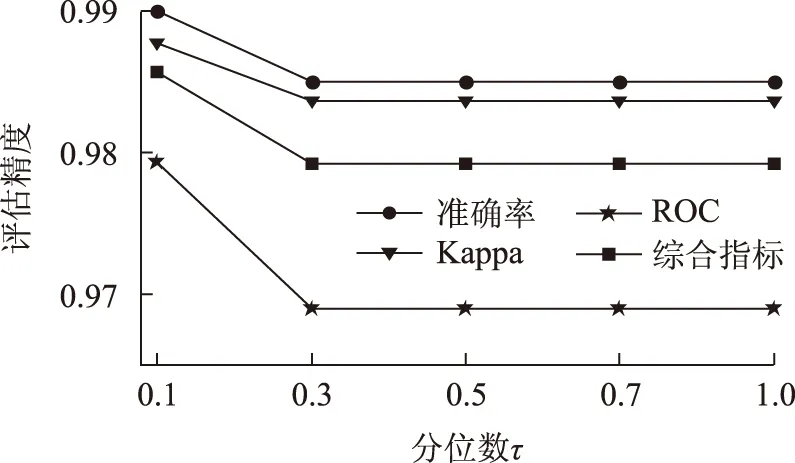
图7 IEEE-145系统不同τ值的评价指标Fig.7 IEEE 145-bus system evaluation indexes with different τ

2)Pin-SVM的稳定性分析。故障信号和IEEE 39节点系统相同，每种情况随机选取20组同分布干扰信号的评估准确率均值和标准差，结果见表5。

由表5可知，本文所提方法在IEEE-145测试系统中的平均准确率高于C-SVM，标准差小于C-SVM。因此，Pin-SVM在IEEE-145系统中同样可以改善评估稳定性和准确率。

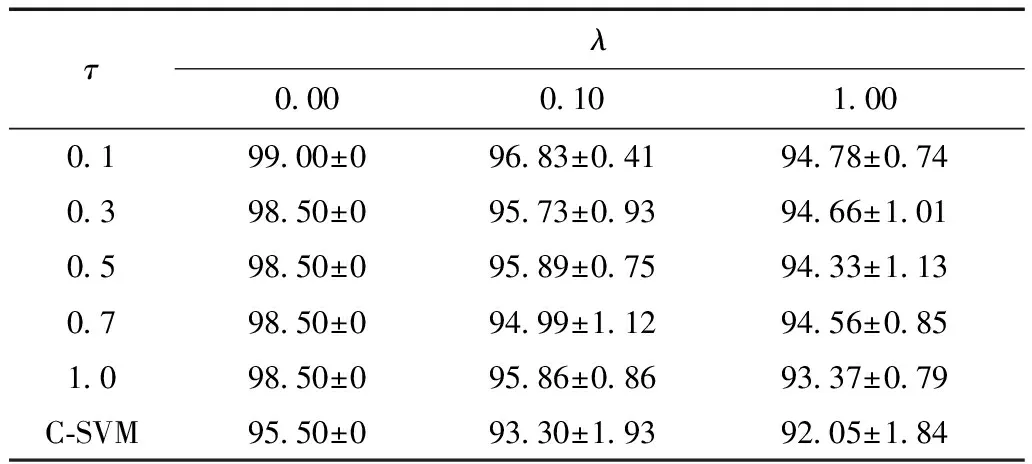
表5 IEEE-145节点系统的评估结果

4.3 我国某实际电网算例

本节进一步将本文所提算法应用到某实际电网算例，如图8所示。故障类型为三相短路，故障线路均为500 kV线路，故障开始时刻是0.2 s，故障清除时刻为0.4 s。由于实际系统中发电机组众多，本文选择对系统稳定性影响较大的27个机组(G1～G27)作为研究对象[28]。

图8 某实际电网Fig.8 Actual power grid

用DSP-BPA进行电力系统仿真计算来获得相应数据。共获得800个样本，随机选取样本的3/4作为训练集，1/4作为测试集进行暂态稳定评估获得在线评价指标。

图9为不同τ值下Pin-SVM的评价指标情况对比。

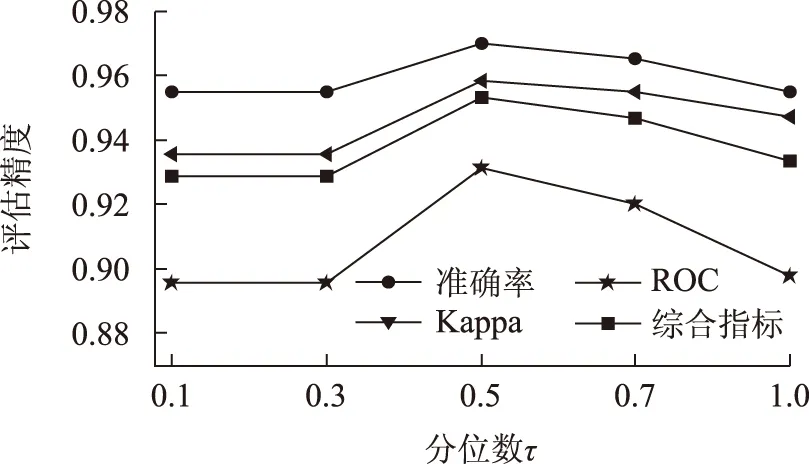
图9 某省实际系统不同τ值的评价指标Fig.9 Actual power grid evaluation indexes of different τ values

由图9可见，当τ=0.5时，评估精度最高达到0.953 2，τ=0.1、0.3时综合评价指标为0.928 7，也具有较高的评估精度，满足实际工程需要。而且随着τ值的增加，评估精度保持0.93左右，变化幅度很小始终保持较高的评估精度。由此可见，本文所提方法具有较高的评估精度和稳定性。

5 结论

本文提出一种将投影能量函数与Pin-SVM相结合的电力系统暂态稳定评估方法，并通过IEEE-39、IEEE-145及实际电网算例对所提方法的准确性和有效性进行验证，相关结论如下：

1)投影能量函数和系统整体状态密切相关，采用能量函数指标和系统指标构造原始特征集，可以降低特征集维数和减少冗余信息，是样本集构造的新思路。

2)采用最大相关最小冗余(mRMR)特征提取方法进行特征选择，可在原始样本集的基础上进一步减少冗余信息，降低特征维数，并搜索最优特征子集。

3)Pin-SVM改变两类之间最近点的位置，降低C-SVM受边界干扰样本的影响。在训练样本相同的情况下，该方法比C-SVM、nu-SVM和LSSVM具有更高的评估精度，同时指出径向基核函数为最佳核函数类型。

4)通过合理选择分位数τ确定边界函数，在确定边界函数时不依靠少数支持向量，受边界干扰样本的影响小，具有更强的稳定性。

[1] 姜涛，贾宏杰，姜懿郎，等.跨区互联电网热稳定安全域边界近似方法[J].电工技术学报，2016，31(8)：134-146. Jiang Tao，Jia Hongjie，Jiang Yilang，et al.Approximating method of wide area thermal security region boundary in bulk power system[J].Transactions of China Electrotechnical Society，2016，31(8)：134-146.

[2] 王亚俊，王波，唐飞，等.基于响应轨迹和核心向量机的电力系统在线暂态稳定评估[J].中国电机工程学报，2014，34(19)：3178-3186. Wang Yajun，Wang Bo，Tang Fei，et al.Power system on-line transient stability assessment based on response trajectory and core vector machine[J].Proceedings of the CSEE，2014，34(19)：3178-3186.

[3] 印永华，郭剑波，赵建军.美加“8.14”大停电事故初步分析以及应吸取的教训[J].电网技术，2003，27(10)：8-11. Yin Yonghua，Guo Jianbo，Zhao Jianjun.Preliminary analysis of large scale blackout in interconnected North America power grid on August 14 and lessons to be drawn[J].Power System Technology，2003，27(10)：8-11.

[4] 李春艳，孙元章，陈向宜，等.西欧“114”大停电事故的初步分析及防止我国大面积停电事故的措施[J].电网技术，2006，30(24)：16-21. Li Chunyan，Sun Yuanzhang，Chen Xiangyi，et al.Preliminary analysis of large scale blackout in Western Europe power grid on November 4 and measures to prevent large scale blackout in China[J].Power System Technology，2006，30(24)：16-21.

[5] 庄慧敏，巨辉，肖建.高渗透率逆变型分布式发电对电力系统暂态稳定和电压稳定的影响[J].电力系统保护与控制，2014，42(17)：84-89. Zhuang Huimin，Ju Hui，Xiao Jian.Impacts of inverter interfaced distributed generations with high penetration level on power system transient and voltage stability[J].Power System Protection and Control，2014，42(17)：84-89.

[6] 叶瑞丽，刘瑞叶，刘建楠，等.直驱风电机组风电场接入后的电力系统暂态稳定计算[J].电工技术学报，2014，29(6)：211-219. Ye Ruili，Liu Ruiye，Liu Jiannan，et al.Transient stability calculation of power system integrated with direct-drive wind farm with permanent magnet synchronous generators[J].Transactions of China Electrotechnical Society，2014，29(6)：211-219.

[7] 钱虹，黄正润，阮大兵.基于暂态零序电流变化率的小电流接地系统单相接地故障选线方法的研究[J].电气技术，2013，14(2)：27-30. Qian Hong，Huang Zhengrun，Ruan Dabing.The study of fault line selection′s method based on the change rate of transient zero sequence current for small current grounding system[J].Electric Technology，2013，14(2)：27-30.

[8] 王佳丽，刘涤尘，廖清芬，等.基于暂态能量的电力系统切机控制措施[J].电力系统保护与控制，2016，44(10)：1-9. Wang Jiali，Liu Dichen，Liao Qingfen，et al.Generator tripping strategy based on transient energy of power system[J].Power System Protection and Control，2016，44(10)：1-9.

[9] 张怡，吴文传，张伯明，等.暂态稳定预警与预防控制系统的开发和应用[J].电力系统自动化，2010，34(3)：44-48. Zhang Yi，Wu Wenchuan，Zhang Boming，et al.Development and application of early warning and preventive control system for transient stability[J].Automation of Electric Power Systems，2010，34(3)：44-48.

[10]顾雪平，李扬，吴献吉.基于局部学习机和细菌群体趋药性算法的电力系统暂态稳定评估[J].电工技术学报，2013，28(10)：271-279. Gu Xueping，Li Yang，Wu Xianji.Transient stability assessment of power systems based on local learning machine and bacterial colony chemotaxis algorithm[J].Transactions of China Electrotechnical Society，2013，28(10)：271-279.

[11]李扬，李国庆，顾雪平，等.基于集成OS-ELM的暂态稳定评估方法[J].电工技术学报，2015，30(14)：412-418. Li Yang，Li Guoqing，Gu Xueping，et al.Transient stability assessment of power systems based on ensemble OS-ELM[J].Transactions of China Electrotechnical Society，2015，30(14)：412-418.

[12]姚德全，贾宏杰，赵帅.基于复合神经网络的电力系统暂态稳定评估和裕度预测[J].电力系统自动化，2013，37(20)：41-46. Yao Dequan，Jia Hongjie，Zhao Shuai.Power system transient stability assessment and stability margin prediction based on compound neural network[J].Automation of Electric Power Systems，2013，37(20)：41-46.

[13]刘艳，顾雪平，李军.用于暂态稳定评估的人工神经网络输入特征离散化方法[J].中国电机工程学报，2005，25(15)：56-61. Liu Yan，Gu Xueping，Li Jun.Discretization in artificial neural networks used for transient stability assessment[J].Proceedings of the CSEE，2005，25(15)：56-61.

[14]邵雅宁，唐飞，刘涤尘，等.一种适用于WAMS量测数据的系统暂态功角稳定评估方法[J].电力系统保护与控制，2015，43(6)：33-39. Shao Yaning，Tang Fei，Liu Dichen，et al.An approach of transient angle stability assessment in power system for WAMS measured data[J].Power System Protection and Control，2015，43(6)：33-39.

[15]王康，孙宏斌，张伯明，等.基于二维组合属性决策树的暂态稳定评估[J].中国电机工程学报，2009，29(增刊)：17-24. Wang Kang，Sun Hongbin，Zhang Boming，et al.Transient stability assessment based on 2D combined attribute decision tree[J].Proceedings of the CSEE，2009，29(S)：17-24.

[16]孙宏斌，王康，张伯明，等.采用线性决策树的暂态稳定规则提取[J].中国电机工程学报，2011，31(34)：61-67. Sun Hongbin，Wang Kang，Zhang Boming，et al.Rule extraction in transient stability study using linear decision trees[J].Proceedings of the CSEE，2011，31(34)：61-67.

[17]李扬，顾雪平.基于改进最大相关最小冗余判据的暂态稳定评估特征选择[J].中国电机工程学报，2013，33(34)：179-186. Li Yang，Gu Xueping.Feature selection for transient stability assessment based on improved maximal relevance and minimal redundancy criterion[J].Proceedings of the CSEE，2013，33(34)：179-186.

[18]叶圣永，王晓茹，刘志刚，等.基于受扰严重机组特征及机器学习方法的电力系统暂态稳定评估[J].中国电机工程学报，2011，31(1)：46-51. Ye Shengyong，Wang Xiaoru，Liu Zhigang，et al.Power system transient stability assessment based on severely disturbed generator attributes and machine learning method[J].Proceedings of the CSEE，2011，31(1)：46-51.

[19]Huang X，Lei S，Suykens J A K.Support vector machine classifier with pinball loss[J].IEEE Transactions on Pattern Analysis & Machine Intelligence，2014，36(5)：984-997.

[20]Jumutc V，Huang X，Suykens J A K.Fixed-size Pegasos for hinge and pinball loss SVM[C]//Proceedings of the International Joint Conference on Neural Networks Pages，2013：1122-1128.

[21]Padiyar K R，Krishna S.Online detection of loss of synchronism using energy function criterion[J].IEEE Transactions on Power Delivery，2006，21(1)：46-55.

[22]房大中，宋文南，张尧.构造电力系统暂态能量函数新方法研究[J].中国科学，E辑，2003，33(11)：1007-1012. Fang Dazhong，Song Wennan，Zhang Yao.New method to construct transient energy function of power system[J].Science in China(Series E)，2003，33(11)：1007-1012.

[23]Fang Dazhong，Yang Jingang，Sun Wen，et al.Transient stability assessment using projection formulations[J].IET Generation，Transmission and Distribution，2009，3(6)：596-603.

[24]孙闻，房大中，薛振宇.电力系统在线暂态稳定分析方法[J].电网技术，2009，33(14)：16-20. Sun Wen，Fang Dazhong，Xue Zhenyu.A method for on-line analysis of power system transient stability[J]，Power System Technology，2009，33(14)：16-20.

[25]唐飞，王波，査晓明，等.基于双阶段并行隐马尔科夫模型的电力系统暂态稳定评估[J].中国电机工程学报，2013，33(10)：90-97. Tang Fei，Wang Bo，Zha Xiaoming，et al.Power system transient stability assessment based on two-stage parallel hidden Markov model[J].Proceedings of the CSEE，2013，33(10)：90-97.

[26]Farmer R G.Transient stability test systems for direct stability methods[J].IEEE Transactions on Power Systems，1992，7(1)：37-43.

[27]戴远航，陈磊，张玮灵，等.基于多支持向量机综合的电力系统暂态稳定评估[J].中国电机工程学报，2016，36(5)：1173-1180. Dai Yuanhang，Chen Lei，Zhang Weiling，et al.Power system transient stability assessment based on multi-support vector machines[J].Proceedings of the CSEE，2016，36(5)：1173-1180.

[28]姜涛，黄河，贾宏杰，等.基于投影寻踪最佳方向的同调机群识别方法[J].中国电机工程学报，2015，35(2)：359-367. Jiang Tao，Huang He，Jia Hongjie，et al.Coherency identification through projection pursuit[J].Proceedings of the CSEE，2015，35(2)：359-367.

(编辑 赫蕾)

Transient Stability Assessment in Bulk Power Grid Using Projection Energy Function and Support Vector Machine with Pinball Loss

ChenHouheWangChangjiangJiangTaoLiXueLiGuoqing

(School of Electrical Engineering Northeast Electric Power University Jilin 132012 China)

This paper proposes a novel transient stability assessment (TSA) method using support vector machine with pinball loss (Pin-SVM). A group of system-level and projection energy function classification features are first extracted from the power system operation parameters to build the original feature set of the transient stability index, such as average mechanical power, initial rotor acceleration, system shock, projection speed, projection acceleration and projection kinetic energy (PKE) and so on. Furthermore, a feature selection approach based on maximal relevance and minimal redundancy (mRMR) criterion is employed to evaluate the feature subset which has high sensitivity to transient changes. Then, feature sets are mapped to a higher dimensional space and the TSA problem is then transformed into a linear classification problem and use the quantile to change the closest point position between system stability class and unstable class, converts transient stability classification to the problem of finding the optimal quantile distance in Pin-SVM, which can reduce the influence of boundary interference samples. Finally, the simulated results of classic IEEE 39-bus system, IEEE 145-bus system and practical power grid demonstrate the feasibility and the validity of this proposed method.

Projection energy function，support vector machine with pinball loss(Pin-SVM)，wide area measurement system，transient stability assessment

国家重点研发计划(2016YFB0900903)、国家自然科学基金(51477027，51677022，51607033，51607034)和东北电力大学博士科研启动基金(BSJXM-201501)资助项目。

2016-05-22 改稿日期2016-08-04

TM712

陈厚合 男，1978年生，博士，教授，研究方向为电力系统安全性和稳定性。

E-mail：chenhouhe @126.com

姜 涛 男，1983年生，博士，副教授，研究方向为电力系统安全性和稳定性、可再生能源集成、综合能源系统。

E-mail：electricpowersys@163.com(通信作者)