环状多源配电网中考虑扰动源定位的PQM优化配置

翁国庆 黄飞腾 南余荣 谢志云 朱双双

(浙江工业大学信息工程学院 杭州 310023)



环状多源配电网中考虑扰动源定位的PQM优化配置

翁国庆 黄飞腾 南余荣 谢志云 朱双双

(浙江工业大学信息工程学院 杭州 310023)

兼顾网络化电能质量监测系统(NPQMS)构建成本和电能质量扰动源(PQDS)定位需求，提出了一种适用于环状多源配电网络的电能质量监测器(PQM)优化配置方法。通过分析环状多源配电网络拓扑结构特点，定义了系统结构信息描述矩阵、PQM配置一般性准则以及对应于不同属性端点的权重因子，建立PQM优化配置模型，并通过监测可观矩阵检验系统模糊度，筛选出最优的PQM配置方案。与通用PQDS定位方法中拓扑结构正方向的匹配性定义，保证了基于PQM优化配置结果实现PQDS精确定位的可行性，且可为采用阶段式NPQMS构建方案提供PQM最优配置决策依据。以IEEE-14节点环状多源配电系统为例，验证了所提PQM优化配置方法的可行性和有效性。

环状多源配电系统 电能质量监测器 优化配置 电能质量扰动源 模糊度

0 引言

未来智能配电网中，为有效监测和分析电能质量，向电网和用户提供实时可靠的质量指标、事故分析数据与诊断信息，构建能够实现多点连续在线测量以及信息融合的网络化电能质量监测系统(Networked Power Quality Monitoring System，NPQMS)已成为发展趋势[1，2]。然而，由于资金和技术的限制以及大范围配置电能质量监测器(Power Quality Monitors，PQM)带来的数据冗余和通信任务繁重等问题，如何实现NPQMS中PQM的优化配置具有重要意义[3]。

随着现代电网规模的增大，基于电力专家的实践认知来手动完成PQM的优化配置已变得不现实。根据专家经验总结出一般性准则，然后基于智能算法取代人工布点成为必然。文献[4]提出图论分析法，通过检验系统模糊度(SAA)是否满足全网可观测为判断依据来获取合适的PQM配置方案。但其过于依赖系统拓扑结构，未考虑各节点电能质量水平，对某些特殊负荷的监测存在误差。文献[5-10]提出的节点电能质量分析法及其各种改进法，以监测点数最少为目标、全网可观性为约束，建立PQM最优配置模型；然而因为数据的强随机特性，对非线性方程的线性化处理过程很可能出现不准确的情况，同时阈值设定困难。针对实际NPQMS往往采用分阶段安装导致系统并非完全可观测的情况。文献[11]提出一种不完全可观分析法，基于系统的冗余性指标建立两个阶段的优化模型，实现NPQMS未构建完成时使现有设备监测效果最大化，构建完成时系统配置最优化的优化目标。

PQM优化配置的研究虽已取得一些成果，但普遍仅适用于单电源辐射状配电网络，很少考虑环状、多源拓扑结构配网的适用性，以及与后继扰动源定位等智能诊断功能的匹配性。实际上，为提高供电的安全可靠性，配电网络普遍采用环形接线形式[12]。另一方面，未来能源互联网中分布式能源高渗透率接入，配电网拓扑结构将普遍变得多源复杂[13]。同时，未来NPQMS不仅满足于电能质量监测指标的可观性，必将更多地要求实现电能质量扰动源(Power Quality Disturbance Source, PQDS)定位等高级智能诊断功能[14-17]。

本文兼顾NPQMS构建成本和PQDS定位需求，提出一种适用于环状多源配电网络的PQM优化配置方法。首先，通过分析环状多源网络拓扑结构特点，构建系统结构矩阵和潮流方向矩阵以表征系统结构信息；其次，归纳出适用于环状多源网络的PQM配置一般性准则，定义权重因子量化表征各类属性端点的重要性程度；然后，以系统总权重最小化为目标建立系统PQM优化配置模型，并通过监测可观矩阵检验系统模糊度，筛选出最优的监测点配置方案。最后，基于IEEE-14节点系统对所提方法进行了有效性测试。

1 环状多源网络的结构信息描述

1.1 系统结构矩阵构建

图1为一个简单环状多源电网的拓扑结构，包含2个等效源、6条母线、7条连接线路和3个负载。根据环网结构的特点，因系统运行方式和状态的改变，每条线路的电流流向均存在多种可能，从而可能影响各节点配置PQM的监测范围。这要求进行目标系统PQM优化配置时，需考虑各种可能情况。

图1 正方向、双向等效线路和端点的定义Fig.1 Definition of positive direction，bidirectional equivalent circuit and endpoint

基于此，提出不同于常规电网结构分析时的几个定义：①正方向的规定：为匹配进行PQDS方向判定，需要建立一个固定坐标系——设定由母线指向线路方向为正方向，如图1箭头指向所示；②双向等效线路：将除电源、负载引出线外的每条线路均等效成两条并行双向的具有固定电流流向的线路，如图1虚线所示；③端点：将线路电流流入端设置为可配置PQM的端点，表示该线路，即每条线路可等效成两个端点进行表示。如图1中，端点编号对(t16，t61)分别表示母线1和母线6之间连线的双向等效线路。

邻接矩阵是一种常用于电力网络拓扑分析的追踪方法，其表达形式为Aorg=[ti1i2]NB×NB。其中，i1、i2=1,2,…,NB为母线节点编号，NB为系统母线节点数量，其矩阵元素为

(1)

(2)

据此，可得图1 所示系统的修正邻接矩阵为

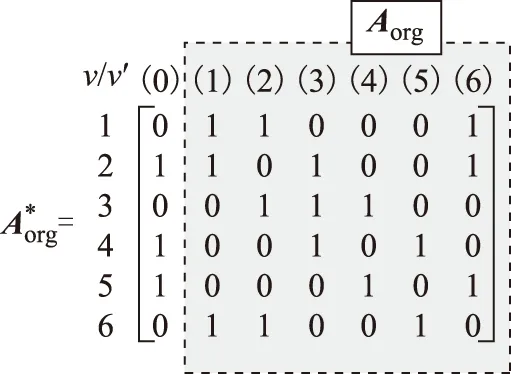
(3)

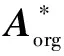
(4)

图1示例网络的系统结构矩阵如附录中式(A1)所示，其不受环网运行方式和状态的影响。

1.2 潮流方向矩阵构建

尽管环状多源系统运行方式和状态存在多种可能，但其绝大多数时间处于正常运行状态。因此，在PQM配置时，需优先保证系统正常运行状态下的全网可观。图2是图1示例系统在正常运行状态下的拓扑结构，虚线表示该状态下的系统电流方向。

图2 正常运行状态下的电网拓扑结构及单距区块划分Fig.2 Topology and division of single-distance section in normal running condition of the example network

通过比较电流方向和设定正方向，可对SSM矩阵进行修正，得到包含系统潮流信息的潮流方向矩阵CDM，如附录中式(A2)所示。CDM矩阵元素cji的赋值原则为

(5)

考虑系统拓扑结构中线路密集度对监测点配置的影响，基于系统正常运行状态下反映潮流方向的拓扑结构，对系统线路进行等效间距处理。如图2所示，选取拓扑结构图中相邻母线间最短的线路作为单元距离的标尺，各母线间线路的等效间距为整数倍单元距离，并以单元间距划分区块，命名为“单距区块”。单距区块内单元线路数量指不包含电源和负荷引出线的线路数量。

1.3 监测可观矩阵构建

若PQM被安装于网络某节点或线段中，根据各种电能质量扰动方向判定算法[18-20]，当系统发生电能质量扰动事件时，可以有效判定出PQDS与PQM的相对位置。扰动源的相对位置分为上游区域和下游区域，可根据电流方向来定义：电流从监测点流出的网络区域为下游区域；上游区域是指不包括在下游区域里的其他区域。图3显示了6节点示例系统中M1监测器的上游、下游区域划分。

图3 M1监测器的上、下游区域划分Fig.3 Upstream region and downstream region of M1

一旦目标电网完成监测器配置，根据正常运行状态下的潮流拓扑结构，可构建一个T×M的监测可观矩阵MCM，用以描述各PQM与各线路间的位置关系，可表征各监测器的可观范围。其中，M是系统中监测器的总数量，其元素mjr赋值原则为

(6)

式中，r为PQM的编号，r=1,2,…,M。

在图3示例系统中任意配置3个监测器(这里选择M1、M2、M3)以显示MCM矩阵元素，其对应监测可观矩阵如附录中式(A3)所示。例如，M1安装于线路端点t11处，对应的矩阵元素m11=1；其他沿着M1潮流方向上的所有端点对应的矩阵元素(即m21，m31，m41，m51，m71，m14,1m16,1m17,1m18,1m19,1)也均置值为1。

2 权重因子和模糊度指标

2.1 权重因子定义

2.1.1 监测器优化配置原则

由于现有主要针对辐射状配电网的经典PQM配置准则[4]在环状多源系统中并不能完全适用，本文根据后者结构特点并结合考虑PQDS定位需求，重新归纳出6条PQM布置的一般性准则：

1)准则1：N-1准则。根据基尔霍夫定律，只要与母线连接的任意N-1个端点上安装监测器，另一个端点的电能质量信息也可以获得。

2)准则2：负载支路上具有更高的权重。在选择N-1条安装监测器的线路时，用户负载被认为是重要的监测点，负载线路需优先考虑。

3)准则3：电源引出线具有最高的权重。电源作为供电端，根据监测器监测范围的特点，认为应该优先考虑电源引出线，作为重点监测对象。

4)准则4：同一条线路上优先只装一个。根据经济效益，不允许在同一条线路上安装多个监测器，即在选择N-1条线路时，优先考虑未安装过PQM的线路。

5)准则5：除负载引出线外与该母线相连的端点小于等于两个，此类端点权重较低；相应地，与该类端点属于同一线路的端点权重较高。

6)准则6：优先满足正常运行状态下全网可观。环网系统绝大多数时间处于正常运行状态，因此在配置监测点时需要优先保证此状态下系统拓扑结构的全网可观性。

2.1.2 权重因子的定义

基于上述准则可知，系统中不同端点具有不同性质，存在不同的重要程度。据此，可合理定义权重因子，实现“各个端点重要程度”的量化描述，使端点的性质在优化配置算法中得以体现。

为提高算法效率，首先对所有筛选出的有效端点进行运算编号和属性分类，如图4所示。

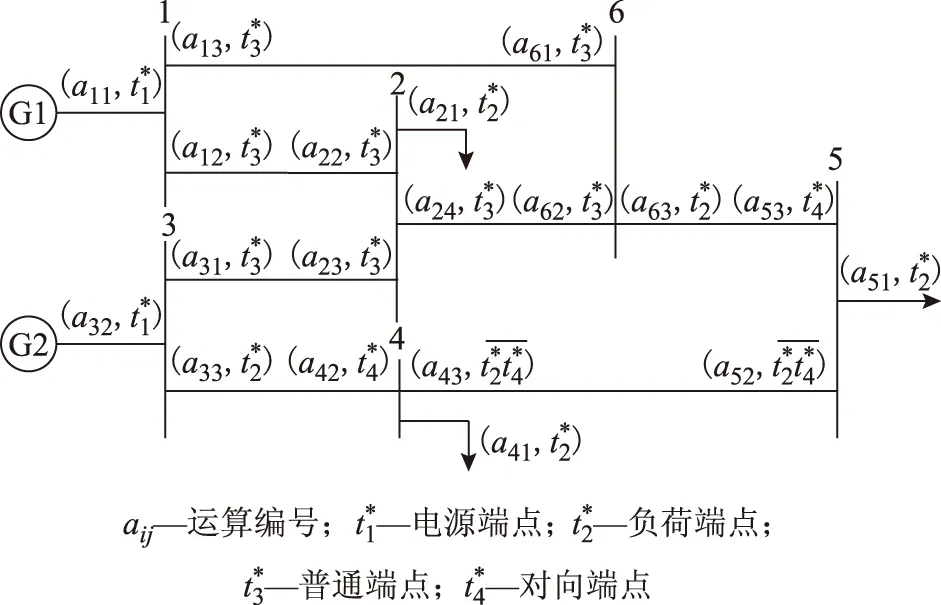
图4 等效网络的运算编号和属性分类Fig.4 Operation number and attributive classification of the equivalent network

结合这些属性和编号，定义αij、βij、γij三个权重系数来量化表征PQM布置的6条一般性准则：βij表征准则1；αij表征准则2、3、5；γij表征准则4、6。αij、γij、βij的数学表达式分别为

(7)

(8)

(9)

其中

(10)

(11)

(12)

(13)

将αij、γij、βij同时应用于PQM优化配置方程，可筛选出合适的方案。各权重系数的定义和取值说明：

1)αij是一个标准化值，表示与该母线i相连的几个端点中端点aij的重要程度；根据上述一般准则，对各类属性端点的权重值进行分配：ωt1/2=ωt2=2ωt3=4ωt4。

2)γij按各区块的密集程度和线路潮流方向的首末端分配权重，使得同一条线路上优先只装一个监测点，且其位置选取趋向于满足正常运行状态下的全网可观。

3)βij进一步降低了母线i上重要程度最低的端点权重值，表明这一端点可能到监测点数量足够充分时才会被选取，使其满足N-1配置准则。

2.2 模糊度指标定义

2.2.1 环状多源系统监测模糊指标定义

由于环状多源系统的电能流向非单一性，增加了电网电能质量准确监测和PQDS定位的难度，对PQM优化配置提出了更高的要求。因此，需更严格地规定PQM监测模糊的范畴：①安装有监测器的端点不模糊；②与同一条母线相连接的Ni个端点，安装有监测器的端点数量大于或等于Ni-1，则该Ni个端点不模糊；③除去安装过监测器的端点后仍存在两个与母线相连的端点时，若与其相连的端点不模糊，则这两个端点也不模糊。

若系统中布置的监测器的数量不够，部分端点不能被有效监测到，在识别端点时将会出现拓扑模糊。可采用两种模糊度指数的形式描述[3]，分别为系统整体模糊度(IEA)和部分最大模糊度(IMA)。

(14)

(15)

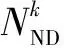
对IMA进行[0，1]归整处理，得到归一化的部分最大模糊度IMA′为

(16)

(17)

2.2.2 使用监测可观矩阵检查模糊度

监测系统的各模糊度指标可通过监测可观矩阵进行获取和校验，其主要流程为：①构建系统监测可观矩阵MCM；②对MCM矩阵进行分区域处理；③根据模糊规定1、2、3从各区域中排除各PQM；④计算各区域的bk；⑤计算IEA、IMA′、IA。

图5为6节点示例系统的拓扑模糊问题解决过程。为了检测模糊度，必须从监测可观矩阵找到每个区域，以及每个区域里端点的监测模糊程度。附录式(A4)是图5对应的监测可观矩阵，根据矩阵元素+1分类可得到各个区域：(t11，t16，t61)、(t12，t21)、(t20)、(t26，t56，t62，t65)、(t23，t32，t33)、(t34，t43，t45，t54)、(t40)、(t50)。在这些端点里，t11、t12、t20、t33、t34、t40是安装有监测器的端点；t16和t32遵循N-1准则，其不包含在模糊度指数计算中。当所有端点都检测完后，计算得到的模糊度指数为IEA=4/19，IMA′=0.088，IA=2.26。

基于扰动功率和扰动能量的经典PQDS方向判定法[18]的正方向定义与本文正方向定义具有高度匹配性。在正常状态下的潮流拓扑结构中，分析发生扰动时监测点上的扰动方向判定结果取值，与CDM矩阵比对相应元素的变化，即可判定PQDS与各PQM的相对位置。当监测点数量足够多，满足IA=0时，即可以将PQDS精确定位到具体线路上；当监测点数量不足以使IA=0时，将存在定位模糊(即只能定位到某一区域内)，且IA越小定位将越精确。

图5 示例系统拓扑模糊性Fig.5 Ambiguity of the topology in example network

3 优化方程的建立和求解

基于前述网络特性分析，以及特征矩阵、权重系数和模糊度指标的定义，可建立监测器最优布置的优化方程。

优化方程的目标函数和约束条件分别为

(18)

(19)

(20)

该优化方程本质上是一个线性规划问题，目标函数表明配置监测点后系统的总权重必须最小化。由于当且仅当端点tij不能被监测到时，对应的xij赋值为1，优化过程实际上是将非监测点的总权重进行最小化处理，即往往选取具有更高权重的端点作为监测点。约束条件表示监测点的数量受用户的经济能力和对系统的监测效益要求等综合因素约束，即由用户最终所能提供的监测点数量确定。

为得到最小的函数值，需设置更多的xij为0，优化过程将在约束允许的范畴内找到最优解。整个PQM优化配置算法流程如图6所示，其基本思路是：首先计算权重因子，基于其建立目标函数并在给定监测器数量下进行优化，确定监测器位置；然后，基于已知的监测器位置，构建监测可观矩阵，进而基于模糊度检测流程计算IA指数；经过多次迭代，最后确定监测器的最优数量和位置，使IA值在给定约束条件下最小化。

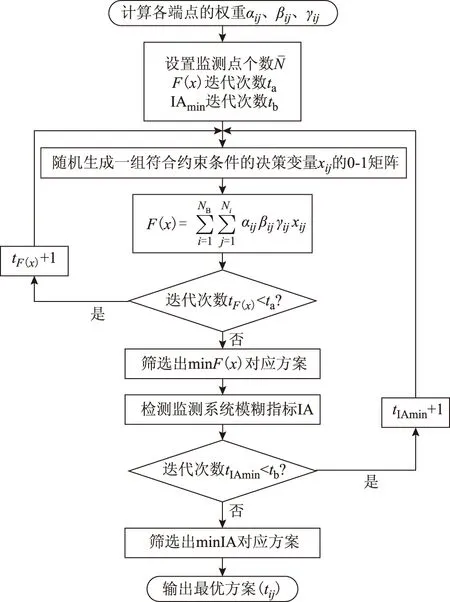
图6 监测点优化配置的算法流程Fig.6 Algorithm flow of optimum allocation of PQM

4 案例分析

以IEEE-14节点配电系统为例进行仿真分析[21]。该系统中共有5个电源、14条母线、11个负载，共计56个端点。首先，在Simulink中搭建系统仿真平台，分析系统在正常运行状态时各端点的电气量。基于潮流计算结果，可绘制系统拓扑结构，如图7所示。

图7 正常运行状态下IEEE-14节点系统潮流拓扑结构Fig.7 Flow topological of IEEE-14 node distribution system in normal running condition

根据系统仿真结果，以前述系统结构信息的描述方式和权重因子的定义为理论依据，可计算出系统中各端点权重因子αij、γij和βij的值。基于各端点的权重值，建立优化方程，然后进行优化求解，得到最优的监测点配置结果为{t11，t12，t22，t23，t24，t33，t34，t47，t52，t54，t60，t66，t6.12，t88，t94，t9.10，t9.14，t10.0，t11.0，t12.0，t13.0，t13.6}。此时，监测点数量为22个，系统监测模糊指标IA=0。根据监测点提供的方向判定信息和正常运行状态下的系统拓扑结构信息，可以实现将PQDS精确定位到具体线路上。

若系统所能提供的PQM数量少于22个，则系统将出现监测模糊。等间距地选取一组监测点数量，并分别根据这些给定数量进行PQM优化配置。经优化求解，筛选出各自最小IA时的优化配置方案，结果见表1。

表1 监测点数量不足时的IA及PQM最佳配置方案

图关系曲线Fig.

为更清晰地表征NPQMS中新增一个监测点对系统IA降低的贡献度，定义一个如式(21)所示新指标AREA(i)。式中S(i)的物理意义如图8中阴影三角面积所示，表征当系统中布置的PQM个数由i-1增加至i时，系统IA的降低速率(乘系数10的目的仅为使AREA(i)指标在图中合理显示)。

(21)

当监测点数量足够多，满足IA=0时，即可以将PQDS精确定位到具体线路上；当监测点数量不足以使IA=0时，系统将存在定位模糊(即只能定位到某一区域内)，且IA越小定位结果将越精确。若考虑采用阶段式NPQMS建设方案，PQM优化配置的目的是：当NPQMS建设完善时，可实现PQM配置最优化；而在NPQMS未建设完善时，使阶段式安装的监测装置使用效果达到最大化。

5 结论

为解决未来智能配电网中NPQMS构建成本及PQDS定位精确度两者间矛盾，能否有效实现PQM优化配置成为解决问题的关键。本文提出一种适用于环状多源网络并考虑PQDS定位需求的PQM优化配置算法。定义了正方向、双向等效线路和端点等新概念，并构建系统结构矩阵和潮流方向矩阵实现其结构信息表征。基于归纳的适用于环状多源网络的PQM配置一般准则，将定义的系统端点划分为电源端点、负荷端点、对向端点和普通端点4种不同属性，并分别定义权重因子量化表征其重要程度。定义了IEA、IMA和IA三种模糊度指数描述不同PQM配置方案进行端点识别时将会出现的拓扑模糊程度，并通过监测可观矩阵实现上述模糊度指数的获取和校验。以总权重最小化为目标建立了系统PQM优化配置模型，进行算法优化求解筛选出最优的PQM配置方案。最后，采用IEEE-14节点配电系统验证了所提PQM优化配置方法的可行性和有效性，且可为阶段式NPQMS建设方案提供PQM优化配置决策支持。今后，将进一步研究同时适用于辐射状和环状网络的普适性PQM优化配置方法。

附 录

(A1)

(A2)

(A3)

(A4)

[1]DemirciT，KalayciogluA，KucukDO，etal.Nationwidereal-timemonitoringsystemforelectricalquantitiesandpowerqualityoftheelectricitytransmissionsystem[J].IETGeneration，TransmissionDistribution，2011，5(5)：540-550.

[2] 陈雷，郑德忠，廖文喆.基于压缩感知的含扰动电能质量信号压缩重构方法[J].电工技术学报，2016，31(8)：163-171.ChenLei，ZhengDezhong，LiaoWenzhe.Methodbasedoncompressedsensingforcompressionandreconstructionofpowerqualitysignalswithdisturbances[J].TransactionsofChinaElectrotechnicalSociety，2016，31(8)：163-171.

[3] 翁国庆，张有兵.网络化电能质量监测与分析系统的设计[J].电力系统自动化，2008，32(15)：79-83.WengGuoqing，ZhangYoubing.Designofanetworkedpowerqualitymonitoringandanalysissystem[J].AutomationofElectricPowerSystems，2008，32(15)：79-83.

[4]WonDJ，MoonSI.Optimalnumberandlocationsofpowerqualitymonitorsconsideringsystemtopology[J].IEEETransactionsonPowerDelivery，2008，23(1)：288-295.

[5]IbrahimAA，MohamedA，ShareefH.Powerqualitymonitorplacementmethodusingadaptivequantum-inspiredbinarygravitationalsearchalgorithm[C]//IPEC2012ConferenceonPower&Energy，HoChiMinh，2012：404-413.

[6] 卫志农，吴霜，孙国强，等.多目标电能质量监测器的优化配置[J].电网技术，2012，36(1)：176-181.WeiZhinong，WuShuang，SunGuoqiang，etal.Optimalplacementofpowerqualitymonitorsbasedonmultiobjectiveevolutionaryalgorithm[J].PowerSystemTechnology，2012，36(1)：176-181.

[7] 陈礼频，肖先勇，张文海.考虑扰动源定位的电压暂降监测点最优配置[J].电力自动化设备，2014，34(2)：79-90.ChenLipin，XiaoXianyong，ZhangWenhai.Optimalallocationofvoltage-sagmonitorsconsideringdisturbance-sourcelocating[J].ElectricPowerAutomationEquipment，2014，34(2)：79-90.

[8] 周超，田立军.基于粒子群优化算法的电压暂降监测点优化配置[J].电工技术学报，2014，29(4)：181-187.ZhouChao，TianLijun.Anoptimumallocationmethodofvoltagesagmonitoringnodesbasedonparticleswarmoptimizationalgorithm[J].TransactionsofChinaElectrotechnicalSociety，2014，29(4)：181-187.

[9]AiWL，ShareefH，MohamedA，etal.Applicationofbinaryfireflyalgorithmforoptimalpowerqualitymonitorpositioning[C]//Proceedingsofthe2013IEEE7thInternationalPowerEngineeringandOptimizationConference，2013：386-390.

[10]徐岩，郅静.基于改进自适应遗传算法的PMU优化配置[J].电力系统保护与控制，2015，43(2)：55-62.XuYan，ZhiJing.OptimalPMUconfigurationbasedonimprovedadaptivegeneticalgorithm[J].PowerSystemProtectionandControl，2015，43(2)：55-62.

[11]杨春雨.计及N-1情况的电能质量监测装置阶段式优化配置[J].水电能源科学，2011，29(8)：196-198.YangChunyu.PhasingoptimalallocationofpowerqualitymonitoringdevicesconsideringN-1conditions[J].WaterResourcesandPower，2011，29(8)：196-198.

[12]李开文，袁荣湘，邓翔天，等. 含分布式电源的环网故障定位的改进矩阵算法[J].电力系统及其自动化学报，2014，26(12)：62-68.LiKaiwen，YuanRongxiang，DengXiangtian，etal.Improvedmatrixalgorithmforfaultlocationinringdistributionsystemwithdistributedgenerations[J].ProceedingsoftheCSU-EPSA，2014，26(12)：62-68.

[13]ChenPC，MalbasaV，DongY，etal.Sensitivityanalysisofvoltagesagbasedfaultlocationwithdistributedgeneration[J].IEEETransactionsonSmartGrid，2015，6(4)：2098-2106.

[14]唐轶，陈嘉，樊新梅，等.基于扰动有功电流方向的电压暂降源定位方法[J].电工技术学报，2015，30(23)：102-109.TangYi，ChenJia，FanXinmei，etal.Amethodfordetectingvoltagesagsourcesbasedondisturbanceactivecurrentdirection[J].TransactionsofChinaElectro-technicalSociety，2015，30(23)：102-109.

[15]黄擎，王志远.基于多点电流测量的输电线路故障定位方法的研究与分析[J].电气技术，2016，17(1)：104-107.HuangQing，WangZhiyuan.Researchandanalysisoffaultlocationmethodfortransmissionlinebasedonmultipointcurrentmeasurement[J].ElectricalEngineering，2016，17(1)：104-107.

[16]李妍，车勇，单强，等.智能变电站二次系统在线监测评估的研究[J].电力系统保护与控制2016，44(10)：66-70LiYan，CheYong，ShanQiang，etal.Researchonsecondarysystemon-linemonitoringandevaluationinsmartsubstation[J].PowerSystemProtectionandControl，2016，44(10)：66-70

[17]伊洋，刘育权，陈宇强，等.基于信息综合判断的智能变电站网络通信故障定位技术研究[J].电力系统保护与控制，2016，44(3)：135-140.YiYang，LiuYuquan，ChenYuqiang，etal.Researchofnetworkcommunicationfaultlocationtechniqueinsmartsubstationbasedoncomprehensiveinformationjudgment[J].PowerSystemProtectionandControl，2016，44(3)：135-140.

[18]ParsonsA，GradyW，PowersE，etal.Adirectionfinderforpowerqualitydisturbancesbasedupondisturbancepowerandenergy[J].IEEETransactionsonPowerDelivery，2000，15(3)：1081-1086.

[19]KongWei，DongXinzhou，ChenZhe.Voltagesagsourcelocationbasedoninstantaneousenergydetection[J].ElectricPowerSystemsResearch，2008，78(11)：1889-1898.

[20]ChangGW，ChaoJP，HuangHM，etal.Ontrackingthesourcelocationofvoltagesagsandutilityshuntcapacitorswitchingtransients[J].IEEETransactionsonPowerDelivery，2008，23(4)：2124-2131.

[21]舒立平，陈允平. 一种新的无功电力定价算法[J].电网技术，2004，28(5)：59-63，68.ShuLiping，ChenYunping.Anovelpricingalgorithmforreactivepower[J].PowerSystemTechnology，2004，28(5)：59-63，68.

(编辑 赫蕾)

Optimization Allocation of PQM in Meshed Multiple-Source Distribution Networks Considering PQDS Location

WengGuoqingHuangFeitengNanYurongXieZhiyunZhuShuangshuang

(College of Information Engineering Zhejiang University of Technology Hangzhou 310023 China)

In view of the construction cost of networked power quality monitoring system (NPQMS) and the location requirement of power quality disturbance source (PQDS), a method for optimal allocation of power quality monitors (PQM) in meshed multiple-source distribution networks is proposed. Through characteristics analysis of the topology of meshed multiple-source networks, the matrixes of structure information is described, general principles of PQM allocation and weighted factors corresponding to different endpoints are defined. With establishing of the optimal model of the optimum allocation for monitoring points, the optimum position monitoring arrangement can be obtained by inspecting the system ambiguity through monitoring observability matrix. The definition of positive direction in this method matches with that in the general methods for PQDS location, which makes the accurate location of the PQDS feasible which based on the results of the optimization allocation of PQM. It can also offer decision support to the stagewise construction scheme of the NPQMS. Finally, with the example of the IEEE 14-bus system, the feasibility and validity of the presosed method are demonstrated.

Meshed multiple-source distribution networks，power quality monitors，optimization allocation，power quality disturbance source，ambiguity

国家自然科学基金(51207139，51407160)和浙江省自然科学基金(LY17E070005)资助项目。

2016-05-29 改稿日期2016-09-07

TM711

翁国庆 男，1977年生，博士，副教授，硕士生导师，研究方向为智能电网、电能质量监测与控制等。

E-mail：wgq@zjut.edu.cn

南余荣 男，1966年生，博士，教授，博士生导师，研究方向为电力传动及其自动化、电力电子技术等。

E-mail：nyr@zjut.edu.cn(通信作者)