多区间多列车动态杂散电流建模分析

田 涌

(青岛市西海岸轨道交通有限公司,266555,青岛∥高级工程师)



多区间多列车动态杂散电流建模分析

田 涌

(青岛市西海岸轨道交通有限公司,266555,青岛∥高级工程师)

城市轨道交通普遍采用直流牵引供电系统,多变电所多列车并列运行,线路上所有变电所均有可能向各列车供电。针对多区间多列车杂散电流动态分布,建立了多电源叠加的杂散电流分布模型,仿真分析出全线杂散电流、钢轨电位、排流网对地电位等相关参数随时间、位置的变化。所提出的仿真模型及结果可有效应用于直流牵引供电系统回流参数动态规律分析。

城市轨道交通; 杂散电流; 钢轨电位; 动态模型

Author′s address Qingdao West Coast Railway Co.,Ltd.,266555,Qingdao,China

城市轨道交通普遍采用直流牵引供电方式,牵引电流由接触网流向列车,回流电流经走行轨返回牵引变电所负极,回流系统采用悬浮接地方式。由于走行轨自身具有一定的纵向电阻,回流电流流经走行轨会产生一定的压降,该压降分布在轨地之间,形成钢轨电位[1]。走行轨虽然采用绝缘安装,但实际线路中绝缘往往较差,会有一部分回流电流由轨道泄漏,流向周边,形成杂散电流[2]。杂散电流会对城市轨道交通自身结构钢筋及周边埋地金属管线产生电化学腐蚀,严重影响其运行安全[3- 4]。

针对城市轨道交通杂散电流分布规律分析及建模,现有模型一般仅进行静态分布分析[5],仿真某一时刻列车在某一固定位置下一个区间的杂散电流的分布,且一般假设列车牵引电流均由其所在供电区间两端的变电所提供。而直流牵引供电系统接触网全线贯通,线路上运行的所有变电所和列车并列运行[6],各变电所和各列车之间相互影响,杂散电流、钢轨电位的分布均受其影响。本文针对多区间多列车并列运行下全线杂散电流、钢轨电位等参数建立动态分析模型。模型基于全线列车、变电所供电潮流计算结果,可有效进行全线各位置相关参数随时间动态变化的仿真分析。由于现场测试中很难对同一时刻全线各位置参数进行同时测试,而同一位置不同时间变化下相应参数测试操作性强,因此本文提供的仿真方法可有效应用于现场杂散电流等相关参数规律分析。

1 模型建立

1.1 各变电所电流计算

为进行多区间多列车杂散电流动态分析,需要了解全线各变电所电流随列车牵引电流变化情况。列车牵引电流及位置在不同区间随时间的变化情况可由列车牵引计算获得[7]。在此基础上,需进行直流牵引网潮流计算,由此得到全线各变电所电流随列车牵引电流变化的情况。

本文在变电所牵引电流计算过程中,列车等效为理想电流源,变电所等效为理想电压源与等效电阻串联电路,则变电所牵引电流计算等值电路如图1所示。图1中:Rj表示接触网电阻,与列车至牵引变电所的距离有关;Req表示牵引变电所等效电阻,它受牵引供电系统交流电源系统阻抗、整流元件电压降、整流变压器阻抗以及整流电路工作状态等影响,但在实际计算中,可简单通过整流机组外特性曲线获取;S表示变电所理想电压源;J表示列车理想电流源。

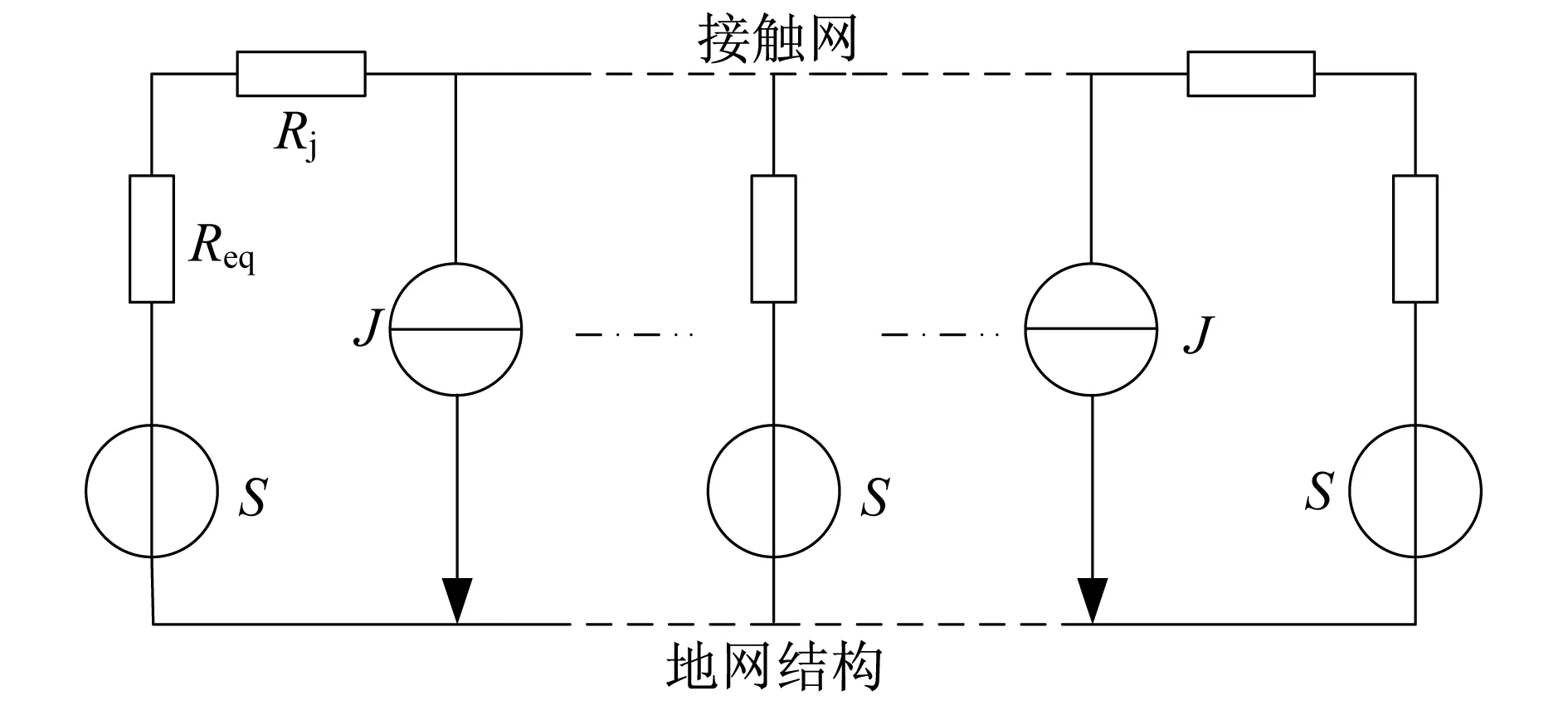
图1 变电所牵引电流计算等值电路

根据牵引电流计算等值电路,建立电路的节点电压方程,利用迭代法可求解各变电所电流随列车牵引电流的变化情况。

1.2 杂散电流模型构建

多电源叠加杂散电流分布模型构建过程中将全线列车以及牵引变电所均看作直流电源,共同对回流系统结构注入电流。先求出单电源模型下杂散电流、钢轨电位的分布情况,然后再将各电源分别作用的结果进行有效叠加计算,获取整条线路杂散电流、钢轨电位分布情况以及杂散电流的泄漏量。由于列车位置在供电区间内随运行工况而发生瞬时变化,每个单独电源向回流系统结构注入电流时,左右供电区间会按一定规则分配回流电流。

为简化理论分析过程,地铁杂散电流模型结构采用钢轨-排流网-大地3层电阻模型。同时,假定回流系统参数分布均匀,将4根钢轨等效为单根钢轨。

单电源模型等值电路如图2所示。

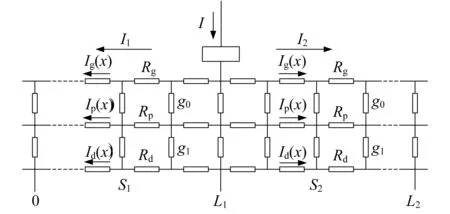
图2 单电源模型等值电路

图2中,I为单电源模型中注入回流系统的电流,I1为0～L1区段走行轨流经的电流,I2为L1～L2区段走行轨流经的电流;Rg为钢轨单位长度纵向电阻,Rp为排流网单位长度纵向电阻,Rd为大地单位长度纵向电阻;Ig(x)为钢轨x处电流,Ip(x)为排流网x处电流,Id(x)为大地x处电流;g0为钢轨与排流网之间过渡电导,g1为排流网与大地之间过渡电导；L1为列车距离左边变电所距离,L2为列车距离右边变电所距离。单电源模型是基于单列车双边供电模型得出的,可以看作是电源在整个牵引供电区间的大双边供电。以列车位置为边界点将供电区间分为左右两部分。其中:0～L1为左供电区间,L1～L2为右供电区间。通过理论分析可知,两边牵引电流分配计算公式如下:

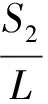
(1)

式中:

S1——0～L1供电区间长度;

S2——L1～L2供电区间长度;

L——供电区间总长度。

根据基尔霍夫电压、电流定律,单电源模型下左供电区间的钢轨电流、钢轨电位数学表达式为:

(2)

式中：

U11(x)、U21(x)、Ig1(x)、Ip1(x)——分别为0～L1供电区间内x位置钢轨电位、排流网电位、轨道电流、排流网电流；

f1，…，f4——非齐次微分方程组特解；

λ1，…，λ4——矩阵的特征值；

[b1ib2ib3ib4i]T——特征值λi对应的特征向量；

C1，…，C4——由初始条件决定的常数系数。

则左供电区间杂散电流为:

Is1=I1-Ig1

(3)

根据边界条件的不同,可得如下右供电区间的钢轨电流、钢轨电位数学表达式为:

(4)

式中：

U12(x)、U22(x)、Ig2(x)、Ip2(x)——分别为L1～L2供电区间内x位置钢轨电位、排流网电位、轨道电流、排流网电流；

f5，…，f8——非齐次微分方程组特解；

λ5，…，λ8——矩阵的特征值；

[b1ib2ib3ib4i]T——分别为特征值λi对应的特征向量；

C5，…，C8——由初始条件决定的常数系数。

则右供电区间杂散电流为:

Is2=I2-Ig2

(5)

整理式(2)～(5),并根据单电源注入电流的大小以及注入位置等关系分析计算,可以获取单电源模型下,全线杂散电流、钢轨电位等的分布情况,以及杂散电流的具体泄漏量。

有些陕西美食文化具有深刻的寓意，往往是某一历史人物或者故事典故，而在这些美食翻译时没有考虑到美食背后的文化渊源，采用机械式翻译的方法，难以表达出美食本身所富含的文化。比如把“金线油塔”直接翻译成“Crispy Fride Noodles”。

多电源叠加模型是单电源模型的叠加。多电源即表示地铁线路上所有牵引变电所、列车的位置、电流大小。在模型构建过程中将变电所与列车均看作直流电源,共同对回流结构注入电流,原理如图3所示。

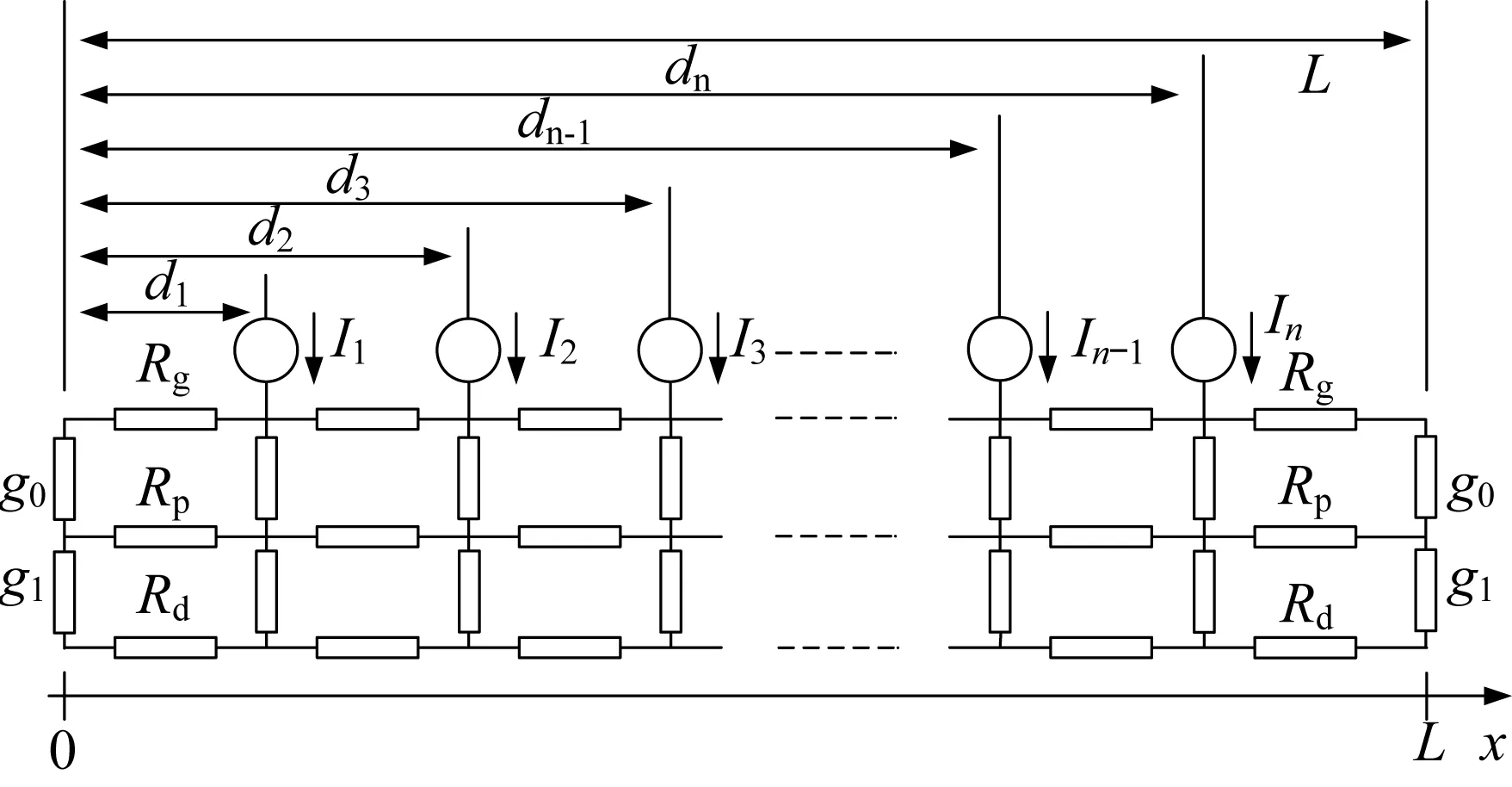
图3 多电源叠加模型原理图

图3中,I1～In表示区间n个注入电源的供电电流,d1～dn表示区间n个注入电源离起点的距离。假定地铁供电区间列车的始发位置为0点位置,线路上运行的列车与变电所共有n个,以各注入电源的位置为分界点,将整个地铁供电区间分成若干部分。根据单电源模型理论基础,首先求出单电源作用下某时刻、某位置的杂散电流、钢轨电位的大小;再根据叠加原理,将此时刻各电源分别在此位置作用的结果进行叠加计算,获取此时刻此位置的杂散电流及钢轨电位的大小,得到此时刻两注入电源间区段的杂散电流、钢轨电位分布情况;最后得到地铁整个供电区间杂散电流、钢轨电位的分布与杂散电流泄漏情况。

以注入源为分界点,各区间钢轨电位、钢轨电流、杂散电流等的计算公式如下:

0～d1区间段

d1～d2区间段

以此类推,dn～L区间段

运用叠加原理,通过以上表达式分析计算处理,可以求出多列车多牵引变电所运行工况下,地铁供电区间任意时刻、任意位置的钢轨电位、钢轨电流以及杂散电流的分布情况。由于多电源叠加模型在分析计算中,考虑到多列车、多变电所以及它们之间的相互影响,因此,通过模型得到的杂散电流、钢轨电位分布更符合地铁的实际情况。

2 仿真分析

2.1 仿真参数

基于上述模型,对线路杂散电流动态变化进行仿真。仿真参数设置如下:地铁全线区间长度为20.5 km,共有8座牵引变电所,其位置分别为0.50、2.35、5.62、8.13、12.07、15.24、17.93、20.00 km。钢轨纵向电阻Rg=0.03 Ω/km,排流网纵向电阻Rp=0.001 Ω/km,大地纵向电阻Rd=0.001 Ω/km,钢轨-排流网之间过渡电导率g0=(1/15) S/km,排流网-大地之间过渡电导率g1=(1/3) S/km。仿真时间长度为100 s,在此期间,全线有3列车在线路上运行,其牵引电流变化及位置变化如图4所示。

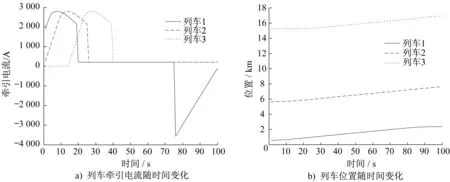
图4 列车牵引电流及位置随时间变化情况

2.2 不同时刻全线不同位置杂散电流动态变化

对该时间段进行仿真分析,得到全线不同位置钢轨电位、杂散电流、排流网对地电位随时间动态变化情况如图5所示。

图5 不同时刻全线不同位置参数动态变化仿真云图

由图5可知,由于全线各变电所均会向线路上运行的列车供电,回流系统杂散电流、钢轨电位等相关参数呈连续变化。由图5中动态分布图可有效判断全线钢轨电位、杂散电流等参数最大值所在的位置和所处的时刻。例如,钢轨电位最大值为86.8 V,所出现的位置位于15.45 km处,时间发生在27 s。

2.3 相同时刻全线不同位置杂散电流分布

进一步分析,可取不同时刻全线不同位置杂散电流等参数变化曲线进行分析。图6给出40 s时全线钢轨电位、杂散电流与排流网对地电位的分布情况。

图6可直观反映某一时刻,全线钢轨电位、杂散电流等参数出现的位置。例如,此时全线钢轨电位最大值为4.6 V,位于15.65 km处;全线杂散电流最大值为1.1 A,位于13.6 km处；全线排流网对地电位最大值为19.2 mV,位于6.3 km处。

2.4 同一位置不同时刻杂散电流变化

仿真结果同时可用同一位置不同时间下杂散电流等相关参数变化曲线描述,如图7所示。该图可直观反映出某一位置,各参数随时间的动态变化情况。

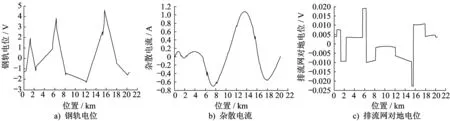
图6 同一时刻(40 s时)全线不同位置相关参数分布

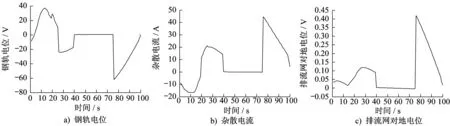
图7 同一位置(4.5 km处)不同时刻相关参数随时间变化

3 结语

本文针对多区间多列车动态运行下杂散电流相关参数动态变化,建立了基于潮流计算及多电源叠加的动态模型,仿真分析了全线多变电所多列车运行时各参数的变化情况。该建模方法可应用于实际线路杂散电流的动态规律分析。

[1] 王猛.直流牵引供电系统钢轨电位与杂散电流分析[J].城市轨道交通研究,2005(3):24-26.

[2] 李威.地铁杂散电流监测及防护技术[M].徐州:中国矿业大学出版社,2004.

[3] 杨向东,周晓军.外加直流电腐蚀钢筋引起混凝土破坏机理的研究[J].西部探矿工程,1999,11(4):92-96.

[4] 周晓军,高波,郭建国,等.混凝土中钢筋受外直流电腐蚀对其强度影响的试验研究[J].地铁与轻轨,2001(4):17-23.

[5] 庞原冰,李群湛.地铁杂散电流模型讨论[J].重庆工学院学报(自然科学版),2007(11):110-113.

[6] 刘炜.城市轨道交通列车运行过程优化及牵引供电系统动态仿真[D].成都：西南交通大学,2009.

[7] 尹航,蒋涛,张言伟,等.列车牵引计算分析及仿真[J].大连交通大学学报,2013,34(1):80-84.

Analysis of Dynamic Stray Current Modeling of Multi Train Running in Multi Intervals

TIAN Yong

DC traction power supply system is widely used in urban rail transit system, in which all the substations are possible to provide power for all trains in operation. According to the dynamic distribution of stray current in multi trains running in multi intervals, a dynamic simulation model of stray current with multi power composition is established. In which, changes of stray current,rail potential,drainage net potential and other related parameters with time and location are simulated.The model can be effectively applied to the dynamic analysis of reflux parameters.

urban rail transit; stray current; rail potential; dynamic model

U 223.6+2

10.16037/j.1007-869x.2017.05.013

2015-11-21)