基于机器学习在空气质量指数中的应用*

刘 锋, 李春燕, 谭祥勇, 王鹏飞

(1.重庆理工大学 数学与统计学院,重庆400054；2.上海财经大学 统计与管理学院, 上海 200433)

基于机器学习在空气质量指数中的应用*

刘 锋1, 李春燕1, 谭祥勇2, 王鹏飞1

(1.重庆理工大学 数学与统计学院,重庆400054；2.上海财经大学 统计与管理学院, 上海 200433)

利用机器学习和多元线性回归模型对西安市近一年的空气质量指数进行了研究, 首先利用随机森林思想对数据进行了补齐, 然后运用交叉验证对神经网络模型选取最优的隐层节点数和训练周期数，最后，通过比较两种模型的拟合效果发现，神经网络模型在对空气质量指数的预测效果明显好于多元线性回归模型。

神经网络;多元线性回归模型;空气质量指数

目前，随着人类科学技术的迅猛发展，大气污染状况日益加剧，空气质量成了人们密切关注的一个热门话题。空气质量监测局采用空气质量指数(Air Quality Index,AQI)对空气质量进行度量，数值是定量描述空气质量的无量纲指数，数值越大说明空气污染状况越严重。空气质量指数的分项监测指标为SO2，NO2、可吸入颗粒物、细粒颗粒物PM2.5、O3和CO，其中的罪魁祸首就是PM2.5,此物质粒径小，面积大，活性强，易附带有毒、有害物质，且在大气中的停留时间长、输送距离远,对人体健康有非常严重的影响。有研究认为，AQI监测指标中的SO2，NO2、CO等是在一定环境条件下形成的PM2.5的主要气态物体。因此，通过其他几个指标来对PM2.5指标进行预测是可行的。出于对人们健康的考虑，对PM2.5指标的预测具有相当重要的意义。

关于空气质量指数方面已有很多学者[1-2]分别采用不同的模型对其进行了研究。现研究是基于神经网络模型中应用最为广泛的BP神经网络模型，以西安市2015-08-17—2016-08-16共364 d的日全市平均空气质量指数为研究对象。通过多元线性回归模型和BP神经网络模型分别对数据进行研究，最终对两模型的预测结果进行拟合，对比发现神经网络模型的预测效果明显优于多元线性回归模型。

1 预备知识

1.1 神经网络

在人工神经网络中，多层感知器是运用最为广泛的模型,关于神经网络的研究可见文献[3-5]。一个典型的神经网络模型由3部分组成：输入层、隐藏层和输出层。对于一个具有r个输入变量，t个隐节点，s个输出节点的单一隐藏层神经网络模型，αs和βs分别代表对应节点之间的权值，f和g分别表示隐节点和输出节点的激活函数。用X=(X1,X2,...,Xr)T表示输入节点向量，Y=(Y1,Y2,...,Yr)T表示输出节点向量，Z=(Z1,Z2,...,ZT)T表示隐节点向量。记Uj=β0j+XTβj，Vk=α0k+ZTαk。则，

Zj=fj(Uj),j=1,2,…,t

μk(X)=gk(Vk),k=1,2,…s

其中，βmj表示输入节点Xm与隐节点Zj之间的权值，β0j表示对于隐节点的偏差；αjk表示隐节点Zj与输出节点YK之间的权值，α0k表示对于输出节点的偏差。βj=(β1j,β2j,...,βrj)T，αk=(α1k,α2k,...,αtk)T。因此，第k个输出节点如下：

其中，

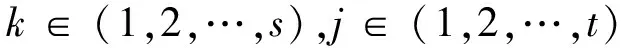
通常通过极小化误差平方和ESS来确定节点之间的最优权值：

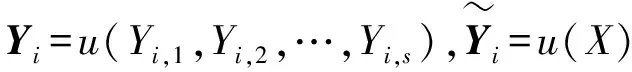
对于BP神经网络模型，模型的主要特点是：包含隐层，反向传播，激活函数采用(0,1)型Sigmoid函数。通过对神经网络模型进行训练，寻找出使该模型达到最好效果的隐层节点数和最优迭代次数。此过程是一个不断向样本学习的过程，因为每个样本都会提供关于输入输出变量数量关系的信息，因此需要依次向每个观测学习。如果所有观测学习结束后，模型给出的预测误差仍然较大，则需进行新一轮学习，直到满足学习终止条件为止。

1.2 随机森林

随机森林[6]是一种很新的机器学习模型，其具有自身独特之处并且能够达到很好的分类效果。在20世纪80年代，Breiman等人就发明了分类树算法。直到2001年，Breiman等把分类树组合成随机森林。其算法的实质是基于决策树的分类器算法。通过自助法(Boot-Strap)重采样技术[7]，从原始训练样本集N中有放回地重复随机抽取k个样本生成新的训练样本集，然后根据自助样本集生成k个决策树组成的随机森林，新数据的分类结果按决策投票多少形成的分数而定。其实就是对决策树算法的一个改进，将多个决策树合并在一起。单棵决策树的分类能力毕竟有限，在随机产生大量决策树后，分类能力会有很大的提高。这样就可以通过综合每一棵树的分类结果后对测试样本选择最可能的分类，因而达到较好的分类效果。

2 数据处理

研究对象是西安市2015-08-17—2016-08-16共364 d的日全市平均的空气质量指数，数据来源于http://www.xianemc.gov.cn/sxmpcp_qt.asp?ld=%D6%CA%C1%BF%C8%D5%B1%A8。

把数据分为测试集(2016-07-12至2016-08月16共有34组数据)和训练集(剩下的330组数据)两部分。运用训练集建立模型，测试集评判模型。表1列出了观测数据的连续某几天的指标值。

从表1中可以很明显地看出统计的数据中有缺失值的存在，这是数据中常会出现的问题，缺失数据的存在会对分析工作的进行造成很大影响。但数据的使用者和分析者往往缺乏处理缺失值方面的知识，仅仅对数据进行简单的删除或插补会影响数据规模和数据结构，进而影响分析结果。

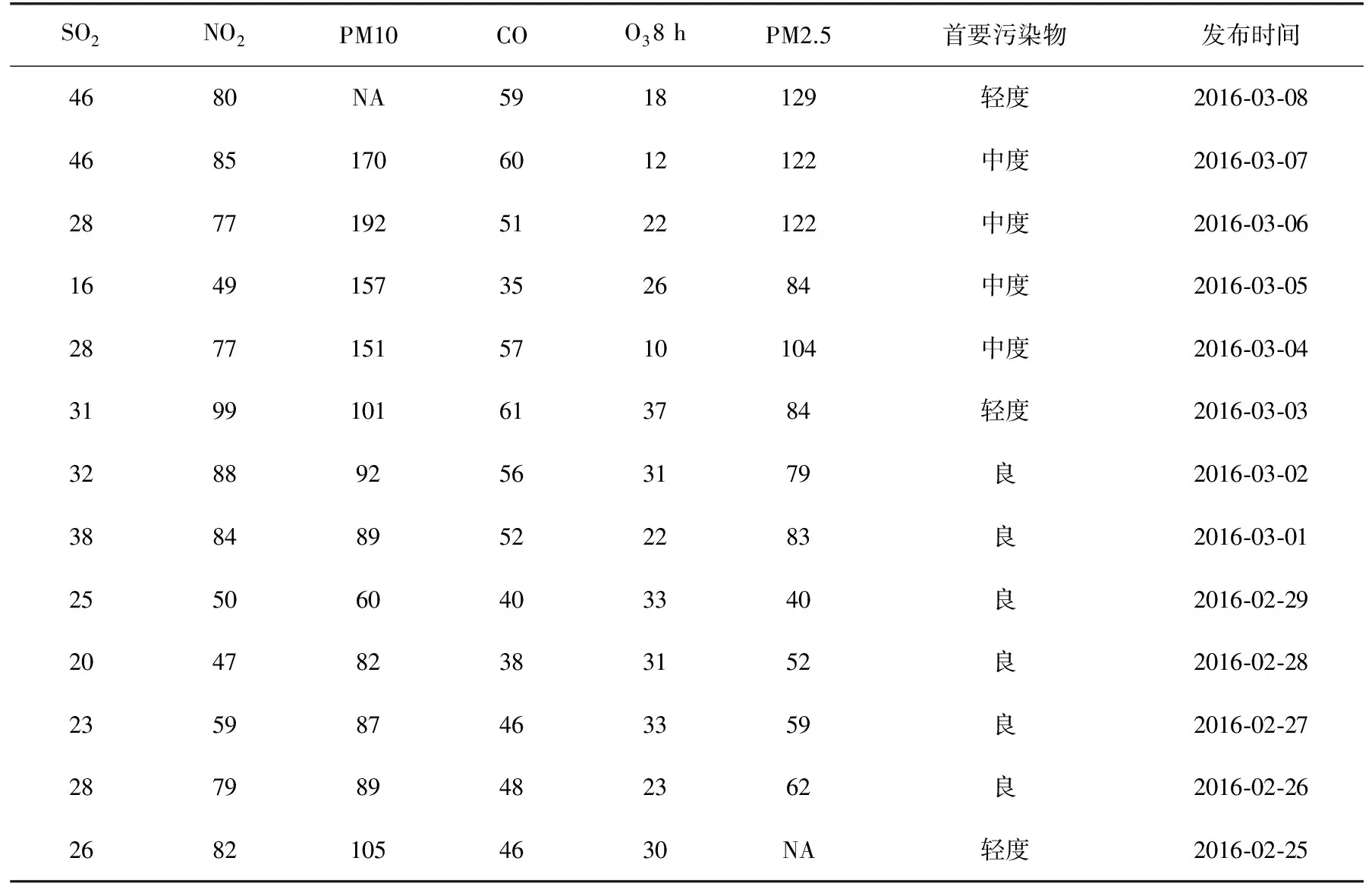
表1 西安市日平均空气质量指数

2.1 缺失值补全

要确保分析结果的可信度，必须对缺失值补全，常见的缺失值补全方法有个案剔除法、均值替换法、热卡填充法、回归替换法、多重替代法等。采用R语言中的MissForest函数对缺失值进行补齐，函数是通过随机森林的相关理论来实现的，它可以适用于离散、连续类型的数据，达到的效果很好，

2.2 数据归一化

在神经网络模型中，输入变量的取值范围通常要求为0～1，其目的是取消各维度数据间数量级的差别，避免输入变量的不同数量级直接影响权值的确定、加法器的计算结果以及最终的预测结果，造成网络预测误差较大。在对缺失值补全后，再对数据进行归一化处理，采用极差法对数据进行归一，即

其中，xmax和xmin分别为向量x的最大值和最小值。

3 研究过程

分别运用了多元线性回归和BP神经网络两个模型进行研究。

3.1 BP神经网络模型

研究是基于BP反向传播模型，模型为多层感知机结构，其中不仅包含输入和输出节点，而且还有一层或多层隐层。首先必须确定出该模型的结构，即隐藏层数和隐节点个数。然而，在对于隐藏层数这个问题上据实验表明：选择一个隐层的网络是最合适的。因此，只需要选取一个合适的隐节点数。采用10折交叉验证(10-fold cross validation)选取合适的隐节点数，在隐节点数确定的基础上再次使用10折交叉验证确定出训练周期。

3.1.1 交叉验证

用交叉验证的目的是为了得到一个可靠稳定的模型，目的是要使预测误差达到最小。运用10折交叉验证将数据集分成10份，轮流将其中9份做训练，1份做测试。最终通过NRESS值来选取出最优节点数和训练周期，通过选取使值达到最小或值不再变小的参数来作为最优节点数和训练周期。NRESS值表达式如下：

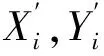
3.1.2 选取节点数与训练周期

一个合适的隐节点数与训练周期对于一个神经网络模型起着相当重要的作用，隐节点数与训练周期过多都可能会导致过拟合问题。在先确定出隐节点数的基础上再确定出训练周期。

由图1可知隐节点数为6个，由图2可知练周期确定为800。最终，确定了神经网络模型的结构，即含有一个隐藏层，隐藏层节点数为6个，训练周期为800。具体神经网络结构可见图3。

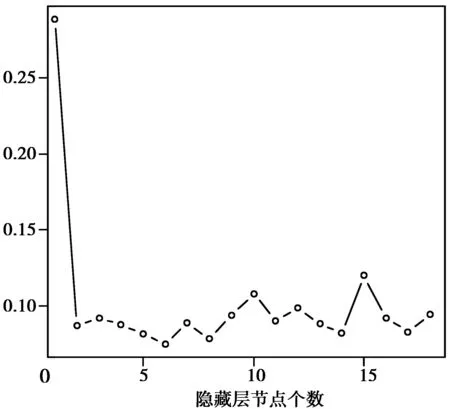
图1 隐藏层节点数Fig.1 Number of hidden layer nodes

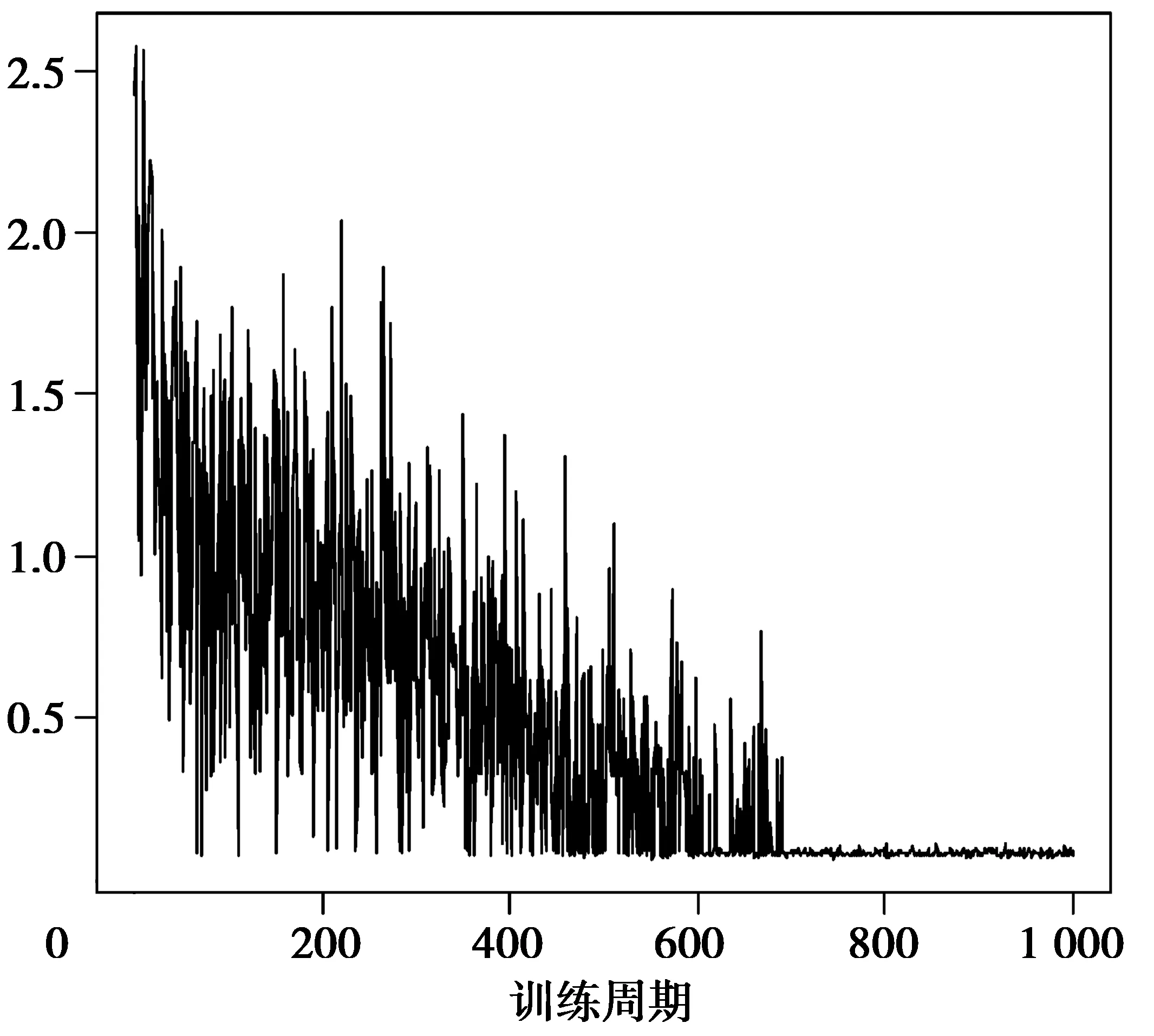
图2 训练周期Fig.2 Training period

图3 神经网络结构图Fig.3 Structure of neural network

3.2 多元线性回归模型

PM2.5为响应变量Y,自变量SO2，NO2、可吸入颗粒物、O3和CO分别对应为X1,X2,…,X5,通过R软件计算可得

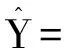
0.78X3+0.32X4+0.98X5

4 结果分析

最后对模型做测试时需把数据还原，在此基础上分别运用多元线性模型和神经网络模型对PM2.5的值进行预测。图4展示了神经网络模型预测值与真实值的拟合：在图4中可以清楚看出，神经网络模型的拟合效果能够很接近真实值。

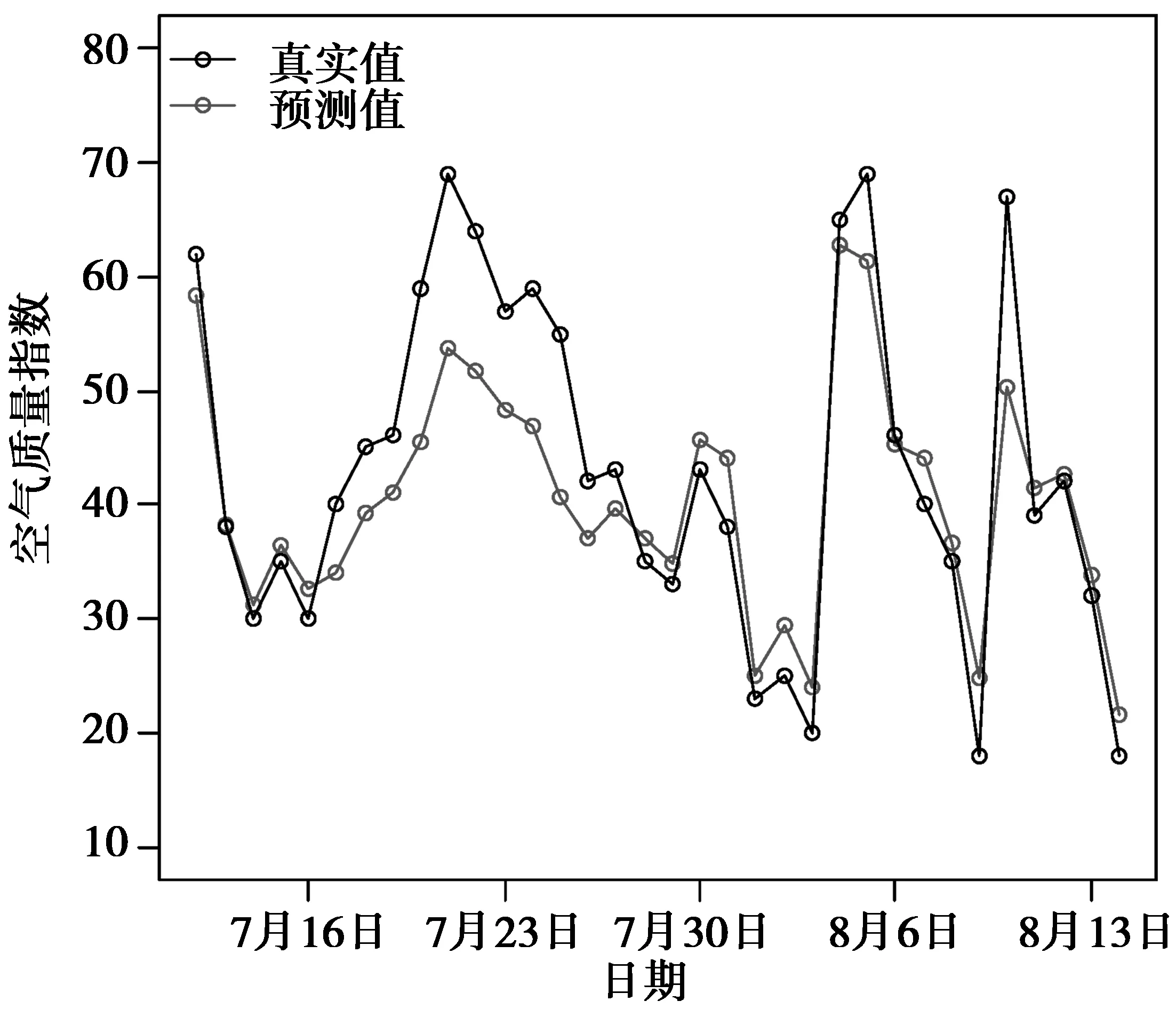
图4 神经网络预测值与真实值对比Fig.4 Comparison of the predictive value and the real value of the neural network

表2列出了2016-07-12—2016-08-14的32组PM2.5的真实值，分别运用神经网络模型和多元线性回归模型做出的预测与真实值之间的比较：

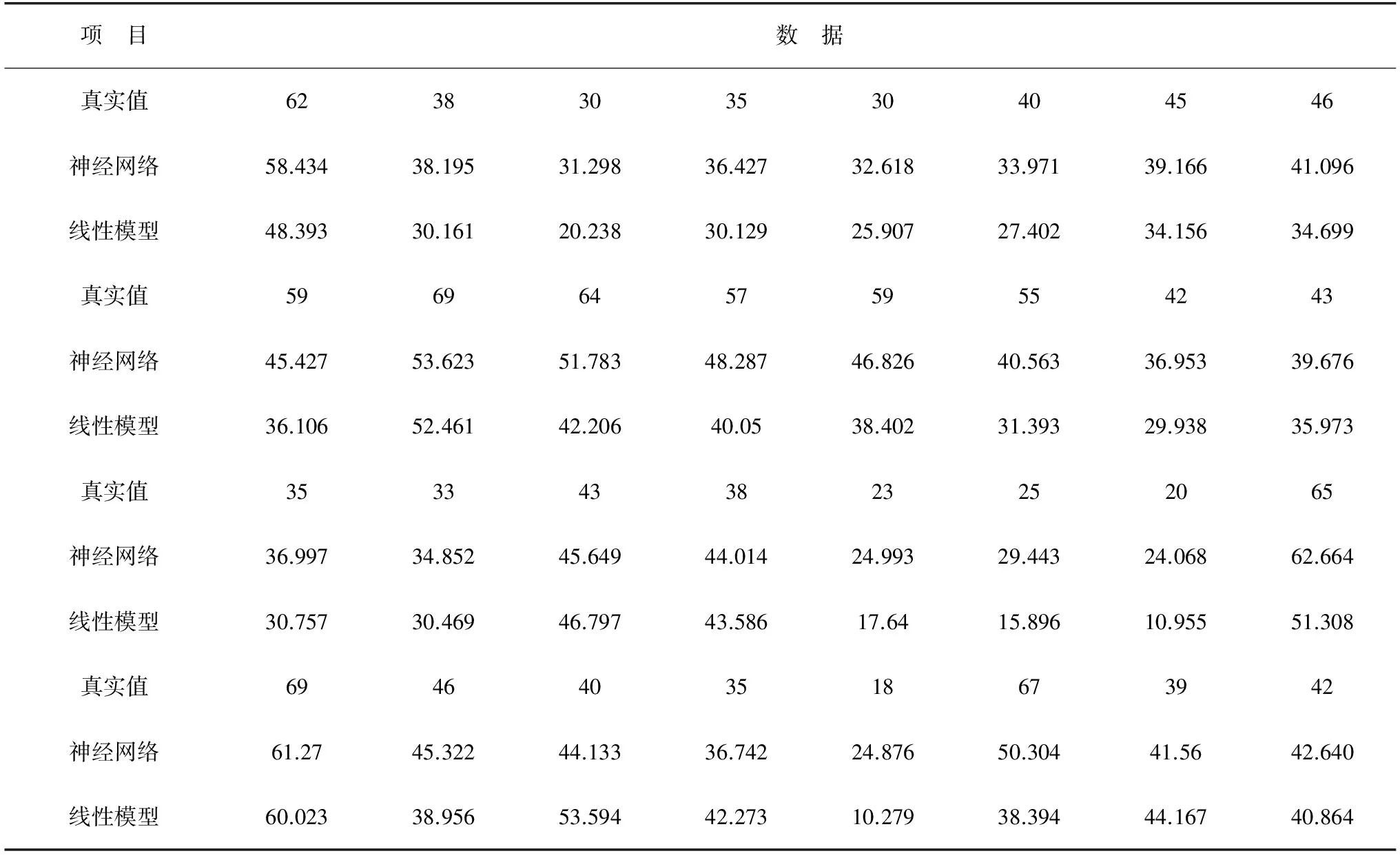
表2 两模型预测值与实际值对比 单位：ug/m3

从表2中可以看出神经网络模型的预测比多元线性回归模型值更接近真实值。最后分别计算出两种模型的残差平方和：多元线性模型残差平方和NRSS1=5 578.06，神经网络模型残差平方和NRSS2=1 972.99。通过综合分析，神经网络模型的拟合效果比多元线性回归模型要好。

5 结 论

通过统计分析对PM2.5的值进行预测，分别运用了神经网络模型和多元线性回归模型。在对神经网络模型的结构确定中，运用了10折交叉验证选取隐层节点数，在此基础上选取出最优的训练周期并运用建立好的神经网模型和多元线性回归模型分别对数据进行拟合。最后通过对两种模型进行比较，结果显示神经网络模型在对PM2.5浓度进行预测的效果远远优于多元线性回归模型。

[1] 刘锋,银利,张星.部分线性模型在空气质量指数细颗粒物PM2.5中的分析应用[J].数学的实践与认识,2014,44(9):130-134

LIU F,YIN L,ZHANG X.Analysis and Application of Partially Linear Model in the Air Quality Index of Fine Particles in PM2.5[J].Mathematics in Practice and Theory,2014,44(9):130-134

[2] 姜新华,薛河儒,张存厚,等.基于主成分分析的呼和浩特市空气质量影响因素研究[J].安全与环境工程,2016,23(1):75-79

JIANG X H,XUE H R,ZHANG C H,et al.Research on the Influencing Factors of Air Quality in Hohhot City Based on Principal Component Analysis[J].Safety and Environmental Engineering,2016,23(1):75-79

[3] 石庆喜,华杰.基于神经网络BP算法的市场预测研究[J].重庆工商大学学报(自然科学版),2004,21(1):69-71

SHI Q X,HUA J.Research on Market Fore-cast Based on Neural Networks Bp Algo-rithms[J].Journed of Technology and Business University(Natural Science Edition),2004,21(1):69-71

[4] 沈路路,王聿绚,段雷.神经网络模型在O_3浓度预测中的应用[J].环境科学,2011,32(8):2231-2235

SHEN L L,WANG Y X,DUAN L.Application of Artificial Neural Networks on the Prediction of Surface Ozone Concentra-tions[J].Environmental Science,2011,32(8):2231-2235

[5] 许兴军,颜钢锋.基于BP神经网络的股价趋势分析[J].浙江金融,2011(11):57-59

XU X J,YAN G F.Stock Price Trend Analys-is Based on BP Neural Network[J].Zhe-jiang Finance,2011(11):57-59[6] 方匡南,吴见彬,朱建平,等.随机森林方法研究综述[J].统计与信息论坛,2011,26(3):32-38

FANG K N,WU J B,ZHU J P,et al.A Revi-ew of Technologies on Random Forests[J].Statistics&Information Forum,2011,26(3):32-38

[7] 毕华,梁洪力,王珏.重采样方法与机器学习[J].计算机学报,2009,32(5):862-877

BI H,LIANG H L,WANG J.Resampling Me-thods and Machine Learning[J].Chinese Journal of Computers,2009,32(5):862-877

[8] 黄文,王正林.数据挖掘:R语言实战[M].北京:电子工业出版社,2014

HUANG W,WANG Z L.Data Mining:Rin Act-ion[M].Beijing:Electronic Industry Publishing House,2014

责任编辑：田 静

Application of Machine Learning to Air Quality Index

LIU Feng1, LI Chun-yan1, TAN Xiang-yong2, WANG Peng-fei1

(1. School of Mathematics and Statistics, Chongqing University of Technology, Chongqing 400054, China; 2. School of Statistics and Management, Shanghai University of Finance and Economics, Shanghai 200433, China)

This paper uses machine learning and multivariate linear regression model to study air quality index of Xian City in nearly one year, firstly uses random forest philosophy to complete the data, then uses cross-validation on the neural network model to select the optimal number of hidden layer nodes and iterations, and finally by comparing the fitting effect of the two models, finds that neural network model is significantly better than multivariate linear regression model for the prediction effect of air quality index.

neural network; multivariate linear regression model; air quality index

10.16055/j.issn.1672-058X.2017.0003.015

2016-09-12；

2016-10-18. * 基金项目：国家自然科学基金项目资助(11471060).

刘锋(1973-),男,湖北新化人,博士,副教授,从事非参数统计研究.

O141.4

A

1672-058X(2017)03-0082-06