基于混合遗传算法求非线性二阶两点边值问题的数值解*
2017-06-19王芳
王 芳
(忻州师范学院 数学系,山西 忻州 034000)
基于混合遗传算法求非线性二阶两点边值问题的数值解*
王 芳
(忻州师范学院 数学系,山西 忻州 034000)
针对非线性二阶两点边值问题,构造了一种基于实数编码的混合遗传算法,将遗传算法和Levenberg-Marquardt算法进行了组合;由于前者全局优化能力强,后者有较强的局部优化能力,故改进后的算法不仅具有全局优化能力,计算的精度不会受到初始取值的影响,并且计算时间少,可以有效提高算法的收敛速度;最后,通过改进后的算法计算非线性二阶两点边值问题解析解和精确解的对比分析表明,该算法对非线性二阶两点边值问题计算有较大的优势,是一种有效的求数值解方法。
实数编码混合遗传算法;二阶边值问题;数值解
在微分方程中,非线性二阶两点边值问题是其研究领域重要和活跃的一个分支。许多学者研究了非线性微分方程边值问题正解的存在性[1-4],大多数文献都仅证明了解的存在性,由于边值问题的解析解的求解难度较大,对于如何求解并未提及。现阶段,求二阶两点边值问题数值解的方法有:有限差分法、打靶法和遗传算法[5]等。其中有限差分法一般仅适用于线性问题;打靶法主要思路是恰当选择和调整初值的条件,对一系列初值问题进行求解,使其接近给定的边界条件。因此,如何采用一种计算精度不受初始取值影响的全局寻优算法对于求非线性二阶两点边值问题是十分必要的。由此,本文构造了一种具有全局优化能力的混合遗传算法,并利用算例检验了模型和算法的有效性和稳健性,为非线性二阶两点边值问题数值解提供了新思路。
1 问题描述
二阶两点边值问题表示为
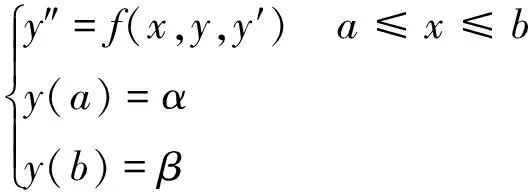
(1)
将上述二阶两点边值问题转换为求最优解的问题,分两步进行。
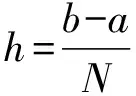
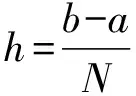
(2)
(3)
则方程(1)的离散格式为
(4)
定义内部节点的残差为
(5)
全体节点的残差为
(6)
记y(xi)为二阶两点边值问题的数值解,当残差R的值越小时,方程(1)的y(xi)就越好。因此,求二阶边值问题的数值解问题就转换为求下面的优化问题:
(7)
其中,f为优化准则函数;X为目标函数的N维向量。
2 实数编码混合遗传算法设计
遗传算法(Genetic Algorithm,GA)[6-13]是一种优化算法,具有全局优化能力,其搜索最优解的原理是模仿自然界的选择与遗传机理。由于遗传算法具有较差的局部搜索能力以及在进化后期其搜索效率也比较低,基于此,将该算法做了改进,即引入Levenberg-Marquardt优化算法作为遗传算法的一个算子,遗传算法的收敛速率是通过Levenberg-Marquardt优化算法具有较强的局部优化能力来提高,组合之后,达到两种算法所具有的全局优化性能和高效局部优化能力,以下为主要步骤。
2.1 编码方案
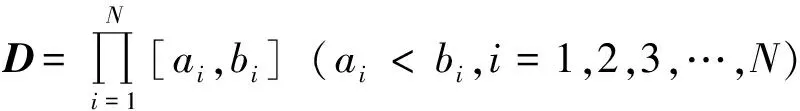
x(i,j)=xmin(i)+y(i,j)(xmax(i)-
(8)
其中,xmax(i),xmin(i)为参数x(i)的上下限,i为节点的值,j为群体中个体的序号。
2.2 初始化
均匀随机数生成的个数是NPOP组,其定义在[0,1]区间。每个组有N个{u(i,j)},将各u(i,j)作为初始群体的父代个体值y(i,j),把y(i,j)代入式(8)得x(i,j),再通过式(7)得到相应的目标函数值f(j)。把{f(j)}(j=1,2,3,…,N)排序,对应的个体{y(i,j)}也跟着排序。这时,确定出最好的个体{y(i,j)}。
2.3 适应值的获取
个体{y(i,j)}的适应度值记作f(j)值。将f(j)值转化为F(j),F(j)表示父代个体的适应度函数值。定义如下:
(9)
2.4 构造选择算子
采用比例选择方式,进行选择操作产生第1代子个体{y1(i,j)}。
2.5 构造交叉算子
双亲是随机选择父代个体y(i,j1)和y(i,j2), 此时,进行随机线性组合,一个子代个体y2(i,j)产生:
(10)
其中,u1,u2,u3是[0,1]区间上的随机数。通过这样的杂交操作,共产生NPOP个子代个体。
2.6 构造变异算子
采用文献[9-12]的方法,NPOP个随机数以pm(j)的概率来代替个体y(i,j),从而得到第3代个体y3(i,j), 即
(11)
其中,u(i)(i=1,2,3,…,p)、um均为[0,1]区间上随机数。
2.7 构造Levenberg-Marquardt算子
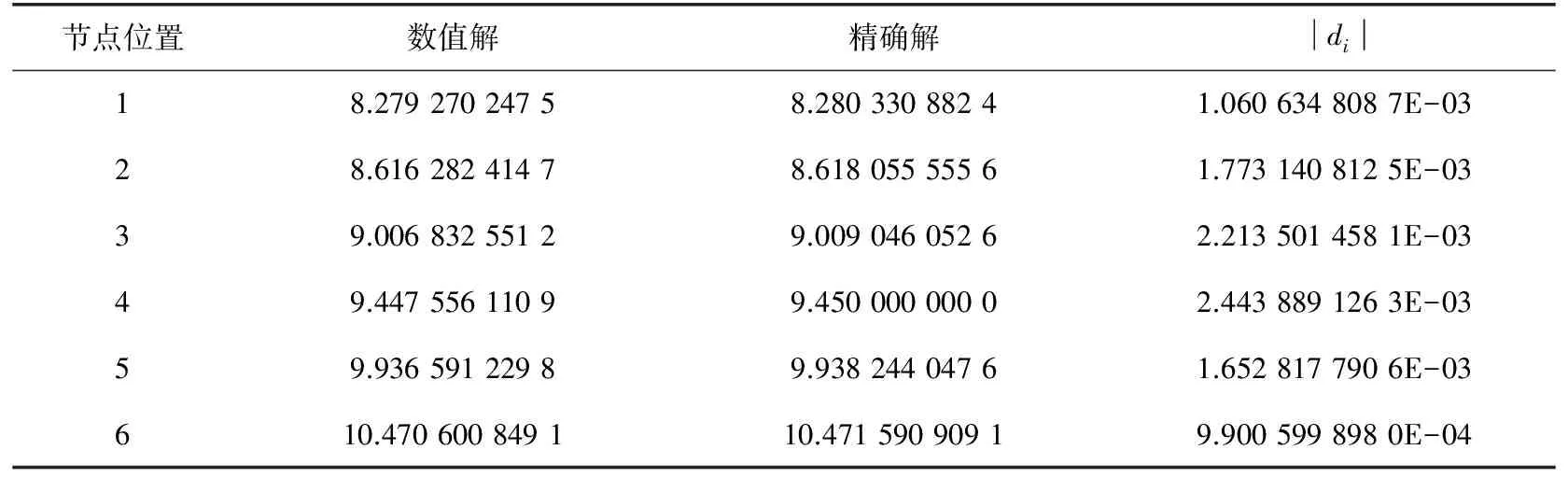
由上面的构造可以得到3NPOP个子代个体,对父代群体中的每一个个体以概率ps(j)进行局部收敛因子Levenberg-Marquardt算子操作,即对父代个体y(i,j),随机生成[0,1]中的随机数pl,若pl(j) 反之,若pl(j)≥ps(j),以y(i,j)为参数的初始取值,直接采用Levenberg-Marquardt算法[9-12]进行优化计算得到y*(i,j)(i=1,2,3,…,N),并计算个体y*(i,j)适应度函数值F*(j),若F*(j)>F(j)则y4(i,j)=y*(i,j),反之y4(i,j)=y(i,j)。 2.8 终止准则 以{y4(i,j)}看作新一代父代群体,算法重新对父代群体依前面的步骤进行循环演化。若最好的个体的目标函数值小于设定值或算法运行达到预定循环次数时,则进化结束。保存当前群体中最好的个体或者其最好个体的平均值为结果。 用文中构造的算法求解非线性二阶两点边值问题: (12) 表1 数值解、精确解以及误差 由表1中的数值结果可知,本文构造的新的混合遗传算法对非线性二阶两点边值问题进行优化求解是可行的。从计算结果看,该算法充分发挥了遗传算法的全局优化能力和Levenberg-Marquardt算法的局部优化能力,因此,可广泛应用于各类非线性二阶边值问题,是一种较理想的计算方法。 [1] LIAN W C,WONG F H,YEH C C.On the Existence of Positive Solutions of Nonlinear Second Order Differential Equations[J].Journal of AMS,1996,124(6):1117-1126 [2] ERBE L H,H U S,WANG H.Multiple Positive Solutions of Some Boundary Value Problems[J].Journal of Mathe-matical Analysis & Applications,1994,184:640-648 [3] LIU Z,LI F.Multiple Positive Solutions of Nonlinear Two- point Boundary Value Problem[J].Journal of Mathematical Analysis & Applications,1996,203(5):610- 625 [4] LEES M.Diserete Methods for Two-point Boundary Value Problems,Numerical Solutions of Partial Differential Equations[J].New York:Academic Press,1966 [5] BASKAR S,SUBBARAJ P,RAO M V C.Hybrid Real Coded Genetic Algorithm Solution to Economic Dispatch Problem[J].Computers and Electrical Engineering,2003,29(3):407-419 [6] GOLDBERGD E.Genetic Algorithms in Search,Optimi-zation and Machine Learning[M].New York:Addison-Wesley,1989 [7] BACK T.Evolution Strategies:an Alternative Evolutionary Algorithm[C]∥Artificial Evolution:European Conference Selected Papers,Berlin,1995:1-20 [8] MARQUARDT D W.An Algorithm for the Solution of Certain Nonlinear Inequalities[J].Journal of Applied Math,1963(11):431-441 [9] 王芳,杨虎山.实数编码混合遗传算法在参数估计中的应用[J].高等学校计算数学学报,2013,35(4):375-383 WANG F,YANG H S.Application of Parameter Estimation Based on Real Coded Hybrid Genetic Algorithm[J].Numerical Mathematics a Journal of Chinese Universities,2013,35(4):375-383 [10] 郭向红,孙西欢,马娟娟.基于混合遗传算法估计van Genuchten方程参数[J].水科学进展,2009(5):677-681 GUO X H,SUN X H,MA J J.Parametric Estimation of the Van Genuchten’s Equation Based on Hybrid Genetic Algorithm[J].Advances in Water Science,2009(5):677-681 [11] 金菊良,杨晓华,丁晶.基于实数编码的加速遗传算法[J].四川大学学报,2000(4):20-24 JIN J L,YANG X H,DING J.Real Coding Based Acceleration Genetic Algorithm[J].Journal of Sichuan University (Engineering Science Edition),2000(4):20-24 [12] 王芳,杨虎山.基于LM算法和遗传算法求解非线性方程组[J].忻州师范学院学报(自然科学版),2016(5):19-21 WANG F,YANG H S.Based on the LM Algorithm and Genetic Algorithm for Solving Non-linear Equations[J].Xinzhou Teachers University (Natural Science Edition),2016(5):19-21 [13] 王芳.一种混合遗传算法的收敛性分析[J].九江学院学报(自然科学版),2016(3):84-85 WANG F.Convergence Analysis of a Hybrid Genetic Algorithm[J].Journal of Jiujiang University (Natural Science Edition),2016(3):84-85 责任编辑:罗姗姗 Numerical Solution to Nonlinear Second-order Two-point Boundary Value Problem Based on Hybrid Genetic Algorithm WANG Fang (Department of Mathematics,Xinzhou Normal College, Shanxi Xinzhou 034000, China) According to nonlinear second-order two-point boundary problem, a hybrid genetic algorithm based on real coding is constructed by the combination of the genetic algorithm with Levenberg-Marquardt algorithm. Because the former has the advantages of global optimization ability while the latter has strong local optimization ability, therefore, the improved algorithm not only has global optimization ability but also the calculation accuracy can not be affected by initial values, can use less computing time, and can effectively improve the convergence speed of the algorithm. Finally, the comparison between analytical solution and exact solution to nonlinear second-order two-point boundary value problems by using the improved algorithm indicates that the improved algorithm has big advantages of nonlinear second-order two-point boundary value problems computation and is an effective method for numerical solution. real coded hybrid genetic algorithm; second-order boundary value problem; numerical solution 10.16055/j.issn.1672-058X.2017.0003.002 2016-12-10; 2017-01-15. * 基金项目:忻州师范学院青年基金(QN201316). 王芳(1978-),女,河南焦作人,讲师,硕士,从事应用数学研究. O241.8 A 1672-058X(2017)03-0007-043 实例分析
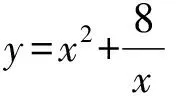
4 结 论
