一类具有随机扰动的传染病SEIR模型稳定性分析

徐 敏, 胡良剑, 丁永生

(1.上海对外经贸大学 商务信息学院, 上海 201620；2.东华大学 a. 理学院; b. 信息科学与技术学院, 上海 201620)

一类具有随机扰动的传染病SEIR模型稳定性分析

徐 敏1, 胡良剑2a, 丁永生2b

(1.上海对外经贸大学 商务信息学院, 上海 201620；2.东华大学 a. 理学院; b. 信息科学与技术学院, 上海 201620)

考虑疾病传播过程中的随机干扰, 运用随机人口建模中参数扰动的标准化技术, 建立了一类具有随机扰动的传染病SEIR(susceptible-exposed but not infectious-infectious-removed)模型, 证明了模型解的存在唯一性及非负性, 并研究了无病平衡点满足p阶矩指数稳定的条件.研究结果为传染病预防与控制提供一定的理论依据与决策支持.

随机扰动; SEIR模型; 无病平衡点;p阶矩指数稳定性

1927年, 文献[1]报道了著名的SIRS(susceptible-infective-removed-susceptible)模型, 用于传染病传播过程的建模, 并将人群分成3类, 即易感者(susceptible)、感染者(infective)和移出者(removed).这类模型适用于疾病无潜伏期的情况, 然而, 对大部分传染病而言,从感染到发病需要一段时间, 因此, 具有潜伏期的传染病的传播可以用SEIR(susceptible-exposed but not infectious-infectious-removed)模型建模, 近年来, 有大量学者对传染病SEIR模型进行研究.文献[2]研究了一类具有年龄依赖潜伏期和复发的SEIR模型的全局渐近稳定性; 文献[3]研究了一类具有非线性发病率的SIR(susceptible-infectious-removed)和SEIR模型的动力学行为; 文献[4]研究了一类具有一般发病率的非自主性SEIRS(susceptible-exposed but not infectious-infectious-removed-susceptible))模型, 得出了疾病灭绝的条件.文献[5]得到了一类SEIR模型的解析解, 通过仿真对该模型的精确解和解析解进行对比.疾病的传播一般会受到随机因素的干扰, 基于此, 文献[6]建立了一类带有无限时滞的两群组的随机SEIR模型, 得到了其渐近稳定性的条件并进行了仿真.文献[7]建立了一类带跳的随机SEIR模型, 研究了解的渐近稳定性.文献[8]建立了一类具有独立随机扰动的SEIR模型, 证明了其无病平衡点的几乎必然指数稳定性.文献[9]研究了一类具有随机扰动的多群组的SEIR模型.文献[10]建立了一类带有随机扰动的多群组SEIR模型和SIR模型, 并研究了其随机渐近稳定性.在考虑到疾病的传播率受到环境因素的干扰下, 文献[11]建立了一类带有环境噪声干扰的随机SEIR模型, 并证明了其全局渐近稳定性.

本文对文献[11]中的随机SEIR模型补充证明了其解的存在唯一性以及非负性, 进一步得到了该模型的平凡解p阶矩稳定性的条件, 为具有潜伏期的传染病预防及控制提供一定的理论依据与决策支持.

1 随机SEIR模型的生成

不失一般性, 设t时刻总人口数为N(t), 假设不考虑人口的迁移, 令N(t)=N,S(t)表示t时刻未染病但有可能被疾病传染的人数占总人口数的比例,I(t)表示t时刻已被传染成病人而且具有传染力的人数占总人口数的比例.病人在被感染后成为患病者之前有一段病菌潜伏期, 假定在潜伏期内的感染者没有传染力, 记t时刻潜伏者人数占总人口数的比例为E(t),R(t)表示t时刻已从染病者康复的人数占总人口数的比例, 并假定病人康复后具有永久免疫力.考虑一类具有常数移民的SEIR传染病模型:

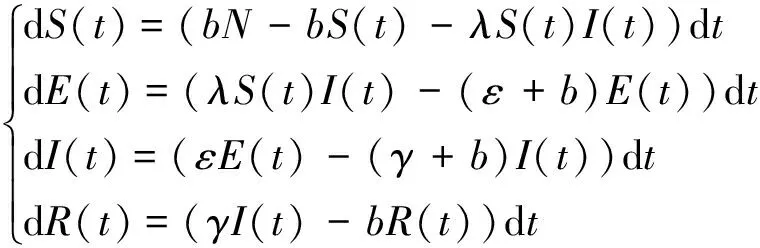
(1)

假设总人口恒定, 即在疾病流行期间, 考虑人口的出生与自然死亡等变化, 假定出生率(单位时间内出生的人数在总人数中的比例)与死亡率相等, 用b表示,λ表示疾病传播率, 疾病的平均潜伏期为1/ω,γ表示病人康复后退出系统的移出率.对该确定性的SEIR模型而言, 文献[12]得出了疾病再生数R0为

(2)

当R0≤1时, 无病平衡点P0(N, 0, 0, 0)全局渐近稳定; 当R0>1时, 无病平衡点P0(N, 0, 0, 0)不稳定.考虑疾病传播过程中环境因素的干扰, 将环境噪声引入模型, 考察其解的特性, 利用随机人口建模中的标准技术, 假设疾病传播率λ受到环境因素的干扰, 假设噪声的干扰强度为σ, 用λ+σdωt代替λ, 得到一类随机SEIR模型如下:

dS((t)=(b-bS(t)-λS(t)I(t))dt-σS(t)I(t)dωt

(3)

dE(t)=(λS(t)I(t)-(ε+b)E(t))dt+

σS(t)I(t)dωt

(4)

dI(t)=(εE-(γ+b)I)dt

(5)

dR(t)=(γI-bR)dt

(6)

ωt是一维纳过程(布朗运动), 故满足

Eωt=0,Dωt=1

2 解的非负性

引理1 如下不等式成立:

u≤2(u+1-log(u))-(4-2log2), ∀u>0

证明： 对∀u>0定义函数

f(u)=u+2-2log(u)

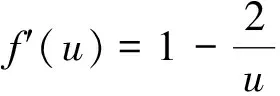
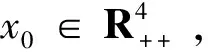
证明： 根据已知E(t)≥I(t), 则由式(5)得:

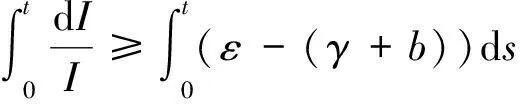
于是

音乐作为人们内心世界的隐喻，或者说作为人的内在情感的某种外化，它能够把人的各种情感形态隐喻地表现出来（王炳社，2013）。但音乐的听觉隐喻性及其表达方式在国内一直没有得到学者的重视。戴维斯划分音乐为悲伤和快乐两种类型，音乐的“悲伤”等修饰语也属于情感的隐喻表达。Grey认为音乐隐喻有两种模式：叙事模式和图画式的视觉模式。叙事模式关注叙事方式和结构过程、叙事情境和叙事风格。音乐叙事的目的是使听者能在较深的层面对音乐意涵有较为理性的感悟。宋瑾（2011）认为音乐的技术术语中也有感觉术语和情感术语，感觉术语如演奏中的“快速”“中弱”等，情感术语如“抒情地”“忧郁地”等等，这些都具有音乐隐喻性。

I(t)≥I(0)·e(ε-(γ+b))t>0 a.s.

同理, 由于I(t)≥R(t), 由式(6)得:

R(t)≥R(0)·e(γ-b))t>0 a.s.

下证对∀t≥0,S(t)>0,E(t)>0 a.s.

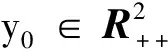
τk=inf{t∈[0, τe): S(t)∉(1/k, k)

orE(t)∉(1/k, k)}

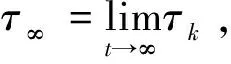
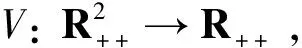
V(x)=S(t)+1-logS(t)+E(t)+1-logE(t)

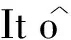
dV(y(t))≤(c1+λE(t))dt+σNdωt

由引理1和V的定义可知,E(t)≤2V(x)-(4-2log2), 于是有

dV(y(t))≤(c2(1+V(x)))dt+σNdωt

于是

EV(y(τk∧t1))≤V(y0)+c2T+

根据Gronwall不等式,EV(y(τk∧T))≤c3,c3=(V(y0)+c2T)ec2T, 对k≥k1, 令P(Ωk≥ε), 则P(Ωk≥ε), 于是

V(y(τk,ω))≥[k+1-log(k)]∧[(1/k)+

1+log(k)],

由Ωk的定义可知c3≥E[1Ωk(ω)V(y(τk,ω))]≥ε([k+1-log(k)]∧[(1/k)+1+log(k)])

令k→∞, 得∞>c3=∞, 矛盾, 于是τ∞=∞ a.s.

3 指数稳定性

笔者已得出模型(3)～(6)的解全局渐近稳定性的条件[11], 更进一步, 这里讨论方程(3)～(6)的平凡解的p阶矩指数稳定性.不失一般性, 在[0, ∞)上具有初始值x(0)=x0的d维随机微分方程为:

dx(t)=f(x(t),t)dt+g(x(t),t)dωt

(7)

假定对∀t≥t0,f(0,t)=0,g(0,t)=0, 则对应于初始条件x(t0)=0, 方程(7)有解x(t)≡0, 该解称为平凡解或平衡位置.

定义1[13]若存在一对正数λ和C使得对∀t≥0,E|x(t;x0)|p≤C|x0|pe-λt, 则称式(7)的平凡解是p阶矩指数稳定的.

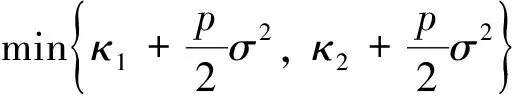
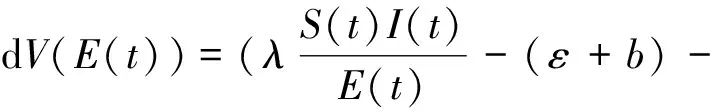
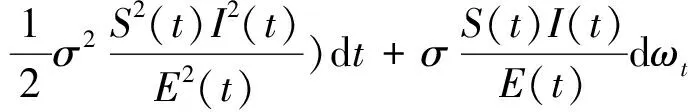
两边从0到t积分, 得

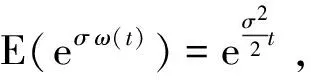
则对任何正整数p, 有

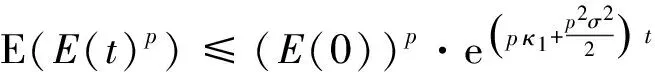
同上可得,

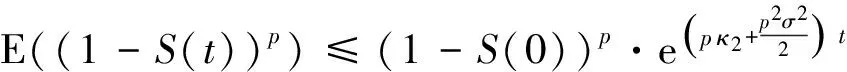
其中κ2=λ-b, 根据定义1及已知条件可知, 定理2成立.

4 结 语

[1] KERMACK W O, MCKENDRICK A G. Contributions to the mathematical theory of epidemics[C]//Proceedings of the Royal Society of London. 1927: 700-721.

[2] LIU L L, WANG J L, LIU X N.Global stability of an SEIR epidemic model with age-dependent latency and relapse[J]. Nonlinear Analysis(Real World Applications), 2015, 24: 18-35.

[3] LIU J L, PENG B Y, ZHANG T L.Effect of discretization on dynamical behavior of SEIR and SIR models with nonlinear incidence[J]. Applied Mathematics Letters, 2015, 39: 60-66.

[4] MATEUSA J P, SILVA C M.A non-autonomous SEIRS model with general incidence rate[J]. Applied Mathematics and Computation, 2014, 247: 169-189.

[5] WANG X Y, WEI L J, ZHANG J. Dynamical analysis and perturbation solution of an SEIR epidemic model[J]. Applied Mathematics and Computation, 2014, 232: 479-486.

[6] LIU M, BAIA C Z, WANG K. Asymptotic stability of a two-group stochastic SEIR model with infinite delays[J]. Communications in Nonlinear Science and Numerical Simulation, 2014, 19(10): 3444-3453.

[7] ZHANG X H, WANG K.Stochastic SEIR model with jumps[J]. Applied Mathematics and Computation, 2014, 239(15) : 133-143.

[8] WITBOOI P J. Stability of an SEIR epidemic model with independent stochastic perturbations [J]. Physica A: Statistical Mechanics and its Applications, 2013, 392(20): 4928-4936.

[9] YANG Q S, MAO X R. Extinction and recurrence of multi-group SEIR epidemic models with stochastic perturbations [J]. Nonlinear Analysis: Real World Applications, 2013, 14(3): 1434-1456.

[10] YUAN C J, JIANG D Q, O’REGAN D, et al. Stochastically asymptotically stability of the multi-group SEIR and SIR models with random perturbation [J]. Communications in Nonlinear Science and Numerical Simulation, 2012, 17(6): 2501-2516.

[11] XU M, HU L J.Global asymptotic stability of an SEIR model with random perturbation [J]. Journal of Donghua University (English Edition), 2014, 31(2): 152-154.

[12] LI M Y, GRAEF J R, WANG L, et al. Global dynamics of a SEIR model with varying total population size[J], Mathematical Biosciences, 1999, 160(2): 191-213.

[13] MAO X R.Stochastic differential equations and applications[M]. Chichester: Ellis Horwood, 1997: 206-212.

(责任编辑: 徐惠华)

Stability Analysis of Solution for an Epidemics SEIR Model with Random Perturbation

XUMin1,HULiangjian2a,DINGYongsheng2b

(1.Business Information Management School, Shanghai University of International Business and Economics,Shanghai 201620, China; a. College of Science; b. College of Information Science and Technology,2.Donghua University, Shanghai 201620, China)

Stochasticity is introduced into an epidemics SEIR(susceptible-exposed but not infectious-infectious-removed) model via the technique of parameter perturbation which is standard in stochastic population modeling. The existence and uniqueness are also proved for the solution. The model possessing non-negative solutions established are also proved as desired in any population dynamics. And the condition is obtained for the trivial solution of the model to be p-th moment exponential stable. In this way, theoretical foundation and decision support is provided for epidemics’ prevention and control.

random perturbation; SEIR(susceptible-exposed but not infectious-infectious-removed) model; disease free equilibrium;p-th moment exponential stability

1671-0444 (2017)02-0305-04

2016-02-23

教育部人文社会科学基金资助项目(15YJCZH2010)；上海市教委创新资助项目(14YZ134)；上海市高校085资助项目

徐 敏(1980—)，女，安徽安庆人，副教授，博士，研究方向为随机模型、管理决策和风险管理.E-mail: xumin@suibe.edu.cn

X 43; O 141.4

A