考虑时间维的城市公交专用道布局优化模型*

卢小林 潘述亮 邹难†

(1.山东大学 控制科学与工程学院， 山东 济南 250061； 2.济南全通信息科技有限公司， 山东 济南 250101)

考虑时间维的城市公交专用道布局优化模型*

卢小林1潘述亮2邹难1†

(1.山东大学 控制科学与工程学院， 山东 济南 250061； 2.济南全通信息科技有限公司， 山东 济南 250101)

针对一定规划时段内的城市公交专用道布局方案及时序安排，从公交专用道布设规划与建设实践以及路网需求的动态变化入手，利用网络优化方法提出了考虑时间维的公交专用道网络布局双层优化模型.该模型的上层模型是以最大化路网消费者剩余为目标的公交专用道网络布局设计决策，下层模型是以最小广义出行成本为目标的小汽车和公交车客流分配模型，并用遗传算法求解.文中还通过算例分析验证了该双层优化模型的有效性与实用性，以及考虑时间维的专用道网络布局方案相较于单一分阶段公交专用道布局方案的优越性.结果表明，文中建立的模型能够同时优化公交专用道的布局方案及建设时序.

公共交通；公交专用道；时间维；双层规划模型；遗传算法

近年来，城市机动化交通需求的持续增长引发了交通拥堵、环境污染等一系列交通问题.在此情况下，实施公交优先发展策略已经成为解决城市交通发展问题的重要策略之一.公交专用道作为公交优先措施之一，通过为公交车提供专用道路空间，可以有效提升公交车通行效率，引导小汽车使用者向公交车出行转移.国内外已有众多学者对公交专用道布局方法进行研究，现有研究成果可以分为两类：①微观仿真模拟[1-5]；②宏观网络优化[6-12].前者侧重于使用仿真工具评估某一条公交专用道布设方案的效益，如专用道对公交车用户和小汽车用户出行时间以及道路饱和度的影响等，来判断公交专用道布设方案的可行性与合理性；后者主要是利用双层规划模型求解公交专用道的最优网络布局.模型通常以路网用户总出行时间最小为目标，兼顾公交方式的出行分担率、污染排放、事故等因素，结合一定的路网拓扑条件，从网络层面确定公交专用道的最优布局方案.

因受限于资金以及兼顾道路基础设施建设项目对城市路网运行特性的影响，城市道路基础设施建设项目往往不是一蹴而就，而是根据动态需求进行分时段的规划建设.近年来，少数研究已经在城市交通网络设计问题中考虑了时间变化对路网改善策略的影响，这也在路网设计问题中产生了考虑时间维的研究分支.Lo[13],Szeto等[14-15]以消费者剩余最大化为目标，研究了基于时间维的网络规划问题，设计决策包括道路收费、车道拓宽等；Szeto等[16]进一步考虑土地经济效益对基于时间维的离散路网设计影响等问题；孙强等[17]提出了需求不确定条件下的多阶段综合交通网络规划问题，考虑了分年度交通基础设施建设与交通需求的协调发展.分时段实施策略也同样适用于公交专用道建设.然而，目前大多数研究中通常将公交专用道作为静态要素，而忽略了由城市交通需求动态变化而引起的城市公交专用道的分时段同步优化问题.

文中借鉴网路优化模型中的分时段设计思路，引入“时间维”概念并将其应用到公交专用道布局设计问题中，从宏观网络优化层面构建考虑时间维的公交专用道网络布局优化模型，以期为分时段的公交专用道有序建设和衔接提供决策支持，并最大化公交专用道效益.同时，考虑公交专用道的现实建设条件与管理需求(如设置专用道所需的道路条件等)，真实刻画不同客流需求条件下专用道网络布局与路网运行特性之间的关系.

1 问题描述

为考虑路网的动态特性，以及用户路径的随机分配和弹性需求的影响，选择消费者剩余最大化(CS)为优化目标.路网中考虑小汽车和公交车两种交通模型的影响.文中将构建双层规划模型，以路网拓扑结构、道路特性、公交线网路径及发车频率、起止(OD)弹性需求等为基本输入，上层模型设计为分时段的公交专用道布局决策模型，下层模型设计为小汽车和公交车客流分配模型.同时，为了真实刻画公交专用道现实建设条件与管理需求，在上层模型中加入道路条件以及投资成本等条件约束.特别强调的是，为了使得优化方案具备可落地性，模型限定实施公交专用道的道路饱和度约束，兼顾公交专用道设置后社会车辆的交通通行效率.

2 模型构筑

2.1 基本假设

为了使研究问题得到简化，并能反映真实情况，提出如下假设：①道路单向允许设置一条公交专用道；②假设规划时间范围内，路网保持不变；③假设每一规划时段内，路网需求保持不变；④已知分年度的投资成本约束；⑤出行者的路径选择行为遵循广义出行费用最小化的用户均衡原则.

2.2 模型参数

模型中涉及的定义及参数如表1所示.

表1 数学模型中各参数和变量的含义

Table 1 Notation of parameters and variables for the mathema-tical model

集合定义(N,A)道路网络集合,N表示道路网络节点,A表示道路网络的有向弧集(Nb,Ab)公交网络集合,Nb表示公交网络节点,Ab表示公交网络的有向弧E网络所有公交线路集合,e为集合E的索引O,DOD对起、终点集合,o,d分别为O,D索引T路网规划时间范围RcodOD对(o,d)之间的小汽车路径集合,c表示小汽车方式RbodOD对(o,d)之间的公交车路径集合,b表示公交方式决策变量定义δ,ij=10{如果规划时段弧(i,j)设置公交专用道,δ,ij=1,否则为0辅助变量定义δc,rij,od=10{如果弧(i,j)在小汽车路径r上,δc,rij,od为1,否则为0δb,r'ij,od=10{如果弧(i,j)在公交车路径r'上,δb,r'ij,od为1,否则为0yeij=10{如果公交线路e经过弧(i,j),yeij为1,否则为0参数定义路网规划时段Q,od规划时段内OD对(o,d)之间的总出行需求Qc,od规划时段内OD对(o,d)之间的小汽车总出行需求Qb,od规划时段内OD对(o,d)之间的公交车总出行需求B规划时段内路网的改造投资约束u规划时段内公交专用道的单位投资成本nij弧(i,j)的车道数量Oc小汽车乘客占有率Ob公交车额定载客量ω公交车转换为小汽车的车辆折算系数lij弧(i,j)的长度fe公交线路e的发车频率Smax道路交通饱和度的最大约束Cij弧(i,j)单车道通行能力函数定义xc,od规划时段内弧(i,j)的小汽车乘客量(人/时)xb,od规划时段内弧(i,j)的公交乘客流量(人/时)tc,od规划时段内弧(i,j)上小汽车的出行时间tb,od规划时段内弧(i,j)上公交车的出行时间xc,r,od规划时段内OD对(o,d)之间路径r的小汽车流量xb,r',od规划时段内OD对(o,d)之间路径r'的公交乘客量tc,r,od规划时段内OD对(o,d)之间小汽车在路径r的出行时间tb,r',od规划时段内OD对(o,d)之间公交车在路径r'的出行时间CS规划时段内路网消费者总剩余Z目标函数值

2.3 模型表述

2.3.1 上层模型

目标函数

(1)

s.t.

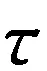
(2)

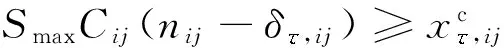
(3)

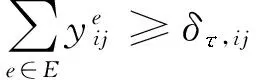
(4)

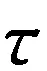
(5)

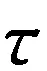
(6)

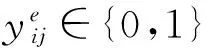
(7)

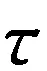
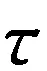
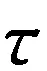
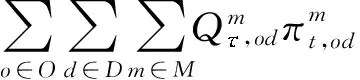
(8)

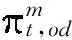
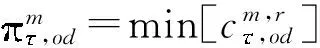
(9)

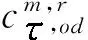
文中考虑OD需求为弹性的，即路网用户出行量受出行成本影响.交通出行量大小反映了路网通行效率，可以表示为

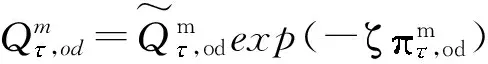
(10)

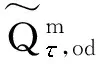
利用式(9)、(10)，可以进一步对式(8)进行转化，得到

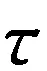
(11)

2.3.2 下层模型

在上层决策者给定公交专用道网络布局方案后，下层模型求解道路网络及公交网络的均衡配流.下层模型由交通模式划分模型、小汽车客流分配模型和公交客流分配模型3个模块组成，其中客流分配采用随机用户均衡(SUE).文中路网出行者可以选择小汽车和公交车两种交通方式出行，且交通方式划分以及路径流量分配可用Logit随机用户平衡分配模型确定.

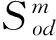
(12)

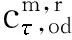
(13)

(14)

(15)

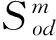
(16)

式中，θ1为随机参数.

对式(16)求偏导数即可推导出基于Logit的路径选择公式：

(17)

出行者对交通方式满足基于最小期望出行阻抗的Logit模型.

(18)

式中，θ2为随机参数[18].

此时混合交通网络平衡条件为式(19)-(21)，其中式(19)为OD对(o,d)的交通方式流量平衡关系，式(20)为OD对(o,d)的交通方式路径流量平衡关系，式(21)定义了路段与经过该路段的交通流的平衡关系.

(19)

(20)

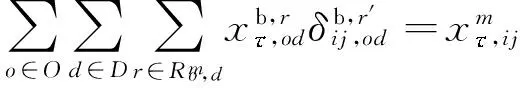
(21)

文中设定每年OD需求量按照规划时段而逐渐增长，可以表示为

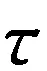
(22)

利用路阻函数计算路段出行时间.

(23)

(24)

根据路段的公交专用道设置情况，可以划分为3种类型：

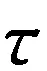
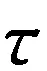
情况3 路段无公交线路经过，此时仅有小汽车通行.

3 模型求解

上述模型为非线性混合整数双层规划问题，属于典型的NP-hard问题，文中将利用基于连续权重平均法(MSWA)的遗传算法(GA)进行模型求解[18-19].

步骤1 GA初始种群编码

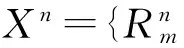
步骤2 交通分配模型求解

利用MSA算法求解交通分配模型，主要包括3个阶段，即交通方式划分、小汽车客流分配、公交车客流分配.内循环为交通方式随机分配模型，外循环为交通方式划分模型.最终得到路网平衡配流结果.

步骤3 计算适应度函数

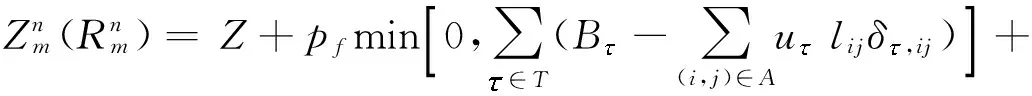
(25)

定义适应度函数：

(26)

通过计算当前方案的适应度函数值与已生成方案中适应度最优相对差值，更新适应度和更新染色体排序，将最终适应度最大的方案作为所求结果.

步骤4 遗传操作

选择操作利用轮盘赌选择法和精英保留策略的组合选择方法，利用个体的适应度函数值确定个体的选择概率，适应度函数值越大的个体被选择向下一代群体繁殖的概率越大.交换操作采用单点交换；变异操作采用单点变异(0变异为1，或将1变异为0).交叉与变异操作后，对新种群进行可行性处理，生成下一代新群体，并转到步骤5.

步骤5 终止判断

判断是否到达最大迭代次数，或者判断是否满足收敛约束：

(27)

如果满足收敛约束或者达到最大迭代次数，则输出种群中适应度最高的染色体为最优解，循环结束，否则返回步骤1.

4 算例分析

利用SiouxFalls网络[20]分析实验结果，验证所建模型的有效性.该网络由24个节点、76条有向路段以及7条公交线路构成.如图1所示.

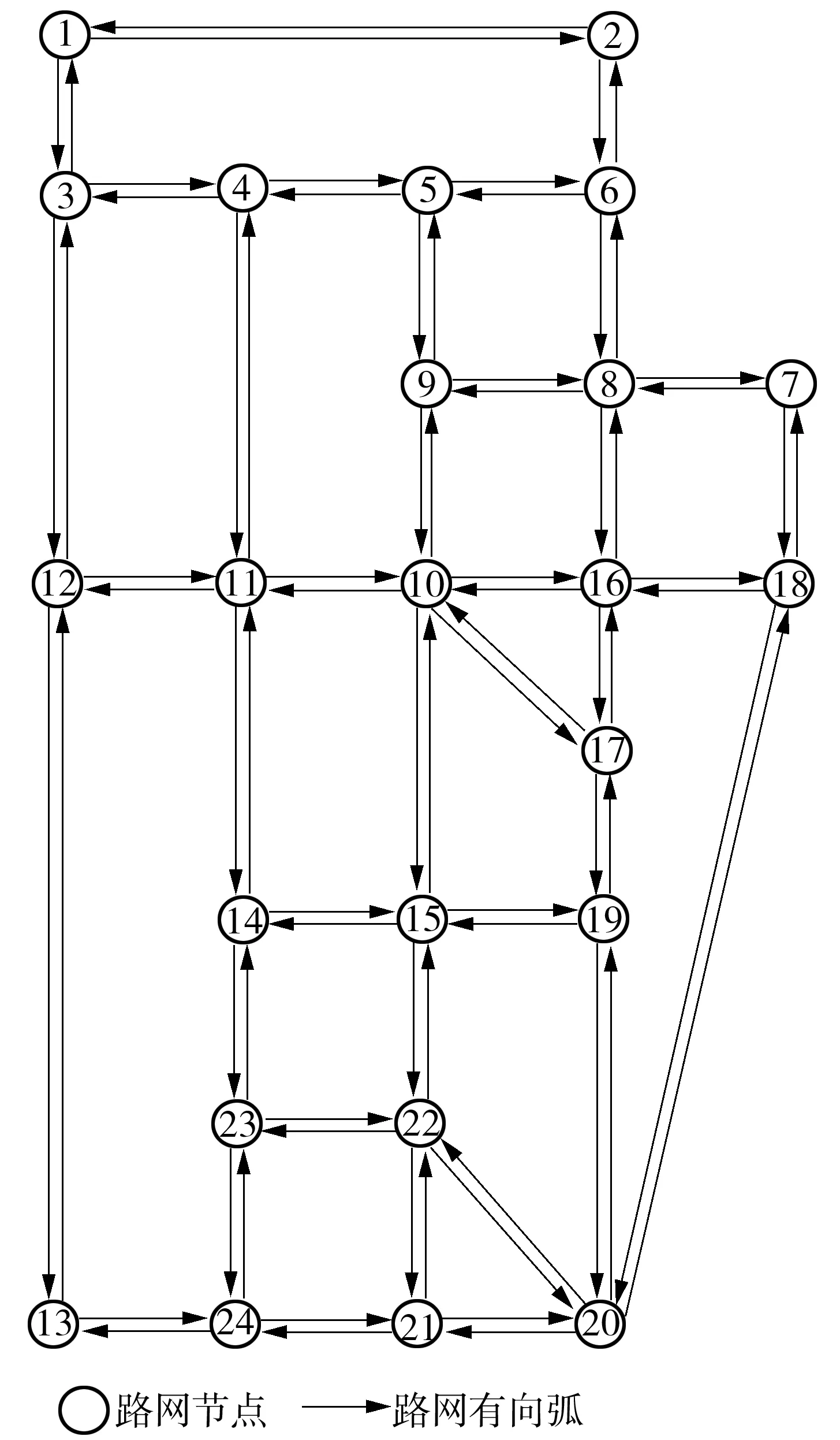
图1 测试路网

4.1 模型输入与输出

4.1.1 模型输入

模型输入包括以下几个方面.

1)模型涉及的参数值，见表2.

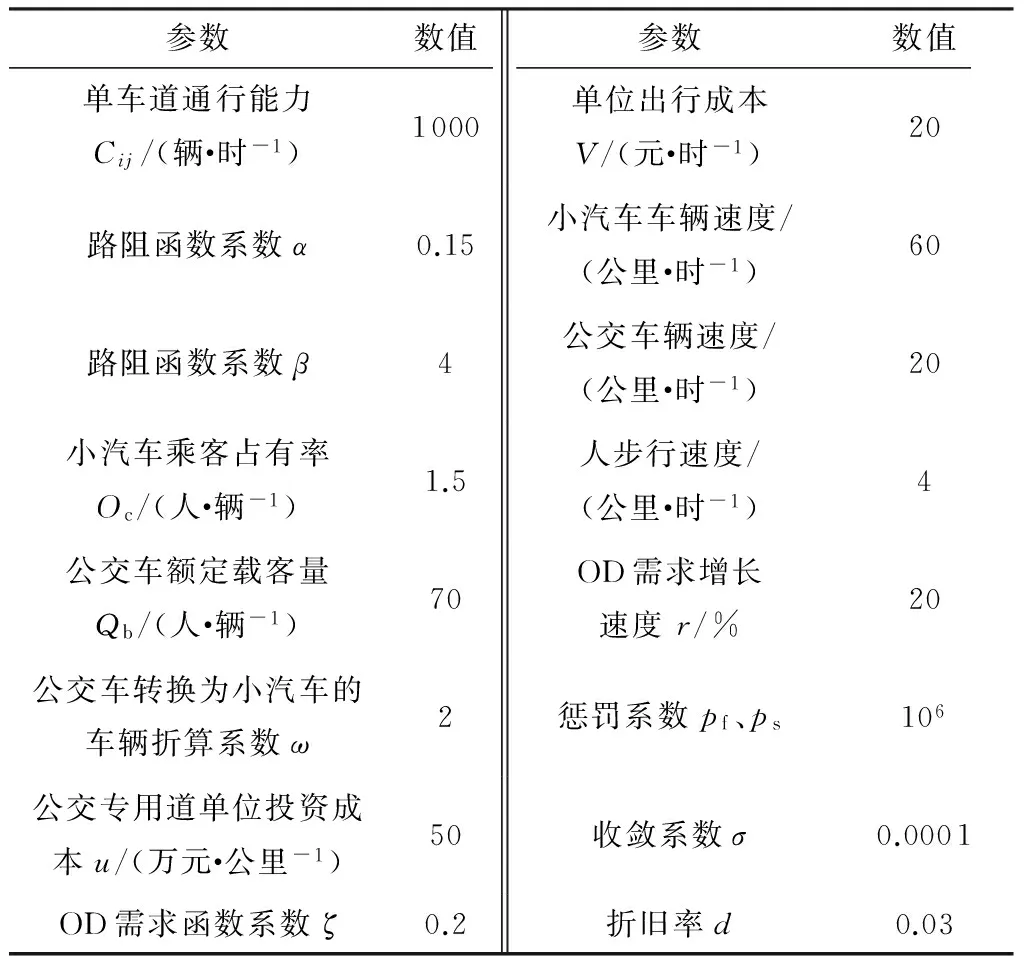
表2 模型涉及的输入参数值

2)路网所有道路的基本特性，包括自由流出行时间、长度、每个方向的车道数量以及其他与路阻函数相关的基本参数值，如表3所示.

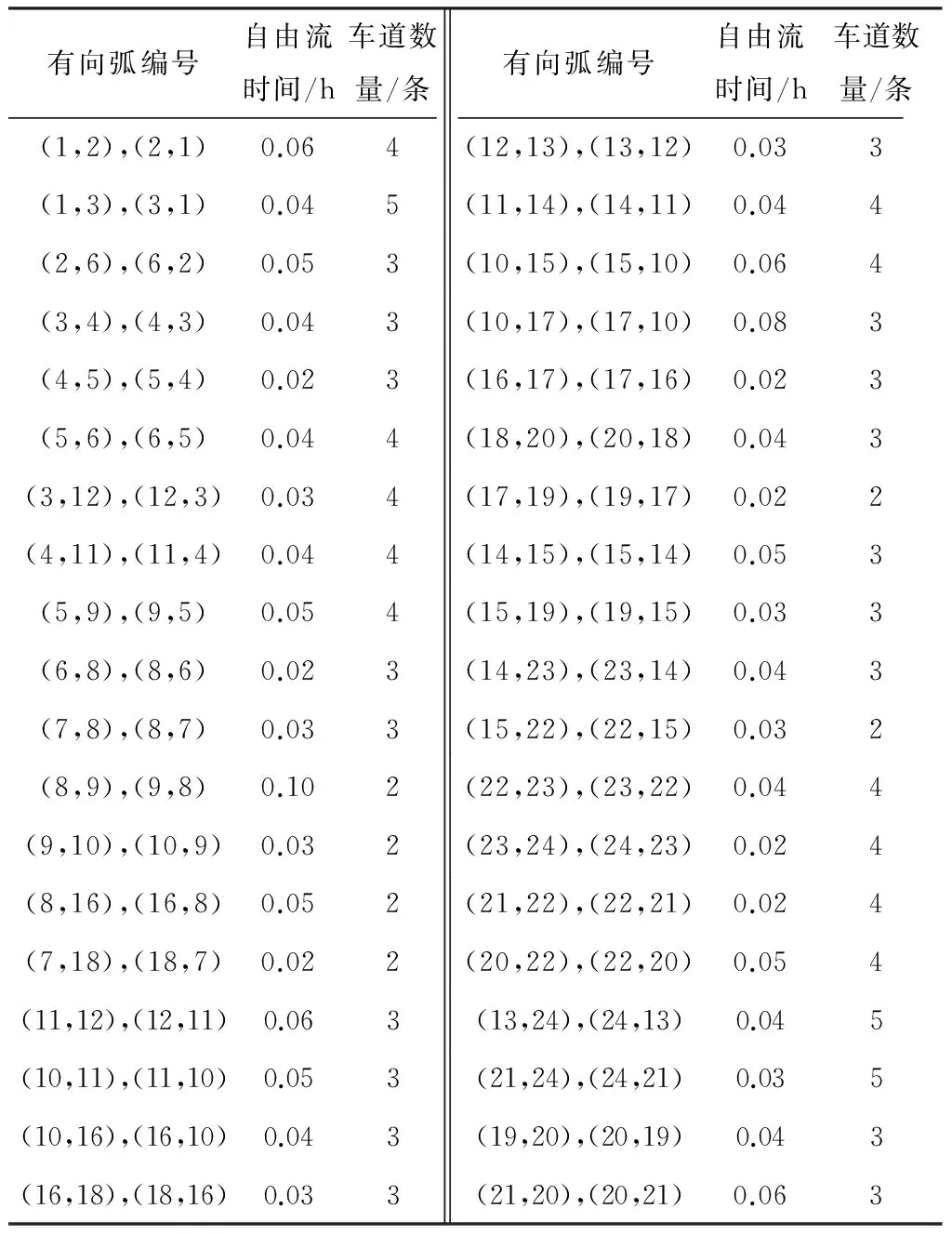
表3 路段基本特性

3)每个OD对之间的高峰小时出行需求(包括公交车与小汽车)，如表4所示.

4)公交线路路径及发车频率，如表5所示.

4.1.2 模型输出

模型输出采用分时段的公交专用道最优布局方案.4.2 优化结果分析

使用Matlab R2012对文中的模型进行编程，将表2-5数据代入模型对该数值案例求解，并根据路网规模以及公交专用道的投资成本，设定3个规划时段划分，对应的投资计划分别为2 000万元、4 000万元、6 000万元.得到分时段的公交专用道布局方案如表5和图2所示.在成本约束下，路网在3个时段内生成的公交专用道的建设规模分别为39.6、116.4和230.4 km，并产生36.2万元的消费者剩余价值.随着公交专用道投资规模的逐步扩大，产生的网络效益也逐步提高.

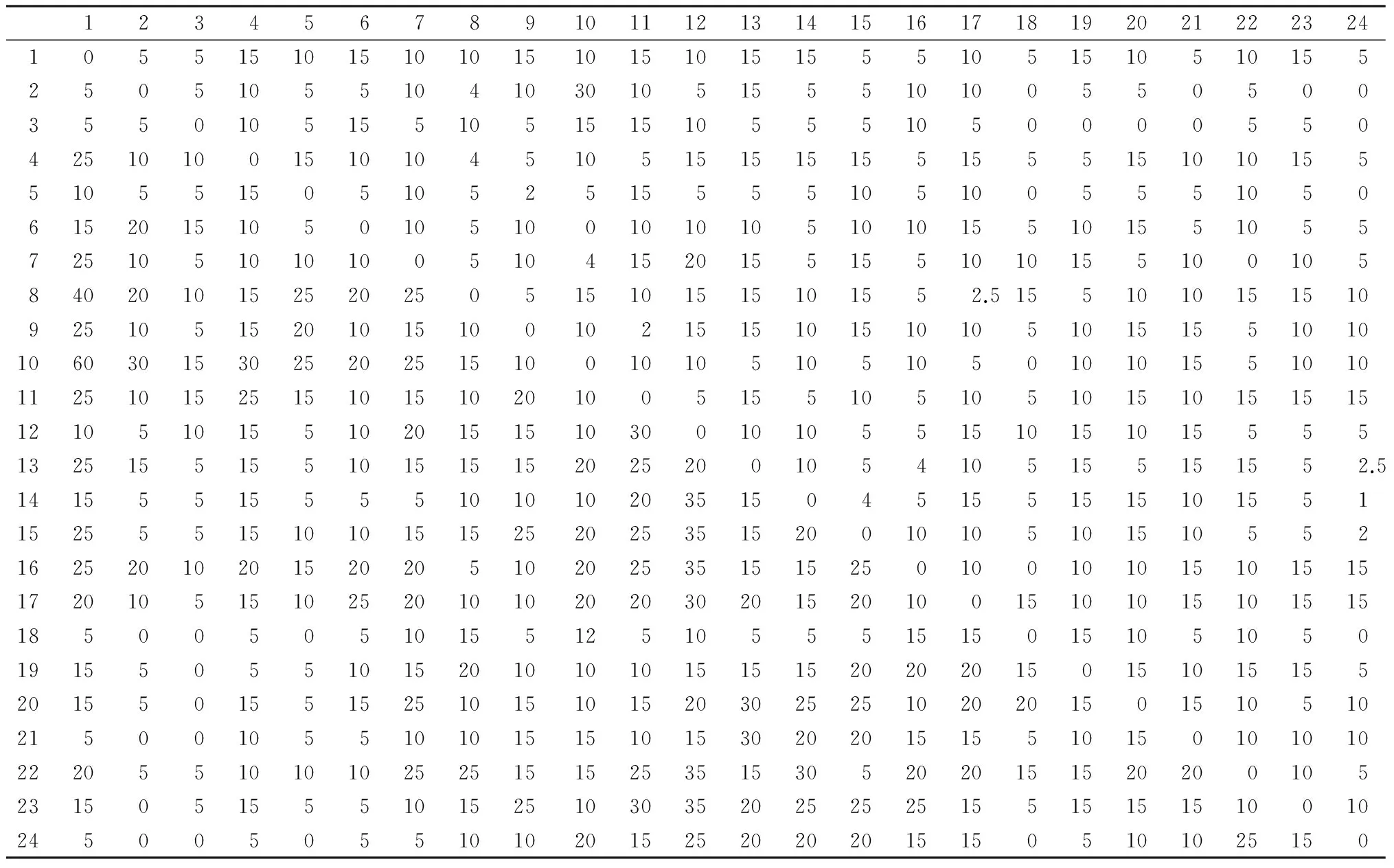
表4 OD需求分布

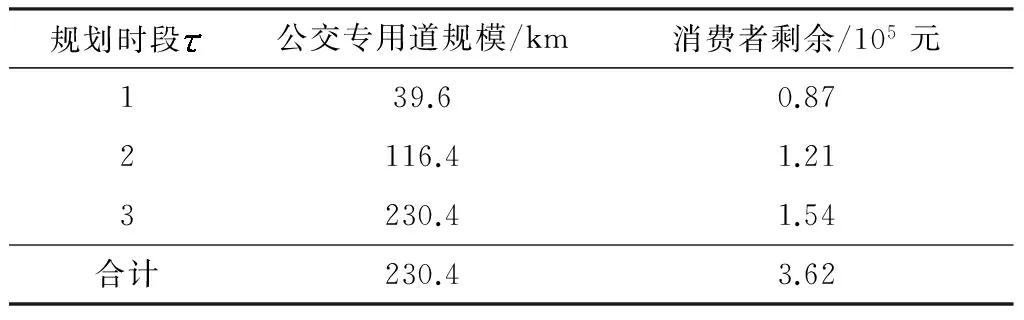
表5 分时段测试路网性能

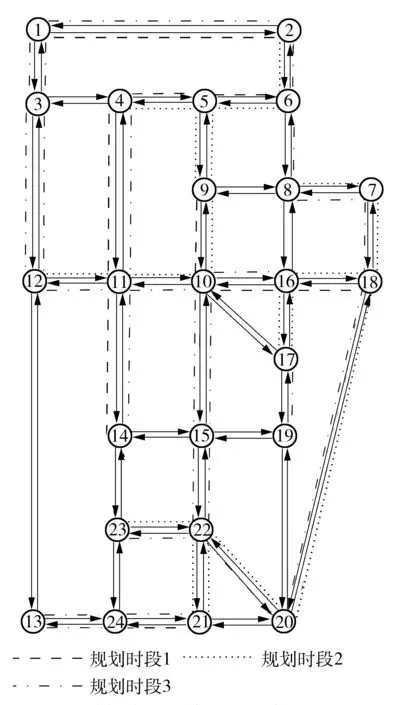
图2 公交专用道网络布局方案

表6 同步与连续优化策略计算结果

Table 6 Calculation results of simultaneous and sequential approaches

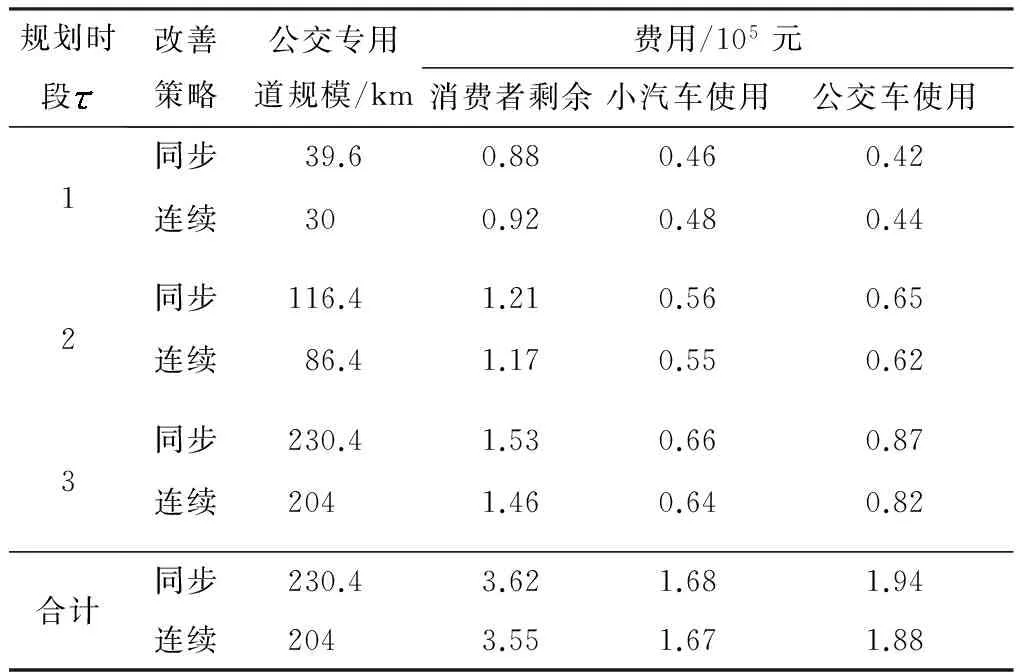
规划时段改善策略公交专用道规模/km费用/105元消费者剩余小汽车使用公交车使用123合计同步39.60.880.460.42连续300.920.480.44同步116.41.210.560.65连续86.41.170.550.62同步230.41.530.660.87连续2041.460.640.82同步230.43.621.681.94连续2043.551.671.88

方案比选过程如下.

为进一步揭示公交专用道与网络性能的关系，文中选取以网络的目标值等作为指标值，对比以下3种不同优化策略路网特性(结果如表7所示):

①分时段公交专用道最优布局方案(文中方案)；

②无公交专用道方案；

③全设公交专用道方案.

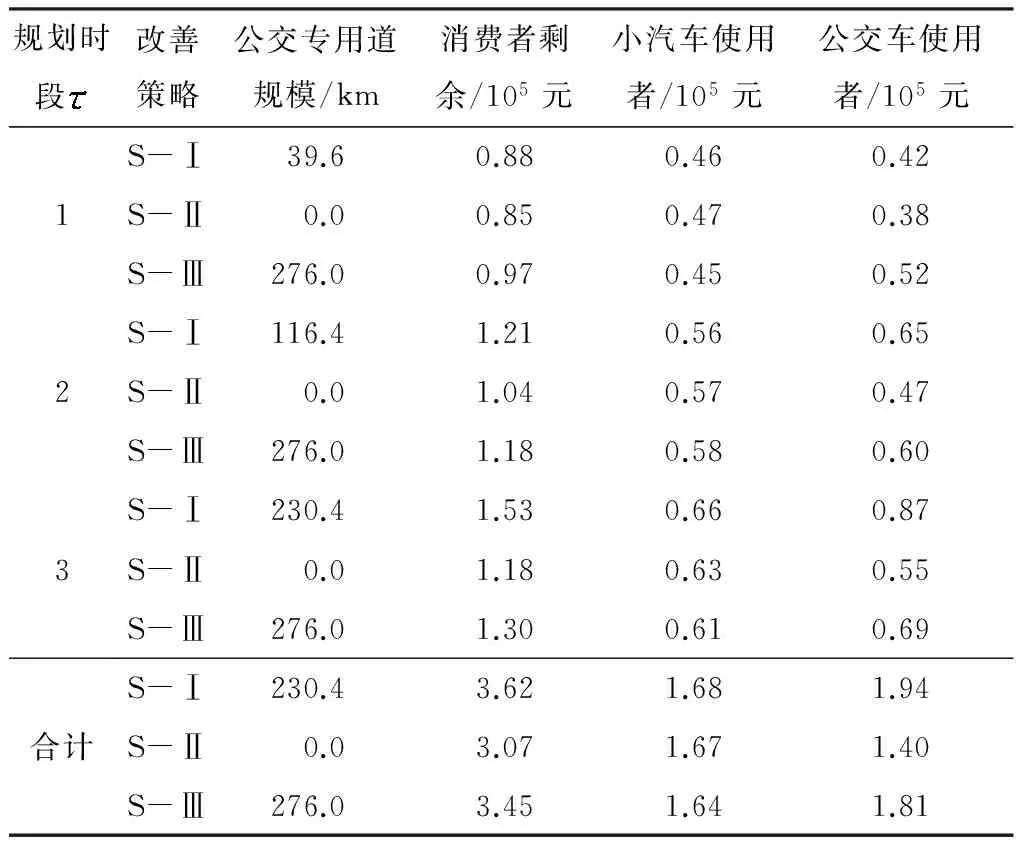
表7 不同情景模型计算结果

对比分析文中提出的组合优化模型与其他策略，可以看出：

与策略②、③下的网络特性指标对比发现，策略①(文中方案)的网络改善效果更优，可以产生更高的消费者剩余.进一步分析策略①下的网络特性变化特征，网络的消费者剩余价值基本上随着规划时段发展而呈现增长趋势.

在策略②下，由于路网中未设置公交专用道，在3个规划时段内，网络消费者剩余始终低于策略①；在策略③下，全路段设置公交专用道的布局方法显然不符合路网交通情况，虽然相比于策略①，策略①可以带来更高的公交车使用者的消费者剩余，但是明显降低了小汽车使用者的消费者剩余，导致整个路网整体效益降低，因此策略①的网络效益仍然优于策略③.

进一步分析公交专用道建设规模与投资约束之间的关系，设定投资系数N(投资矩阵倍数)为0.5、1.0、1.5以及无约束4种成本约束情景，结果如表8所示.随着N的增加，公交专用道规模以及消费者剩余呈增大趋势，且公交车使用者的剩余价值增加幅度相比于小汽车的逐渐增大.在无投资约束条件下，公交专用道的规模仍然低于全设公交专用道的建设规模.

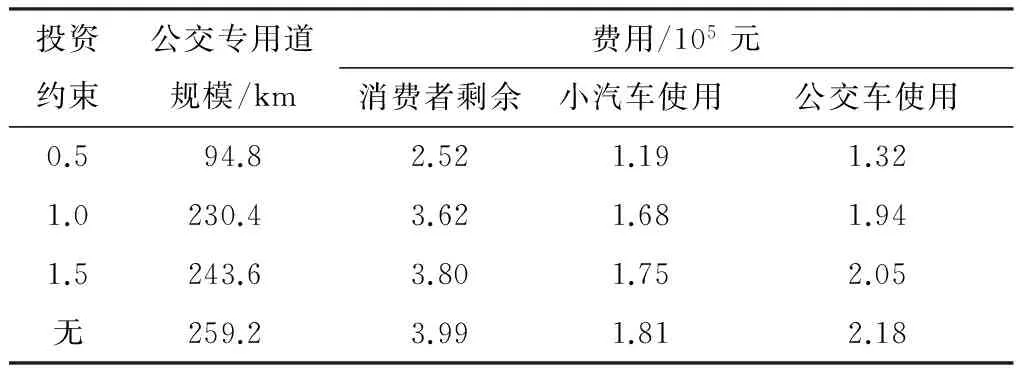
表8 不同投资成本情景的计算结果

综上所述，公交专用道的建设能够产生较好的消费者剩余价值，且公交车使用者的效益更为明显.同时，最优的公交专用道布局能够产生更好的网络性能.

5 结语

文中针对考虑“时间维”的公交专用道网络布局优化问题进行了研究.通过使用网络分析方法，建立了以最大化路网消费者剩余最大化为优化目标的双层规划模型，并进行了算例验证分析，同时给出了基于MSWA的GA算法.该优化模型能够贴切体现现实道路环境，客观反映公交专用道选址的实际特性与规划实践需求，同时，兼顾了交通需求动态变化对公交专用道布局方案的影响.文中验证了同步优化专用道布局方法相较于连续优化的优越性.

为了使该布局优化模型更能真实反映现实世界的城市交通改善需求，接下来，笔者将进一步对此模型进行深入优化，考虑基于交通走廊的连续公交专用道选址模型，研究“分时段”且“连续”的公交专用道布局方案.同时，考虑结合实际路网数据，对模型及求解算法的合理性和有效性进行科学验证，使文中研究成果兼具理论价值和实践意义.

[1] CURRIE G,SARVI M,YOUNG W.A comprehensive approach to balanced road space allocation in relation to transit priority [C]∥Proceedings of 83rd Transportation Research Board Annual Meeting.Washington D C:Transportation Research Board,2004:1-14.

[2] ZHU L,YU L,CHEN X M,et al.Simulated analysis of exclusive bus lanes on expressways:case study in Beijing [J].Journal of Public Transportation,2012,15(4):125.

[3] GAN A,YUE H,UBAKA I,et al.Development of operational performance and decision models for arterial bus lanes [J].Transportation Research Record:Journal of the Transportation Research Board,2003,1858(1):18-30.

[4] ARASAN V T,VEDAGIRI P.Bus priority on roads carrying heterogeneous traffic:a study using computer simulation [J].European Journal of Transport and Infrastructure Research,2008,8(1):45-64.

[5] SURPRENANT-Legault J,El-GENEIDY A M.Introduction of reserved bus lane [J].Transportation Research Record:Journal of the Transportation Research Board,2011,2218(1):10-18.

[6] LI S,JU Y.Evaluation of bus-exclusive lanes [J].IEEE Transactions on Intelligent Transportation Systems,2009,10(2):236-245.

[7] MESBAH M,SARVI M,CURRIE G.New methodology for optimizing transit priority at the network level [J].Transportation Research Record:Journal of the Transportation Research Board,2008,2089(1):93-100.

[8] MESBAH M,SARVI M,OUVEYSI I,et al.Optimization of transit priority in the transportation network using a decomposition methodology [J].Transportation Research Part C:Emerging Technologies,2011,19(2):363-373.

[9] MESBAH M,SARVI M,CURRIE G,et al.Policy-making tool for optimization of transit priority lanes in urban network [J].Transportation Research Record:Journal of the Transportation Research Board,2010,2197(1):54-62.

[10] MESBAH M,SARVI M,CURRIE G.Optimization of transit priority in the transportation network using a genetic algorithm [J].IEEE Transactions on Intelligent Transportation Systems,2011,12(3):908-919.

[11] YAO J,SHI F,ZHOU Z,et al.Combinatorial optimization of exclusive bus lanes and bus frequencies in multi-modal transportation network [J].Journal of Transportation Engineering,2012,138(12):1422-1429.

[12] MIANDOABCHI E,FARAHANI R Z,SZETO W Y.Bi-objective bimodal urban road network design using hybrid a new approach to evaluating on-road public transport priori-ty metaheuristics [J].Central European Journal of Operations Research,2012,20(4):583-621.

[13] LO H K.SZETO W Y.Time-dependent transport network design under cost-recovery [J].Transportation Research Part B:Methodological,2009,43(1):142-158.

[14] SZETO W Y,LO H K.Time-dependent transport network improvement and tolling strategies [J].Transportation Research Part A:Policy and Practice,2008,42(2):376-391.

[15] SZETO W Y,LO H K.Strategies for road network design over time:robustness under uncertainty [J].Transportmetrica,2005,1(1):47-63.

[16] SZETO W Y,JABER X,O’MAHONY M.Time-dependent discrete network design frameworks considering land use [J].Computer-Aided Civil and Infrastructure Engineering,2010,25(6):411-426.

[17] 孙强,王庆云,高咏玲.不确定需求条件下多阶段区域综合交通网络设计的双层规划模型 [J].交通运输系统工程与信息,2011,11(6):111-116. SUN Qiang,WANG Qing-yun,GAO Yong-ling.Multi-period bi-level programming model for regional comprehensive transport network design with uncertain demand [J].The Journal of Transportation Systems Engineering and Information Technology,2011,11(6):111-116.

[18] LONG J,GAO Z,ZHANG H.et al.A turning restriction design problem in urban road networks [J].European Journal of Operational Research,2010,206(3):569-578.

[19] LIU H X,HE X Z,HE B S.Method of successive weighted averages(MSWA)and selfregulated averaging schemes for solving stochastic user equilibrium problem [J].Networks & Spatial Economics,2009,9(4):485-503.

[20] LEBLANC L J,MORLOK E K,PIERSKALLA W P.An efficient approach to solving the road network equilibrium traffic assignment problem [J].Transportation Research,1975,9(5):309-318.

Optimization Model to Locate Exclusive Urban Bus Lanes Considering Time Dimensionality

LUXiao-lin1PANShu-liang2ZOUNan1

(1.School of Control Science and Engineering, Shandong University, Jinan 250061, Shandong, China;2.Jinan Quantong Information Technology Co., Ltd., Jinan 250101, Shandong, China)

Aiming at the location and construction sequence approach of exclusive urban bus lanes in a certain planning period, this paper analyzes the location and construction practice as well as the dynamic change of realistic demands, and establishes a time-dependent bi-level optimization model to locate exclusive bus lanes. The upper level of the proposed model is a locating model to maximize the total consumer surplus in the whole road network, and the lower level is an allocation model of cars and buses to minimize the generalized travel cost. Then, with the help of genetic algorithm, the mentioned problem is solved. Moreover, a case study is performed to verify the effectiveness and practicability of the established bi-level model and to reveal the superiority of the proposed approach considering time dimensionality to the simply-phased sequential approach. The results show that the established model can simultaneously optimize the location and construction sequence of exclusive bus lanes.

public transit; exclusive bus lane; time dimensionality; bi-level programming model; genetic algorithm

2016-01-29

国家科技支撑计划项目(2014BAG03B04) Foundation item: Supported by the National Key Technology Research and Development Program(2014BAG03B04)

卢小林(1988-)，女，博士生，主要从事城市交通规划与设计研究.E-mail:luxiaolin1314@gmail.com

† 通信作者: 邹难(1976-)，男，教授，博士生导师，主要从事城市交通设计与智能控制研究.E-mail:nanzou@sdu.edu.cn

1000-565X(2017)04-0124-08

U 492.1+1

10.3969/j.issn.1000-565X.2017.04.018