电连接器接触件的插拔和温升特性*

贺占蜀 张远西 王培卓 汤勇 邵丽娜

(1.郑州大学 机械工程学院∥抗疲劳制造技术河南省工程实验室， 河南 郑州 450001;2.华南理工大学 表面功能结构先进制造广东普通高校重点实验室， 广东 广州 510640)

电连接器接触件的插拔和温升特性*

贺占蜀1张远西1王培卓1汤勇2邵丽娜1

(1.郑州大学 机械工程学院∥抗疲劳制造技术河南省工程实验室， 河南 郑州 450001;2.华南理工大学 表面功能结构先进制造广东普通高校重点实验室， 广东 广州 510640)

电连接器接触压力过大或过小都将导致不易插拔或接触电阻过大,最终导致接触失效.为了提高电连接器的接触可靠性,对一种电连接器接触件的插拔特性和温升特性进行了研究.采用ABAQUS软件对接触件进行了插拔力与温升仿真,研究了接触件结构参数弹舌倾角α和弹舌支撑间隙δ对插拔力的影响以及导线截面积S和电流对温升的影响,并通过实验研究了插拔力和温升的变化情况.结果表明:当δ=0.12 mm时,插拔力随α的增大而增大；当δ=0.18 mm时,插拔力随α增大先增大后减小;α一定时,插拔力随δ增大而逐渐较小；接触件温升随电流的增大而增大,随导线截面积增大而减小.实验得到的插拔力和温升结果与仿真结果吻合.综合考虑插拔与温升,产品最优参数为间隙弹舌支撑δ=0.12 mm、弹舌倾角α=15°.

电连接器；接触电阻；插拔力；温升；有限元仿真

电连接器是一种用于实现信号与电流传输和控制的电接触元件[1],其内部接触件的接触失效是电连接器的主要失效模式,大约占失效总数的45.1%[2-3],失效的原因主要有两个方面:①接触压力过大,插拔力随之增大,将导致连接件不易插拔；②接触压力过小,导致插拔力不足,接触件容易松脱,同时将导致接触电阻过大,最终引起温升过高.因此,为了提高电连接器的接触可靠性,有必要对电连接器接触件的插拔特性和温升特性进行分析研究.

国内外学者先后采用仿真和实验方法对电连接器、断路器、继电器等电接触元件进行了研究.Do等[4]建立了一种高速差分电连接器的多场耦合模型,对不同触点材料的电连接器的温度场进行了仿真,并通过实验对仿真结果进行验证.Angadi等[5]建立了一种汽车电连接器的机电热多场耦合模型,对接触压力、通电电流和环境因素综合作用下的温度场进行了仿真,模型中还考虑了粗糙表面对接触电阻的影响.Carvou等[6]通过ANSYS软件仿真了一种电连接器接触件插拔时的应力场和通电时的温度场,插拔力大小和温度变化都与实验相一致.Beloufa[7]采用仿真与实验相结合的方法，研究了接触面粗糙度对汽车用铜合金电连接器接触件的接触电阻的影响.

国内刘帼巾等[8]对接触器式继电器发生接触不良的失效机理进行了研究，发现接触器式继电器的主要失效模式是触点间接触不良，触点间过大且不稳定地接触电阻.潘骏等[9]针对电连接器接触件进行结构力学与接触情况研究,利用ANSYS软件对接触件的接触情况进行运动仿真,得到了接触过程中接触压力、插拔力的变化情况和应力分布情况.任万滨等[10-11]采用ANSYS软件仿真了密封电磁继电器在高、低温环境条件下的温度场,结果表明触点的电流密度是影响稳态温升的关键因素;不仅如此,还仿真了电连接器接触件的插拔力,分析了摩擦系数、过盈量等因素对插拔特性的影响,并建立电热耦合模型对接触电阻进行仿真分析.周泽广等[12]采用热网络分析法研究了温差发电器冷端在空气自然对流、强制对流以及水冷等3种不同散热条件下的传热特性，并进行了实验研究.Wang等[13]基于涡流场、气流场和温度场,多场耦合模拟了自然对流和强迫对流条件下的整个开关柜温升分布,并对弹簧接触结构、真空断路器和电流互感器进行了优化以减小温升.

虽然国内外对电连接器的研究取得了一定成果,但针对接触件结构参数对插拔特性的影响研究较少.为了提高电连接器接触可靠性,文中针对一种电连接器接触件的插拔特性和温升特性进行深入研究,采用ABAQUS软件对接触件进行了插拔与温升仿真,研究了接触件结构参数弹舌倾角α和弹舌支撑间隙δ对插拔力的影响以及导线截面积S和电流对温升的影响,并通过试验研究了插拔力和温升的变化情况.

1 理论分析

1.1 接触件插拔特性

电连接器中的接触件都是成对出现的,图1为一种电连接器接触件,包括插头端子和插座端子.当插头端子插入插座端子时,因受到弹力的作用,接触件间产生接触压力,这将直接成为插拔时的阻力.根据胡克定律,当弹性接触件的弹力越大,也就是接触件间的接触压力越大时,为克服此力产生的阻力而所需的力也越大,也就是插拔力越大;反之亦然.在插入与拔出过程中,如图1(a)所示,接触件受到的插拔力、接触压力、摩擦力保持稳定:

(1)

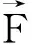
摩擦力主要取决于两个接触件之间的摩擦系数,对于需要多次插拔的电连接器来说,接触件表面的磨损将导致摩擦系数变化.而接触压力是影响插拔力的主要因素,它不但与接触件材料的性能有关,还与接触件内部结构参数有关,如图1(b)中的弹舌倾角α和弹舌支撑间隙δ.

1.2 接触压力与接触电阻

接触压力不仅影响插拔力,在它的作用下接触件相互得以接触,电流接通,接触电阻也随之产生[13],而接触电阻与接触件的生热率直接相关.随着接触压力的增大,接触件上用于传输电流的真实电接触面(非表观面积)也将增大,那么接触电阻也将随之减小.经验公式为

R=K(0.102P)m

(2)

式中，R为接触电阻，P为接触力，K为与接触材料性质和接触表面情况有关的系数，m为与接触形式、压力、范围和实际接触面的数目有关的指数(实验证明,在接触压力不太大的范围内,对于点接触,m=0.5;对于线接触,m=0.7;对于面接触,m=1).为了减小接触电阻,要求接触压力尽可能大，但过大的接触压力也将导致插拔力过大而不易插拔，而且接触压力大到一定程度,接触电阻减小幅度变小,此时再通过增大接触压力来减小接触电阻反而得不偿失.因此，设计接触件时要选择合适的接触压力,既保证较小的插拔力又保证温升不至过大.

1.3 接触件温升特性

电连接器的温升计算时,需要考虑电连接器接触件的生热率以及传导、对流和辐射3种传热方式引起的热量散失.

图2 接触件散热示意图

电连接器接触件的生热率是指在电连接器的接触件上施加额定的电流时,接触件在单位时间内释放的热量.除了接触件之间的接触电阻R1,电连接器还有接触件自身的体积电阻R2、接触件与导线之间的压接电阻R3和导线自身的体积电阻R4.考虑到金属材料的电阻率随温度变化,引入电阻温度系数a,则单个接触件的生热率为

q=I2(R1+R2+R3+R4)[1+a(Tc-20)]

(3)

式中:I为通过导体的电流;Tc为元器件自身湿度.本实验中,R1=0.32 mΩ，R2=1.46 mΩ，R3=0.29 mΩ,导线电阻R4随导线长度变化,输入电阻率由仿真模型自行计算.

接触件在通电后发出的热量一部分通过导线传导出去,一部分通过热对流与热辐射散发到空气中,最终达到热平衡.因此,在进行电连接器的温升计算时,需要考虑热传导、热对流和热辐射3种传热方式引起的热量散失.

热传导在电连接器里是一种重要的传热方式,热量经过导线然后通过导线绝缘皮向外传导.由傅里叶定律可得

(4)

电连接器的热对流方式主要是电连接器的外表面与周围空气之间的自然对流,在进行计算时,对流换热系数按照空气自然对流换热系数来取值.热对流可以使用牛顿冷却方程来描述:

Φ=hA2Δt

(5)

式中:A2为与流体接触的壁面面积;Δt为物体与流体表面间的温差;h为为对流换热系数,针对接触件,采用大空间自然对流换热系数.

物体表面的温度越高,热辐射效应就越明显.物体表面的辐射遵循Stefan-Boltzmann定律:

q=εσA(T4s-T4b)

(6)

式中:ε为发射率,接触件为轻微氧化镀锡黄铜,发射率取0.2;σ为Stefan-Boltzmann常数,约为5.67×10-8W/(m2·K4);Ts为发热体表面的绝对温度,K;Tb为外界环境绝对温度,K.工程中,常把辐射换热折算成对流换热处理.结合式(5),可以推出辐射换热系数:

(7)

本实验的环境温度为25 ℃，仿真所采用的大空间自然对流换热系数和折算后的辐射换热系数如表1所示.

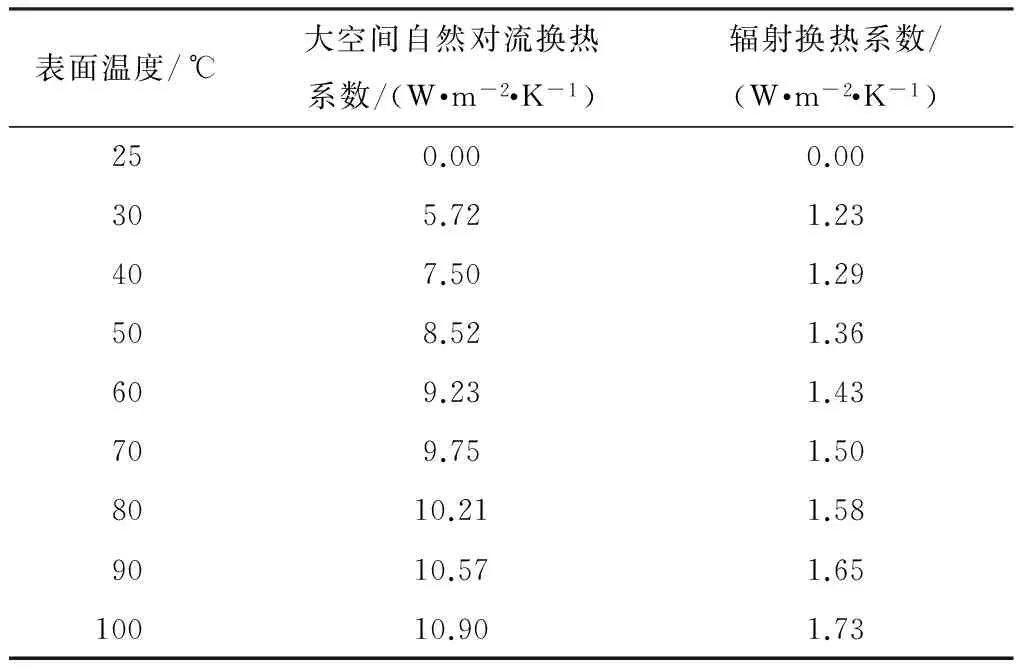
表1 接触件换热系数

2 仿真与实验

2.1 插拔的仿真与实验设置

在Solid Works2014中建立电连接器接触件模型,然后导入到ABAQUS6.12软件，采用通用静态分析步进行有限元仿真.在Property模块中定义各零件的材料属性,插头端子与插座端子材料均为H65,其力学性能为:弹性模量105 GPa，泊松比0.35，屈服强度420 MPa.为保证ABAQUS/Standard 求解收敛,将插拔过程分成3个分析步:Incompact、In和Out,即预接触分析步、插入分析步和拔出分析步.在Interaction模块中定义各零件的接触情况,插头端子和插座端子之间接触模型中使用有限滑移,定义库伦摩擦,摩擦系数为0.2.在Load模块中初始分析步中设置插座端子上下底部采用完全固定约束.在插头端子参考点上设置位移载荷,插入分析步位移量为3.5 mm,拔出分析步位移量则为0,即返回初始位置.插头端子与插座端子均采用C3D10M网格,即修正的二次四面体单元,图3为划分网格后的接触件.

图3 接触件网格划分

为了验证仿真分析的正确性,对电连接器进行插拔实验,测量插入力和拔出力.在插拔实验之前,采用深圳洁盟清洗设备有限公司生产的JP-020S超声波清洗机对接触件清洗10 min,以去除油污和其他杂质.然后采用深圳三思纵横科技股份有限公司生产的连接器插拔力专用试验机(UTM2103)进行插拔实验(图4),试验机下方的力传感器将采集的力信号转变为电信号传输到计算机.

图4 插拔力实验机

2.2 温升的仿真与实验设置

在插拔仿真之后,将插入状态下变形后的网格信息提取出来,替换原有文件中的初始网格信息,并重新生成、导入该文件,进行温升仿真.电连接器两端的连接导线实际由多根细铜丝组成,仿真时为了简化模型,把导线所有细铜丝等效为单根相同截面积的三维圆柱体导线模型,导线对流传热可以表示为

Φ=hcA3Δt=heqA3eqΔt

(8)

式中:hc为导线对流换热系数;A3为导线所有铜丝的总换热面积，该数值可几何计算得出;Δt为物体与环境温度之间的温差，该数值通过热电偶测量得出;heq为等效的单根导线对流换热系数,该数值通过实验和计算相结合的方法得出;A3eq为等效的单根导线换热面积，该数值也可几何计算得出;实验采用了3种不同截面积的导线,分别为0.85,1.00和1.25 mm2,对应的等效对流换热系数分别为60.0、51.5和50.5 W/(m2·K).

材料的热学和电学特性如表2所示.接触件接触部位、接触件与导线接触部位的接触属性都选择为Tie.分析步模块中定义测量分析步并选择热电耦合计算方式.设置接触电传导系数Ecc:

(9)

式中，R1为接触电阻，Ac为电接触面积.设置接触热传导系数Tcc如下:

(10)

式中，k为电阻率，ρ为热导率.将热辐射折算成辐射换热系数,与自然对流换热系数一并输入.最后加载面电流载荷,得到温度分布云图.

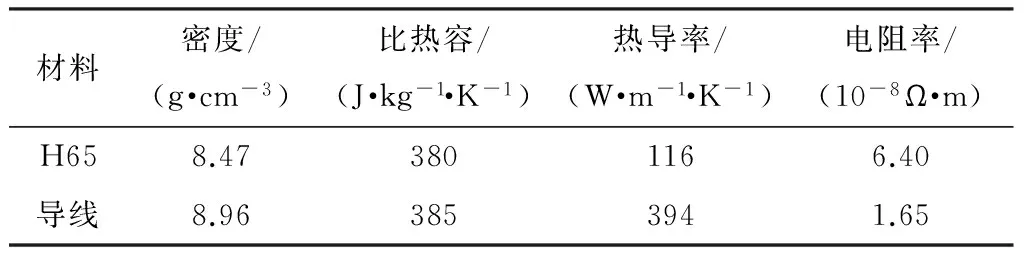
表2 接触件和导线热力学特性

本实验采用热电偶法进行测量.温升实验仍然采用清洗过的接触件,将多对相同接触件通过不同粗细的导线压接并串联起来.实验采用图5所示WYK-50A直流稳压电源,通入不同大小的恒定电流,将K形热电偶粘到每个插座端子表面测量温度,再通过8422-51多通道数据记录仪将采集的温度信号转变为电信号,传输到计算机.

图5 温升实验装置

3 结果分析

3.1 插拔的仿真与实验结果

插拔时,插座端子的两个结构参数弹舌倾角α和弹舌支撑间隙δ直接决定着接触压力和插拔力的大小.为了确定最优参数,在仿真时调整α和δ的大小,分析接触压力和插拔力的变化.

插头端子插入插座端子后,插座端子弹舌最高点下降的高度设置为0.15 mm.当间隙δ小于0.15 mm时,如图6(a)所示,δ=0.12 mm,α从9°增大到42°,接触压力、插入力和拔出力分别从11.2、4.7和4.4 N增大到35.5、19.7和7.8 N;当间隙δ大于0.15 mm时,如图6(b)所示,δ=0.18 mm,接触压力、插入力和拔出力随α从9°增大到42°而先增大后减小,在α=24°时达到最大值,分别为13.0、6.6和3.7 N.这是因为在其他条件不变的情况下,接触压力和插拔力的大小主要由插入时弹舌支撑脚与水平面的夹角α′和弹舌支撑脚产生的挠度决定.而不论间隙为何值,α增大会使α′增大,同时弹舌支撑脚长度减小,将导致插入后的弹舌支撑脚挠度减小.在两者共同作用下,接触压力和插拔力随α增大先增大后减小.而δ增大使弹舌支撑脚挠度减小量增大,从而使接触压力达到最大值的角度α减小.所以当δ=0.12 mm、α在9°～42°时，接触压力和插拔力尚未到达最大值,所以随α增大持续增大;而当δ=0.18 mm时,接触压力和插拔力在α=24°时达到最大值,因此随α从9°增大到42°而先增大后减小.

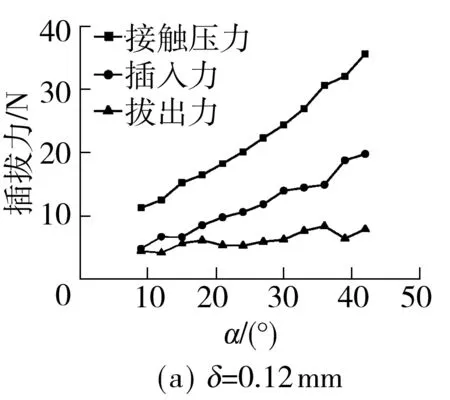
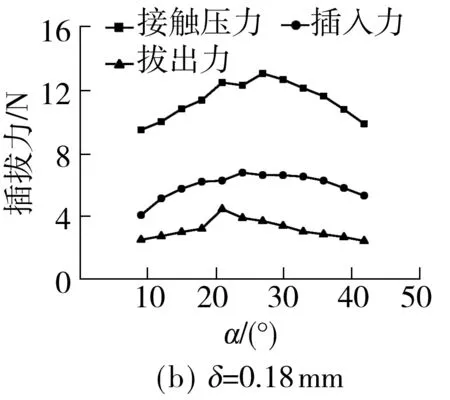
图6 角度α对接触压力和插拔力的影响Fig.6 Effects of α on contact force and insertion-extraction force

如图7所示，α=15°时,随着δ从0增大到0.3 mm,接触压力、插入力和拔出力分别从15.7、8.8和4.0 N逐渐减小至2.6、1.0和1.0 N,δ从0.3 mm增大至0.4 mm,接触压力和插拔力保持不变.这是因为,当δ小于0.1 mm时,插座端子发生塑性变形,即便间隙再减小,接触压力也不再增大;当δ在0.1～0.3 mm时,随着间隙增大,接触压力减小;当δ大于0.3 mm时,即便角度再增大,尾部也不再支撑起作用,插拔接触压力不再变化.所以δ应在0.1～0.3 mm之间.

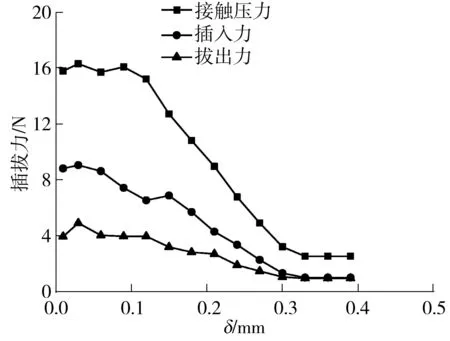
图7 间隙δ对接触压力和插拔力的影响

为了减小接触电阻,接触压力要足够大,但随着接触压力增大,插拔力也相应增大,对弹性接触件的性能要求也越高,接触件的磨损也增大.所以从使用者的角度考虑,接触压力不宜过大.综合考虑接触压力对插拔力和接触电阻的影响,最优参数为δ=0.12 mm、α=15°.图8为δ=0.12 mm、α=15°接触件插入时插座端子的应力分布云图.可以看出插座端子的最大应力出现在弹舌最高点和折弯处,但均未超过材料的屈服强度,接触件未发生塑性变形.

图8 应力分布云图

插拔力的仿真和实验结果对比如图9所示.以插头端子与插座端子开始接触点为位移零点,插入力为正,拔出力为负.随着插头端子的逐渐插入,弹舌挠度不断增加,插入力逐渐增大,在插头端子到达弹舌最高点时达到最大值.此时仿真最大插入力为6.86 N,略小于实验最大插入力7.22 N.随着插头端子继续插入,进入平稳插入阶段,接触压力方向由垂直于弹舌表面变成垂直于插头端子表面,所以在平稳插入阶段插入力减小并趋于稳定.在拔出阶段,拔出力由稳定状态逐渐减小,仿真最大拔出力为6.02 N,与实验最大拔出力6.09 N吻合.在拔出阶段,插头端子经过弹舌最高点后,接触压力方向又变成垂直于弹舌表面,有助于插头端子拔出,拔出力骤然减小.在最后拔出阶段，随着弹舌的挠度逐渐减小，插头端子受到的拔出力逐渐减小到零.仿真结果与实验结果吻合.

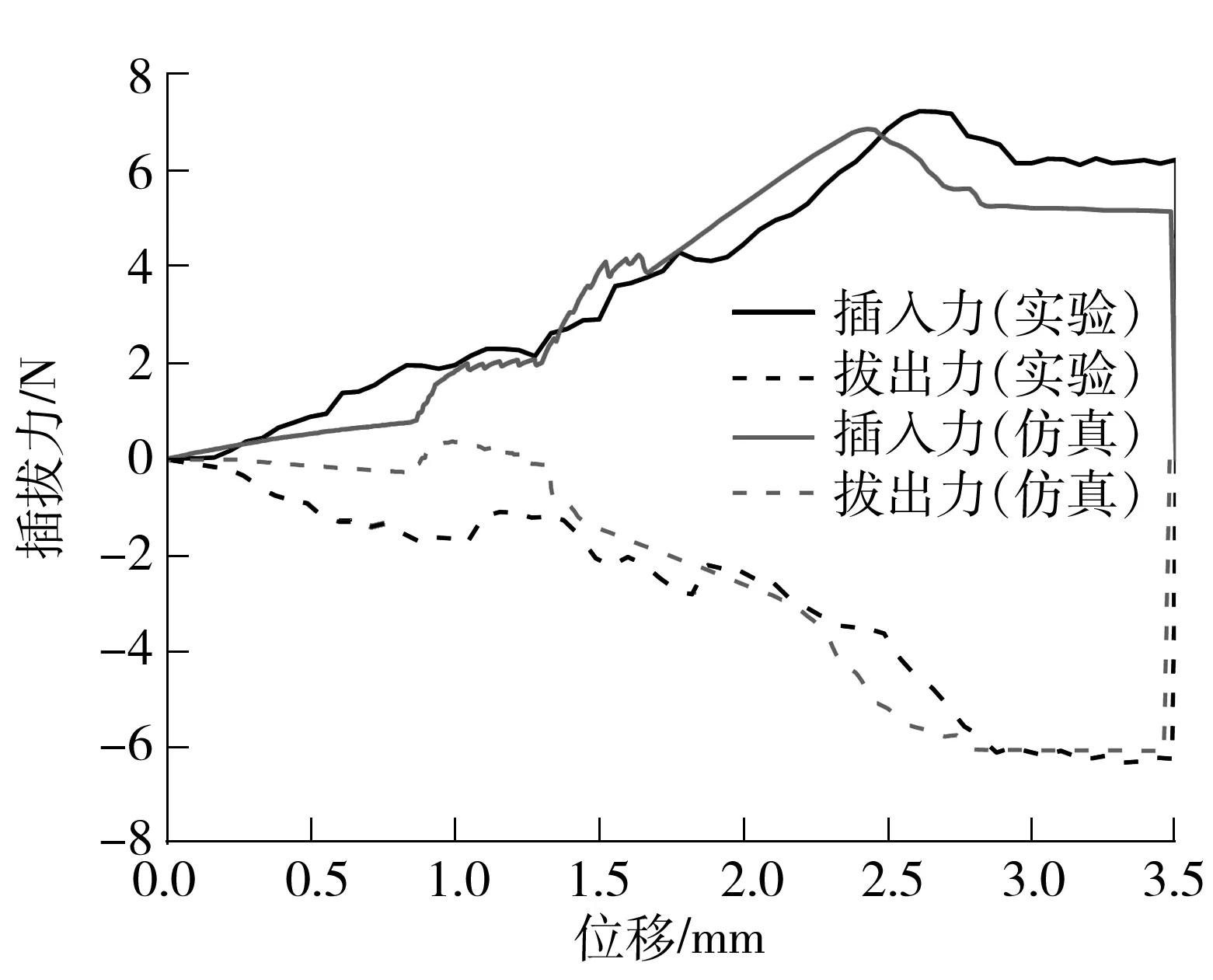
图9 插拔力实验结果与仿真结果对比

Fig.9 Contrast of insertion-extraction forces obtained from experiment and simulation

3.2 温升的仿真与实验结果

电连接器工作时,通入的电流大小会对温升产生影响,因此仿真分析了不同电流(5,8,11,14,17,20 A)下的温升,图10为施加20 A电流条件下,稳定后的温度分布云图.可以看出,接触件最高温度产生在两端子接触区,最大温升为72.3 ℃,插头和弹舌部位温升最高;因散热表面积相对较大,插座端子最高温度小于插头端子.

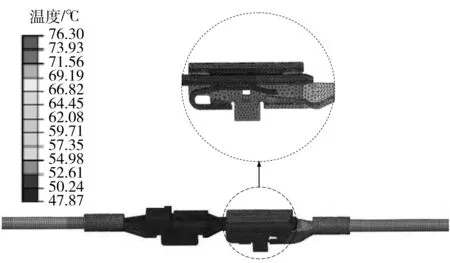
图10 温度分布云图

为了评估接触电阻和辐射散热对电连接器温升的影响,对不考虑接触电阻和辐射散热的情况进行了温升仿真.图11为导线截面积为0.85 mm2时接触电阻和辐射散热对最大温升的影响.在加载不同电流的情况下,去除接触电阻，接触件最大温升下降11%,由此可知接触电阻对最大温升影响明显;而在不考虑辐射散热的情况下,接触件最大温升增大了4%,辐射散热效应相对较小.

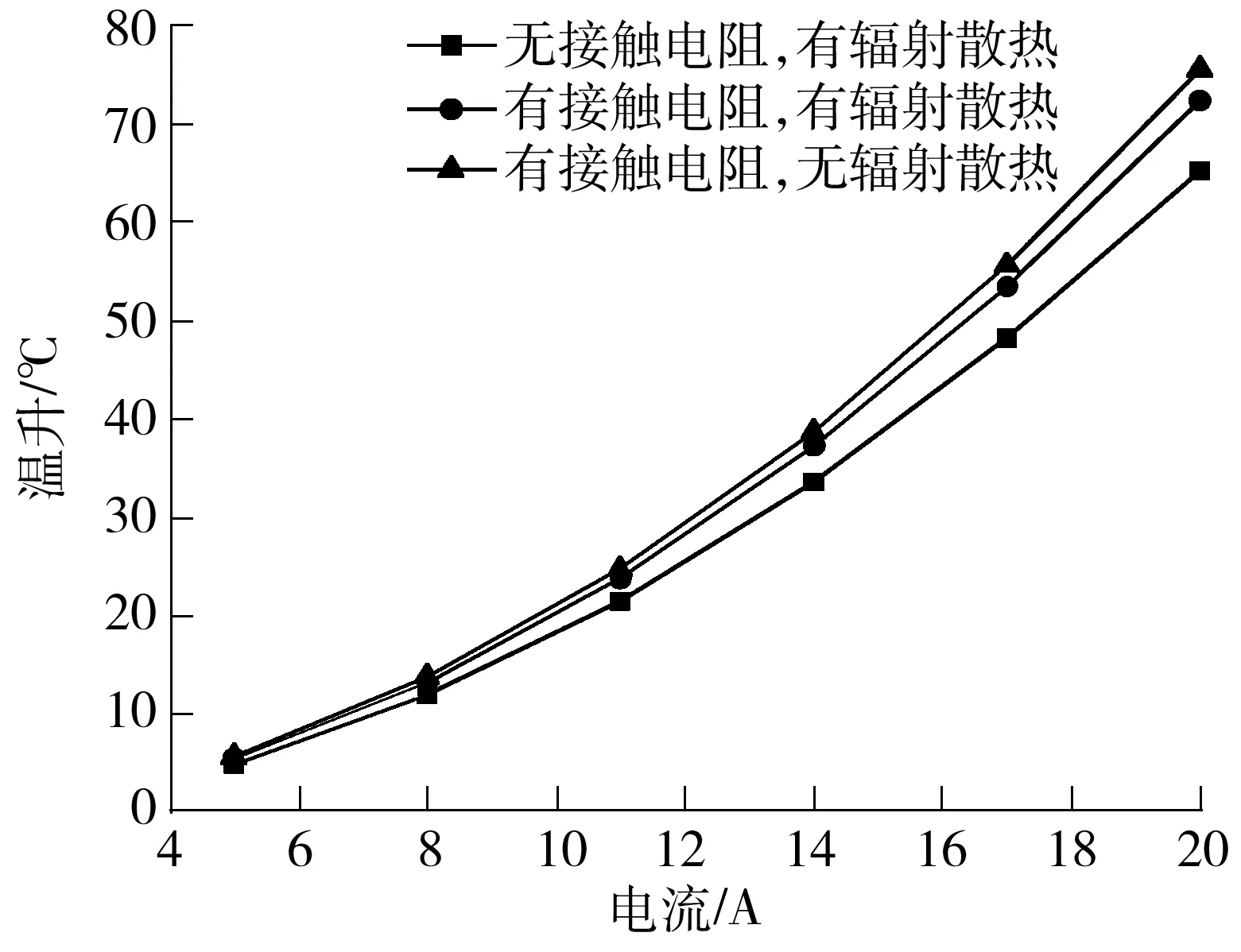
图11 接触电阻和辐射散热对温升的影响

Fig.11 Effects of contact resistance and heat radiation on temperature rise

图12所示为施加14 A恒定电流时仿真和实验得到的接触件温升瞬态曲线.可以看到仿真结果和实验结果趋势一致,温度在150 s内迅速升高达到稳定状态,且温升趋势符合热量指数增长规律[15]:

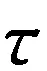
(11)

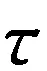
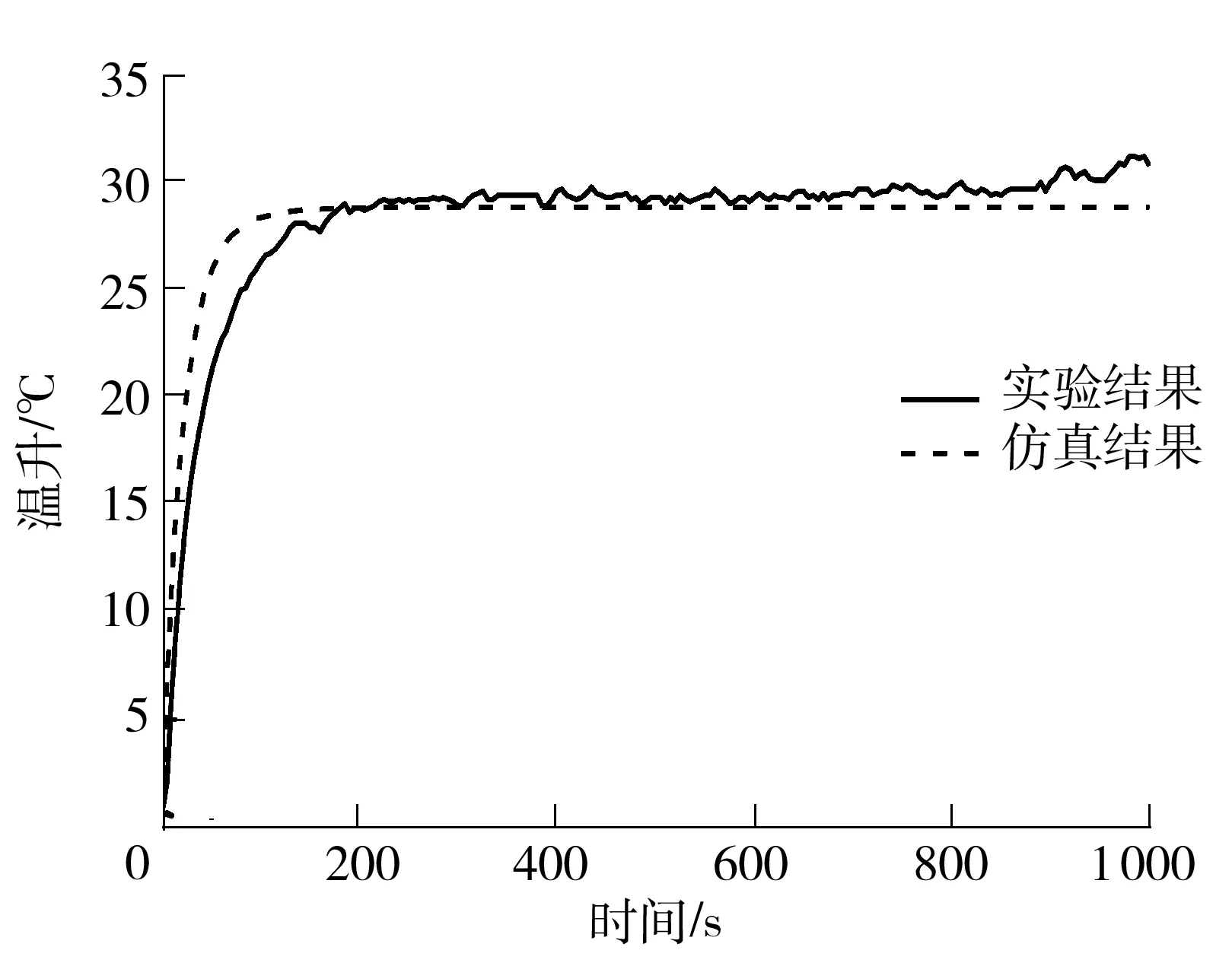
图12 温升实验结果与仿真结果对比

Fig.12 Contrast of temperature obtained from experiment and simulation

在进行温升实验时,连接导线的规格也会对结果产生影响,导线截面积S对接触件温升的影响如图13所示.在相同的导线截面积下,接触件最大温升均随电流的增大而逐渐增大,这是因为电流的增大导致产生的热量增加.而在电流一定时,接触件最大温升随导线截面积增大而减小.这是因为连接导线较粗时,一方面自身电阻降低,另一方面传热能力增强，同时会额外起到散热的作用.在20 A电流时,S从0.85 mm2增加到1.0 mm2,增加了17%,最大温升从78 ℃下降到65 ℃,下降了20%;S再增加到1.25 mm2,增加25%,最大温升下降到59 ℃,只下降10%.这说明为了降低温升,可以适当增大导线直径,但导线截面积增大到一定程度后,温升下降幅度减缓,此时再通过增大直径来降低温升反而得不偿失.

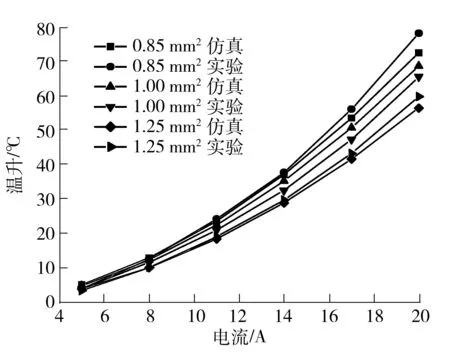
图13 导线截面积和电流对温升的影响

Fig.13 Effects of wire cross-section area and current on temperature rise

4 结论

文中通过ABAQUS有限元分析软件,对电连接器接触件进行了插拔和温升仿真，并进行了插拔力和温升实验,得到以下结论:

1)当δ=0.12 mm时,插拔力和接触压力随α的增大而增大;当δ=0.18 mm时,插拔力和接触压力随α增大而先增大后减小；而当α=15°时,插拔力和接触压力随弹舌支撑间隙δ增大而逐渐减小.

2)温升分析表明,在相同的导线截面积下,接触件最大温升均随电流的增大而逐渐增大;而在输入电流一定时,接触件最大温升均随导线截面积增大而减小.

3)实验得到的插拔力和温升结果与仿真结果吻合,验证了仿真分析的准确性.综合考虑插拔与温升,本实验中产品最优参数为δ=0.12 mm、α=15°.

[1] 任万斌,王鹏,马晓明,等.微动诱发的触点电接触间歇失效现象研究 [J].摩擦学学报,2013,33(4):382-387. REN Wan-bin,WANG Peng,MA Xiao-ming,et al.Intermittency phenomenon of electrical contacts induced by fretting behavior [J].Tribology,2013,33(4):382-387.

[2] ITO T,OGIHARA S,HATTORIY Y.Observation of structural transition of tin plated fretting contacts using FIB-SEM [J].IEICE Transactions on Electronics,2011(9):1350-1355.

[3] ITO T,NOMURA Y,HATTORIY Y.Observation of tin plated fretting contacts using FIB-SEM [J].IEICE Transactions on Electronics,2010(9):1452-1455.

[4] DO T K,COHEN T.Coupled thermal electrical finite element analysis of power contacts used in high speed diffe-rential connectors [C]∥Proceedings of the 55th IEEE Holm Conference on Electrical Contacts.Canada:[s.n.],2009:124-128.

[5] ANGADI S V,JACKSON R L,CHOE S,et al.A multi-physics finite element model of a 35A automotive connector including multiscale rough surface contact [C]∥Proceedings of the 56th IEEE Holm Conference on Electrical Contacts.Charleston:[s.n.],2010:392-402.

[6] CARVOU E,ABDI R E,RAZAFIARIVELO J,et al.Thermo-mechanical study of a power connector [J].Measurement,2012,45(5):889-896.

[7] BELOUFA A.Numerical and experimental optimization of mechanical stress,contact temperature and electrical contact resistance of power automotive connector [J].International Journal of Mechanics,2010,4(4):94-104.

[8] 刘帼巾,陆俭国,王海涛,等.接触器式继电器的失效分析 [J].电工技术学报,2011,269(1):81-85. LIU Guo-jin,LU Jian-guo,WANG Hai-tao.Failure analysis of contactor relay [J].Transactions of China Electro-technical Society,2011,269(1):81-85

[9] 潘骏,靳方建,陈文华,等.电连接器接触件结构分析与插拔试验 [J].中国机械工程,2013,22(12):1636-1641. PAN Jun,JIN Fang-jian,CHEN Wen-hua,et al.Structural analysis of electrical connector contacts and insertion-extraction test [J].China Mechanical Engineering,2013,22(12):1636-1641.

[10] REN W B,LIANG H M,ZHAI G F.Thermal analysis of hermetically sealed electromagnetic relay in high and low temperature condition [C]∥Proceedings of the 52nd IEEE Holm Conference on Electrical Contacts.Canada:[s.n.],2006:110-116.

[11] 任万滨,崔黎,翟国富,等.电连接器接触件插拔特性与接触电阻的仿真分析 [J].机电元件,2012,32(3):40-44. REN Wan-bin,CUI Li,ZHAI GUO-fu,et al.Simulation of contacts inserted characteristics and contact resistance for electrical connector [J].Electromechanical Components,2012,32(3):40-44.

[12] 周泽广,朱冬生,吴红霞,等.温差发电器的传热特性分析与实验研究 [J].华南理工大学学报(自然科学版),2011,39(11):47-52. ZE Guang,ZHU Dong-sheng,WU Hong-xia,et al.Heat transfer characteristic analysis and experimental investigation of thermoelectric generator [J].Journal of South China University of Technology(Natural Science Edition),2011,39(11):47-52.

[13] WANG Li-jun,ZHENG Wen-song,WANG Liu-huo,et al.Electromagnetic-thermal-flow field coupling simulation of 12kV medium voltage switchgear [J].IEEE Transactions on Components,Packaging and Manufacturing Technology,2016,6(8):1208-1220.

[14] 王召斌,翟国富,黄晓毅.电磁继电器贮存期接触电阻增长的动力学模型 [J].电工技术学报,2014,27(5):205-211. WANG Zhao-bin,ZHAI Guo-fu,HUANG Xiao-yi.Kine-tic model of contact resistance increment of electromagnetic relay in storage [J].Transactions of China Electrotechnical Society,2014,27(5):205-211.

[15] ZHU Z Y,LEE H P,CHEOK B T.Finite element analysis of thermal shock tests of RF connectors [J].Journal of Materials Processing Technology,2005,168:291-295.

Insertion-Extraction and Temperature Rise Properties of Electrical Connector

HEZhan-shu1ZHANGYuan-xi1WANGPei-zhuo1TANGYong2SHAOLi-na1

(1.School of Mechanical Engineering∥Engineering Laboratory of Anti-Fatigue Manufacturing Technology of Henan Province, Zhengzhou University, Zhengzhou 450001, Henan, China; 2.Key Laboratory of Surface Functional Structure Manufacturing of Guangzhou Higher Education Institutes, South China University of Technology, Guangzhou 510640, Guangdong, China)

Excessive or inadequate contact force of electrical connector may result in unsmooth insertion-extraction and excessive contact resistance and further cause contact failure. In order to improve the contact reliability of electrical connectors, the insertion-extraction and temperature rise properties of an electrical connector were discussed. In the investigation, first, the insertion-extraction force and temperature rise of the contactor were simulated by using ABAQUS. Then, the effect of clearance between spring and support frameδand angle of spring tongueαon the insertion-extraction force, as well as the influence of wire’s cross-sectional areaSand current on the temperature rise were revealed. Finally, the variations of insertion-extraction force and temperature rise were measured by experiments. The results show that (1) whenδ=0.12 mm, the insertion-extraction force increases with the increase ofα; while whenδ=0.18 mm, the insertion-extraction force first increases and then decreases with the increase ofα; (2)whenαis constant,the insertion-extraction force decreases with the increase ofδ; (3) the temperature rise of the contactor increases with the increase of current, but decreases with the increase of wire’s cross-sectional area; and (4) the insertion-extraction force and temperature rise obtained by experiments are consistent with those obtained by simulation.Comprehensively considering the insertion-extraction force and temperature rise, the optimal parameters for the connector are suggested asδ=0.12 mm andα=15°.Key words:electrical connector; contact resistance; insertion-extraction force; temperature rise; finite element simulation

2016-06-07

国家自然科学基金资助项目(51305408);河南省高等学校重点科研项目(15A460029);中国博士后科学基金资助项目(2015M582199);郑州大学青年骨干教师资助计划项目 Foundation items: Supported by the National Natural Science Foundation of China(51305408) and China Postdatoral Science Foundation(2015M582199)

贺占蜀(1985-),男,博士,副教授,主要从事先进制造与精密加工研究.E-mail:hezhanshu@qq.com

1000-565X(2017)04-0059-07

TM 503+.5

10.3969/j.issn.1000-565X.2017.04.009