HVDC逆变器动态无功需求峰值的快速近似计算*

夏成军 蓝海文 杜兆斌 周保荣 洪潮

(1.华南理工大学 电力学院， 广东 广州 510640； 2.南方电网科学研究院有限责任公司， 广东 广州 510663)

HVDC逆变器动态无功需求峰值的快速近似计算*

夏成军1蓝海文1杜兆斌1周保荣2洪潮2

(1.华南理工大学 电力学院， 广东 广州 510640； 2.南方电网科学研究院有限责任公司， 广东 广州 510663)

安装动态无功补偿装置有利于提高受端系统的电压稳定性.文中提出了一种大扰动后逆变器动态无功需求峰值快速近似计算方法，用于确定动态无功补偿装置容量.通过对直流控制系统的深入分析，确定故障恢复过程中的直流控制方式并保留起主要作用的直流控制环节；明确决定逆变器动态无功需求曲线的要素并分析其受故障程度的影响，阐明不同程度扰动下逆变器动态无功需求峰值相对固定的机理；忽略扰动程度的影响，对系统参数作适当处理，用一条峰值最大的动态无功需求曲线近似估算不同程度扰动后的动态无功需求曲线；对上述简化直流系统列写微分方程，求解出动态无功需求峰值；利用该估算值确定受端系统应该加装的动态无功补偿装置容量.楚穗直流PSCAD/EMTDC模型的仿真结果验证了逆变器动态无功需求峰值估算值的准确性和文中动态无功补偿装置容量设计方法的可行性.

逆变器；高压直流输电；动态无功；高压直流控制；近似计算

高压直流输电系统正常运行时换流器需要消耗的无功功率约为直流传输功率的40%～60%[1]，可以由换流站内的静态无功补偿装置补足.受端系统大扰动后换流器动态无功消耗快速大幅上升，无功需求峰值达到直流传输功率的70%～80%[2]，由于换流器分接头和并联滤波器组尚未响应，逆变站从交流系统吸收大量无功，可达直流传输功率的20%.对于有多回直流集中馈入受端系统的南方电网，交流系统对直流的支撑相对不足，同时，换流站间的强电气耦合使受端电网故障期间多回直流换流母线电压下降[3-7]，带来恢复期间的大量动态无功需求，电压稳定问题将相当严峻.配置动态无功补偿装置可以实时补偿换流器的动态无功需求，提高大扰动后受端系统的电压稳定性[8-10]，但如何确定装置容量是动态无功补偿设计面临的一个难题.

文献[10]中指出，静止无功补偿器(SVC)的最佳安装容量是逆变器动态无功需求峰值与稳态无功需求的差值，因此，深入研究大扰动后逆变器的动态无功需求峰值，是确定无功补偿装置容量的关键.目前对大扰动后直流系统动态无功特性的研究工作主要是采用时域仿真工具对仿真结果进行规律总结.文献[10]中对CIGRE标准模型进行多次仿真，拟合出逆变器无功需求峰值与扰动大小的关系曲线.文献[11-12]中通过仿真验证探讨了控制方式和各控制环节参数对逆变站动态无功特性的影响,文献[13]中采用类似的方法对整流站动态无功特性进行了分析.文献[14]中对楚穗直流的仿真研究表明，大扰动后逆变器的无功特性曲线几乎不受换流母线故障严重程度的影响.动态无功补偿装置容量应能满足不同程度扰动后逆变器的动态无功需求，采用上述文献的时域仿真方法虽然能准确地得到不同程度扰动后的逆变器最大动态无功需求峰值，但是必须搭建详细仿真模型并进行不同程度扰动下的多次仿真计算，工作量大且仿真耗时长.

文中分析了故障恢复过程中起主要作用的直流控制环节，阐明不同程度扰动下逆变器动态无功需求峰值相对固定的原因，提出了大扰动后逆变器动态无功需求峰值快速近似计算方法，用于解决受端电网动态无功补偿装置容量的确定问题.最后用楚穗直流PSCAD/EMTDC模型验证文中逆变器动态无功需求峰值估算值的准确性和动态无功补偿装置容量设计方法的可行性.

1 受端电网大扰动后逆变器动态无功需求峰值的估算

文献[10]中的研究表明，受端大扰动下恢复期间的动态无功需求峰值比小扰动大，更不利于系统电压稳定，因此文中重点研究大扰动下逆变器的动态无功特性.文中的大扰动是指受端电网发生严重的对称三相短路故障，其严重程度足以使整流站在故障期间因逆变侧换流母线电压过低而采用最小电流控制.

1.1 大扰动后恢复过程中的直流控制系统模型

1.1.1 故障恢复期间控制方式的确定

换流器采用的控制方式通常是多种基本控制方式的组合[15]，控制方式切换逻辑如图1所示，直流电流、整流侧直流电压、逆变侧直流电压和熄弧角实测值分别为Id,mes、Udr,mes、Udi,mes和γmes，整定值为Id,ref、Udr,ref、Udi,ref和γref，偏差为Id,err、Udr,err、Udi,err和γerr.αr为整流侧触发角，αi为逆变侧触发角.这种控制方式选择逻辑增大了建立数学模型的难度，可以根据恢复过程中运行电气量的特点明确换流器的控制方式.

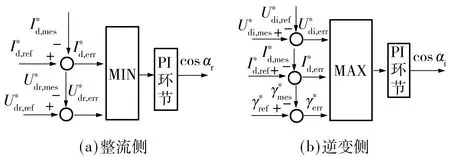
图1 楚穗直流换流站控制方式的切换逻辑

以楚穗直流为例，故障清除后初期，实测直流电压和电流很小，由于整流侧的电压整定值恒为1.3(p.u.)，而电流整定值在低压限流控制特性(VDCL)的作用下从最小直流电流IL升高到1(p.u.)，直流电压偏差比电流偏差大，整流侧采用定电流(VDCL)控制.逆变侧采用定直流电压控制的条件为

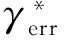
(1)

式中，Rci为逆变侧的等值换相电阻，n为换流站6脉动换流器的个数，Ei为受端换流母线电压，γref为17°,Udi,ref为800 kV，求解得到Udi,mes应大于703.196 kV(0.88(p.u.)).在故障恢复期间，直流电压未达到该值，直流电压偏差比熄弧角小，逆变侧采用定熄弧角控制.由于不同直流工程采用相似的参数，因此其他直流也采用相同的控制方式.

1.1.2 直流系统模型

控制方式明确后，直流系统控制框图如图2所示.直流系统由主要包含直流电流整定环节、PI环节的二次系统[16]、一次系统及完成一次系统和二次系统信号传递的测量环节和换流器组成.为了减少方程阶数，忽略一阶测量环节.

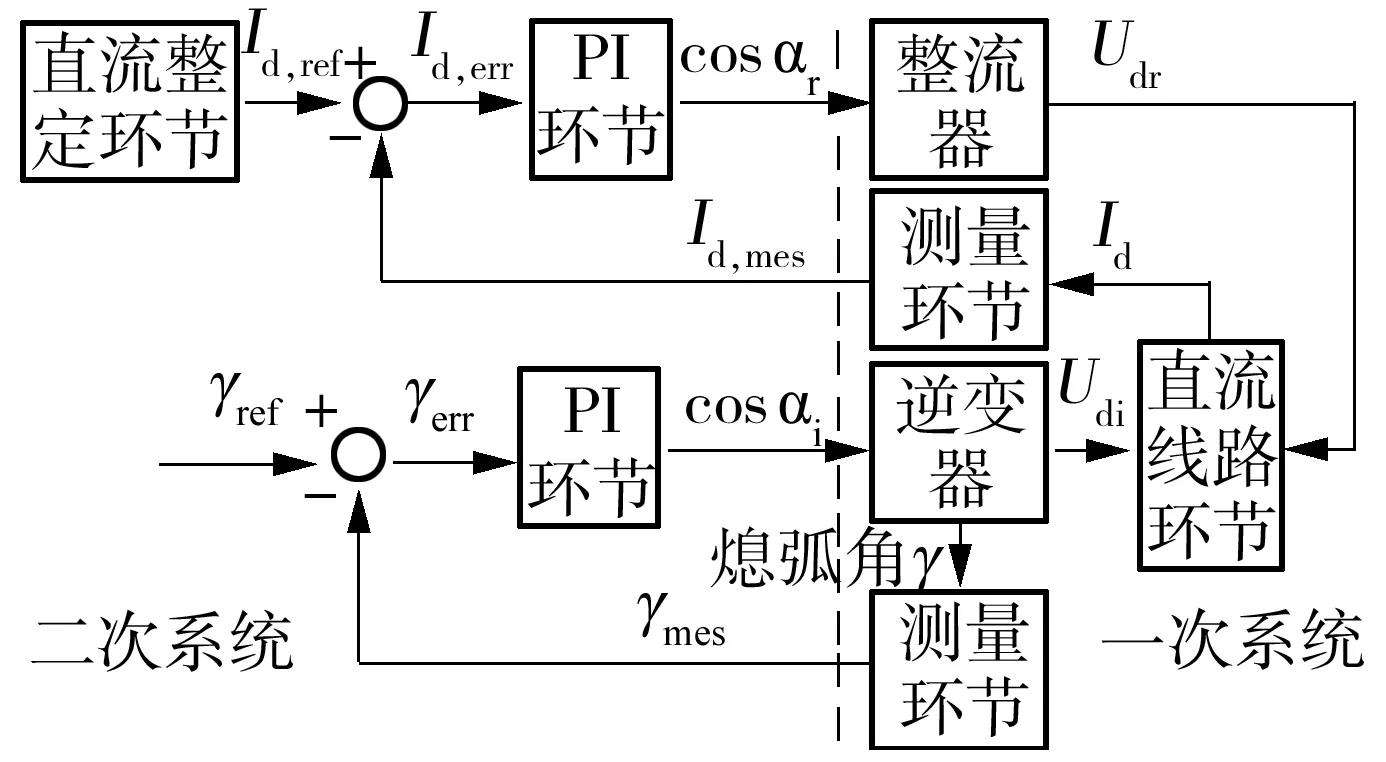
图2 恢复过程中直流系统的控制原理图

交流系统发生三相故障后，一次系统可以用准稳态模型表示[17]：

(2)

式中，αr(t)和αi(t)分别是送受端触发角，其余弦值为一次系统的输入，直流电流Id(t)和熄弧角γ(t)为一次系统的输出.一次系统的参数包括了换流站6脉动换流器的个数n、直流线路电阻RL、送受端等值换相电阻Rcr和Rci、受端换相电抗Xci以及随时间变化的母线电压Er(t)和Ei(t).

1.2 大扰动后逆变器动态无功需求峰值的特点

如图2所示，对于一条参数确定的直流系统，故障恢复过程中的动态无功曲线由系统输入(Id,ref、γref)、系统边值条件(故障消除瞬间和故障消除系统稳定后整流站和逆变站的触发角)和系统中的时变参数(Er(t)和Ei(t))唯一确定.受端系统发生不同严重程度的扰动后，若上述参数都很接近，则大扰动恢复期间的无功峰值将相对固定.

(1)系统中的时变参数

换流母线电压Er(t)和Ei(t)是系统随时间变化的参数.故障清除瞬间，直流传输功率开始爬升，换流器消耗无功小，滤波器组提供的无功过剩，即使换流母线故障程度不同，交流电压都能迅速恢复到额定值，故障程度对母线电压影响不大.随着换流器消耗无功增大到峰值后减小，母线电压先下降到谷值继而恢复到额定值，因此故障清除后，若系统电压稳定，交流电压在额定电压附近波动.忽略恢复期间交流电压波动，取Er(t)和Ei(t)为额定运行值，无功峰值估算结果与实际值相差不远.逆变侧交流系统越弱，无功需求峰值带来的压降越大，由于忽略了动态无功需求峰值会带来换流母线压降，取Er(t)和Ei(t)为额定运行值估算得到的无功需求峰值大于不同短路比下的无功需求峰值.

(2)系统边值条件

逆变侧换流母线发生不同程度的故障期间，由于逆变器发生换相失败，触发超前角β增大到其上限值βmax，因此在故障消除时刻逆变侧采用定β控制，整流侧定最小电流控制，故障清除时刻t0换流站的触发角满足如下公式：

(3)

稳态时触发角满足如下公式：

(4)

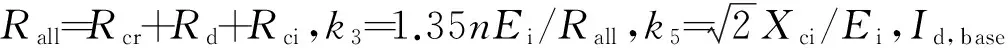
(3)系统输入

系统输入Id,ref是系统内部变量直流电压的非线性函数，如图3所示，其中Id,VDCL为VDCL输出的电流整定值，Id,HMI为后台电流指令.扰动程度越小，恢复期间直流电压更快达到VH，Id,ref更快上升到额定值.若不考虑直流电压的上升时间，等效为VH=0、VL=0，故障清除后，Id,VDCL从最小电流IL跃变为额定值，计及控制系统中的惯性环节，不同故障程度下的电流整定值与扰动程度无关，即

Id,ref=Id,base[1-(1-IL)e-(t-t0)/T]

(5)

式中，T为惯性环节时间常数.因此，直流电压上升速率越快，Id,ref受故障程度的影响越小.由于故障恢复期间交流电压因滤波器组注入系统的过剩无功上升较快，相应的直流电压上升速率也快，因此Id,ref受故障程度的影响较小，同时，用式(5)中的Id,ref求出的动态无功需求峰值与实际值相差不远.由于该Id,ref是电流整定值最大可能取值，用其求出的无功估算值大于不同故障程度下的无功需求峰值.

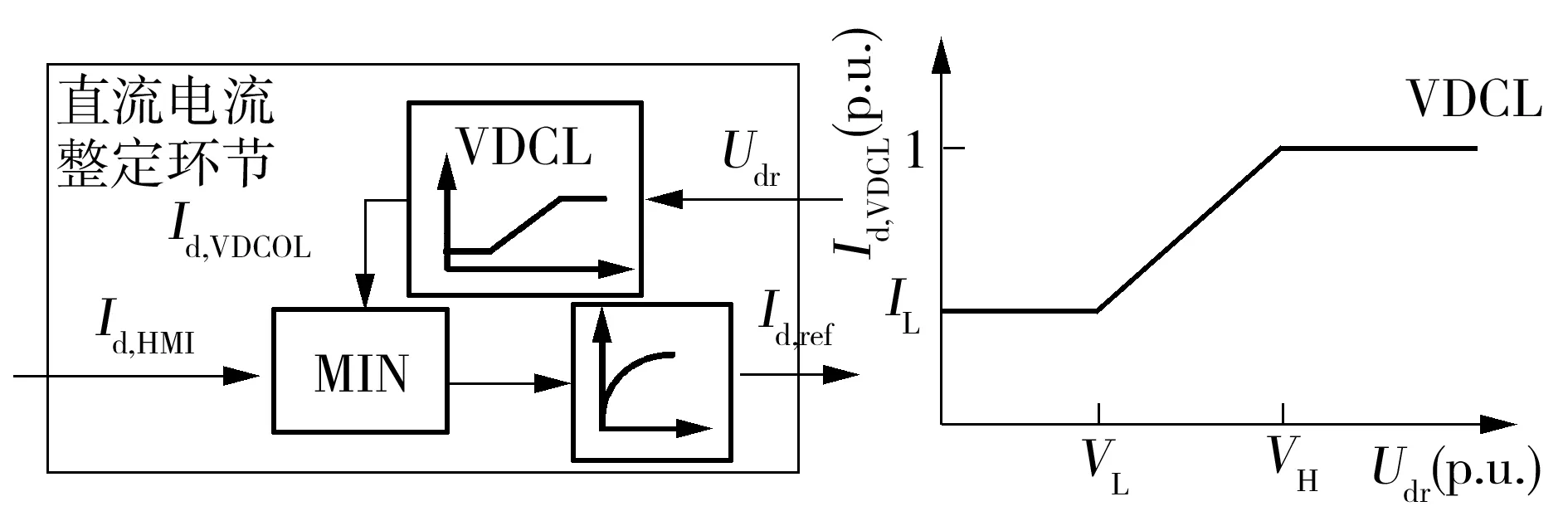
图3 直流电流整定环节

综上所述，换流母线发生不同严重程度故障后的恢复过程中，由于换流母线电压恢复较快，系统输入、系统边值条件和系统中的时变参数受故障严重程度的影响不大，动态无功需求峰值差异较小.同时，由于故障清除后实际交流电压在额定电压附近波动且直流电压上升速率快，用额定值代替交流电压和忽略直流电压上升时间，可以求出一条与不同程度扰动后动态无功特性近似的曲线，该曲线峰值理论上大于不同程度扰动后的动态无功需求峰值，也大于不同短路比下的无功需求峰值，保证估算的动态无功补偿装置容量能充分满足各种故障程度和运行方式下逆变站无功需求.

1.3 动态无功需求峰值的估算方法

(7)

联立式(5)-(7)，选取图4中的x1和x2作为状态变量，可以得到一个二阶微分方程组.为了简易地求解，近似认为式(6)中的cosαi(t)和式(7)中的Id(t)等于直流系统稳态运行时的值cosαi,s和Id,s，将原本的二阶状态方程变成两个一阶状态方程：

(8)

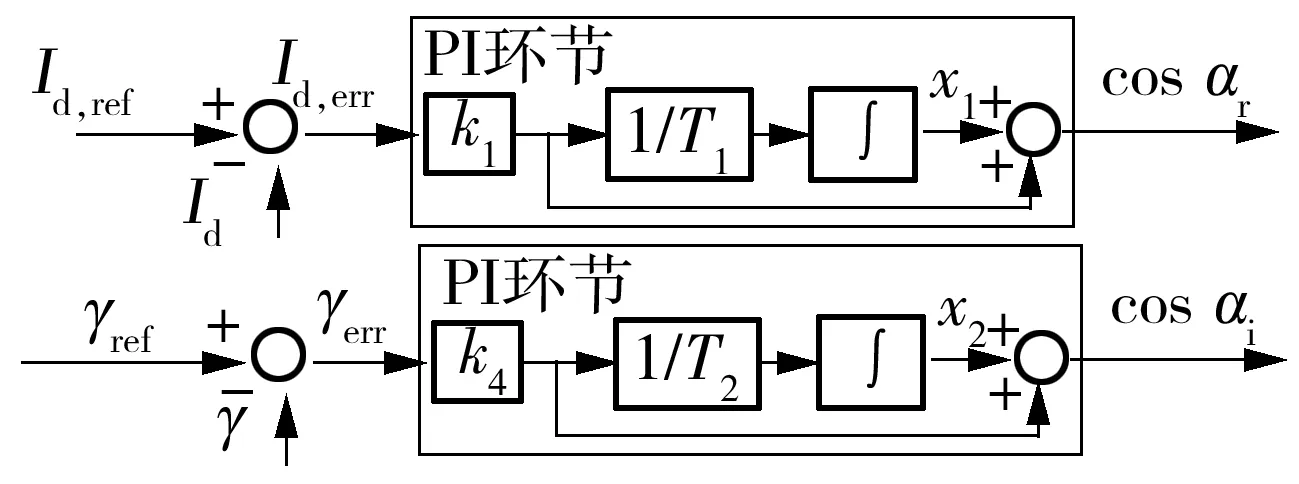
图4 PI环节

根据微分方程组(8)和边值条件(3)、(4)可以求解出无功特性曲线.

整流侧触发角余弦值为

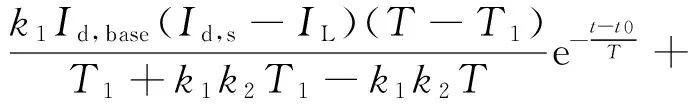
(9)

逆变站触发角余弦值为

(k5Id,sId,base-cosγref)

(10)

将式(9)和(10)代入式(11),可以得到大扰动后逆变器的动态无功需求曲线Qdi，求出峰值Qmax.

Qdi=1.35nEi(k2cosαr+k3k5Id,sId,base-k3cosγref)·

(11)

2 动态无功补偿装置容量设计

(1)动态无功补偿装置容量下限

短期大干扰电压稳定通常是由具有快速调节特性的负荷成分诸如感应电动机引起的[18]，文献[19]中给出的电压稳定判据表明，故障清除后，若感应电动机机端电压的极小值Umin小于感应电动机的小扰动稳定临界电压Usmin，电网可能发生暂态电压失稳.因此受端系统故障恢复期间，换流母线应保持较高电压.工程中认为，故障切除后，若母线电压低于0.75(p.u.)的时间持续超过1 s，则系统暂态电压失稳[20]，据此，可以将恢复过程中换流母线最低电压不小于0.75(p.u.)作为动态无功补偿装置容量下限的设计条件.受端(包括滤波器组)的戴维宁等效电路如图5所示.

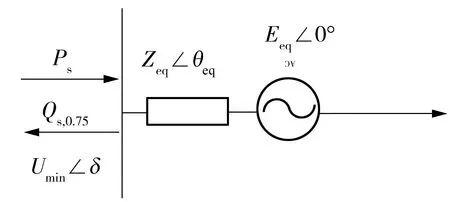
图5 受端交流系统戴维宁等效电路

图5中，Eeq∠0°和Zeq∠θeq分别为受端系统等值电源和等值阻抗，Umin∠δ为换流母线电压，Ps为注入受端系统的有功.

(12)

根据式(12)可以求出Umin=0.75(p.u.)时交流系统提供的无功Qs,0.75.当Qs,0.75小于第1节中求出的逆变器动态无功需求峰值Qmax时，换流母线最低电压将小于0.75(p.u.)，为了使换流母线最低电压达到0.75(p.u.)，这部分无功差额需由动态无功补偿装置补偿，即动态无功补偿装置容量下限Qdynmin为

Qdynmin=Qmax-Qs,0.75

(13)

(2)动态无功补偿装置容量上限

假设逆变器的动态无功需求被完全补偿，交流电压将达到额定值，滤波器输出的无功和稳态时相同，动态无功补偿装置的最佳安装容量Qdynmax应选取逆变器动态无功需求峰值Qmax与稳态值Qds之差：

Qdynmax=Qmax-Qds

(14)

由于逆变器的动态无功被完全补偿，当动态无功补偿装置容量大于该值时，电压不会有很大改善，同时造价也会提高.

3 仿真验证

3.1 楚穗直流逆变器动态无功需求峰值

以楚穗直流为例，通过与楚穗直流PSCAD/EMTDC模型的仿真结果进行对比，验证文中逆变器动态无功需求峰值估算方法的有效性.

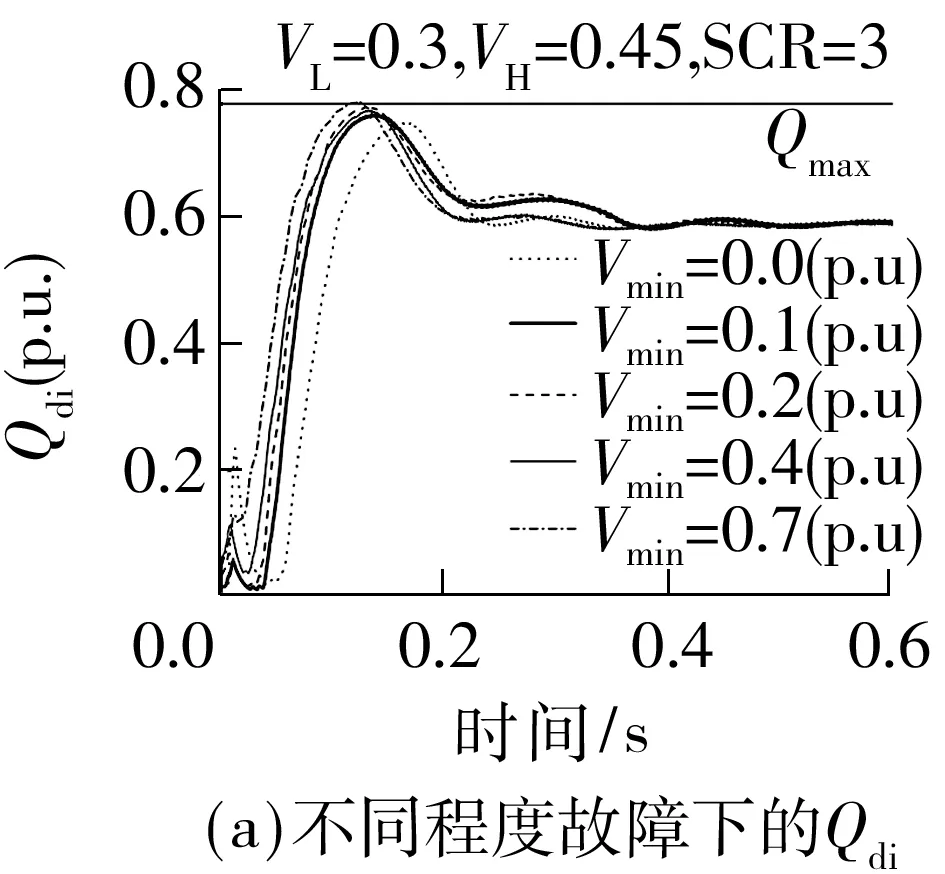
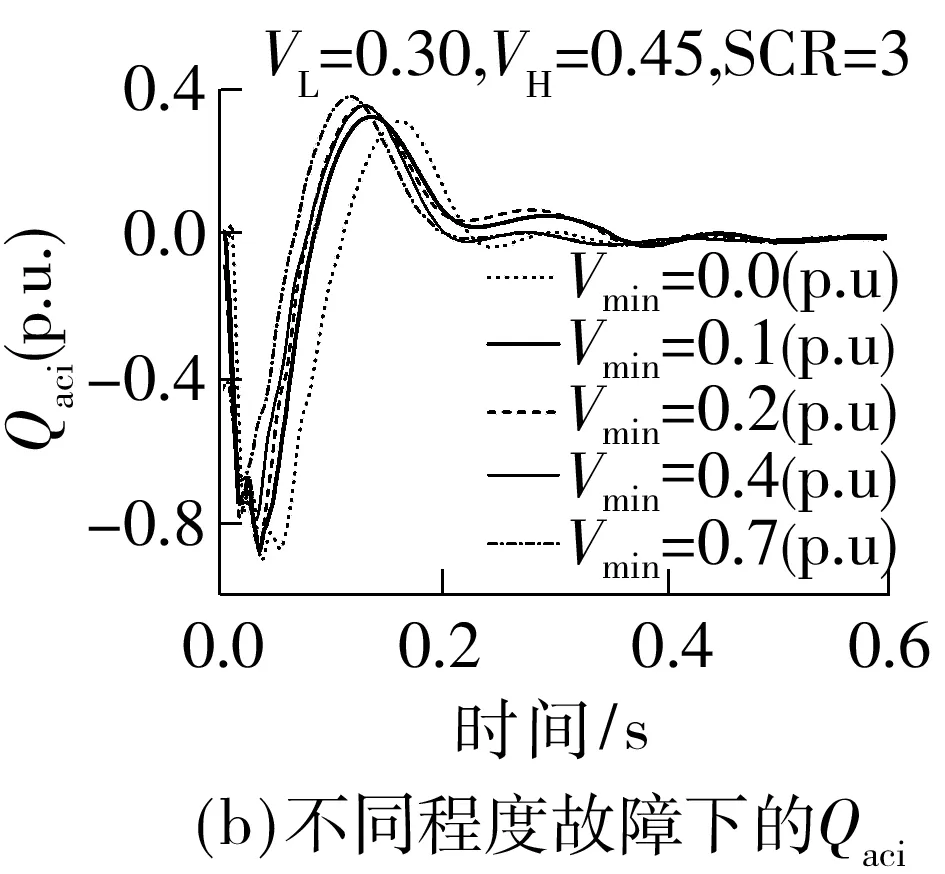
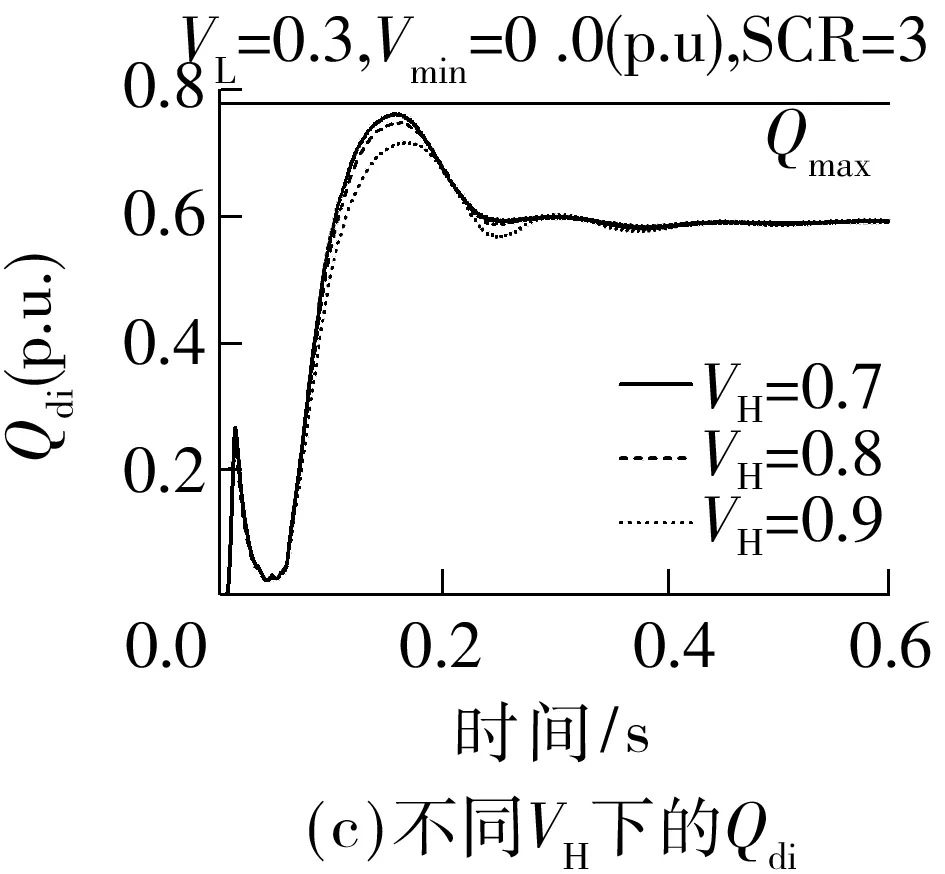
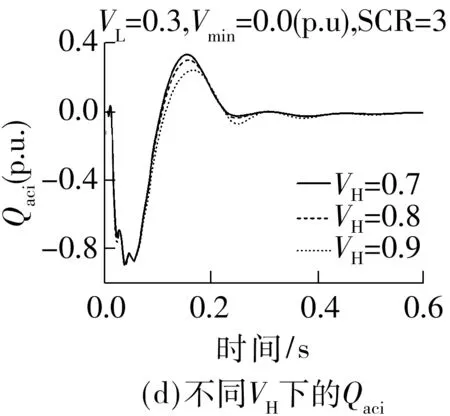
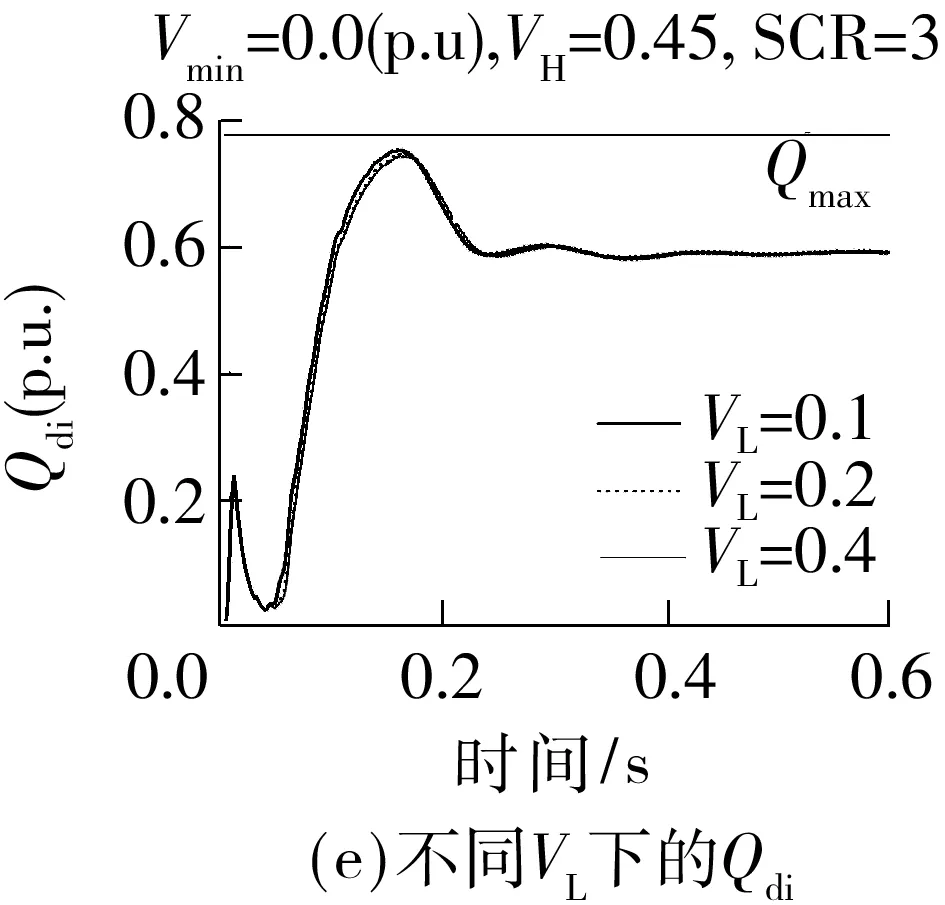
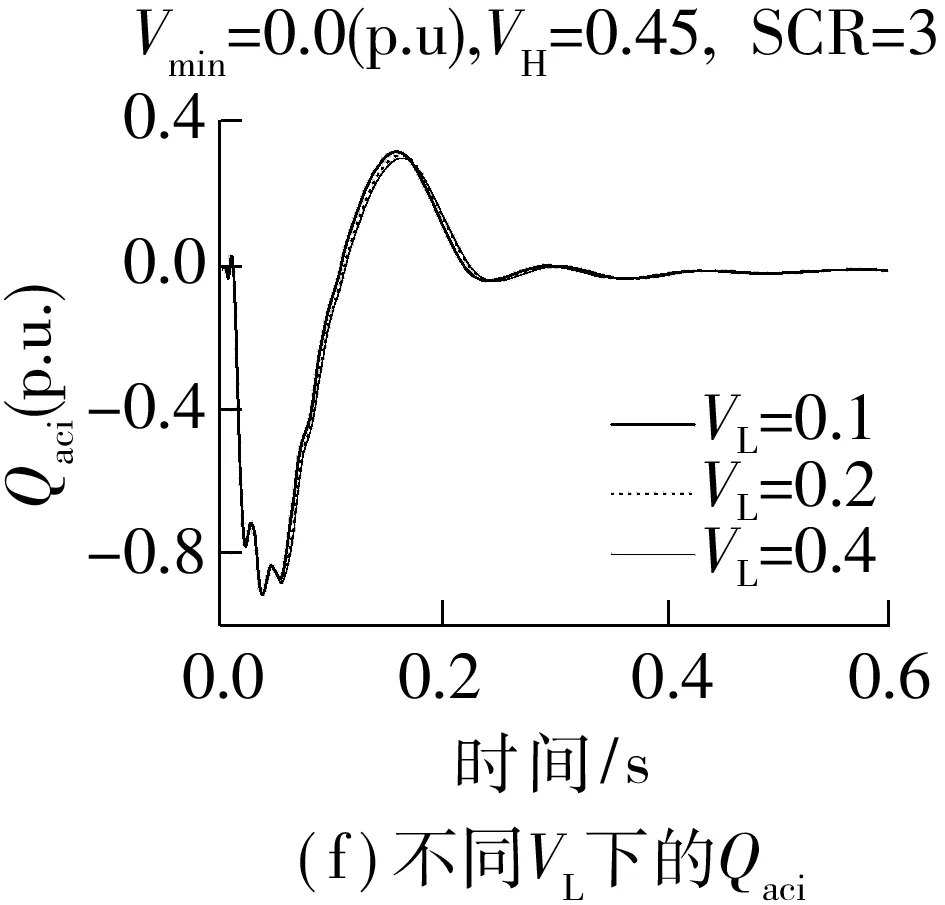
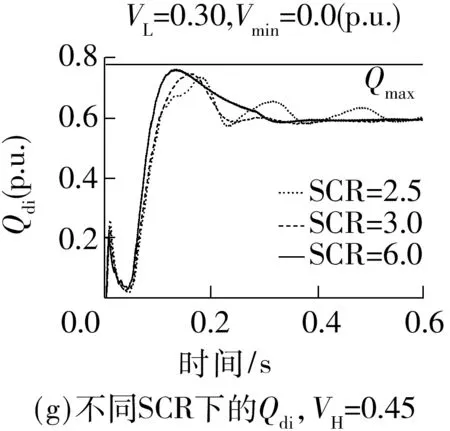
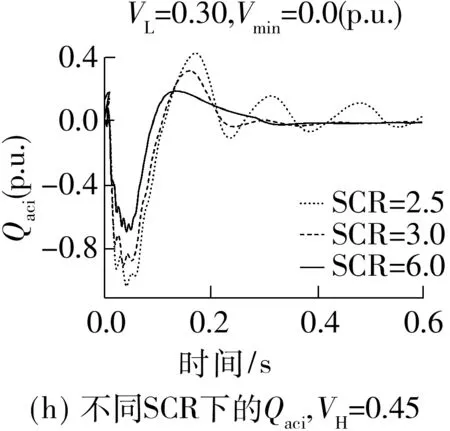
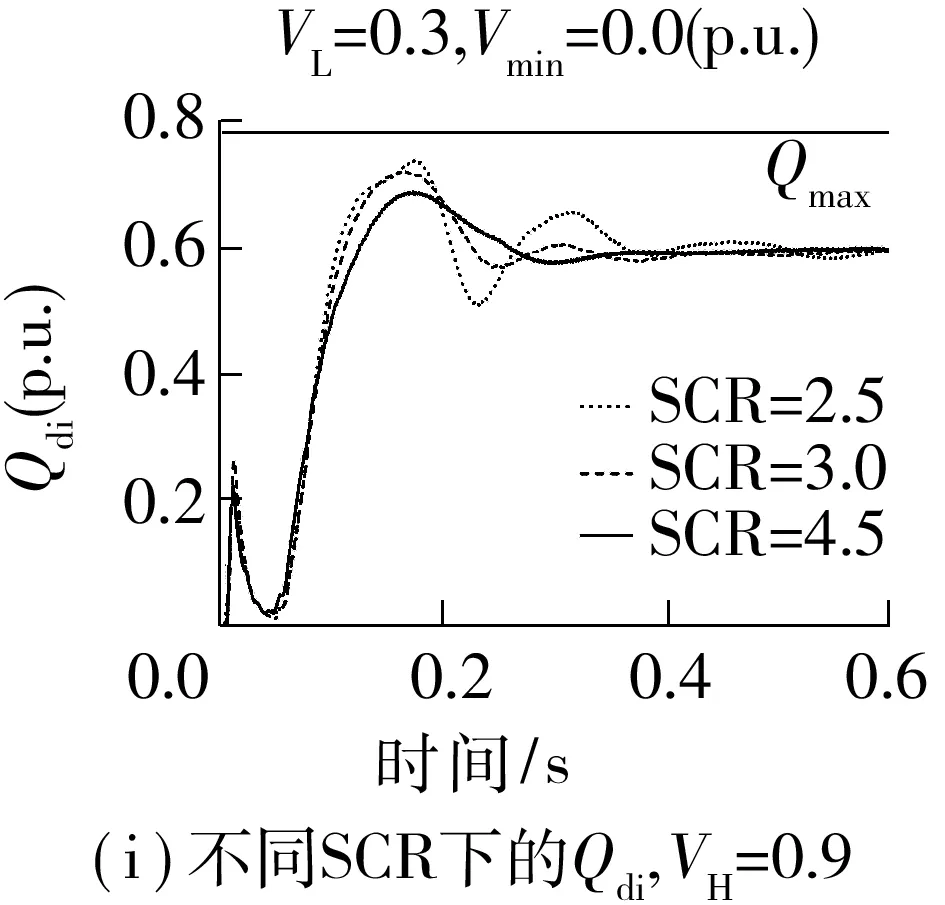
Fig.6 Simulation results of Chu-sui PSCAD/EMTDC model with different parameters

用文中方法估算得到的动态无功需求峰值为

Qmax=0.778 (p.u.),SB=5 000 MW.

改变仿真模型中的故障接地阻抗、VDCL参数和受端SCR，在受端换流母线设置100 ms三相短路故障，0 s故障清除，逆变器动态无功需求Qdi和逆变站从交流系统吸收的无功Qaci仿真曲线如图6所示，Vmin为故障期间换流母线最低电压.

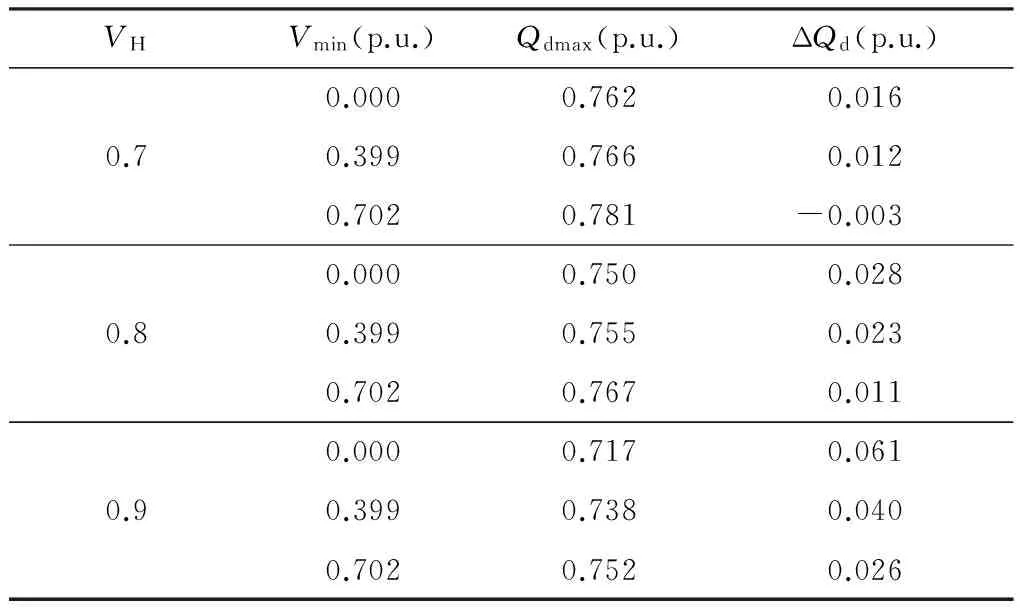
限于文章篇幅，文中只列出不同VH(SCR=3.0，VL=0.3)和VL(SCR=3.0，VH=0.45)下，受端换流母线发生不同严重程度的100 ms三相短路故障后的仿真结果，如表1、2所示(Qdmax为故障恢复期间逆变器动态无功需求峰值，ΔQd=Qmax-Qdmax).

表1 不同VH下PSCAD/EMTDC模型仿真结果与估算值

Table 1 Simulation results of Chu-Sui PSCAD/EMTDC model and estimation value with differentVH

VHVmin(p.u.)Qdmax(p.u.)ΔQd(p.u.)0.0000.7620.0160.70.3990.7660.0120.7020.781-0.0030.0000.7500.0280.80.3990.7550.0230.7020.7670.0110.0000.7170.0610.90.3990.7380.0400.7020.7520.026

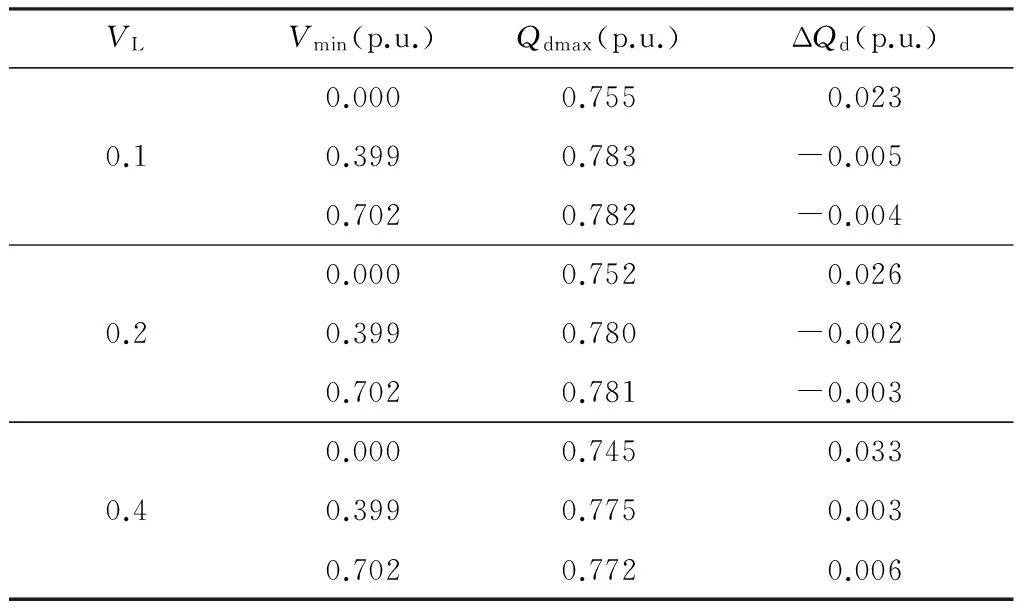
表2 不同VL下 PSCAD/EMTDC模型仿真结果与估算值

Table 2 Simulation results of Chu-Sui PSCAD/EMTDC model and estimation value with differentVL

VLVmin(p.u.)Qdmax(p.u.)ΔQd(p.u.)0.0000.7550.0230.10.3990.783-0.0050.7020.782-0.0040.0000.7520.0260.20.3990.780-0.0020.7020.781-0.0030.0000.7450.0330.40.3990.7750.0030.7020.7720.006

根据图6的Qdi曲线和表中数据可以得到以下结论：①不同程度扰动后的Qdmax差异较小，这是因为故障清除后换流母线电压恢复迅速，决定动态无功曲线的系统输入、系统边值条件和系统中的时变参数在不同扰动程度下都很接近；②随着VH和VL减小，相同程度扰动下Qdmax增大.文中仿真得到的Qdmax受VH和VL影响较小，这是因为文中选用短路比SCR=3.0的较弱系统，故障清除瞬间，交流电压因滤波器组注入系统的过剩无功上升速度较强系统更快，Id,ref对VH和VL的变化更不敏感；③对比图6(g)和图6(i)，Qdmax随SCR的变化趋势与VH和VL的取值相关.SCR越大，一方面，动态无功需求峰值带来的换流母线压降越小，使Qdmax越大；但另一方面，故障清除瞬间交流电压上升速率越慢，低压限流控制VDCL作用更显著，Id,ref越小，使Qdmax越小.随着VH和VL增大，当Id,ref减小程度超过换流母线压降减小程度时，Qdmax将从随SCR的增大而增大变成随SCR的增大而减小.取VH=0.0和VL=0.0时，Id,ref不随SCR改变，Qdmax随SCR增大而增大.

根据上述结论，为忽略故障程度对逆变器动态无功特性的影响，故障清除后令VH=0.0，VL=0.0，SCR=∞，估算得到的无功需求峰值Qmax是最大的，图6和表1、2中的仿真结果也表明Qmax基本大于不同故障程度下仿真得到的动态无功需求峰值，可用于估算弱系统下动态无功补偿装置容量，补偿动态无功缺额.

图6中Qaci曲线受VH和VL的影响与Qdi基本一致，但受SCR的影响略有差异.Qaci曲线峰值随SCR减小而增大，这是因为SCR越小，对应无功需求峰值时的换流母线电压越低，滤波器提供的无功越小，交流系统需要提供更多无功.

3.2 楚穗直流受端动态无功补偿装置容量设计

根据式(12)-(14)可以得到楚穗直流受端系统SCR为2.5时需要的动态无功补偿装置容量上、下限为

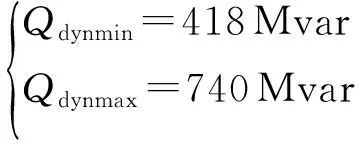
在楚穗直流PSCAD/EMTDC仿真模型受端换流母线上加装不同容量的STATCOM，并在受端换流母线上设置100 ms的三相接地故障，0 s故障清除，故障恢复期间的换流母线电压Ei如图7所示.

图7表明，随着STATCOM容量的增加，换流母线最低电压升高.当STATCOM提供的无功大于Qdynmin时，交流最低电压能达到0.75(p.u.)，避免电压暂态失稳；当STATCOM提供的无功大于Qdynmax时，最低换流母线电压不再随STATCOM提供无功的增大而增大.验证了文中所提出的动态无功补偿容量计算方法是合理的.仿真结果表明，文中方法对高肇直流和兴安直流也同样适用，因此该方法具有普适性，限于文章篇幅，此处略去仿真波形.

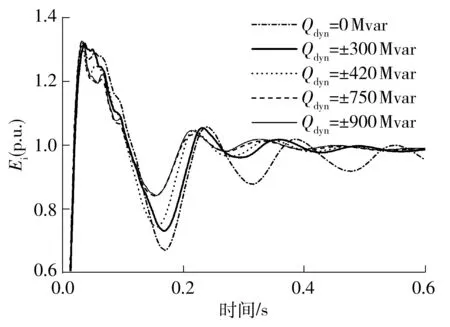
图7 不同STATCOM容量下的换流母线电压恢复曲线

Fig.7 Voltage of commutation bus with different capacity of STATCOM during recovery

对比图6(h)中对应工况下的Qaci曲线，Qdynmax远小于动态无功补偿装置未投入时换流站从交流系统吸收的无功峰值Qacimax(2 000 Mvar).这是因为动态无功补偿装置投入后的故障恢复过程中，与未投入时相比，交流电压更高，滤波器能提供的无功更多，动态无功缺额更少，因此动态无功补偿设备容量不需达到Qacimax.

4 结论

(1)受端换流母线受到不同程度的大扰动后，由于故障清除后换流母线电压迅速恢复，决定逆变器动态无功特性曲线的系统输入、系统边值条件和系统中的时变参数受故障严重程度的影响不大，恢复过程中逆变器动态无功需求峰值差异较小；

(2)由于动态无功补偿装置的电压支撑作用增大了故障恢复期间滤波器的无功输出，动态无功补偿设备的最佳补偿容量不需达到动态无功补偿装置未投入时换流站从交流系统吸收的无功峰值；

(3)文中提出了不同程度扰动后逆变器最大动态无功需求峰值快速近似计算方法，该曲线峰值能大于不同短路比下的无功需求峰值，解决了弱系统下受端电网动态无功补偿装置容量确定问题.与时域仿真方法相比，该方法不需要搭建详细直流仿真模型和进行多次不同程度扰动下的仿真计算，简便实用.

[1] 赵婉君．高压直流输电工程技术 [M]．北京：中国电力出版社，2010：173．

[2] 夏成军，梁国开，涂亮，等．HVDC受端换流站动态无功功率恢复特性及控制措施仿真 [J]．南方电网技术，2015，9(8)：57-63． XIA Cheng-jun，LIANG Guo-kai，TU Liang，et al．Simulation of recovery characteristics and control measures of dynamic reactive power of HVDC inverter station [J]．Southern Power System Technology，2015，9(8)：57-63．

[3] CIGRE Working Group B4.41．Systems with multiple DC infeed [R]．Paris：CIGRE，2008．

[4] DENIS Lee HauAik，GORAN Andersson.Voltage stability analysis of multi-infeed HVDC systems [J].IEEE Tran-sactions on Power Delivery，1997，12(3)：1309-1318．

[5] DENIS Lee HauAik，GORAN Andersson．Analysis of vol-tage and power interactions in multi-infeed HVDC systems [J]．IEEE Transactions on Power Delivery，2013，28(2)：816-824．

[6] 陈政，周保荣，洪潮，等．基于临界阻抗边界的多馈直流系统同时故障风险评估 [J]．电网技术，2013，37(3)：874-878. CHEN Zheng，ZHOU Bao-rong，HONG Chao，et al．Critical impedance boundary-based risk assessment on simulations faults in multi-infeed DC transmission system [J]．Power System Technology，2013，37(3)：874-878．

[7] 崔琪．多馈入直流系统的无功配置优化研究 [D]．保定：华北电力大学，2014．

[8] 徐式蕴，刘津，赵兵，等．藏中电网SVC配置方案及补偿策略分析 [J]．电网技术，2013，37(8)：2136-2142． XU Shi-yun，LIU Jin，ZHAO Bing，et al．Configuration scheme of static var compensation for central Tibet power grid and analysis on compensation strategy [J]．Power System Technology，2013，37(8)：2136-2142．

[9] 胡涛，刘翀，班连庚，等．藏中电网SVC控制策略实时仿真及参数优化 [J]．电网技术，2014，38(4)：1001-1007． HU Tao，LIU Chong，BAN Lian-geng，et al．Real-time simu-lation and parameter optimization of SVC control strategy for central-Tibet power grid [J]．Power System Technology，2014，38(4)：1001-1007．

[10] 张一荻．交直流受端电网动态无功需求特性与对策研究 [D]．广州：华南理工大学,2012．

[11] 杨欢欢，朱林，蔡泽祥，等．直流控制对直流系统无功动态特性的影响分析 [J]．电网技术，2014，38(10)：2631-2637． YANG Huan-huan，ZHU Lin，CAI Ze-xiang，et al．Influence of HVDC control on HVDC reactive power dynamic characteristic [J]．Power System Technology，2014，38(10)：2631-2637．

[12] 王贺楠，郑超，任杰，等．直流逆变站动态无功轨迹及优化措施 [J]．电网技术，2015，39(5)：1254-1260． WANG He-nan，ZHENG Chao，REN Jie，et al．Dynamic reactive power trajectory of HVDC inverter station and its optimization measures [J]．Power System Technology，2015，39(5)：1254-1260．

[13] 郑超，汤涌，马世英，等．直流整流站动态无功特性解析及优化措施 [J]．中国电机工程学报，2014，34(28)：4886-4896． ZHENG Chao，TANG Yong，MA Shi-ying，et al．Study on the dynamic reactive power characteristic of HVDC rectifier stations and optimization measures [J]．Proceedings of the CEEE，2014，34(28)：4886-4896．

[14] XIA Cheng-jun，LAN Hai-wen，MEN Kun，et al．Research on the transient power characteristics of the inverter for Yun-Guang UHVDC [J]．Journal of Power and Energy Engineering，2014，2(9)：176-181．

[15] 张勇军．高压直流输电原理与应用 [M]．北京：清华大学出版社，2012：127．

[16] 杨汾艳，徐政，张静．直流输电比例-积分控制器的参数优化 [J]．电网技术，2006，30(11)：15-20． YANG Fen-yan，XU Zheng，ZHANG Jing．Study on parameter optimization of HVDC PI controllers [J]．Power System Technology，2006，30(11)：15-20．

[17] 吴红斌，丁明，黄凯，等．交直流系统暂态仿真中换流器的改进准稳态模型 [J]．继电器，2003，31(10)：37-40． WU Hong-bin，DING Ming，HUANG Kai，et al．Modified quasi steady state model of converters in transient simulation of hybrid AC/DC systems [J]．Relay，2003，31(10):37-40．

[18] 井艳清，李兴源，郭晓鸣，等．考虑感应电动机负荷模型的暂态电压稳定快速判据 [J]．电力系统自动化，2011，35(5)：10-14． JING Yan-qing，LI Xing-yuan，GUO Xiao-ming，et al．A quick criterion for transient voltage stability considering induction motor load models [J]．Automation of Electric Power System，2011，35(5)：10-14．

[19] 孙华东．计及感应电动机负荷的电压稳定分析及其应用研究 [D]．北京：中国电力科学研究院，2005．

[20] 汪娟娟，张尧，夏成军，等．交直流电力系统暂态电压稳定性综述 [J]．电网技术，2008，32(12)：30-34． WANG Juan-juan，ZHANG Yao，XIA Cheng-jun，et al．Survey of studies on transient voltage stability of AC/DC power system [J]．Power System Technology，2008，32(12)：30-34．

Fast Proximate Calculation of Dynamic Reactive Power Peak Demand in Inverter of HVDC

XIACheng-jun1LANHai-wen1DUZhao-bin1ZHOUBao-rong2HONGChao2

(1.School of Electric Power, South China University of Technology, Guangzhou 510640, Guangdong, China;2. Electric Power Research Institute，CSG,Guangzhou 510663,Guangdong, China)

Dynamic reactive power compensation devices are effective in improving the voltage stability of the receiving end. In this paper, a fast proximate calculation method of dynamic reactive power peak demand in inverter after large disturbances is proposed to determine the capacity of dynamic reactive power compensation devices. In the investigation, first, the direct-current control mode is determined and the control links that play a major role in HVDC (High-Voltage Direct Current Transmission) during the failure recovery are retained after a detailed analysis of HVDC control system. Next, the elements that determine the dynamic reactive power characteristics of the inverter are defined and the impact of disturbance severity on the elements is analyzed, which helps to clarify the mechanism by which the peak value of dynamic reactive power consumption of the inverter is relatively fixed. Then, some system parameters are properly processed without considering the impact of disturbance severity to estimate the dynamic reactive power characteristics after different AC voltage drops with a unique peak curve. Moreover, the differential equitation describing the simplified HVDC system is presented and the dynamic reactive power peak demand is obtained. Finally, the estimated demand value is used to determine the capacity of the dynamic reactive power compensation device installed in the receiving power network. Simulated results on Chu-Sui HVDC PSCAD/EMTDC model show that the estimated dynamic reactive power peak is correct, and that the proposed design method of dynamic reactive poser compensation devices is feasible.

inverter; high-voltage direct current transmission; dynamic reactive power; HVDC control; proximate calculation

2016-03-18

国家自然科学基金资助项目(51577071)；广东省自然科学基金资助项目(2015A030313202) Foundation items: Supported by the National Natural Science Foundation of China(51577071) and the Natural Science Foundation of Guangdong Province(2015A030313202)

夏成军(1974-)，男，博士，副教授，主要从事电力系统稳定分析与控制、HVDC和FACTS研究.E-mail：cjxia@scut.edu.cn

1000-565X(2017)04-0008-07

TM 721

10.3969/j.issn.1000-565X.2017.04.002