高压直流系统无功动态对暂态电压稳定的影响*

蔡泽祥 冯雷 杨欢欢 朱林 张东辉 周保荣

(1.华南理工大学 电力学院， 广东 广州 510640； 2.南方电网科学研究院， 广东 广州 510080)

高压直流系统无功动态对暂态电压稳定的影响*

蔡泽祥1冯雷1杨欢欢1朱林1张东辉2周保荣2

(1.华南理工大学 电力学院， 广东 广州 510640； 2.南方电网科学研究院， 广东 广州 510080)

采用直流系统准稳态模型解析故障后高压直流输电系统无功的时域变化规律，并通过仿真深入分析其动态变化幅值和时间特性.通过对比分析考虑直流影响和不考虑直流影响两种情况，阐述了故障后直流系统无功动态对感应电动机无功恢复产生的延缓效应，揭示了直流系统无功动态影响暂态电压稳定的机理和途径.最后提出以感应电动机临界滑差变化率作为评估直流系统对暂态电压稳定影响的指标，并结合南方电网实际系统进行了验证.

高压直流输电；无功动态特性；暂态电压稳定；评估指标

暂态电压稳定问题与电力系统内的无功平衡有密切关系，系统中无功电源不足是导致暂态电压失稳的根本原因[1].直流系统无功动态改变了所接入的交流电网的无功平衡，其对交流电网暂态电压稳定的影响成为近年来的研究热点[2-3].

文献[4-5]中分别分析了不同故障形式和不同直流控制策略下直流系统中的换流器无功动态的时域特性，但目前关于直流系统整体的无功动态分析仍然缺乏.故障后的直流系统无功动态对交流电网暂态电压稳定的影响机理和途径也未形成清晰明确的结论.文献[6-7]中运用仿真手段分析了交直流系统中导致暂态电压失稳的主导因素，但主导因素的作用机制仍不清晰.文献[8-13]中从直流控制的角度定性分析了直流系统对交流电网暂态电压稳定的影响并提出了控制优化策略，但由于暂态电压失稳的根本原因是电力系统的无功电源无法满足无功负荷的需求，所以仅从直流控制的角度无法揭示直流系统对暂态电压失稳的影响机理和途径.

短路比(SCR)和多馈入短路比(MSCR)分别表示单直流馈入和多直流馈入时交流系统与直流系统的相对强弱关系，目前被广泛用于直流系统对交流电网暂态电压稳定影响的初步评估[14-15].但由于短路比和暂态电压稳定间没有严格的理论关系，其准确性有时得不到保证.

针对上述问题，文中基于直流系统准稳态模型对故障后直流系统无功动态的时域变化规律进行详细分析，并以云广特高压直流为背景，通过仿真着重研究直流系统无功动态的幅值和时间特性.接着对比考虑直流和不考虑直流两种情况下感应电动机的无功变化，发现故障后直流系统无功动态延缓了感应电动机的无功恢复，从而对交流电网的暂态电压稳定产生影响.最后，提出以感应电动机临界滑差变化率作为直流系统无功动态对暂态电压稳定影响的评估指标，并结合南方电网实际系统验证了该指标的有效性.

1 直流系统无功动态时域解析

1.1 基于准稳态模型的时域解析

根据直流系统准稳态模型，逆变侧的无功功率平衡关系式[16]为

(1)

Id=(Udr-Udi)/R

(2)

(3)

(4)

(5)

(6)

(7)

f(α,μ)=

(8)

式中:Uac、k、N、Xc、R分别为换流母线电压、换流变变比、每极桥数、等效换相电抗和直流线路电阻；α、γ、 μ、φ分别为触发角、熄弧角、换相重叠角和功率因数角；Qd为换流器消耗的无功功率,简称换流器无功；Qc为滤波器和无功补偿的无功功率，简称补偿无功;B为并联补偿的等效电纳；Qa为直流系统从交流系统吸收的无功功率，简称直流系统无功；Udr、Udi、Id分别为整流侧直流电压、逆变侧直流电压、直流电流.

逆变侧α范围为(90°,150°)，Uac标幺值范围为[0,1]，Id标幺值范围为(0,2)，此时f(α,μ)约等于1.Qa可化简为

(9)

稳态时，Qc基本补偿Qd，Qa基本为0，即有

(10)

逆变侧采用定熄弧角控制，含低压限流环节的直流系统，短路故障发生后，Uac下降，Udi随之减小，直流电流Id增大，Qa大于0.随后受低压限流控制影响，Id逐渐下降，Qa随之减小到较小数值.故障切除瞬间，Uac上升，Id因Uac上升而减小，Qa小于0.随后，因低压限流的折线特性，Id逐渐上升，由于Uac尚未恢复到额定值，换相重叠角μ较大，受定熄弧角控制的影响，为保持γ不变，触发角α较小，故Id较大，Qa大于0.

综上可知，直流系统无功Qa在故障发生后整体呈现“先正后负再正”的趋势，其性质以“无功负荷-无功电源-无功负荷”的规律变化.

1.2 直流系统无功动态仿真分析

以南方电网云广特高压直流为背景，利用电力系统仿真软件PSD-BPA构建典型的交直流系统仿真模型，对上节结论进行验证.模型如图1所示，直流系统采用云广特高压直流的实际模型及参数，双极额定功率5 000 MW，额定电压±800 kV，额定电流3.125 kA；交流电网采用三角形结构以模拟直流落点处的等值交流系统，发电机和负荷是交流电网中的电源支撑和功率消耗，z1、z2、z3表示交流电网中电源、负荷和换流母线之间的电气距离；发电机采用经典二阶模型；负荷采用50%感应电动机+50%恒阻抗的综合负荷模型，总大小为6 000 MW+j2 Gvar.

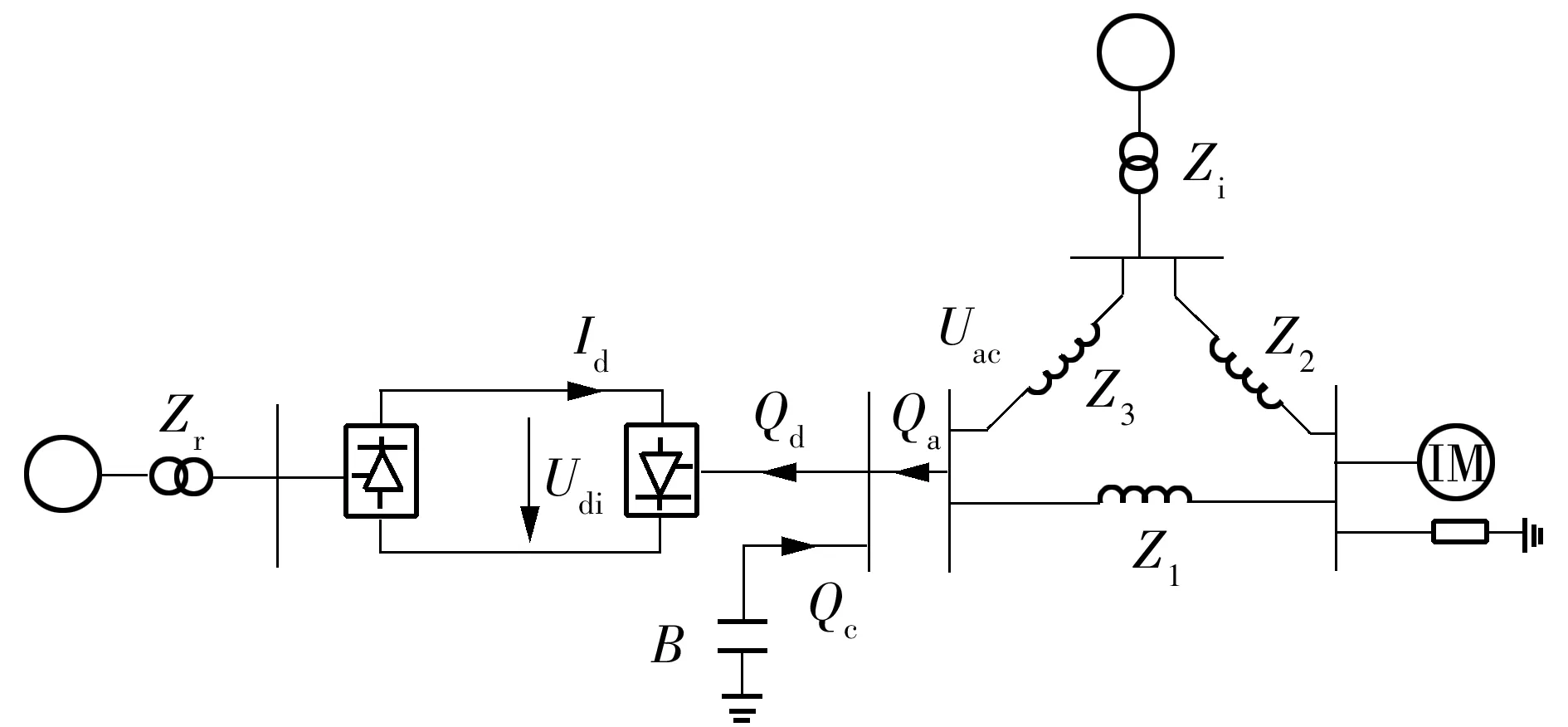
图1 交直流系统仿真模型

图2是交流系统三相故障导致逆变站换流母线电压跌到0.35(p.u.)时直流系统无功的响应特性曲线.

图2 逆变站无功变化

由图2可知，直流系统无功以“无功负荷-无功电源-无功负荷”的规律变化，与1.1节结论相符.根据直流系统无功在动态过程中的性质，将直流系统无功动态分为故障期间、恢复前期和恢复后期3个阶段.下面进一步分析这3个阶段直流系统无功的幅值和时间特性.图3为负荷母线三相短路故障时，不同故障切除时间下直流系统的无功曲线，其中tcl=0.460 2 s，为临界暂态电压稳定切除时间.

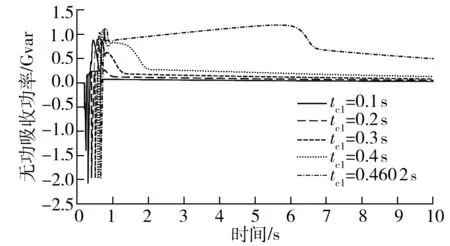
图3 不同故障切除时间下的直流系统无功吸收功率

Fig.3 Reactive power of HVDC system under different clearing time condition

由图3可知：①故障期间，无功幅值与其他两个阶段相比处于较低的水平，该阶段的持续时间与故障切除时间相同；②恢复前期，无功幅值明显地高于其他两个阶段，但该阶段的持续时间极短；③恢复后期，无功幅值随着故障切除时间的增加而增加，尤其在故障切除时间较大时，无功幅值增加幅度会比较大，该阶段的无功幅值明显高于故障期间的水平，持续时间亦随着故障切除时间增加而增加，且在故障切除时间接近临界暂态电压稳定切除时间时，该阶段的持续时间会迅速上升，远高于其余两个阶段.

综上可知，直流系统在恢复前期往交流系统注入无功时，无功幅值虽然大，但持续时间极短，对系统的影响有限.故障期间和恢复后期直流系统均从交流系统吸收无功，但恢复后期直流系统无功的幅值和阶段持续时间都要明显高于故障期间，因此恢复后期直流系统的无功动态对系统的影响受到更大关注.

2 直流系统无功动态对暂态电压稳定的影响分析

2.1 影响机理分析

暂态电压稳定表示系统在故障后短期内维持所有节点电压的能力，研究表明暂态电压稳定问题与感应电动机行为有密切关系[17]，直流系统无功动态对暂态电压稳定的影响很大程度上取决于直流系统与感应电动机的相互作用.图4是感应电动机等值电路及其等价变换.

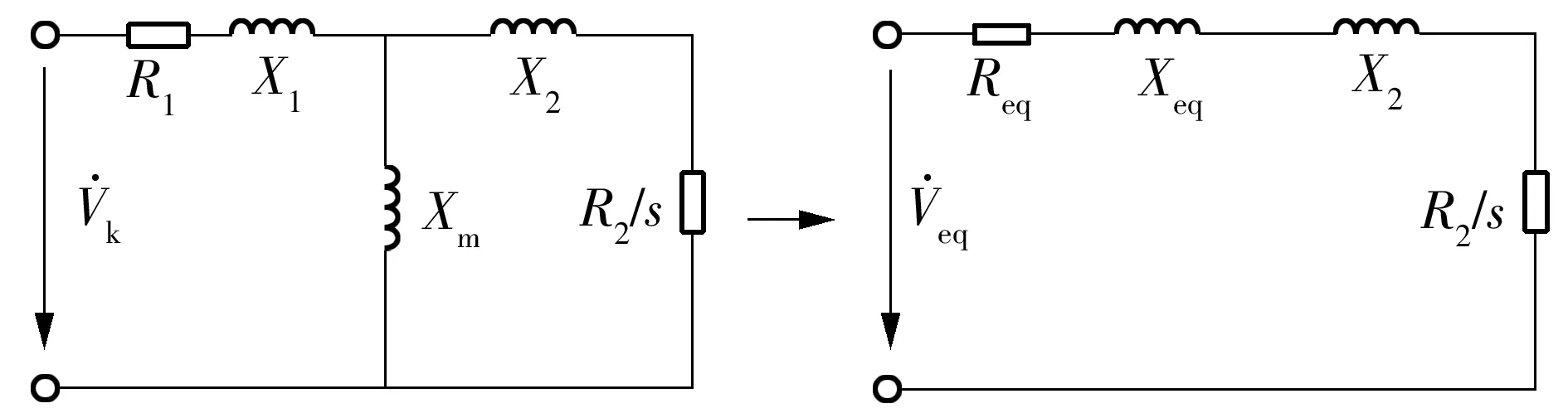
图4 感应电动机等值电路

感应电动机的运动方程和电路方程[18]为

(11)

式中，Tj为惯性时间常数，s为滑差，Tm、Te、Pe、Ω1分别为电动机的负载转矩、电磁转矩、电磁功率和同步转速，Vk为电动机端电压，Q为电动机吸收的无功，R1、X1、R2、X2、Xm分别为电动机定子电阻、定子电抗、转子电阻、转子电抗和励磁电抗.下面分析两种情况的暂态电压稳定性：①考虑直流影响，即直流系统正常运行；②不考虑直流影响，即直流系统停运，并在换流母线注入一定有功维持初始潮流不变.

负荷母线三相短路时，接于该母线的感应电动机在故障期间Te为0，若故障切除时间为tcl，对式(11)中的运动方程两边同时积分，得故障切除瞬间滑差s：

s=s0+Tmtel/Tj

(12)

式中，s0为电动机的初始滑差，由上式可知故障切除时间相同时，故障切除瞬间两种情况下接于故障母线的感应电动机s相同，故障母线的负荷阻抗相等.对于其他负荷母线，分为两种情形：①负荷母线距离故障点较近时，接于该母线的电动机Te近似为0，滑差仍可用式(12)表示，故考虑直流影响和不考虑直流影响两种情况下母线的负荷阻抗相等；②负荷母线距离故障点较远时，受故障影响小，其负荷阻抗近似为恒定阻抗，两种情况下母线的负荷阻抗依然相等.设Z为包含负荷阻抗的节点阻抗矩阵，则故障切除瞬间两种情况的Z相同.由于恢复前期持续时间极短，负荷阻抗变化不大，恢复后期初Z在两种情况下仍近似相等.此时根据网络方程有

(13)

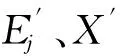
(14)

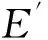
图5 Te-s曲线

若故障切除时间较长，感应电机滑差st接近scr，由图5可知，不考虑直流影响情况下，电动机仍有较大的加速转矩，由式(11)可知,s可迅速恢复，相应地Q也可迅速恢复；考虑直流影响情况下,Te与Tm十分接近，加速转矩几乎为0，由式(11)知此时滑差s恢复速度十分小，所需的恢复时间将长许多，因恢复速度慢，滑差长时间保持为故障切除后的较大值，电动机无功Q也相应地长时间维持在高水平，只有待滑差恢复后电动机无功才会恢复，即直流系统无功动态对感应电动机无功恢复产生延缓效应.

(15)

故障切除瞬间，由于s较大，集合M中的电动机吸收大量无功，Qq为绝对值较大的负值，因而故障切除瞬间Vn较小，故障切除后，不考虑直流影响情况下Qq迅速恢复，使得Vn得以迅速恢复；考虑直流影响情况下由于延缓效应电动机无功Qq恢复缓慢，导致Vn恢复缓慢，暂态电压稳定性变差.

综上所述，直流系统无功动态降低了感应电动机的端电压，减小了感应电动机的加速转矩，从而对感应电动机无功恢复产生延缓效应，恶化了交流电网的暂态电压稳定性.

2.2 仿真验证

下面结合仿真说明上述机理过程.令图1所示系统负荷母线三相短路，故障切除时间tcl为0.460 2 s，考虑直流影响和不考虑直流影响两种情况下，感应电动机的Vk、Pe、s和Q在恢复后期中的变化曲线如图6所示.

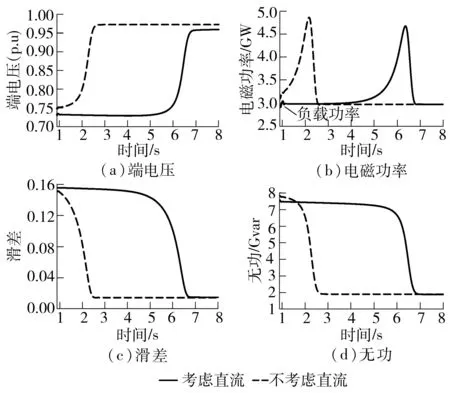
图6 感应电动机端电压、电磁功率、滑差和无功

Fig.6 Voltage,electromagnetic power,slip and reactive power of induction motor

由图6知，与不考虑直流的情况相比，考虑直流情况下感应电动机端电压较低，加速功率几乎为0，滑差s和无功Q在故障切除后无法迅速恢复至故障前水平，直流系统无功动态对感应电动机无功恢复产生延缓效应.图7为相应情况的各母线电压.

图7 各母线电压

由图7可知，由于直流系统无功动态对感应电动机无功恢复的延缓效应，各母线电压恢复所需时间明显更长，暂态电压稳定性更差.仿真结果验证了上述机理的正确性.

3 基于临界滑差变化率的评估指标

感应电动机滑差和无功消耗能否恢复直接决定了系统电压能否恢复，因此感应电动机稳定与暂态电压稳定在一定程度上具有一致性.感应电动机滑差是否超过临界滑差是感应电动机是否失稳的判据.图8是感应电动机临界稳定和临界失稳时滑差和负荷母线电压变化曲线.

图8 临界情况下滑差和负荷母线电压变化曲线

Fig.8 Slip and voltage of load bus change curve under critical conditions

由图8可知：故障切除后，如果感应电动机滑差小于临界滑差，则滑差能恢复到稳定平衡点，负荷母线电压可以恢复；如果感应电动机滑差大于临界滑差，则滑差不断增大，负荷母线暂态电压失稳.感应电动机的临界滑差在某种程度上是对系统暂态电压稳定性的衡量，因此直流系统无功动态特性对暂态电压稳定的影响可通过临界滑差变化率r表示：

(16)

式中，scr为直流系统运行时的感应电动机临界滑差，scr0为相同潮流条件下直流系统停运时的感应电动机临界滑差.

短路比SCR表示了交流系统与直流系统的相对强弱关系，一般认为SCR越小，交流系统相对直流系统越弱.下面分析在不同SCR下临界滑差变化率随直流系统无功的变化情况.在图1所示系统中，改变受端电网线路阻抗使受端交流系统SCR分别为5和8，在负荷母线设置三相短路故障，改变直流功率(P=0，500，1 000，1 500，1 800，2 000，2 200，2 500MW)，临界滑差变化率随恢复后期中直流系统无功吸收峰值的变化关系如图9所示.

图9 临界滑差变化率-直流系统无功吸收峰值曲线

Fig.9Criticalslipchangingrate-reactivepowerpeakcurvesofHVDCsystem

由图9可知，随着直流系统无功吸收峰值的增加，临界滑差变化率负增长，暂态电压稳定性变差.直流系统无功吸收峰值相同时，SCR较大条件下，临界滑差变化率的绝对值较小.这是因为SCR较大时，受端系统电源维持电压的能力更强，削弱了直流系统无功吸收对暂态电压稳定的影响.该结果证明了评估指标的有效性.

以上是在单一直流条件下得出的结论，下面进一步分析多直流条件下的情况.采用南方电网数据模型，负荷采用60%感应电动机+40%恒阻抗并等值到500 kV母线上.分别在各直流落点附近设置三相短路故障，改变相应直流功率(P从0变化至额定功率)，得到临界滑差变化率随恢复后期直流系统无功吸收峰值的变化曲线，如图10所示.多直流馈入时，一般采用多馈入短路比MSCR表示交流系统与直流系统的相对强弱.表1为南方电网各直流的MSCR.

由图10可知，随着直流系统无功吸收峰值的增加，临界滑差变化率呈近似线性下降.直流系统无功吸收峰值相同时，临界滑差变化率的绝对值基本上随着MSCR增大而减小.该结果进一步验证了评估指标的有效性.

图10 南方电网各直流无功动态对暂态电压稳定的影响

Fig.10 Influence of each HVDC in China Southern Power Grid on short-term voltage stability

表1 南方电网各直流MSCR

需要指出的是，与直接采用MSCR评估相比，采用临界滑差变化率评估直流系统对暂态电压稳定的影响显示出更好的效果.表2是各直流系统额定功率下的临界滑差变化率.

表2 南方电网各直流额定功率下的临界滑差变化率

Table 2 Critical slip changing raterof each HVDC in CSG at rated power

直流名称兴安直流糯扎渡高肇直流三广直流云广直流溪洛渡天广直流r/%-4.6-5.7-3.7-1.6-7.6-15.1-11.4

对比表1和2，直流系统额定功率下临界滑差变化率的绝对值没有随着MSCR增大而减小.例如对于溪洛渡直流，其MSCR大于天广直流，但临界滑差变化率的绝对值更大.原因可以从图10解释，虽然溪洛渡直流MSCR更大，但其无功吸收峰值远大于天广直流，使得其落点处的暂态电压稳定性变化更大.MSCR仅仅表示交流系统与直流系统容量上的强弱关系，与MSCR相比，临界滑差变化率更加准确地评估了直流系统对暂态电压稳定的影响程度.综上可知，临界滑差变化率是评估直流系统无功动态对暂态电压稳定影响的有效指标.

4 结论

交流系统发生短路故障后，直流系统无功动态按性质分为故障期间、恢复前期和恢复后期3个阶段，其中恢复后期的直流系统无功对交流系统表现为无功负荷，与其余两个阶段相比，无功幅值大且持续时间长，对交流电网的暂态电压稳定有较大的影响.恢复后期直流系统的无功动态延长了交流电网感应电动机滑差和无功的恢复时间，恶化了交流电网的暂态电压稳定性.感应电动机在暂态电压失稳过程中起决定性作用，含直流馈入的交流电网暂态电压稳定和感应电动机稳定具有一致性，感应电动机的临界滑差变化率可以有效评估直流系统无功动态对交流电网暂态电压稳定的影响.

[1] PRABHA Kundur．Power system stability and control [M]．北京：中国电力出版社，2002．

[2] 汪娟娟,张尧,夏成军,等.交直流电力系统暂态电压稳定性综述 [J].电网技术,2008,32(12):30-34. WANG Juan-juan，ZHANG Yao，XIA Cheng-jun,et al.Survey of studies on transient voltage stability of AC/DC power system [J].Power System Technology,2008,32(12):30-34.

[3] 林伟芳,汤涌,卜广全.多馈入交直流系统电压稳定性研究 [J].电网技术,2008,32(11):7-12. LIN Wei-fang,TANG Yong,BU Guang-quan.Study on voltage stability of multi-infeed HVDC power transmission system [J].Power System Technology,2008,32(11):7-12.[4] 张一荻.交直流受端电网动态无功需求特性与对策研究 [D].广州:华南理工大学,2012.

[5] 杨欢欢,朱林,蔡泽祥,等.直流控制对直流系统无功动态特性的影响分析 [J].电网技术,2014,38(10):2631-2637. YANG Huan-huan,ZHU Lin,CAI Ze-xiang,et al．Influence of HVDC control on HVDC reactive power dynamic characteristic [J].Power System Technology,2014,38(10):2631-2637．

[6] 廖民传,蔡广林,张勇军.交直流混合系统受端电网暂态电压稳定分析 [J].电力系统保护与控制,2009,37(10):1-4. LIAO Min-chuan,CAI Guang-lin,ZHANG Yong-jun.Transient voltage stability of received power grid in AC/DC hybrid power systems [J].Power System Protection and Control,2009,37(10):1-4.

[7] 秦文丽.多直流馈入受端电网电压稳定判据与控制措施研究 [D].北京:北京交通大学,2012.

[8] 李妮,李兴源,冯明,等.改善多馈入直流系统电压无功特性的直流控制策略 [J].电力自动化设备,2016,36(2):25-31. LI Ni,LI Xing-yuan,FENG Ming,et al.DC control for improving voltage and reactive power characteristics of multi-infeed HVDC system [J].Electric Power Automation Equipment,2016,36(2):25-31．

[9] 张建设,张尧,张志朝,等.直流系统控制方式对大扰动后交直流混合系统电压和功率恢复的影响 [J].电网技术,2005,29(5):20-24. ZHANG Jian-she,ZHANG Yao,ZHANG Zhi-chao,et al.Influence of DC system control modes on voltage and po-wer recovery after large disturbance in hybrid AC/DC system [J].Power System Technology,2005,29(5):20-24.

[10] 刘晓明,慈文斌,刘玉田.直流控制方式对受端电网电压稳定性影响 [J].电力自动化设备,2011,31(4):69-73. LIU Xiao-ming,CI Wen-bin,LIU Yu-tian.Influence of DC system control mode on voltage stability of receiving-end power grid [J].Electric Power Automation Equipment,2011,31(4):69-73.

[11] 郑超,盛灿辉,林俊杰,等.特高压直流输电系统动态响应对受端交流电网故障恢复特性的影响 [J].高电压技术,2013,39(3):555-561. ZHENG Chao,SHENG Can-hui,LIN Jun-jie,et al.Influence of UHVDC transmission system dynamic response on AC receiving end’s failure recovery characteristics [J].High Voltage Engineering,2013,39(3):555-561.

[12] 郑超,马世英,盛灿辉,等.以直流逆变站为动态无功源的暂态电压稳定控制 [J].中国电机工程学报,2014,34(34):6141-6149. ZHENG Chao,Ma Shi-ying,SHENG Can-hui,et al.Transient voltage stability control based on the HVDC inverter station acting as dynamic reactive source [J].Proceedings of the CSEE,2014,34(34):6141-6149.

[13] 王珂,杨胜春,姚建国,等.考虑无功功率协调控制的并行直流系统紧急功率支援 [J].电力系统自动化,2011,35(18):103-107. WANG Ke，YANG Sheng-chun，YAO Jian-guo.Emergency DC power support with reactive power coordinated control for multi-circuit HVDC systems [J].Automation of Electric Power Systems,2011,35(18):103-107.

[14] 王鹏飞,张英敏,陈虎,等.直流输电系统临界短路比的研究 [J].华东电力,2011(11):1780-1783. WANG Peng-fei,ZHANC Ying-min,CHEN Hu,et al.Criti-cal short circuit ratio of DC transmission system [J].East China Electric Power,2011(11):1780-1783.

[15] 林伟芳,汤涌,卜广全.多馈入交直流系统短路比的定义和应用 [J].中国电机工程学报,2008,28(31):1-8. LIN Wei-fang,TANG Yong,BU Guang-quan.Study on voltage stability of multi-infeed HVDC power transmission system [J].Power System Technology,2008,28(31):1-8.

[16] Siemens Industry Inc.PSS/E 33.5 program application guide volume 2 [R].[S.l.]：Siemens Industry Inc,2013:287-377.

[17] 井艳清,李兴源,郭晓鸣,等.考虑感应电动机负荷模型的暂态电压稳定快速判据 [J].电力系统自动化,2011,35(5):10-14. JING Yan-qing,LI Xing-yuan,GUO Xiao-ming,et al.A quick criterion for transient voltage stability considering induction motor load models [J].Automation of Electric Power System,2011,35(5):10-14.

[18] 李佳,刘天琪,李兴源,等.感应电动机模型和机械转矩参数对暂态电压稳定评估的影响 [J].电力系统保护与控制,2014,42(12):19-24. LI Jia,LIU Tian-qi,LI Xing-yuan,et al.Influence on assessment of transient voltage stability by induction motor model and mechanical torque parameters [J].Power System Protection and Control,2014,42(12):19-24.

Influence of Reactive Power Dynamics of HVDC System on Short-Term Voltage Stability

CAIZe-xiang1FENGLei1YANGHuan-huan1ZHULin1ZHANGDong-hui2ZHOUBao-rong2

(1.School of Electric Power, South China University of Technology, Guangzhou 510640, Guangdong, China;2.Electric Power Research Institute of China Southern Power Grid, Guangzhou 510080, Guangdong, China)

In this paper, first, the post-fault HVDC (High-Voltage Direct Current Transmission) reactive power change laws in time domain are analyzed by using the quasi-steady model of HVDC system. Next, the amplitude and time features of reactive power change are explored through simulation. Then, by comparatively analyzing the reactive power change with or without HVDC, the reactive power recovery delaying effect that HVDC reactive power dynamics exert on the induction motor is illustrated, and the mechanism and pathway by which HVDC reactive po-wer dynamics influence the short-term voltage stability are explored. Finally, an index, namely the change rate of critical slip of induction motor, is proposed to evaluate the influence of HVDC reactive power dynamics on the short-term voltage stability, and the effectiveness of the proposed method is verified by an application example on China Southern Power Grid.

high-voltage direct current transmission; reactive power dynamic characteristic; short-term voltage stability; evaluation index

2016-05-12

国家自然科学基金资助项目(51407079) Foundation item: Supported by the National Natural Science Foundation of China(51407079)

蔡泽祥(1960-)，男，教授，博士生导师，主要从事电力系统保护、控制与自动化研究.E-mail:epzxcai@scut.edu.cn

1000-565X(2017)04-0001-07

TM 711

10.3969/j.issn.1000-565X.2017.04.001