压电-电磁复合动能采集器无量纲参数建模与分析

夏桦康， 陈仁文， 朱莉娅， 任 龙， 周秦邦

(1.南京航空航天大学 机械结构力学及控制国家重点实验室，南京 210016;2.南京师范大学 江苏省三维打印装备与制造重点实验室，南京 210042)

压电-电磁复合动能采集器无量纲参数建模与分析

夏桦康1， 陈仁文1， 朱莉娅2， 任 龙1， 周秦邦1

(1.南京航空航天大学 机械结构力学及控制国家重点实验室，南京 210016;2.南京师范大学 江苏省三维打印装备与制造重点实验室，南京 210042)

针对压电-电磁复合动能采集器的物理参数模型难以提供统一的性能比较标准，以及最大输出功率及最优负载直接求解困难等问题。通过引入无量纲参数建立了采集器的无量纲参数模型，理论推导了归一化输出功率，并采用遗传算法求解了最大输出功率及最优负载；数值分析了无量纲参数对采集器性能的影响，并实验验证了模型和遗传算法求解的正确性。结果表明：①减小线圈负载可提升性能；②增大机械品质因子将提高频率选择能力；③当压电和电磁均为弱耦合作用时，性能受二者共同影响，且在二者匹配时获得最优；④当电磁为强耦合作用时，性能基本只受电磁端影响，且随其增强而不断趋近最优；⑤压电-电磁双耦合机制可增大采集器的最优负载范围。

能量采集；压电-电磁；无量纲参数模型；遗传算法

环境振动能量采集技术可以将振动能转换成电能，用以给无线传感器节点等低功耗电子设备供电，是当前一大研究热点。目前常见的动能采集器都是基于单一机电转换机制，如压电式动能采集器、电磁式动能采集器和静电式动能采集器，其中，关于前两种采集器的研究较多。压电式动能采集器输出电压较大，但输出电流较小，其输出阻抗呈容性；电磁式动能采集器输出电压较小，但输出电流较大，其输出阻抗呈感性[1]。除此之外，单一机电转换机制的动能采集器输出功率和转换效率较低，且工作频带和负载范围较窄。目前，国内外已有学者将多种机电转换机制集成到单个动能采集器中，从而构成复合式动能采集器。Challa等[2]设计了一种悬臂梁式的压电-电磁复合动能采集装置，该采集器在共振频率下收集到电功率332 μW，其性能比单一机电转换机制的采集器提高了近30%。Shan等[3]基于集总参数模型建立单自由度的压电-电磁复合动能采集器的数学模型，推导了采集器的理论输出功率，并从数值仿真和实验两方面验证了压电-电磁复合动能采集技术的优势。Wang等[4]设计了一种两自由度的压电-电磁复合动能采集装置，实现了两个相接近的共振频率点，从而实现了频带的扩展和功率的提升。Li等[5]对压电-电磁复合动能采集器的耦合作用进行了研究，揭示了采集器在弱耦合、中耦合与强耦合作用下的性能表现，其研究成果可为采集器的优化设计提供理论依据。蔡华通等[6]建立了压电-电磁复合动能采集器的集总参数物理模型，并研究了结构材料的物理参数对采集器性能的影响。上述两位学者采用的模型都忽略了线圈电感的影响，因此高频振动时模型误差相对较大。由于绝大多数研究采用的是物理参数模型，导致采集器性能与其物理尺寸、固有频率、材料特性等诸多物理参数直接相关，各采集器之间由于缺少统一标准而无法进行公平的性能比较。除此之外，关于压电-电磁复合动能采集器的最大输出功率及最优负载的求解也鲜有提及。

本文通过引入七个无量纲参数，建立了压电-电磁复合动能采集器的全要素无量纲参数模型，并推导了采集器的归一化输出功率表达式，给不同尺度的采集器提供了统一的性能比较标准。同时，针对压电-电磁复合动能采集器最大输出功率和最优负载直接求解困难等问题，本文提出了基于遗传算法的快速求解方法，并进行了数值仿真与分析，从而揭示了无量纲参数对采集器最大归一化输出功率的影响规律。最后，制作了一台单自由度悬臂梁式压电-电磁复合动能采集器样机并进行了实验，以验证理论的正确性。

1 压电-电磁复合动能采集器结构

图1所示的是一种单自由度悬臂梁式的压电-电磁复合动能采集器。悬臂梁表面粘贴有压电元件，同时在其自由端装配线圈以配合基座上的永磁体。当采集器在外界激励下发生受迫振动，压电元件由于受到交变应力将会输出交变电压，而闭合线圈由于其中磁通量发生变化也将产生交变电流。前者是基于正压电效应，后者是基于法拉第电磁感应定律，通过将这两种机电转换机制集成到单个动能采集器中，就构成了本文重点研究的压电-电磁复合动能采集器。

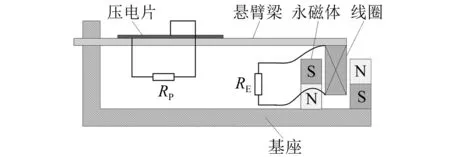
图1 单自由度悬臂梁式压电-电磁复合动能采集器结构示意图Fig.1 Single degree of freedom cantilever-based piezoelectric-electromagnetic hybrid vibration energy harvester

假设基础激励为简谐运动，基座运动位移为y，角频率为w，悬臂梁自由端与基座之间的相对运动位移为u，从而建立如下系统运动微分方程[7-8]：

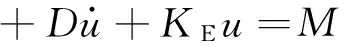
(1)

式中：M为系统等效质量；D为系统等效阻尼系数；KE为压电元件电学短路时的系统等效刚度；α为压电元件等效力压转换因子；β为电磁线圈等效力流转换因子；VP为压电元件输出电压；IE为电磁线圈输出电流。

2 理论推导

2.1 采集器功率推导

当压电元件和电磁线圈输出端口分别接入两个纯电阻负载RP和RE时，根据基尔霍夫电学定律建立电学方程如下：

(2)

(3)

式中：CP为压电元件等效夹持电容；r和Lc为电磁线圈的内阻和电感。

对式(1)，式(2)和式(3)进行零初始条件下的拉普拉斯变换并化简，得到悬臂梁自由端相对运动位移U(s)与基础激励加速度(s)之间的传递函数关系如下：

(4)

压电-电磁复合动能采集器输出功率等于消耗在两个纯电阻负载RP和RE上的电功率之和，则输出功率可以表示为悬臂梁自由端相对运动位移幅值uM的表达式：

(5)

将式(4)代入式(5)，可以得到用基础激励加速度幅值γM表示的输出功率表达式：

(6)

2.2 无量纲参数模型推导

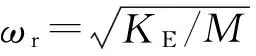
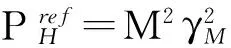
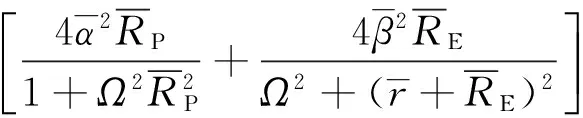
(7)表1 无量纲参数定义Tab.1 Definitions of the dimensionless parameters

3 采集器性能分析与优化

3.1 数值仿真与分析

压电-电磁复合动能采集器的归一化输出功率可用式(7)表示，由此可见：在采集器本体参数确定的情况下，采集器的性能受到压电输出端负载RP和电磁输出端负载RE的共同影响；因此当两个负载取得一个最优组合时，采集器的性能可达到最优。由于表达式(7)形式复杂，难以直接求得最优解析解，因此本文采用遗传算法进行最优负载的搜索以快速求得最优数值解[10]。为了提高种群中最佳个体密度和加快算法收敛速度，算法采用了最优保存策略和轮盘赌选择方法，算法流程，如图2所示。

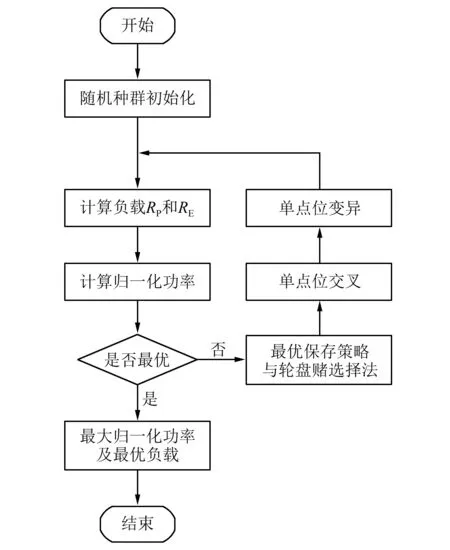
图2 基于遗传算法的最大输出功率求解流程图Fig.2 Power optimization process based on genetic algorithm

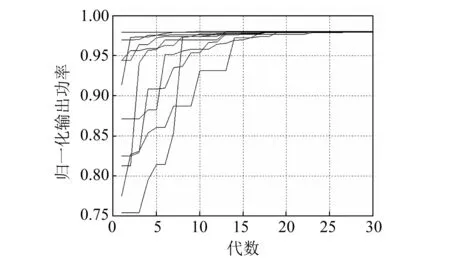
图3 遗传算法仿真曲线Fig.3 The simulation waveforms of genetic algorithm

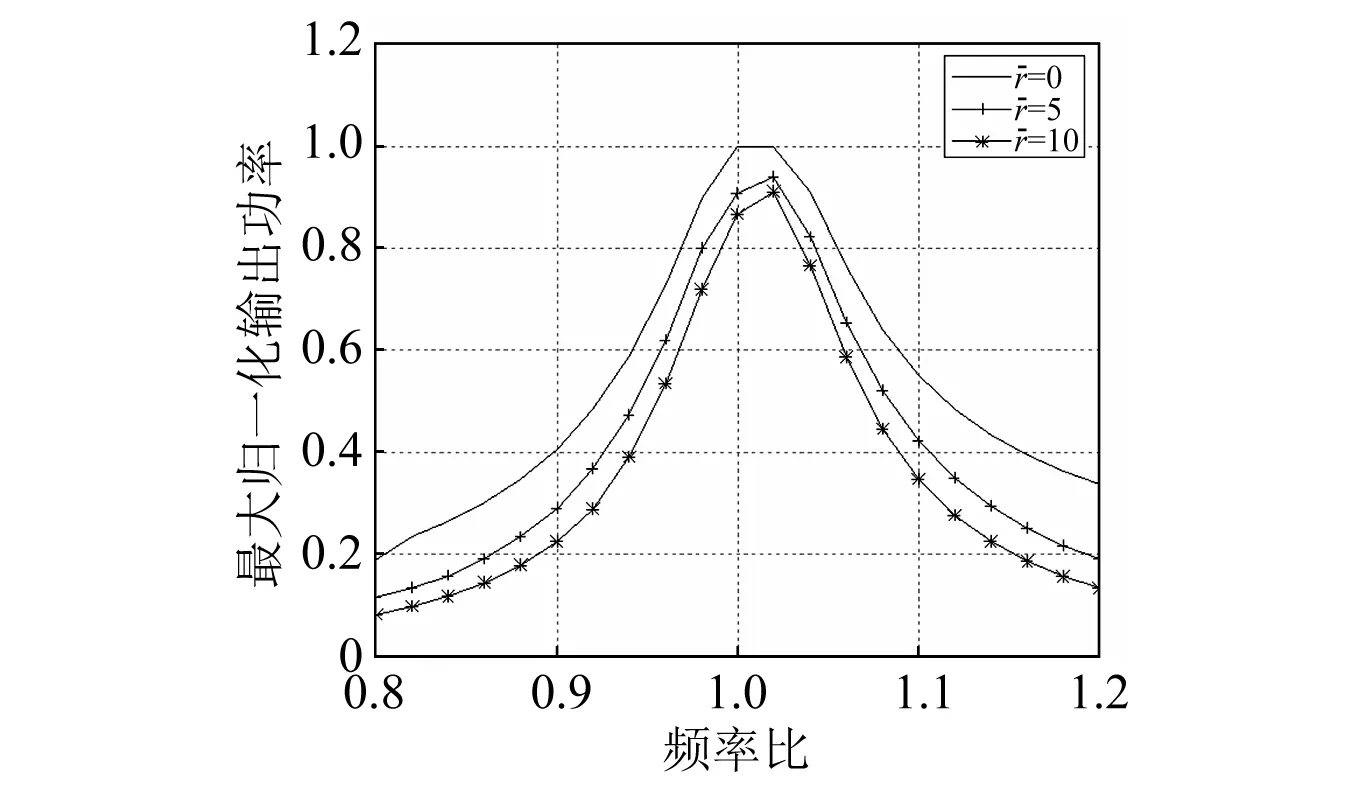
图4 不同值时，最大归一化输出功率随频率比变化仿真曲线Fig.4 The theoretical maximum normalized power as a function of frequency ratio under different values of

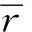
图5 不同QM值时，最大归一化输出功率随频率 比变化仿真曲线Fig.5 The theoretical maximum normalized power as a function of frequency ratio under different values of QM

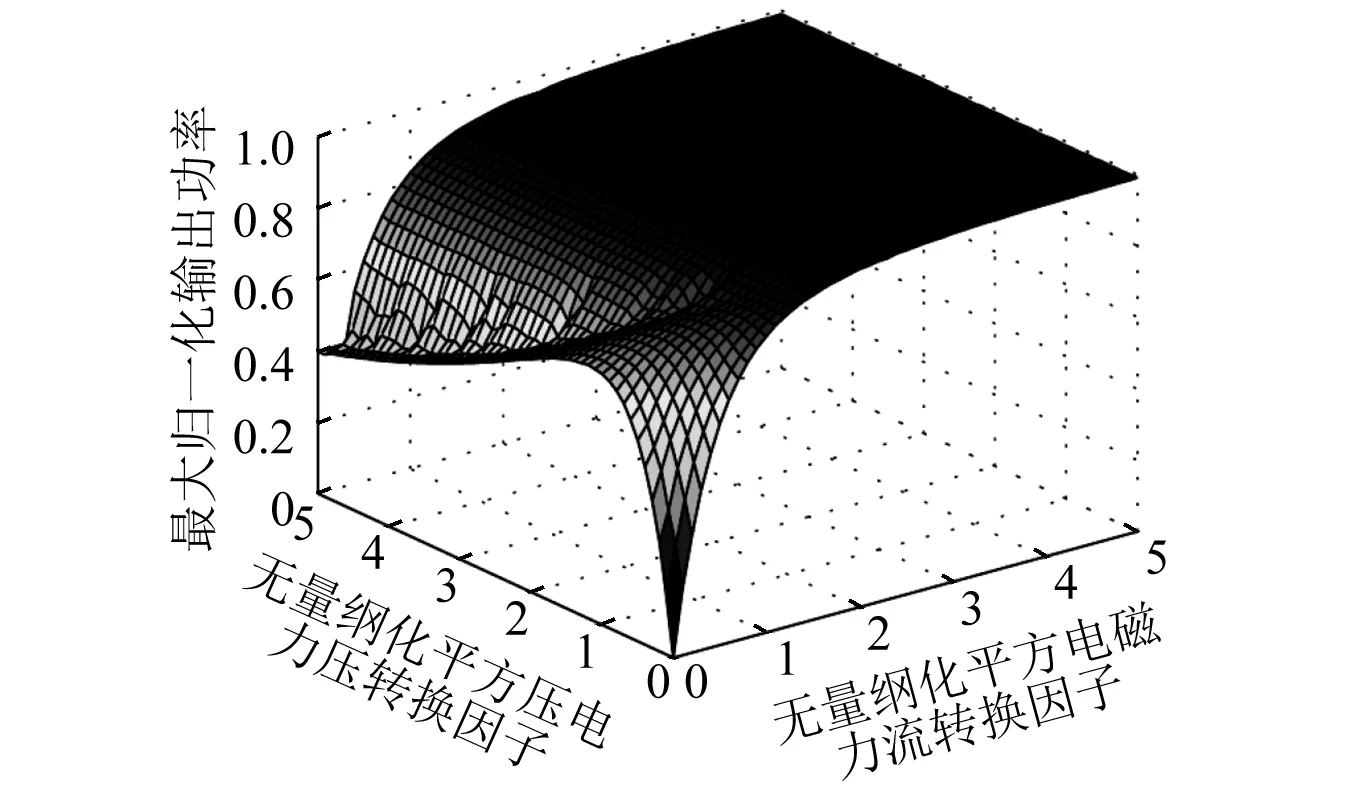
图6 共振时，最大归一化输出功率随2和2值变化仿真曲线Fig.6 The theoretical maximum normalized power as a function of 2 and 2 at resonance frequency

3.2 实验验证

为了验证理论模型与遗传算法求解最大输出功率及最优负载的正确性，本文研制了一台单自由度悬臂梁式压电-电磁复合动能采集器，并搭建了实验平台，如图7所示。表2给出了压电-电磁复合动能采集器样机的几何设计尺寸与所采用的制造材料。表3给出了压电-电磁复合动能采集器样机的相关物理参数。

图7 实验平台Fig.7 Experimental setup表2 压电-电磁复合动能采集器的几何参数与材料参数Tab.2 The geometrical and material parameters of the piezoelectric-electromagnetic hybrid vibration energy harvester

参数数值梁材料铍青铜梁尺寸85mm×16mm×0.5mm压电片材料PZT-5H压电片尺寸44mm×7.2mm×0.25mm压电常数d31/(pC·N-1)-274压电片数量1永磁体材料钕铁硼永磁体尺寸10mm×10mm×10mm剩磁强度/T1.009永磁体数量8线圈尺寸/mm3D20-d4×H10线圈匝数/匝500线圈数量1

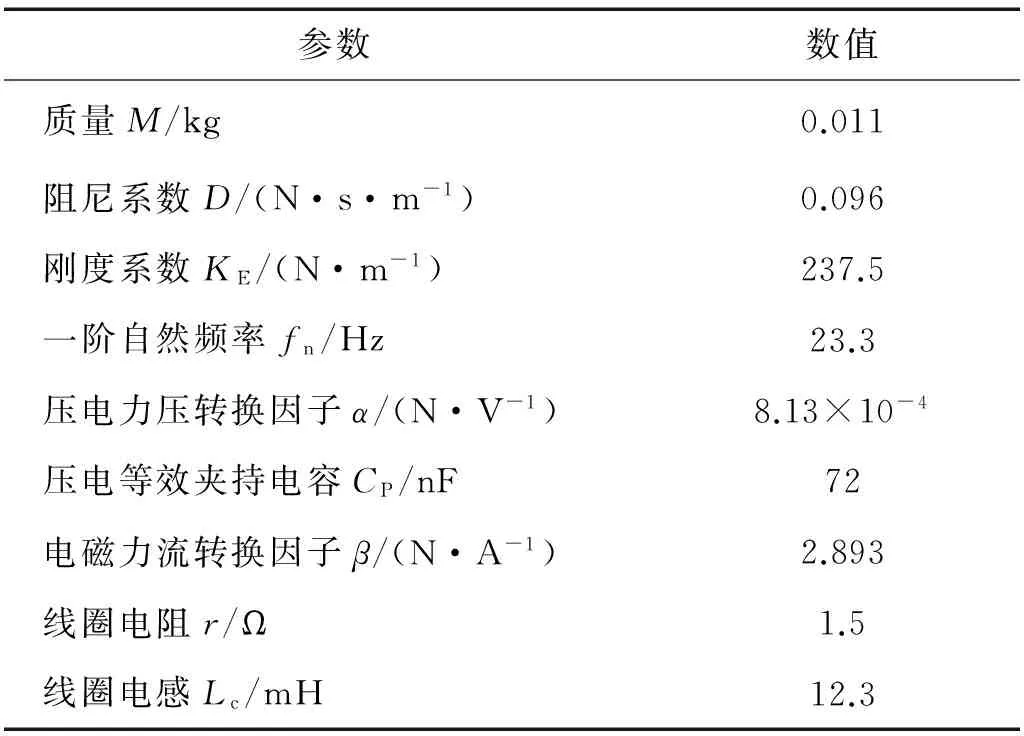
表3 压电-电磁复合动能采集器的物理参数Tab.3 The experimental parameters of the piezoelectric- electromagnetic hybrid vibration energy harvester

图8为采集器在基础激励加速度为0.5g时，其理论最大输出功率与实验最大输出功率随激励频率变化曲线。实验结果表明，实验曲线与理论曲线获得了较好的吻合，虽然在数值上存在一些差异，但仍处于可以接受范围内。当在激励频率在采集器的一阶共振频率点23.3 Hz时，最大输出功率的理论值与实验值分别为3.75 mW和3.42 mW，后者与前者相差8.8%。实验误差主要由以下几个因素引起：模型简化程度、遗传算法求解精度、实验样机制造精度等。

图9为采集器在基础激励加速度为0.5g和23.3 Hz时，其理论输出功率与实验输出功率随负载变化曲线。图9中的等高线表示理论值，而黑色标记符号则表示实验值。同一根等高线表示相同的理论输出功率值可以由不同的负载组合RP和RE获得，这事实上表明了压电-电磁复合动能采集器的优化负载范围与单一机电转换机制的压电或电磁动能采集器相比，获得了极大的扩展。利用本文提出的遗传算法进行采集器的最大输出功率与最优负载求解，得到其中一组最优负载组合RP=10 kΩ和RE= 100 Ω，该点对应的理论输出功率为3.75 mW，而实验输出功率值为3.42 mW，总误差仅有8.8%，这表明采用遗传算法获得的理论最优解在实验中具有较高的可行性。

图8 基础加速度为0.5g时，最大输出功率随频率 变化的仿真曲线和实验曲线Fig.8 The theoretical and experimental maximum power as a function of frequency under 0.5g acceleration

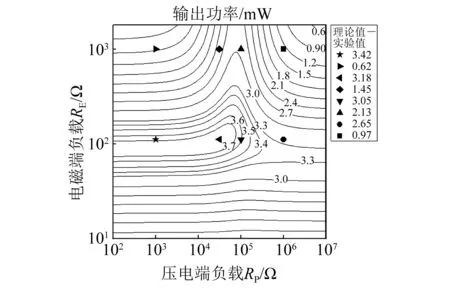
图9 基础加速度为0.5g和23.3 Hz时，输出功率随负载 变化的仿真曲线和实验曲线Fig.9 The theoretical and experimental power as a function of two loads under 0.5g and 23.3 Hz acceleration

4 结 论

本文建立了压电-电磁复合动能采集器的无量纲参数模型，并推导了采集器的归一化输出功率表达式；同时，提出了利用遗传算法快速求解采集器的最大输出功率及最优负载，并进行了数值仿真与分析，从而揭示了无量纲参数对采集器最大归一化输出功率的影响规律。最后，在理论推导的基础上进行了实验验证。综合理论与实验结果，得出以下结论：

(2)增大采集器的机械品质因子QM值，不会影响采集器的最大归一化输出功率，但是会减小其频率比宽度，即提高采集器频率选择能力；

(5)压电-电磁复合动能采集器最优负载范围比单一机电机制的压电或电磁动能采集器大的多。

下一步的研究工作是建立更加精确的压电-电磁复合动能采集器修正模型，进一步研究两种机电转换机制存在的耦合关系。

[1] POULIN G, SARRAUTE E, COSTA F. Generation of electrical energy for portable devices: Comparative study of an electromagnetic and a piezoelectric system[J]. Sensors and Actuators A: Physical, 2004,116(3):461-471.

[2] CHALLA V R, PRASAD M G, FISHER F T. A coupled piezoelectric-electromagnetic energy harvesting technique for achieving increased power output through damping matching[J]. Smart Materials and Structures, 2009, 18(9): 095029.

[3] SHAN X B, XU Z L, SONG R J, et al. A new mathematical model for a piezoelectric-electromagnetic hybrid energy harvester[J]. Ferroelectrics, 2013,450(1):57-65.

[4] WANG H Y, TANG L H, GUO Y, et al. A 2DOF hybrid energy harvester based on combined piezoelectric and electromagnetic conversion mechanisms[J]. A Journal of Zhejiang University Science, 2014,15(9):711-722.

[5] LI P, GAO S Q, NIU S H, et al. An analysis of the coupling effect for a hybrid piezoelectric and electromagnetic energy harvester[J]. Smart Materials and Structures, 2014,23(6): 065016.

[6] 蔡华通,高世桥,李平,等. 压电-电磁复合式俘能器的设计与实验研究[J]. 压电与声光, 2015,37(2):248-253.CAI Huatong, GAO Shiqiao, LI Ping, et al. Design and experimental study of hybrid piezoelectric and electromagnetic harvester[J]. Piezoelectrics and Acoustooptics, 2015, 37(2): 248-253.

[7] WILLIAMS C B, SHEARWOOD C, HARRADINE M A, et al. Development of an electromagnetic micro-generator[J]. Circuits, Devices and Systems, IEE Proceedings-. IET, 2001, 148(6): 337-342.

[8] GUYOMAR D, BADEL A, LEFEUVRE E, et al. Toward energy harvesting using active materials and conversion improvement by nonlinear processing[J]. IEEE Transactions on Ultrasonics Ferroelectrics & Frequency Control, 2005,52(4):584-595.

[9] WANG X, LIN L. Dimensionless optimization of piezoelectric vibration energy harvesters with different interface circuits[J]. Smart Materials and Structures, 2013, 22(8): 085011.

[10] HOLLAND J H. Adaptation in natural and artificial systems: an introductory analysis with applications to biology, control, and artificial intelligence[J]. The Quarterly Review of Biology, 1994, 69(1):126-137.

A study on the dimensionless parameter model of a piezoelectric-electromagnetic hybrid vibration energy harvester

XIA Huakang1, CHEN Renwen1, ZHU Liya2, REN Long1, ZHOU Qinbang1

(1.State Key Laboratory of Mechanics and Control of Mechanical Structures,Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China;2.Jiangsu Key Laboratory of 3D Printing Equipment and Manufacturing, Nanjing Normal University, Nanjing 210042, China)

In order to establish a unified performance comparison standard and obtain the maximum output power and the corresponding optimal loads for a piezoelectric-electromagnetic hybrid vibration energy harvester, a generalized dimensionless parameter model was introduced to address this problem. The expression of the theoretical normalized output power was derived, and the maximum value and the optimal loads were obtained based on a genetic algorithm; the relationships between the dimensionless parameters and the performance of the harvester were analyzed by numerical simulations, and the feasibility of the model and genetic algorithm for this topic were verified by an experiment. The results show: ① reducing coil resistance can improve the performance; ②improving mechanical quality factor can increase the frequency selectivity; ③ the performance is co-determined by piezoelectric and electromagnetic factors when the two effects are weak coupling, and the best performance is obtained at their matching point; ④ the performance is almost determined by the electromagnetic factor when it is strong coupling, and it increases to the ultimate performance with the electromagnetic effect; ⑤ the optimal load range is increased by using the piezoelectric-electromagnetic dual-coupling mechanisms.

energy harvesting; piezoelectric-electromagnetic; dimensionless parameter model; genetic algorithm

江苏省普通高校研究生科研创新计划(KYLX15_0247)；江苏省高校优势学科建设工程资助项目(PAPD)；江苏省高校自然科学研究面上项目(14KJB480004)

2015-11-03 修改稿收到日期： 2016-05-12

夏桦康 男，博士生，1989年生

陈仁文 男，教授，1966年生

E-mail:rwchen@nuaa.edu.cn

TN384；TM619

A

10.13465/j.cnki.jvs.2017.12.021