一种Stewart隔振平台的动力学建模及实验研究

谢溪凌， 王超新， 陈燕毫， 张志谊

(1. 上海交通大学 振动、冲击、噪声研究所， 上海 200240；2. 上海交通大学 机械系统与振动国家重点实验室， 上海 200240)

一种Stewart隔振平台的动力学建模及实验研究

谢溪凌1,2， 王超新1,2， 陈燕毫1,2， 张志谊1,2

(1. 上海交通大学 振动、冲击、噪声研究所， 上海 200240；2. 上海交通大学 机械系统与振动国家重点实验室， 上海 200240)

提出一种采用石墨自润滑球铰连接的立方体构型Stewart隔振平台，6个支腿通过可转动的球铰与基础及载荷平台相连，每个支腿由音圈作动器与力传感器构成。在假设各支腿、基础及载荷平台均为弹性体的基础上，采用子结构频响函数综合法对Stewart隔振平台进行动力学建模，并通过FEM方法进行验证，给出内嵌反馈控制的隔振平台模型，对反馈控制效果进行仿真验证；在仿真分析的基础上，对隔振平台的被动隔振性能和内嵌反馈控制的主动隔振性能进行实验。结果表明，被动隔振在30～200 Hz频段内具有约-36 dB/dec的衰减率，主动隔振在3～100 Hz频段内可获得最大20 dB的幅值衰减，<200 Hz，支腿力RMS值控制后下降75%～80%。

Stewart平台；主动隔振；频响函数综合；子结构；球铰；音圈作动器

近年来，测绘、通信等技术的发展对星载设备的观测分辨率、指向精度以及稳定性等提出更高要求，卫星姿态振荡、星上回转部件引起的卫星平台微振动逐渐成为影响高敏感有效载荷性能的瓶颈[1-3]。因此，抑制微振动，减小其对有效载荷的影响至关重要。

六自由度Stewart平台因具有精度高、刚度大、负荷自重比高、运动平稳等特性，被国内外众多学者采纳，并用于主、被动隔振平台，隔离振源与星体结构，实现抑制微振动的目的[4]。在六自由度平台中，立方体构型Stewart平台的雅可比矩阵具有正交解耦性，从而能够简化位姿运动学关系、易于控制和保持各个支腿的一致性[5]。

在Stewart平台中，各支腿与载荷平台、基础平台之间的连接铰链至关重要，直接影响着整个平台的精度、可靠性以及可重复性。铰链的设计指标包括承载能力、线性度、持久性、可容纳角度以及刚度等[6]。目前，连接铰链主要有虎克铰、弹性铰与球铰，虎克铰的万向节与轴孔之间摩擦不可避免，易导致非线性；弹性铰质量轻，但变形较小，允许位移受到限制；而球铰可实现较大范围转动，承载能力强，但其缺点是材料与润滑方式较难选择，而且质量较大。因此，合适的连接铰链是关系到整个平台性能的重要环节。

另一方面，Stewart平台因并联机构的复杂性，其动力学模型通常是一个多自由度、多变量、高度非线性、多参数耦合的复杂系统[7]，寻找准确高效的动力学建模方法一直是研究Stewart平台的热点问题之一。Dasgupta等[8-9]采用Newton-Euler法建立了6-UPS和6-SPS型Stewart平台闭环动力学模型，该方法直观，但需要计算所有关节的约束力及力矩，故对一些不必要的关节进行计算就显得多余，同时该方法无法考虑各个构件的柔性。Lee等[10]采用Lagrange方法对柔性Stewart平台进行动力学建模，该方法系统性较强，但仅考虑了支腿的柔性作用，基础与载荷平台仍作刚性考虑。郭洪波[11]综合运用Newton-Euler法和Lagrange方法建立起考虑各作动器惯量影响的六自由度平台完整动力学模型，融合了这两种方法的优点，建立的动力学模型适应相关控制器的设计和分析。Wang等[12]分别采用虚功原理研究Stewart平台的动力学问题。Liu等[13]采用Kane方法建立了并联机器人的动力学模型。值得注意的是，以上研究在考虑Stewart平台动力学模型时未完全考虑到各个支腿、基础和载荷平台的柔性，而实际中各构件均为弹性体，振动特性复杂，用上述方法无法准确描述整个平台的振动与传递特性，进而无法准确指导隔振平台的设计以及之后的控制器设计与分析。

本文提出一种基于石墨自润滑球铰连接的立方体构型Stewart隔振平台，其支腿均以球铰结构与基础及载荷平台相连接，单个支腿由音圈作动器与力传感器构成。在考虑各个支腿、基础及载荷平台均为弹性体的基础上，采用子结构频响函数综合法对Stewart隔振平台进行动力学建模，并通过FEM(Finite Element Method)方法进行验证。该建模方法可考虑各构件的柔性，能有效描述整个隔振平台动力学输入输出特性及其振动特性。推导了基于内嵌反馈控制的隔振平台模型，对反馈效果进行仿真验证。最后，通过实验模型对隔振平台的被动、主动隔振性能进行实验验证。

1 Stewart隔振平台方案与结构设计

考虑到立方体构型的Stewart隔振平台具有雅可比矩阵正交解耦性，提出一种立方体构型的Stewart隔振平台。该隔振平台主要由基础平台、球铰结构、力传感器、音圈作动器以及载荷平台构成,如图1所示。

图1 Stewart隔振平台模型Fig.1 Stewart isolation platform model

隔振平台每个支腿由力传感器和音圈作动器构成，各支腿与基础平台、载荷平台均通过自润滑球铰连接。球铰采用石墨自润滑技术，在球头部位均匀镶嵌石墨块，使球铰具有自润滑功能。与油润滑相比，石墨润滑具有不挥发、在强辐射条件下具有热化学稳定性以及在极端温度下保持良好润滑性能和低摩擦力等性能。此外，平台支腿两端的球铰结构完全相同，可简化隔振平台设计，保证各支腿性能的一致性。

2 Stewart隔振平台动力学建模及有限元验证

2.1 隔振平台动力学建模

在假设各支腿、载荷及基础平台均为弹性体的基础上，采用基于频响函数的弹性子结构综合法[14]对Stewart隔振平台进行动力学建模。首先将整个系统划分为载荷平台、并联隔振装置和基础平台三个弹性子结构，然后对子结构分别进行分析，得到子结构频响函数，最后利用子结构在连接界面处的力平衡条件和位移协调关系对三个子结构的频响函数进行综合，得到整个隔振平台的频响函数或输入输出特性。隔振平台子结构的划分示意图,如图2所示。

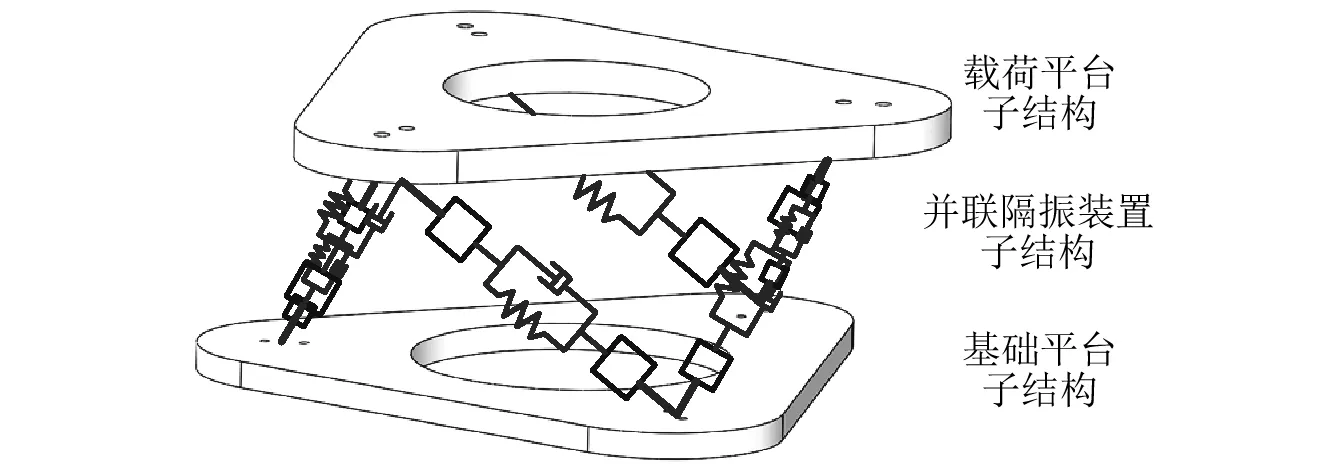
图2 隔振平台及其子结构Fig.2 Isolation platform and its substructure

对载荷平台(上标为P)和基础平台(上标为B)子结构分别进行建模，得出其频响函数分别可表示为：

(1)

式中：H为频响函数矩阵；x和f则为位移向量和节点受力向量；下标i为内点(一般为外激励点或感兴趣的响应点)；下标c为连接点。

根据式(1)可得整个系统综合前的频响函数矩阵：

(2)

现采用阻抗矩阵对载荷平台以及基础平台之间的弹性子结构(即并联隔振装置)进行描述，将各个支腿简化为由刚性杆、质量、弹簧、阻尼组成的结构，如图3所示。

图3 单个支腿的简化模型Fig.3 Simplified model of a single strut

集中质量的四端参数表达式为[15]：

(3)

(4)

式中：下标m1和m2分别为集中质量的相关力和位移；c1和c2分别为集中质量分配系数，即隔振装置单机中连接杆和质量块的质量在弹簧阻尼系统两端的分配比例。

由于集中质量与弹簧阻尼系统在轴向相连接，因此考虑隔振装置单机质量的四端参数模型可表示为：

(5)

式中：cV和kV分别为等效阻尼与等效刚度。由此阻抗矩阵可表示为：

(6)

综合前后，载荷平台和基础平台子结构在连接点处应该满足位移协调条件和受力平衡条件，由此可得：

(7)

将式(7)联立，可以得到综合前后力向量与位移向量之间的相互关系：

(8)

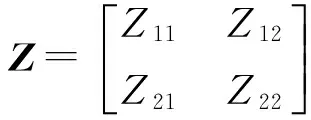
(9)

对于内点而言，其受力与位移在综合前后必保持一致，因此有：

(10)

综上，可得整体隔振平台的频响函数矩阵：

(11)

通过动力学建模推导出的整体隔振平台的频响函数，即可得出从激励点到响应点之间的输入输出特性。

2.2 建模方法有限元验证

在获得Stewart隔振平台整体频响函数后，建立Stewart隔振平台的有限元模型。模型中的基础平台与载荷平台均采用SHELL181单元，球铰结构采用MASS21单元，六个支腿采用MASS21和COMBIN14单元。六个支腿与基础平台及载荷平台的三个铰连接点采用球铰副模拟，具体操作方法为约束其平动自由度但释放其转动自由度。载荷平台质量为4.45 kg，基础平台质量为6.32 kg，各支腿等效刚度为3×104N/m。所建模型共划分3 009个单元，共1 103个节点。边界条件为：对基础平台底部三个均匀分布的点施加完全约束，载荷平台采用自由边界。通过FEM方法计算频响函数，计算频率范围0～500 Hz，步长为1 Hz。

在载荷平台的中心处分别施加三个方向(以垂直于载荷平台的方向为Z向)的单位激励力(1 N)，得到基础平台中心点处的频响曲线，如图4所示。

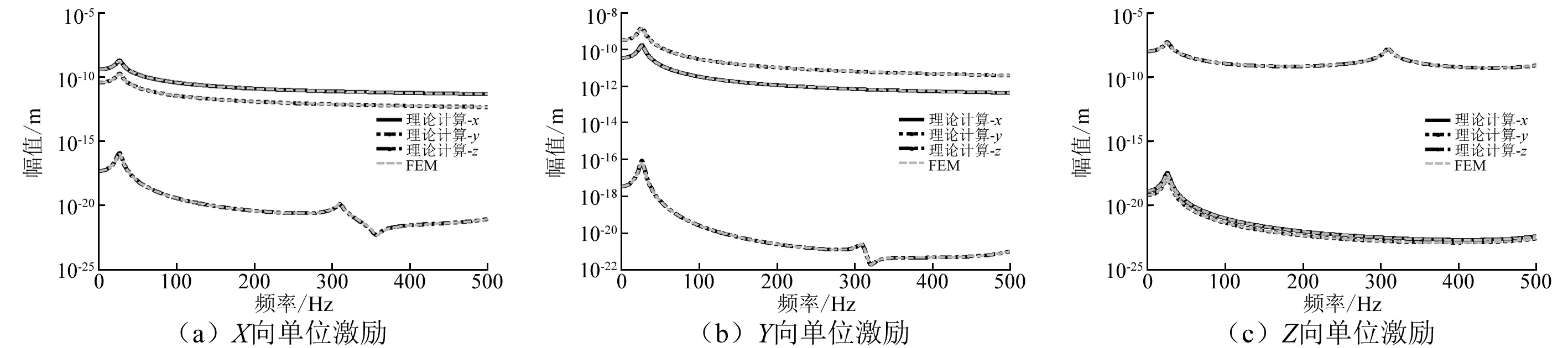
图4 基础平台中心点的幅频特性Fig.4 Magnitude-frequency curves of the center point of the base

由图4可知，通过弹性子结构频响函数综合方法计算出的频响曲线与有限元计算结果进行对比，在计算频段内数据与趋势吻合良好，表明此种建模方法有效，可以用于Stewart隔振平台的动力学特性研究以及控制器设计与分析。

3 Stewart隔振平台反馈控制分析

3.1 反馈控制系统建模推导

作为主被动一体隔振平台，其隔振效果与反馈控制系统设计密切相关。在对Stewart隔振平台进行动力学建模的基础上，建立以力为反馈信号的反馈系统[15]，并在此基础上推导出整个系统的动力学模型。反馈控制原理图，如图5所示。

图5 反馈控制原理Fig.5 Feedback control principle

在图5中，F1和x1分别代表载荷平台输出到支腿上的力和位移；F2和x2分别代表支腿输入到基础平台上的力和位移；cV、kV和mV1、mV2分别为音圈作动器的等效阻尼、等效刚度以及其两端的等效质量；kf为力传感器的等效刚度；F为力传感器检测到的力；h为反馈增益系数。

由此可得，反馈力Ff2构成的局部反馈的四端参数传递矩阵可表示为：

(12)

进而求得反馈后的基础-平台四端参数传递矩阵:

(13)

将式(13)转化为阻抗形式可得到：

(14)

式(14)即为单个支腿在力反馈情况下的轴向阻抗，将其扩展到六个支腿代入至上述动力学模型推导过程中的式(8)，最终可得在力反馈情况下综合后的整体隔振平台频响函数矩阵。

3.2 反馈效果分析

基于上述在内嵌反馈控制下的隔振平台模型，对反馈效果进行计算分析，分析中所用参数均与上述动力学模型参数一致。

反馈前后载荷平台中心激励到基础平台中心响应的频响曲线图，如图6所示。由图6可知，反馈效果明显，可以有效抑制共振峰处的振动，主共振峰(27 Hz)幅值得到明显抑制。

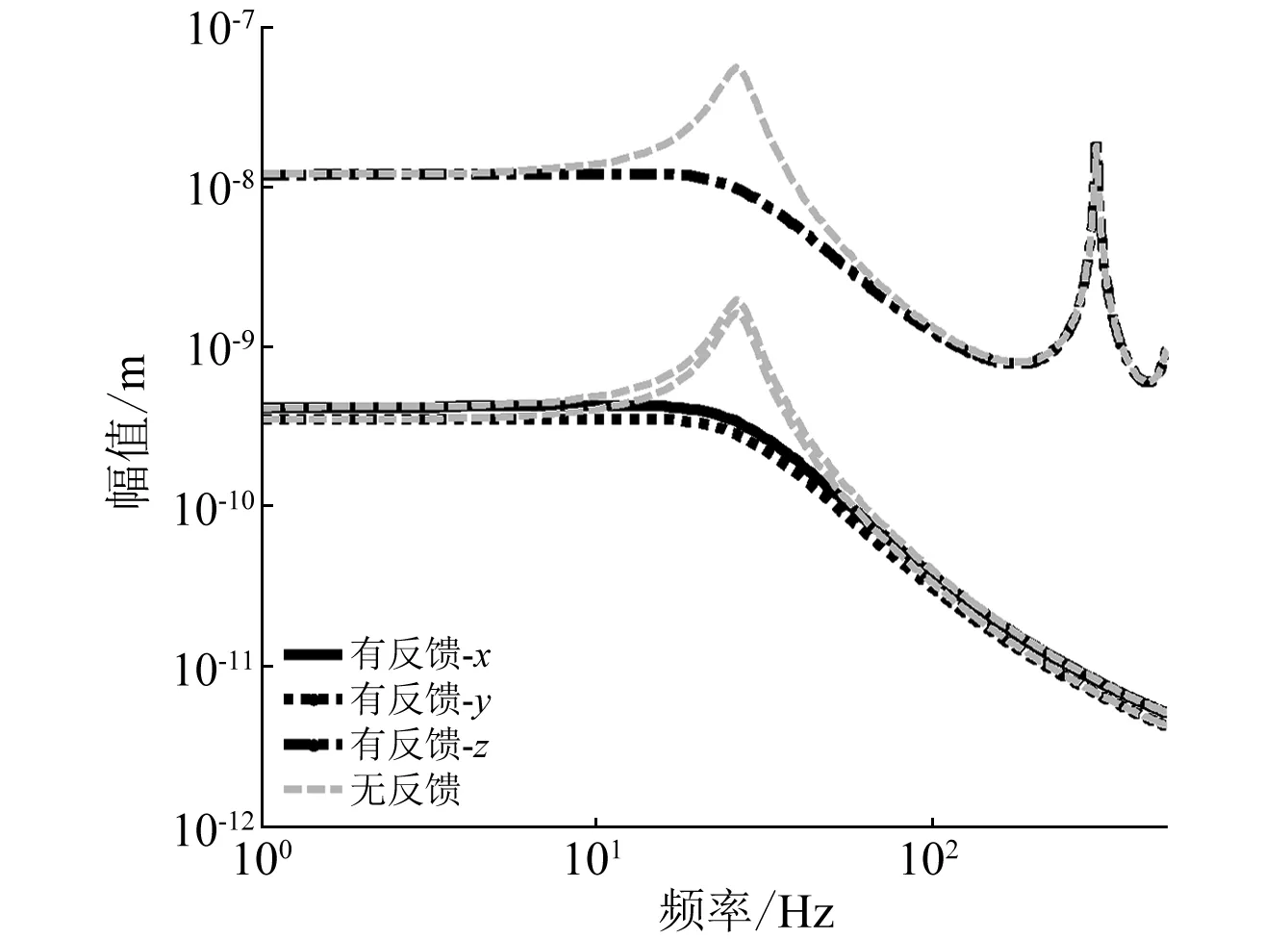
图6 反馈控制效果Fig.6 Effectiveness of feedback control

3.3 反馈稳定性分析

对单个支腿反馈控制系统(见图5)进行分析，xV1和xV2分别代表质量mV1和mV2的位移，其余参数含义与上述一致。

该系统运动微分方程可表示为：

(15)

由式(15)可得如下形式的频率方程：

mV1mV2s4+cV(mV1+mV2)s3+kV(mV1+mV2)s2+mV1kfhs=0

(16)

由式(16)可知，频率方程有一根为零，这是因为所分析系统的反馈回路中有一个积分环节，而实际力传感器的信号会通过内置高通滤波器的信号调理器进行处理，所以不会出现临界稳定的情况。

对于式(16)，根据Routh-Hurwitz准则，稳定的条件是全部系数为正且不等式(17)成立：

(17)

由此可得单腿反馈控制稳定的充要条件：

(18)

4 Stewart隔振平台被动隔振效果

4.1 被动隔振效果实验

对Stewart隔振平台的被动隔振效果进行实验研究，实验系统包括Stewart隔振平台、力锤、力传感器、信号调理器、功率放大器以及数据采集与分析仪等。通过锤击法进行测试，6个支腿上的力信号经由信号调理器调理，通过数据采集与分析仪接收，同时均以力锤的力信号为参考，取3次锤击的平均值作为结果，测得其传递特性和隔振效果，实验原理和隔振平台的实物，如图7所示。

图7 被动隔振实验和隔振平台实物Fig.7 Experiment of the passive isolation platform and its photograph

通过力锤沿Z向进行锤击，测得隔振平台从顶端到6个支腿力传感器的频响曲线，如图8所示。

图8 隔振平台被动隔振效果Fig.8 Passive isolation performance

4.2 主动隔振效果实验

在实验模型的基础上，搭建基于力反馈的控制系统，进行平台主动隔振效果实验。

对于一个反馈系统，稳定性是必要的[6]，因此在进行六支腿全反馈实验之前，首先考虑了单个支腿主动力与其余五个支腿主动力影响的比较。6个支腿工作时，1号支腿主动力与其余5个支腿主动力影响的对比,如图9所示。

图9 单个支腿主动力与其余五个支腿主动力影响的对比Fig.9 Comparison of influences between one active strut and other five active struts

由图9可知，在6个支腿同时工作时，1号支腿的驱动力相比于其余五个支腿串扰力的总和，在0～200 Hz频段内(共振峰处除外)，前者均比后者高出约5倍～35倍，而在共振峰处，两者相位相同，力的作用相互促进。因此，隔振平台在六个支腿全反馈时稳定。

隔振平台主被动隔振效果实验原理，如图10所示。与上述被动隔振性能实验不同的是，6个支腿上的力传感器信号在经过信号调理器调理后，有一路信号分支通过功率放大器输入到音圈作动器中，以此组成反馈回路。在反馈系统中，反馈参数的调节至关重要，实验中各支腿的反馈增益由力传感器对应的信号调理器来调节。

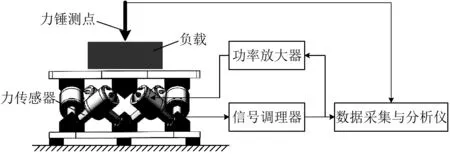
图10 主被动隔振效果实验原理Fig.10 Experiment of the passive/active isolation performance

图11分别为各个支腿上力反馈前后的频响曲线和时域响应。

由图11可知，六个支腿具有良好的一致性，共振峰出现在27 Hz附近，反馈可有效抑制共振峰处的振动，相比于控制前，共振峰下降约10 dB，在3～100 Hz频段内具有0～20 dB的衰减，同时时域响应也表明控制后效果明显。对比控制前后200 Hz内的RMS(Root Mean Square)值(见表1)可知，相比于控制前，控制后RMS值下降75%～80%。

图11 控制前后各支腿的频响曲线和时域响应Fig.11 Frequency response curves and time-domain responses of the struts before and after control表1 控制前后支腿力RMS值的比较Tab.1 Comparison of RMS values before and after control

支腿反馈前/N反馈后/N下降/%10.07840.018576.4020.06390.013179.5030.07210.015278.9240.07110.017175.9550.06800.013879.7160.08420.020775.42

5 结 论

本文提出一种采用石墨自润滑球铰连接的立方体构型Stewart隔振平台，在假设各支腿、基础及载荷平台均为弹性体的基础上，采用子结构频响函数综合法，建立Stewart隔振平台的动力学模型，得出隔振平台的频响函数，并通过FEM方法进行验证，结果表明动力学建模方法有效。给出了内嵌反馈控制系统模型，并进行仿真验证，仿真结果表明反馈控制可有效压制隔振平台共振峰处的振动。在仿真分析的基础上，对隔振平台的被动隔振性能和内嵌反馈控制的主动隔振性能进行实验，结果表明，被动隔振在30～200 Hz频段内具有-36 dB/dec的衰减率，主动隔振在3～100 Hz频段内可获得最大20 dB的幅值衰减，在200 Hz内，支腿力RMS值在控制后下降75%～80%。

[1] HUANG Xiuchang, SUN Jingya, HUA Hongxing, et al. Modeling and optimization of octostrut vibration isolation platform by FRF-based substructuring method[J]. Journal of Aerospace Engineering, 2015, 28(3): 04014084.

[2] PREUMONT A, HORODINCA M, ROMANESCU I, et al. A six-axis single-stage active vibration isolator based on Stewart platform[J]. Journal of Sound and Vibration, 2007, 300(3):644-661.

[3] SPANOS J, RAHMAN Z, BLACKWOOD G. A soft 6-axis active vibration isolator[C]// American Control Conference, Proceedings of the 1995. Seattle, WA: IEEE, 1995.

[4] THAYER D, CAMPBELL M, VAGNERS J. Six-axis vibration isolation system using soft actuators and multiple sensors[J]. Journal of Spacecraft and Rockets, 2002, 39(2): 206-212.

[5] ZHANG Yao, ZHANG Jingrui. Parameters design of vibration isolation platform for control moment gyroscopes[J]. Acta Astronautica, 2012, 81(2): 645-659.

[6] ERIC H A, MICHAEL F C, PAUL C J, et al. Precision, range, bandwidth and other tradeoffs in hexapods with application to large ground based telescopes[C]// Astronomical Telescopes and Instrumentation 2006: Technology Advancements. Orlando,FL, 2006.

[7] ANTONIO M L. Dynamic modeling of a Stewart platform using the generalized momentum approach[J]. Commun Nonlinear Sci Numer Simulat, 2009, 14(8): 3389-3401.

[8] DASGUPTA B, MRUTHYUNJAYA T S. A Newton-Euler formulation for the inverse dynamics of the Stewart platform manipulator[J]. Mechanism and Machine Theory, 1998, 33(8): 1135-1152.

[9] DASGUPTA B, MRUTHYUNJAYA T S. Closed-form dynamic equations of the general Stewart platform through Newton-Euler approach[J]. Mechanism and Machine Theory, 1998, 33(7): 993-1012.

[10] LEE J D, GENG Z. A dynamic model of a flexible Stewart platform[J]. Computers & Structures, 1993, 48(3): 367-374.

[11] 郭洪波. 液压驱动六自由度平台的动力学建模与控制[D]. 哈尔滨: 哈尔滨工业大学. 2006.

[12] WANG J G, GOSSELIN C M. A new approach for the dynamic analysis of parallel manipulators[J]. Multibody System Dynamics, 1998, 2: 317-334.

[13] LIU M J, LI C X, LI C N. Dynamics analysis of the gough-Stewart platform manipulator[J]. IEEE Transactions on Robotics and Automation, 2000, 16(1): 94-98.

[14] 傅志方, 华宏星. 模态分析理论与应用[M]. 上海: 上海交通大学出版社, 2000.

[15] 芮筱亭. 多体系统传递矩阵法及其应用[M]. 北京: 科学出版社, 2008.

[16] PREUMONT A, HORODINCA M, ROMANESCU I, et al. A six-axis single-stage active vibration isolator based on Stewart platform[J]. Journal of Sound and Vibration, 2007, 300(3): 644-661.

Dynamic modeling and experiment of a hybrid passive/active Stewart vibration isolation platform

XIE Xiling1,2, WANG Chaoxin1,2, CHEN Yanhao1,2, ZHANG Zhiyi1,2

(1. Institute of Vibration & Noise, Shanghai Jiao Tong University, Shanghai 200240, China;2. State Key Laboratory of Mechanical System and Vibration, Shanghai Jiao Tong University, Shanghai 200240, China)

A Stewart platform of cubic configuration was presented for hybrid passive/active vibration isolation. In the platform, the six struts are connected with the base and the payload through spherical joints lubricated by graphite, and each strut comprises a voice coil actuator and a force transducer. The Stewart platform was treated as an elastic system and an FRF (frequency response function) model was built by using the FRF-based substructure synthesis method. This model was validated by the finite element method and used in subsequent simulation. Vibration isolation with embedded feedback was analyzed and the effectiveness was evaluated. Experiments were also conducted to verify the hybrid passive/active vibration isolation performance. The results demonstrated that the passive isolation has approximately -36 dB/dec attenuation rate in the frequency range of 30-200 Hz, and the active isolation can achieve a maximum attenuation of 20 dB in the frequency range of 3-100 Hz. Moreover, the RMS values of dynamic forces in the struts were reduced by about 75%-80% within 200 Hz.

Stewart platform; active vibration isolation; frequency response function synthesis; substructure; spherical joint; voice coil actuator

国家自然科学基金(51275540)

2016-03-30 修改稿收到日期： 2016-05-09

谢溪凌 男，博士生，1994年生

张志谊 男，博士，教授，博士生导师，1970年生

TB535

A

10.13465/j.cnki.jvs.2017.12.033