一座异形斜拉桥的动力有限元模型与验证

李志刚，阳 霞，任伟新

(1.中交第二公路勘察设计研究院有限公司，武汉 430058； 2.合肥工业大学 土木与水利工程学院，合肥 230009)

一座异形斜拉桥的动力有限元模型与验证

李志刚1，阳 霞2，任伟新2

(1.中交第二公路勘察设计研究院有限公司，武汉 430058； 2.合肥工业大学 土木与水利工程学院，合肥 230009)

以一座异形钢结构人行桥为工程背景，探究了一种简洁有效的主梁模拟方法。给出了建立异形斜拉桥动力有限元模型的完整步骤；利用环境振动试验测试的模态结果，验证了所建模型的准确性和建模方法的有效性；运用有限元模型修正技术，对模型参数进行了分析和优化。结果表明该模型能较真实地反映实桥的动力特性，建模方法有很好的工程应用价值。

异形斜拉桥；有限元模型；环境振动试验；有限元模型修正

随着异形结构在桥梁工程中的使用程度日益频繁，桥梁结构分析的要求也不断提高。结构分析大多借助于有限元方法，精细模型虽比较准确但耗费较多资源，而工程应用需要的是有效且简单的有限元模型。目前异形斜拉桥的结构分析大多采用常规斜拉桥的简化方法，或者通过建立精细的模型以尽可能真实地模拟实桥，对于异形斜拉桥简单模型的建立并无过多的研究和参考。本文以一座异形斜拉桥为工程背景，运用通用有限元软件ANSYS，结合桥梁环境振动试验和有限元模型修正技术，就桥梁结构动力有限元模型的建立，进行一些研究和探讨。

1 工程简介

虹桥是常德市一座主梁线型呈“S”形的人行桥，平曲线半径160 m，宽5.5 m，跨径组合为(27 m+33 m+33 m+27 m)。主梁采用全焊接闭口钢箱梁截面，主梁标准断面，如图1所示。桥塔为高20 m的“帆”形钢塔，斜拉索在桥塔与主梁曲线内侧间呈空间“扇”形布置。主梁梁底除在中间墩一侧布置普通板式橡胶支座外，其余桥墩、桥台处布置双向滑动聚四氟乙烯板橡胶支座；主梁侧面在近桥塔侧布置起横向限位作用的单向滑动聚四氟乙烯板橡胶支座。虹桥总体布置，如图2所示。

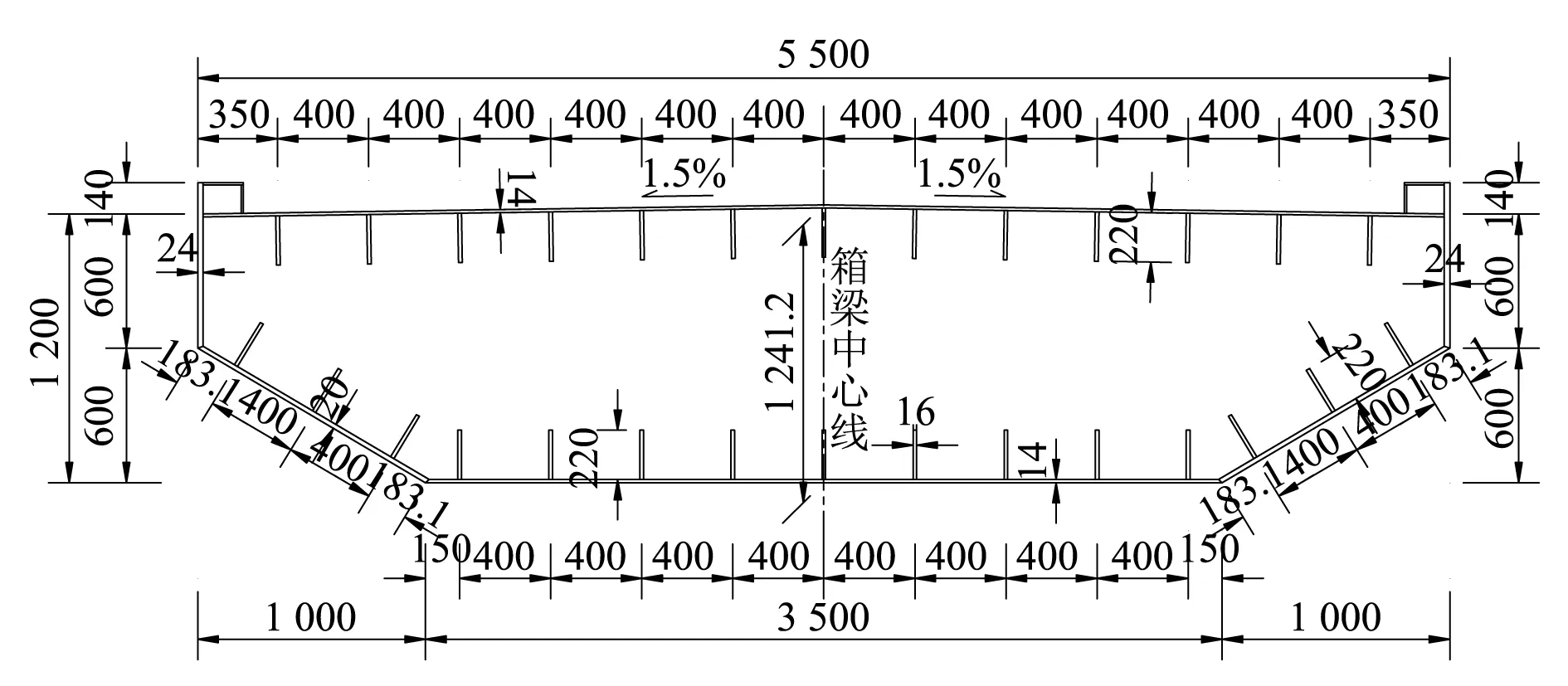
图1 主梁标准断面图Fig.1 Standard sectional view of the main beam

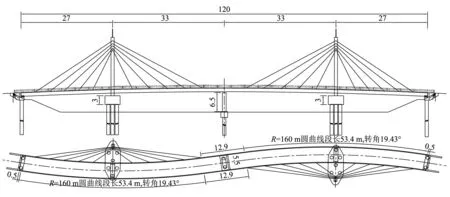
图2 虹桥总体布置Fig.2 The overall layout of the rainbow-bridge

2 有限元模型的建立

2.1 主梁建模方式的探讨

主梁的模拟是建模的重点，主梁模型的关键在于如何正确分配和等效桥面系的质量和刚度[1]。板壳单元虽然能较好地模拟空间曲线薄壁箱梁，但计算成本大；如果用分段的空间直线梁单元能实现准确地模拟，则可以大大提高结构分析的效率。为找到适合虹桥主梁建模的方法，在正式建模前，依照虹桥主梁的构造特征建立简支梁模型加以分析。简支梁截面同主梁标准断面，跨径取33 m，每3 m设置一个厚10 mm的横隔板。参考斜拉桥主梁的离散方式，简支梁模型分为以下几种：

模型1 脊梁模型[2]，采用beam4单元模拟中心主梁，取自由扭转惯性矩值作为扭转惯矩特性值；采用加在中心梁单元节点上的mass21单元模拟横隔板。中心梁两侧设置虚梁以便查看振型，中心梁与两侧虚梁用beam4单元刚臂联接。

模型2 脊梁模型，除中心梁扭转惯矩特性值取为等效扭转惯性矩Jeq[3]外，其余与模型1相同。

模型3 三主梁模型[4]，三个主梁均采用beam4单元模拟，其刚度和质量分配以及质量惯性矩等效见表1；横向联系采用约束方程模拟；横隔板的模拟同模型1。

模型4 脊梁模型，除中心梁采用考虑翘曲刚度(二次函数插值)的beam188单元模拟外，其余与模型1相同。

模型5 板壳模型，主梁采用shell93单元模拟，边界条件同以上各模型。

将各模型频率的计算值与理论值汇总于表2。由表2可知，模型4的弯曲频率误差较小，最大误差仅-2.17%，而模型1、模型2、模型3的弯曲频率误差较大，三阶竖

弯频率误差高达40%以上。可见对于这种高宽比(1/4.4)较大的闭口薄壁箱形截面梁，剪切变形对弯曲振动频率有较大影响。在扭转频率方面，模型1～模型4的计算误差均不大。可见对于这种截面的梁，仅考虑截面自由扭转刚度即可满足频率计算精度的要求。

由以上分析可知，模型4不论在计算弯曲频率还是在计算扭转频率方面，都能达到较理想的效果，可以把它作为虹桥主梁的基础建模方式。

表1 三主梁模型等效方式Tab.1 Equivalent way of the model with three main beams

2.2 有限元初始模型及模态分析

根据设计图纸，建立虹桥的有限元模型。主梁参照模型4的建模方式，中心主梁采用考虑翘曲刚度(二次函数插值)的beam188单元模拟，横隔板用加在中心梁单元节点上的mass21单元模拟，刚臂与外边梁均采用beam4单元模拟。与模型4不同的是，两侧外边梁有质量，从而将栏杆与基座的质量分散到两边。桥塔与3#桥墩均采用beam4单元，拉索采用link10单元，锚箱采用mass21单元建立在拉索锚点。桥塔、桥墩、桥台底均作固结处理，支座均采用combin14弹簧单元模拟。支座刚度值按照行业标准[5]计算，其它材料参数按相关规范[6-8]取值。全桥空间梁单元有限元模型，如图3所示。

表2 简支梁模型计算结果Tab.2 Results of simply supported beam models

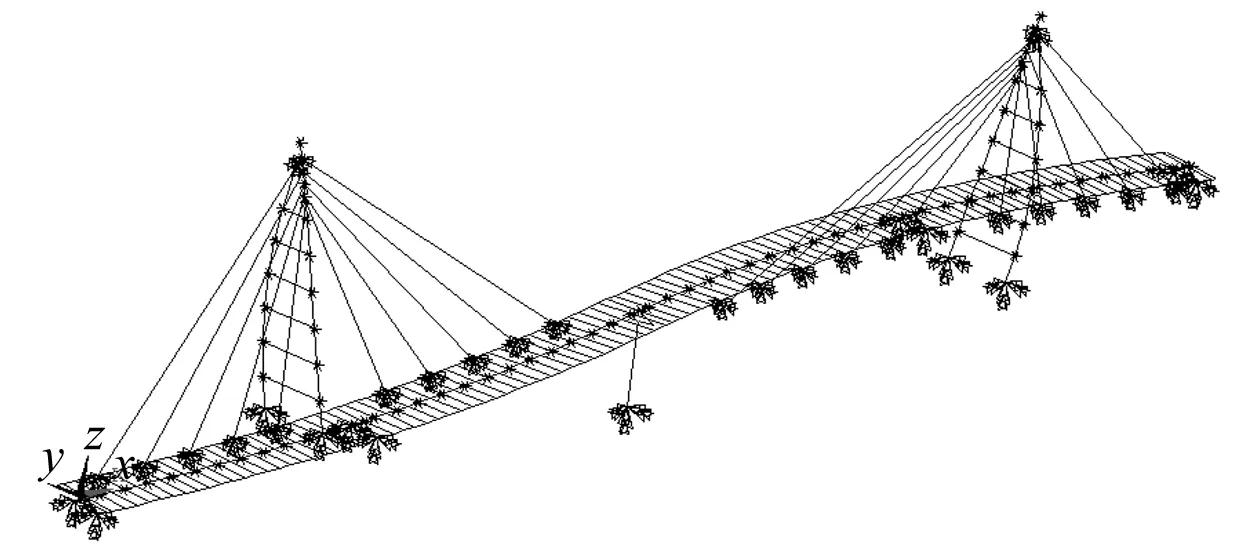
图3 虹桥梁单元有限元模型Fig.3 The finite element model with beam element of the rainbow-bridge

模态分析采用一致质量矩阵，模态提取采用分块兰索斯法，计算得虹桥主梁前几阶平弯、竖弯、扭转频率和振型形状，如图4～图10所示。

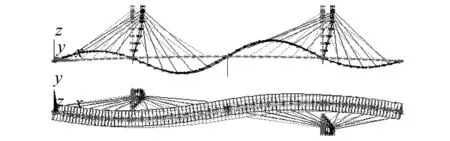
图4 主梁一阶竖弯，3.730 HzFig.4 The first vertical bending mode, 3.730 Hz

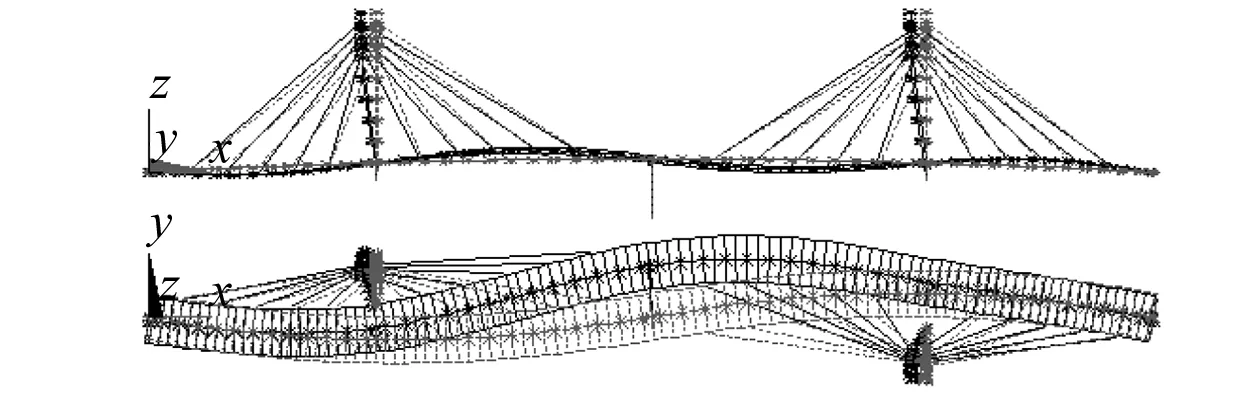
图5 主梁一阶平弯，3.745 HzFig.5 The first horizontal bending mode, 3.745 Hz

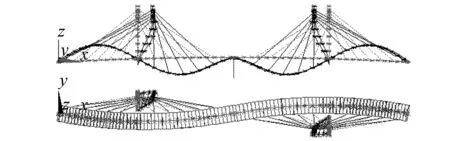
图6 主梁二阶竖弯，4.653 HzFig.6 The second vertical bending mode, 4.653 Hz

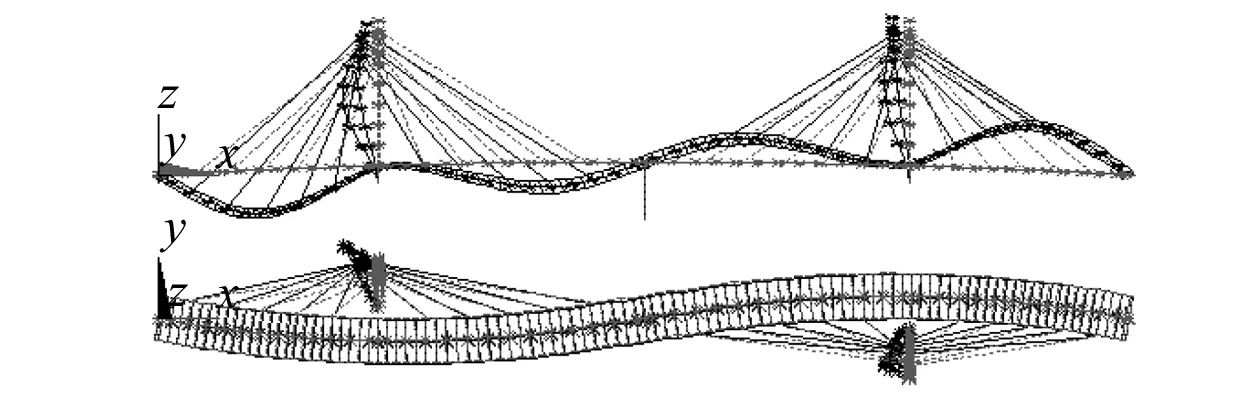
图7 主梁三阶竖弯，6.251 HzFig.7 The third vertical bending mode, 6.251 Hz

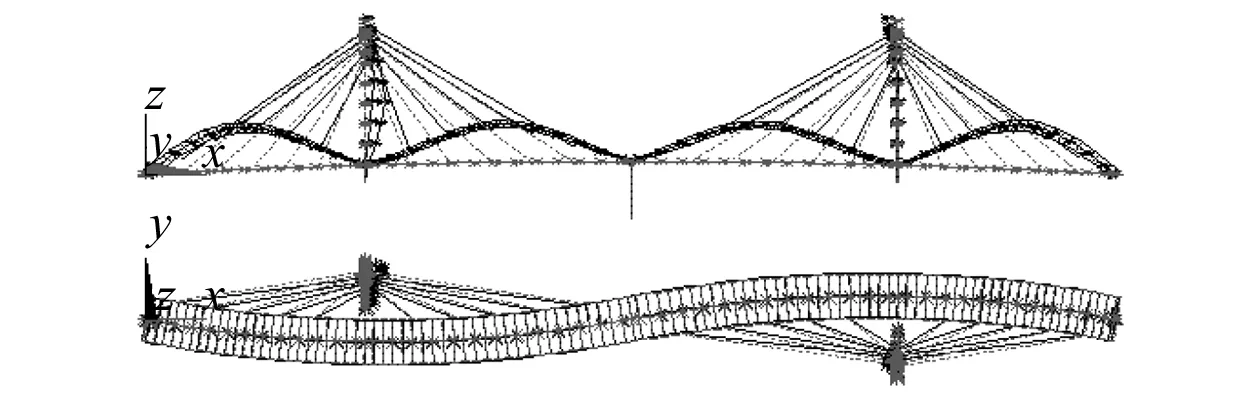
图8 主梁四阶竖弯，6.758 Hz Fig.8 The fourth vertical bending mode, 6.758 Hz

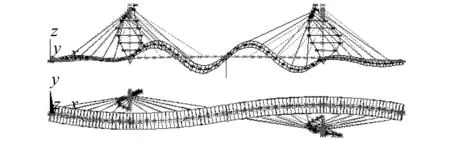
图9 主梁五阶竖弯，12.342 HzFig.9 The fifth vertical bending mode, 12.342 Hz

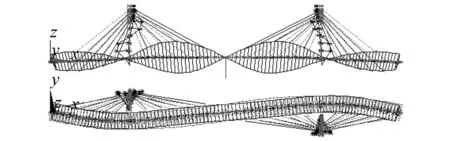
图10 主梁一阶扭转，18.227 HzFig.10 The first torsion mode, 18.227 Hz

3 有限元模型的试验验证

3.1 现场环境振动试验及模态识别

为验证有限元模型的准确性，对虹桥进行了环境振动试验。为测得主梁的竖向、横向和扭转振型，桥面上布置了两排竖向测点和一排水平测点，测点位置分别对应各斜拉索以及桥墩、桥台，全桥共计75个测点，测点布置，如图11所示。现场测试时采样频率为500 Hz，采样时间为15 min。数据处理时重采样频率采用50 Hz，采用汉宁窗加窗，窗口长度为1 024个点。分别采用数据驱动随机子空间方法[9]和峰值法[10]进行模态参数识别，并将识别出的参数对比校核，最终得到试验模态分析结果，如图12～图18所示。

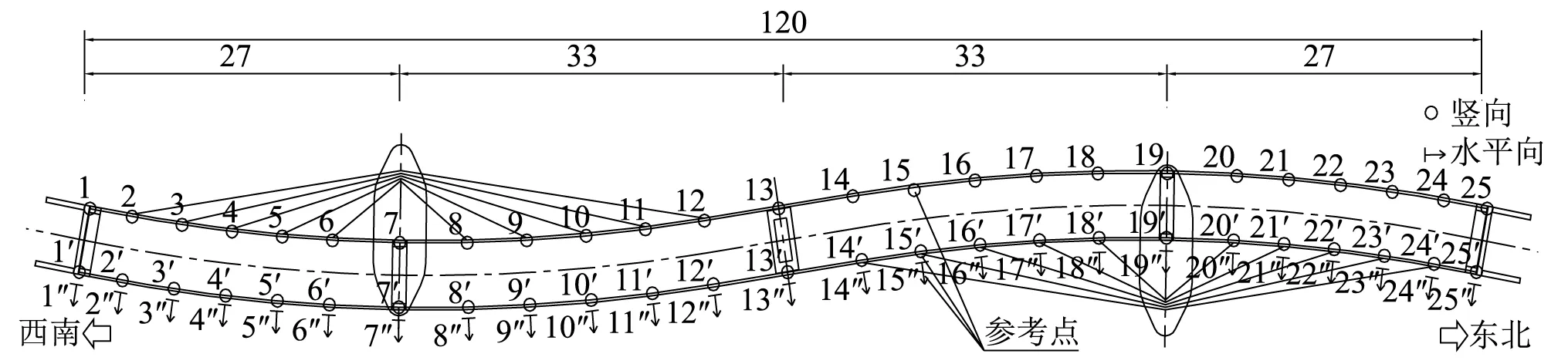
图11 测点布置图 Fig.11 The arrangement of measuring points

图12 一阶平弯振型，频率3.310 Hz Fig.12 The first horizontal bending mode, 3.310 Hz

图13 一阶竖弯振型，频率3.782 HzFig.13 The first vertical bending mode, 3.782 Hz

图14 二阶竖弯振型，频率4.700 HzFig.14 The second vertical bending mode, 4.700 Hz

图15 三阶竖弯振型，频率6.056 HzFig.15 The third vertical bending mode, 6.056 Hz

图16 四阶竖弯振型，频率6.506 HzFig.16 The fourth vertical bending mode, 6.506 Hz

图17 五阶竖弯振型，频率12.027 HzFig.17 The fifth vertical bending mode, 12.027 Hz

图18 一阶扭转振型，频率17.322 HzFig.18 The first torsion mode, 17.322 Hz

3.2 初始有限元模型的验证

为定量评定有限元模型的准确性，分别考察模型计算结果与试验测试结果间的频率相关性和振型相关性。频率相关性Eω表达式为：

(1)

式中：ωt为试验测试频率；ωa为有限元计算频率；振型相关性则采用模态保证准则MAC(ModalAssuranceCriterion)[11]计算：

(2)

式中：φt和φa分别表示测试的和有限元计算的振型向量。计算结果见表3。

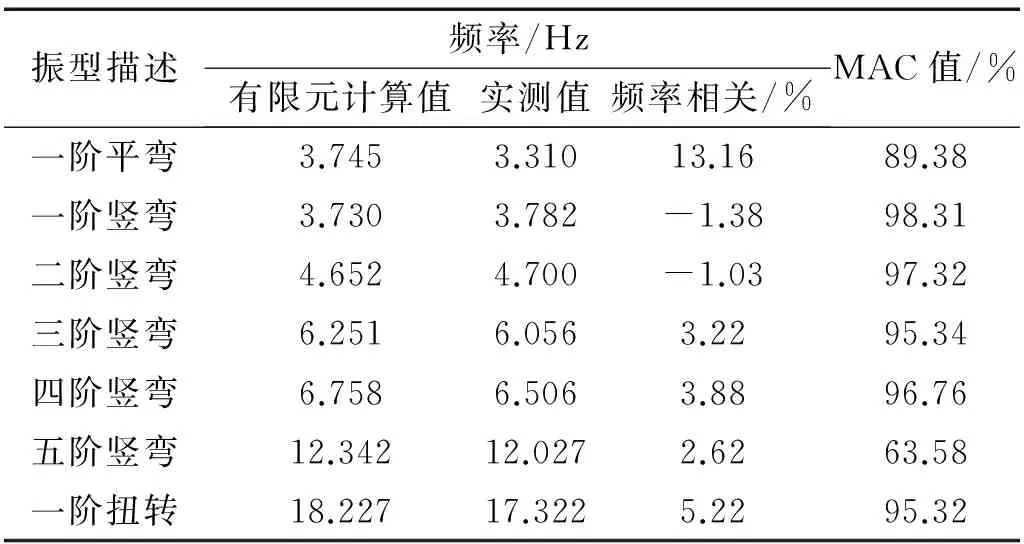
表3 初始模型频率相关性和振型相关性Tab.3 Eω and MAC of the initial model

由表3可知，在频率相关性方面，除一阶平弯频率差值达到13.16%外，其余各阶频率差值均在5%左右，相关性较好；在振型相关性方面，除五阶竖弯MAC值为63.58%外，其余各阶的MAC值基本达到90%以上，相关性很好。即虹桥的动力有限元模型能较好的模拟结构的真实状态，为一个比较理想的结构动力分析基础模型，但在计算平弯振动方面有待进一步优化。

4 有限元模型修正

4.1 模型参数优化

为探究初始模型误差的根源，进一步提高模型的精度，运用有限元模型修正技术对虹桥的初始模型进行参数优化，进而指导精确有限元模型的建立。修正时，通过经验和参数灵敏度分析，如图19所示。选取主梁的弹性模量和密度、主塔的弹性模量、栏杆与基座线密度、锚箱质量、边墩支座(GYZF4d400×71)的受压刚度、桥台支座(GYZF4d250×65)的受压刚度、横向限位支座(GJZF4150×150×44)的受压刚度等共8个参数作为待修正的参数；各参数初始值和修正变化范围，如表4所示。

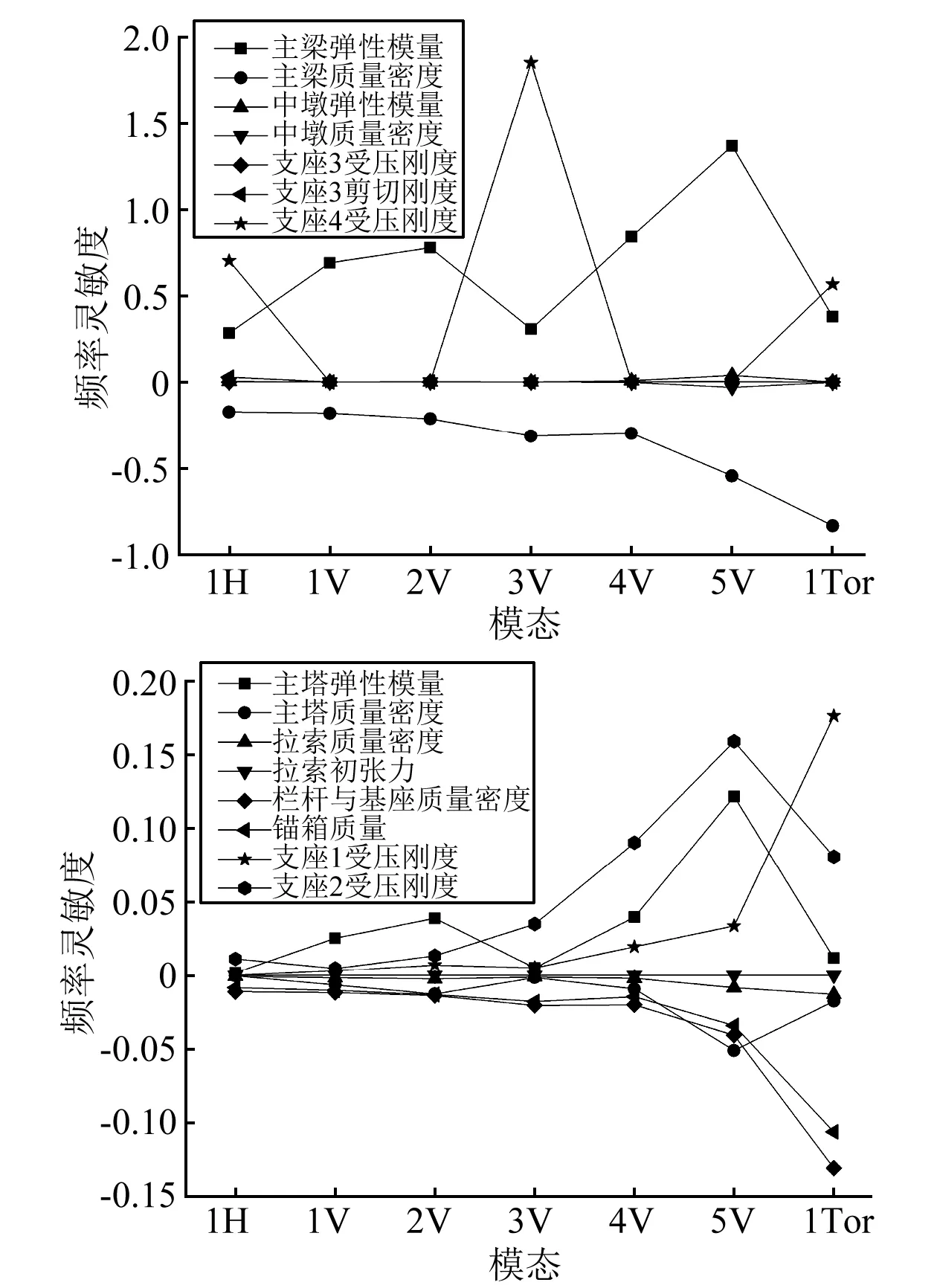
图19 灵敏度分析曲线Fig.19 Sensitivity analysis curve

通过联合频率残差和振型残差[12]建立模型修正的目标函数，表达式如下：

(3)

式中：λ=(2πf)2，f为自然频率，λaj与λtj分别对应有限元模型和试验模型；mf为试验所识别的频率数量；MAC为式(2)中的模态保证准则；ms为试验所识别的振型数量。

表4 修正参数初始值与变化范围Tab.4 Initial value and variation range of parameters

在进行优化计算时，首先采用随机搜索的方法获得多个合理的序列，然后以其中最好的序列为基础序列，使用子问题逼近法优化获得关于全局的优化序列，接着使用一阶优化方法对子问题逼近法的优化结果做进一步的细化，多次重复这一优化过程，直至优化结果稳定、满足要求。在优化迭代的过程中，通过计算MAC值的来确保各阶振型相互匹配，同时结合参数的灵敏度分析对修正参数进行适时调整。修正后的有限元模型与试验模型的频率相关性和振型相关性如表5所示，修正前后的参数变化，如表6所示。

4.2 修正参数的分析

由表5可知，修正后有限元模型的各阶频率与实测频率吻合得很好，误差最大不超过3%，特别是一阶平弯与一阶扭转频率吻合程度提高了很多；各阶振型MAC值均较大，修正后有限元模型的各阶振型与实测振型依然吻合很好。

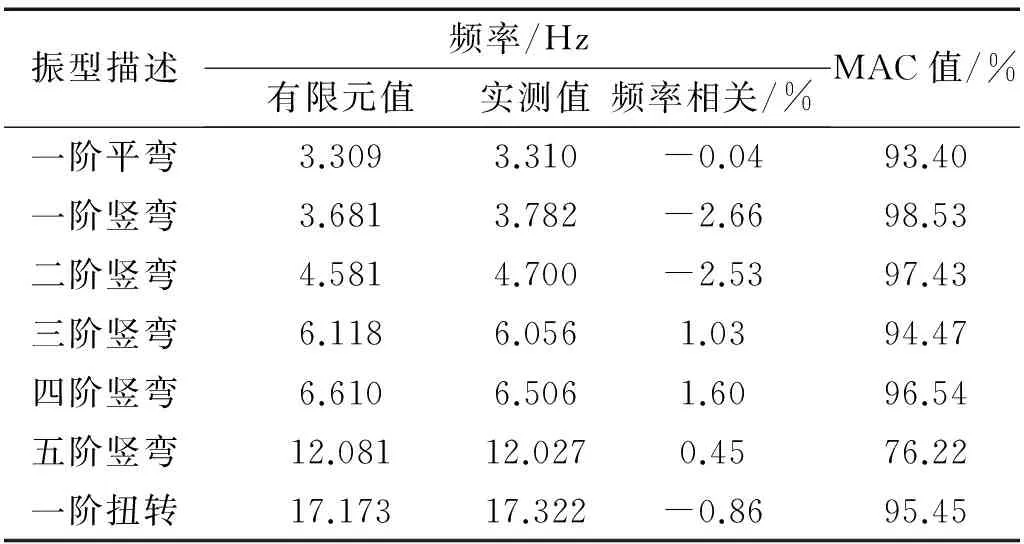
表5 修正后的有限元模型频率相关性和振型相关性Tab.5 Eω and MAC of the modified model

由表6可知，支座刚度、锚箱质量以及栏杆与基座线密度变化较大，主梁弹性模量与密度、主塔弹性模量等值略有增加。分析其原因：①焊接不锈钢栏杆实际会增大主梁刚度；②主梁附加的管线及未计入的细部构件会增加主梁质量；③桥塔较密的局部加强构件会导致主塔整体刚度的增大；④初始模型未计入拉索锚头的质量；⑤栏杆与基座质量由于加工的原因难以准确计量；⑥橡胶支座刚度值比较离散，虹桥结构容易造成支座偏压而使得支座实际受压刚度下降。

表6 修正后各参数的变化Tab.6 Variation of parameters after updating

由以上分析可得以下结论：①虹桥的体量不大，附属构件对其动力特性有较大影响；②将栏杆与基座的质量分散到两边虚梁上的做法比较合理，且应一并计入其它附加质量；③建模时拉索锚点应将锚头的质量计入；④橡胶支座的刚度参数比较离散，初始建模时难以准确把握。

4.3 模态分析结果比较

用shell93板壳单元模拟主梁，其余均与初始模型相同，建立有限元模型，如图20所示。计算其自振频率，并将各模型的频率计算结果整理列入表7。

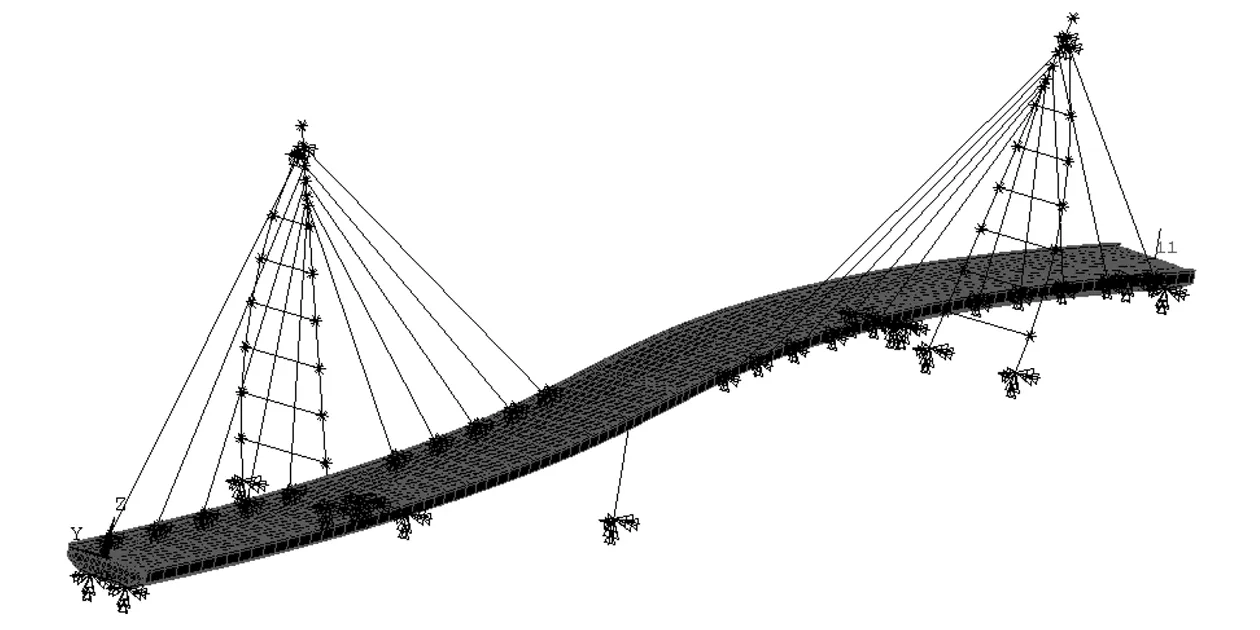
图20 虹桥板壳单元有限元模型Fig.20 The finite element model with shell element of the rainbow-bridge

从表7中各模型的计算结果可知，板壳模型的精确度略高于初始模型，但低于修正后的模型，进一步佐证了上文简化模型的准确有效。

5 结 论

(1)与试验模型和板壳模型的对比表明，本文建立的简化有限元模型能比较准确地模拟虹桥这种异形结构桥梁。

(2)不确定结构的建模方法时，可通过分析简单模型的途径找到结构的基础建模方法。

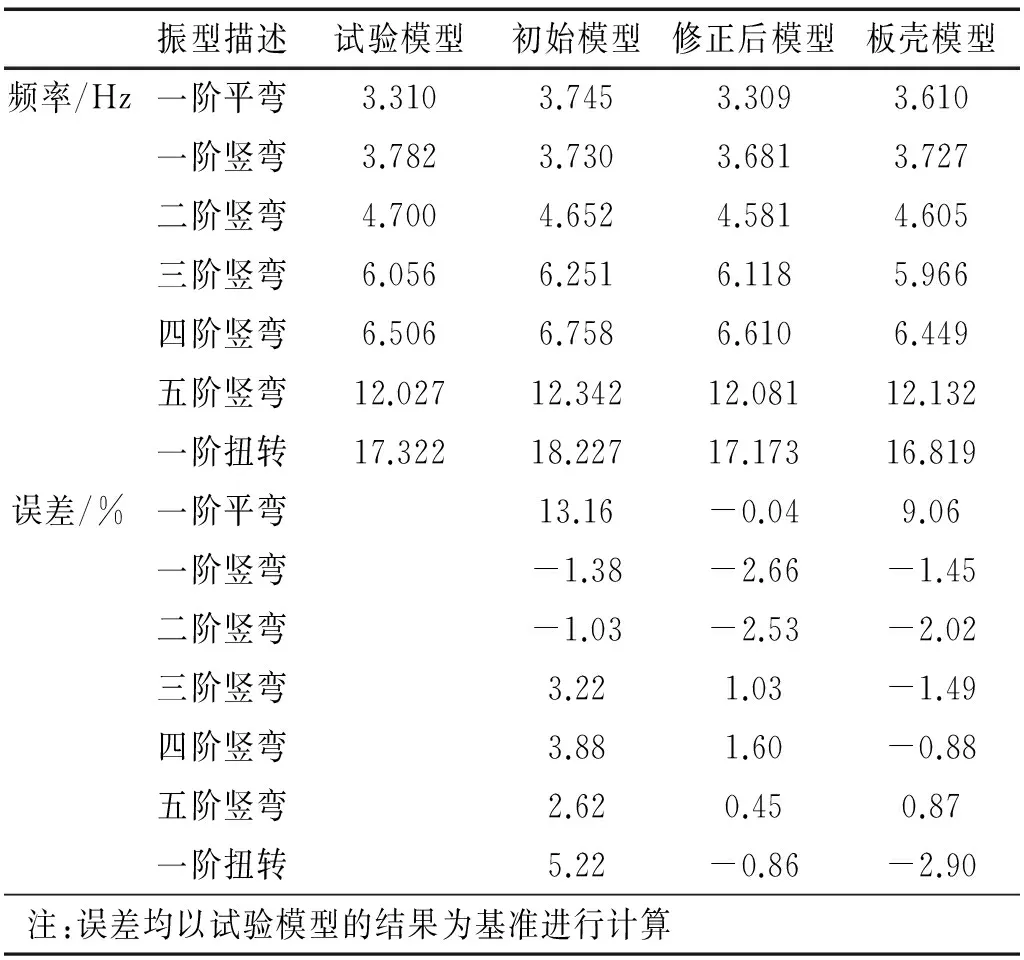
表7 各模型的频率计算结果Tab.7 Results of frequency calculation of models

(3)“高宽比”较大的闭口薄壁箱梁，截面剪切变形对其自振频率的影响大，计算时应考虑剪切变形的影响；同时，由于其截面自由扭转刚度较大，仅考虑自由扭转刚度即可满足频率计算精度要求。

(4)虹桥的现场环境振动测试试验表明，基于环境激励的振动试验不仅方便、快捷，还能较好的用于识别刚度较大、频率较高桥梁的模态参数。

(5)对于体量较小的钢结构人行桥，小构件对于有限元模型的精度也能产生较大影响，利用有限元模型修正技术，可有效地提高有限元模型的精度。

[1] 任伟新, 彭雪林. 青洲斜拉桥的基准动力有限元模型 [J]. 计算力学学报, 2007, 24(5): 609-614. REN Weixin, PENG Xuelin. Baseline dynamic finite element model of Qingzhou cable-stayed bridge [J]. Chinese Journal of Computational Mechanics, 2007, 24(5): 609-614.

[2] 范立础. 桥梁抗震 [M]. 上海: 同济大学出版社, 1997.

[3] WILSON J C, GRAVELLE W. Modeling of a cable-stayed bridge for dynamic analysis [J]. Earthquake Engineering and Structural Dynamics, 1991, 20(8): 707-721.

[4] ZHU L D, XIANG H F, XU Y L. Triple-girder model for modal analysis of cable-stayed bridges with warping effect [J]. Engineering Structures, 2000, 22(10), 1313-1323.

[5] 公路桥梁板式橡胶支座规格系列 : JT/T 663—2006[S]. 北京: 人民交通出版社, 2004.

[6] 钢结构设计规范:GB 50017—2003 [S]. 北京: 中国计划出版社, 2003.

[7] 公路钢筋混凝土及预应力混凝土桥涵设计规范: JTG D62—2004 [S]. 北京: 人民交通出版社, 2004.

[8] 公路桥涵通用设计规范:JTG D60—2004[S]. 北京: 人民交通出版社, 2004.

[9] 任伟新. 环境振动系统识别方法的比较分析 [J]. 福州大学学报(自然科学版), 2001, 29(6): 80-86. REN Weixin. Comparison of system identification methods using ambient vibration measurements [J]. Journal of Fuzhou University (Natural Science), 2001, 29(6): 80-86.

[10] REN W X, OBATA M. Elastic-plastic seismic behavior of long span cable-stayed bridges [J]. Journal of Bridge Engineering,1999, 4(3): 194-203.

[11] BROWNJOHN J M W, MOYO P, OMENZETTER P, et al. Assessment of highway bridge upgrading by dynamic testing and finite-element model updating [J]. Journal of Bridge Engineering, 2003, 8(3): 162-172.

[12] JAISHI B. Finite element model updating of civil engineering structures under operational conditions [D]. Fuzhou: Fuzhou University, 2005.

Dynamic finite element model and validation of a special-shaped cable-stayed bridge

LI Zhigang1, YANG Xia2, REN Weixin2

(1.CCCC Second Highway Consultants Co. Ltd., Wuhan 430058, China;2. School of Civil Engineering, Hefei University of Technology, Hefei 230009, China)

Based on a special-shaped steel pedestrian bridge, the finite models of girder were discussed. A concise and effective model of the special-shaped cable-stayed bridge was established and the procedure of finite element modeling was presented. The effectiveness of the finite element model of the bridge was verified by an ambient vibration test. By use of the finite element model updating method, parameters of the finite element model were analyzed and optimized. Result shows that the finite element model can reflect the bridge in dynamic characteristics accurately. The modeling method is useful in bridge engineering application.

special-shaped cable-stayed bridge; finite element model; ambient vibration test; finite element model updating

国家青年科学基金项目(51308175)

2016-02-19 修改稿收到日期： 2016-05-30

李志刚 男，硕士，工程师，1984年生

阳霞 女，博士生,1986年生

E-mail:yangx@mail.hfut.edu.cn

U44

A

10.13465/j.cnki.jvs.2017.12.010