飞艇主气囊结构湿模态分析与试验研究

邱振宇，陈务军，赵 兵，高成军，余征跃

(上海交通大学 空间结构研究中心，上海 200240)

飞艇主气囊结构湿模态分析与试验研究

邱振宇，陈务军，赵 兵，高成军，余征跃

(上海交通大学 空间结构研究中心，上海 200240)

为研究飞艇主气囊结构模态特性，将飞艇内、外气体假设为势流体，基于流固耦合理论和势流理论，建立薄膜与内外空气流场共同作用的理论模型。建立充气膜结构数值分析方法，在内、外流场的单面耦合和内、外流场的双面耦合三种情况下，对薄膜充气管和模型飞艇进行湿模态分析，对比分析单面和双面气固耦合的分析结果，并通过模态试验对分析方法进行验证，结果表明采用双面耦合分析方法分析充气膜结构湿模态最合理；采用此方法对艇长5 m、25 m、50 m和100 m以及长细比为 1∶3、1∶3.5和1∶4的双轴椭球外形飞艇主气囊在多种内压条件下进行湿模态分析，表明固有频率与艇长成反比，而长细比与内压对固有频率影响小。分析结果可以为飞艇的结构设计以及复杂充气膜结构模态分析提供参考。

飞艇主气囊；模态分析；势流体；湿模态；流固耦合

主气囊是反映柔性飞艇特点的主体结构，其结构性能对飞艇整体性能具有重要的影响[1]。主气囊作为典型的充气膜结构，分析其自振特性必须考虑内外流场的耦合作用，即对结构进行湿模态分析。目前对充气膜结构进行湿模态分析的方法主要有附加质量法和气固耦合法。前者将空气随结构振动的影响作为附加质量添加到主体结构中，附加质量的大小与结构自身的形状、模态振型和空气密度有关；后者基于势流理论，将空气作为势流体引入模态分析，通过界面边界协调条件使结构边界节点与流体边界节点的耦合，求解结构的气固耦合模态。

计算膜结构空气附加质量的方法主要有行波理论、细长翼理论和薄翼理论，为平面薄膜的空气附加质量计算提供了依据。利用理论公式计算附加质量，要求结构形状规则。王基盛等[2-3]推导了规则几何外形实体的附加质量计算公式。毛国栋等[4]推导了封闭式薄膜和开敞式薄膜的附加质量计算公式；高海健等[5-6]采用拟密度法导入薄膜附加质量，通过数值方法分析了薄膜充气管和飞艇的干湿模态；Li等[7-8]应用薄翼理论和振型分区方法分析了平面圆形薄膜和三角形空间薄膜结构的模态特性。用附加质量法分析膜结构的模态特性，虽然较为准确地反映了流场对结构模态的影响，但未揭示流体与结构耦合作用的本质。并且由于各阶模态振型不同，其附加质量也随之变化，要准确求解各阶振型对应的附加质量也存在困难。

采用气固耦合数值方法进行膜结构湿模态，可以对外形不规则的复杂膜结构耦合模态求解，联立流体方程和结构方程，建立统一的流固共同作用方程，更好地反映了流场对结构模态的影响。Epureanu等[9-10]通过理论推导给出了膜结构气固耦合的理论计算方法，并给出简单算例对理论进行阐述，但未给出具体数值分析方法；陈宇峰等[11]验证了薄膜预应力导入方式的合理性，通过ADINA分析平面薄膜的耦合模态，研究了空气对薄膜自振特性的影响。但并未给出复杂膜结构气固耦合数值求解方法。李鹏等[12]推导了内充气体与膜材共同作用的理论方法，并采用ADINA分析了薄膜充气管与内充气体的单面耦合模态；宋月萧等[13]以“水立方单元”为分析对象，在形态分析的基础上进行了气枕结构湿模态分析。在分析中均考虑了内充气体压力对结构刚度的贡献，并计入内充气体体积变化引起的内压变化，但忽略了结构外流场的作用，未对其单面耦合分析的合理性进行足够说明。

本文基于流固耦合理论和势流理论，将空气势流体引入薄膜充气结构模态分析中。建立充气结构内外流场理论模型和分析方法，采用单面耦合和双面耦合方法对薄膜充气管和飞艇模型进行湿模态分析，并分别与模型试验结果进行对比分析，验证了充气膜结构的湿模态分析方法。并对艇长5 m、25 m、50 m和100 m以及长细比为 1∶3、1∶3.5和1∶4的典型外形飞艇主气囊进行湿模态分析，研究了飞艇的模态特性。

1 充气膜结构模态分析理论模型

1.1 气体平衡方程

由于充气膜结构围绕平衡位置做自由振动时，对周围气体扰动较小，且气体处于静止无旋的初始状态，即可将充气膜周围气体假设为理想的势流体。

且由于充气膜结构外侧为具有无穷远边界条件开敞流场，在小扰动下，外流场气体可视为不可压缩流，则连续性方程为[15]：

(1)

而内流场范围有限，在小扰动下内充气体密度与压强相关。则可视为非定常可压缩流，其气体连续性方程为：

(2)

式中：ρ为气体密度。

在小扰动条件下，可将式(2)改写为：

(3)

根据气体密度与压强关系有[16]：

ΔP=C2Δρ

(4)

式中：ΔP为压强变化量；Δρ为密度变化量； C为音速；P为参考压强，以标准大气压作为参考压强。

(5)

式中：κ为气体体积模量。

由于速度是速度势的梯度，则式(2)可表示为：

(6)

式中：φ为气体的速度势。

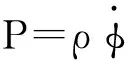
κ2φ

(7)

式(7)为线性微分方程，仅有φ一个未知量，则气体的平衡方程可以表示为：

κ∫SNFundS-κ∫VNFφ

(8)

式中：NF为整个流体的形函数向量；n为气体边界单元外法线方向；S为气固耦合边界；V为气体体积。

整理式(8)得：

(9)

1.2 膜单元平衡方程

充气膜结构的刚度来源于内充气体产生的内压。得到膜单元的静力平衡方程：

(10)

(11)

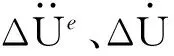
在整体坐标下对式(11)进行组装，得到充气膜结构整体的动力平衡方程为：

(12)

1.3 膜结构气固耦合

联合式(9)和式(11)，再由界面协调条件可以得到充气膜结构气固耦合动力方程为：

(13)

式中：MFF=ρMF；CFF=ρCF；MFF=ρMF。

求解充气膜结构的无阻尼自由振动，通过傅里叶变换得到：

(14)

式中：ωj是第j阶自振频率；U(j)为第j阶薄膜振型；F(j)是第j阶气体振型。

2 湿模态分析方法验证

为研究飞艇主气囊结构的模态特性，设计薄膜充气管和飞艇模型试验对分析方法进行验证。

2.1 薄膜充气管分析与试验

2.1.1 薄膜充气管模态试验

为验证湿模态分析方法应用于充气膜结构的准确性，设计ETFE薄膜充气管试验对分析结果进行验证。制作2 300 mm长的悬臂充气管，如图1所示。

图1 充气管模型(mm)Fig.1 Model of pneumatic membrane tube (mm)

试验采用带外干涉仪的激光测振器，在干涉仪中通过声光调制器 ，在40MHz或更高的驱动频率下引入载波信号。该信号与“物体频率”相调制后，通过运算，确定频率偏量相对于中心频率的符号和大小。根据测得频响曲线进行模态识别。测振系统的主要技术参数为扫描点数：512×512；频率范围：1MHz；最大速度范围：最大±10m/s，最小0.3nm/s；扫描角度：40°×40°；FFT(快速傅里叶变化)谱线：640。

试验采用一套充气系统维持充气管的内压恒定在3kPa、4kPa和5kPa。在管壁一侧使用激振器激振，为减少激振器对振型的影响，激振点选在避开各阶模态的节点位置。使用激光测振系统，在充气管另一侧测出充气管在各个内压下的固有频率与模态。充气管试验模型，如图2所示。测得充气管3kPa内压下频响曲线，如图3所示。

图2 充气管模态试验Fig.2 Modal experiment of pneumatic membrane tube

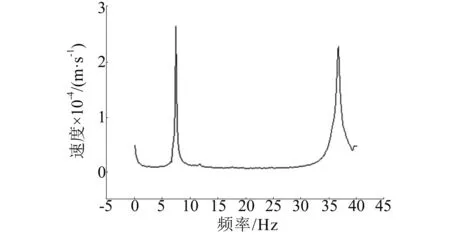
图3 充气管试验频响曲线Fig.3 Frequency response curve of pneumatic membrane tube

2.1.2 薄膜充气管模态分析

用ADINA有限元分析软件根据充气管试验参数建立充气管分析模型，模型分为结构部分和流场部分。

结构部分采用膜单元，由于ETFE薄膜在低应力阶段为线弹性各向同性材料，且具有时变特性，在模态分析中应取瞬态弹性模量。根据材料试验测定结果，取高应变率下材料参数，膜材密度ρ=1 700kg/m3，厚度t=0.2mm，弹性模量E=1 100MPa，泊松比ε=0.3。

在充气管结构内部建立空气内流场模型，周边建立矩形空气外流场模型，在充气管纵向取2倍管长，在其他方向取20倍管径模型范围，保证结构扰动能在流场中能充分发展。采用三维线性势流体单元，取20 ℃标准空气参数，空气密度ρ=1.205kg/m3，体积模量κ=10.1kPa。在结构内外建立接触面单元，保证薄膜与空气的界面协同。

根据式(4)计算出产生相应内压需要的内充气体体积，对内流场添加质量流荷载，使充气管结构达到平衡初始状态。然后采用兰索斯法(Lanczos)重启动分析对具有预应力刚度和气承刚度的充气管进行模态分析。充气管与空气势流体模型，如图4所示。

图4 薄膜充气管有限元模型Fig.4 FEA model of pneumatic membrane tube

为研究薄膜充气管湿模态分析方法，采用单面耦合和双面耦合两种方法进行分析，即仅考虑外流场与结构的耦合、仅考虑内流场与结构的耦合以及考虑内外流场与结构的耦合三种情况。结合不考虑内外流场作用，仅施加预应力刚度的干模态分析结果，确定最合理的湿模态分析方法。

针对薄膜充气管自身结构特点和模态试验测试结果，选取前2阶弯曲模态进行分析。4种分析方法得到的前2阶模态振型与试验测得振型一致。第1阶为整体平移振型，第2阶为一阶弯曲振型。模态振型对比，如图5所示。

图5 前2阶模态振型对比Fig.5 Comparison of modal shapes of first two orders

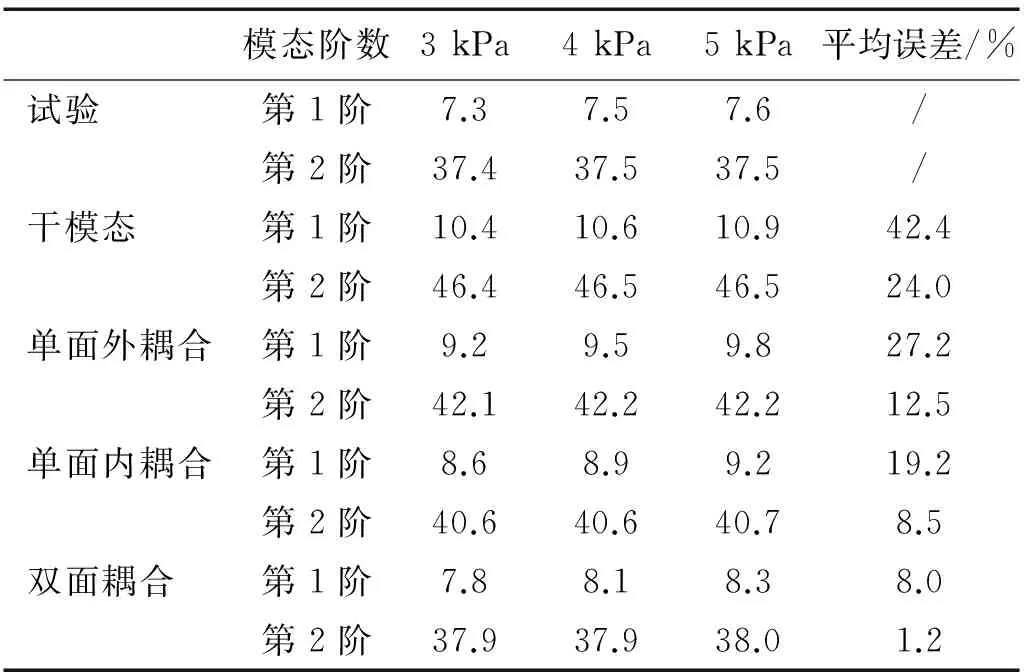
通过干湿模态分析，得到不同内压下前2阶频率，如表1所示。

表1 薄膜充气管固有频率0=kPa

Tab.1 Natural frequency of pneumatic membrane tube

Hz

干模态分析的频率值比试验值偏大较多，第1阶平均误差为42.4%，第2阶为24.0%。仅考虑外流场的单面耦合作用，第1阶平均误差为27.2%，第2阶为12.5%；仅考虑内流场的单面耦合作用，第1阶平均误差为19.2%，第2阶为8.5%；考虑内外流场双面耦合作用的结果与试验吻合最好，第1阶平均误差为8.0%，第2阶为1.2%。

分析结果表明，内外流场对充气管模态频率均有影响，且内流场的作用比外流场大，对空气中的充气膜结构进行模态分析时，不能忽略内外流场的影响，应采用双面耦合的湿模态分析方法。

随着内压的增大，前2阶弯矩模态的频率无明显增大。因为内压增大只是提高薄膜局部刚度，而当内压足够维持薄膜局部刚度后，提高内压对结构整体刚度并无贡献，在模态分析中将出现结构整体振型，文献[15]中也得到类似结论。

2.2 飞艇模型分析与试验

为进一步验证模态分析方法应用于飞艇主气囊的合理性，采用Zeppelin NT飞艇缩比模型进行模态分析和试验。Zeppelin NT是世界上最大的载人飞艇，全长75 m，可搭载14人。

2.2.1 飞艇模型模态试验

飞艇模型基本参数为艇长714.2 mm，最大直径282.2 mm，长细比2.53，体积30 695 840.0 mm3，质量141.2 g。

试验系统主要由气源、膜盒压力表、试验台架、激振器、激光测振仪和控制系统组成。本试验声波激振，减少接触式激振器对飞艇模态振型的影响。通过弹性绳将飞艇模型悬挂于试验台架上，保持飞艇处于自由状态。连接气源和压力表，在飞艇测试面均匀喷涂银光粉，在另一侧安置激振音箱，系统布置，如图6所示。

对飞艇模型充气，使内压达到2 kPa和3 kPa，待内压稳定后，使用激光测振系统，在飞艇模型一侧测出各个内压下的固有频率与模态。试验测得3 kPa下频响曲线，如图7所示。

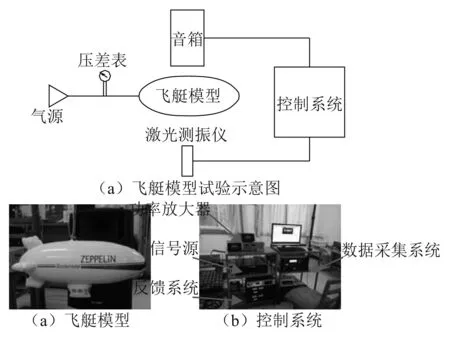
图6 飞艇模型模态试验Fig.6 Modal experiment of airship model

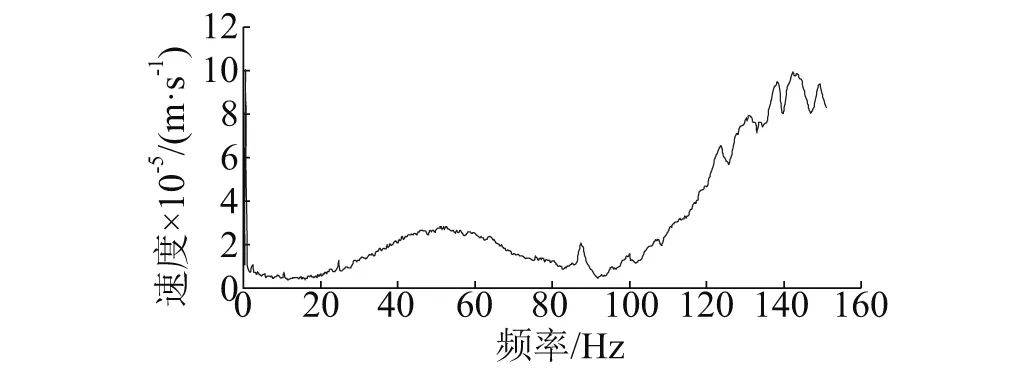
图7 飞艇模型试验频响曲线Fig.7 Frequency response curve of airship model

2.2.2 飞艇模型模态分析

根据飞艇模型参数，建立Zeppelin飞艇主气囊模态分析模型，按照薄膜充气管相同的条件，建立飞艇模型内外流场。由于飞艇模型处于自由状态，为保证主气囊在分析中不超出流场范围，增大飞艇纵向流场范围到4倍艇长。

飞艇模型的材料参数通过静力试验测得，膜材密度ρ=1 052kg/m3，厚度t=0.25mm，弹性模量E=115MPa，泊松比ε=0.34。流体参数取值同“2.1”。分析模型，如图8所示。

采取单面内耦合、单面外耦合和内外流场双面耦合三种方法进行湿模态分析，并添加干模态分析作为对照。对内流场施加质量流荷载产生内压使主气囊蒙皮获得刚度。然后用兰索斯法进行模态分析。试验与分析前3阶模态振型和模态频率对比，如图9和表2所示。

图8 飞艇模型有限元模型Fig.8 FEA model of airship model

图9 前3阶模态振型对比Fig.9 Comparison of modal shapes of first three orders

对于飞艇模型，使用四种分析方法得到的振型并不完全一致，以双面耦合的结果作为基准进行比较发现，在干模态分析中第1阶出现的振型双面耦合的第3阶模态振型。而单面耦合的前3阶振型与双面耦合相同。故在图9中列出的分析结果为双面耦合的前3阶模态振型。

由于激光测振仪仅能扫描单个平面，无法完全体现模型完整振型，故通过观察振型特征来对比试验与分析结果。从图9可知，第1阶振型为主气囊中段单侧受压，第2阶振型为两侧受压，第3阶为主气囊中段受拉与两侧受压。对比试验与分析结果，发现前3阶模态振型特征基本吻合。

表2 飞艇模型固有频率Tab.2 Natural frequency of airship model Hz

干模态分析与试验模态频率对比发现，由于模态振型的差异，对应的频率平均误差很大，均超过70%。飞艇模型与充气管模型试验结果均表现出频率不随内压增大而明显增大的特性，但在干模态分析结果未能正确体现出该特性。

单面内耦合、单面外耦合和双面耦合分析的结果均能较好地跟试验数据吻合。其中单面内耦合的前3阶的平均误差为2.9%、3.6%和2.9%，单面外耦合前3阶的平均误差为5.4%、6.2%和5.0%，双面耦合前3阶的平均误差为-3.2%、-1.4%和-2.0%。

分析表明对于飞艇结构，不考虑流场作用的干模态分析误差极大，而考虑内、单面外耦合的分析方法在一定程度上是适用的。而考虑内外流场的双面耦合湿模态分析方法与试验结果吻合最好，是分析飞艇主气囊结构模态特性的合理方法。

根据薄膜充气管和飞艇模型的分析与试验，验证并确定了采用双面耦合的方法对飞艇结构进行分析可以得到较准确的分析结果。故采用该方法对典型外形飞艇主气囊模型进行模态分析。

3 典型外形飞艇主气囊模态分析

3.1 主气囊湿模态分析

常规飞艇的主气囊接近于绕纵轴旋成的流线形体，本文采用双轴椭圆的飞艇外形，如图10所示。建立艇长为5 m、25 m、50 m和100 m，长细比1∶3、1∶3.5和1∶4的12个典型外形飞艇主气囊模型。

图10 典型外形飞艇主气囊模型Fig.10 Typical shape of airship envelop model

飞艇主气囊蒙皮材料采用高比强织物材料，等效弹性模量为706.39Mpa，泊松比为0.38，厚度为0.482mm，密度为597.82kg/m3。

为保证不同结构尺寸飞艇蒙皮具有相同的预应力刚度，根据结构相似原理[17]，确定艇长与内压的关系见表3。

表3 飞艇内压值Tab.3 Internal pressure of airship

采用同“2.2”中飞艇模型相同方法对主气囊模型进行分析，如图11和表4所示。

图11 飞艇主气囊前6阶模态振型Fig.11 First six orders modal shapes of airship envelop

忽略频率为0的刚体模态，飞艇低阶模态较密集，以图11中模态振型为前6阶进行分析。第1阶为主气囊中段单侧受压，第2阶为双面受压，第3阶为双面受拉，第4阶为艇首部分横向受压和艇尾部分竖向受压的耦合，第5阶为第1阶与第2阶模态振型的耦合，第6阶为双面受压与一阶弯曲模态的耦合。

表4 飞艇主气囊固有频率Tab.4 Natural frequency of airship envelop Hz

表4中，L为艇长，D为最大直径，L/D为长细比，p为内压。从表4可知，50 m以上大型飞艇的基频较低，提高内压不能提高结构的基频。

3.2 湿模态影响因素分析

3.2.1 艇长对湿模态的影响

为分析艇长的影响，取长细比为1∶4，内压为P3进行分析，根据表4数据绘制曲线，如图12所示。

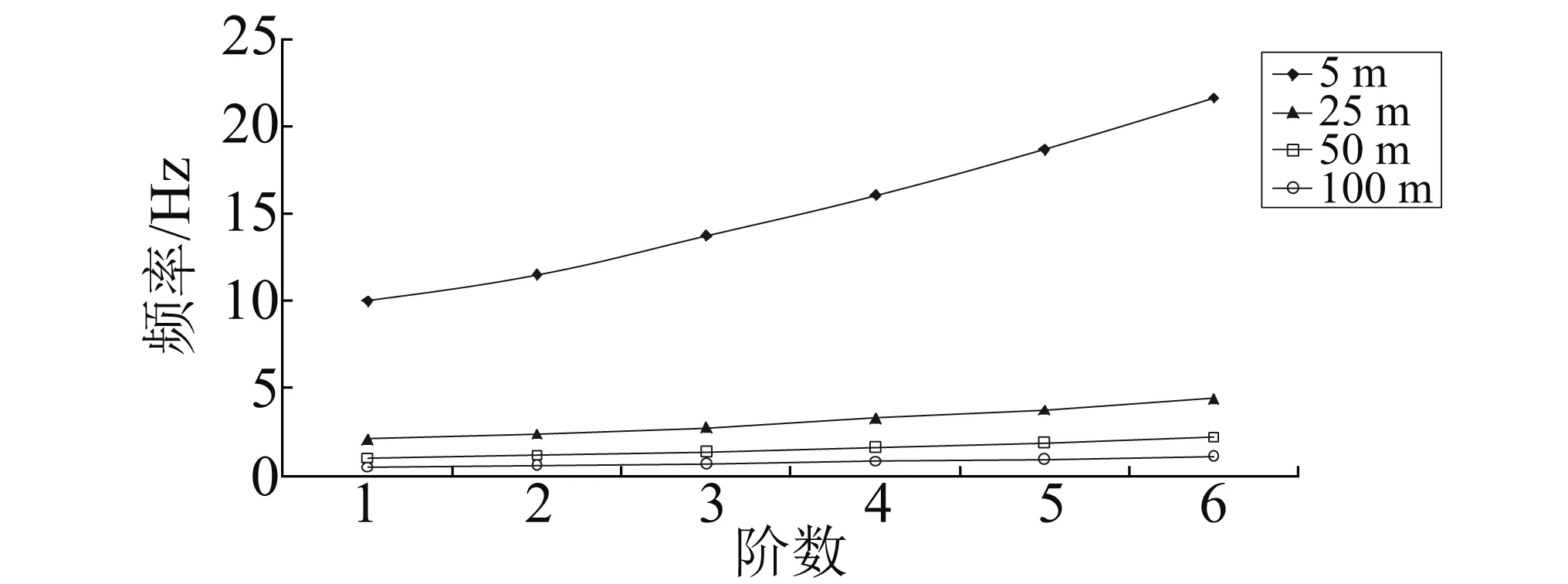
图12 艇长与固有频率关系Fig.12 Relationship of lengths and natural frequency

在相同条件下，主气囊频率随艇长增大而减小，5 m艇固有频率约为100 m艇固有频率的20倍，与相似原理结果吻合，说明飞艇模态特性的尺寸效应明显。

3.2.2 长细比对湿模态的影响

取艇长为25 m，内压为p3进行分析，根据表4数据绘制曲线，如图13所示。

图13 长细比与固有频率关系Fig.13 Relationship of slenderness ratios and natural frequency

随着长细比的变化，固有频率增长趋势相同，大小也十分接近，长细比对飞艇固有频率的影响较小。

3.2.3 内压对湿模态的影响

取艇长25m，长细比为1∶3.5进行分析。根据表4中数据绘制，如图14所示。

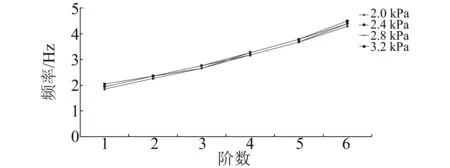
图14 内压与固有频率关系Fig.14 Relationship of internal pressures and natural frequency

随着内压的增大，主气囊固有频率无明显增大，说明在内压足够保持局部刚度之后，内压继续增大对固有频率的影响很小，与前述充气管分析与试验结果吻合。

4 结 论

本文采用流固耦合理论和势流理论，建立充气膜结构分析方法。并在考虑单面内耦合、单面外耦合和内外流场双面耦合三种情况下，对薄膜充气管与飞艇模型进行了湿模态分析，并加以模型试验对分析结果进行验证。对比分析与试验结果发现，考虑内、单面外耦合的结果在一定程度上是可接受的，但不如考虑内外流场双面耦合分析合理。

应用内外流场双面耦合方法对典型外形飞艇进行湿模态分析，发现飞艇主气囊固有频率具有明显尺寸效应，频率着艇长的增大而减小，并基本成反比关系。飞艇主气囊长细比对固有频率影响较小，飞艇主气囊结构整体模态不随内压增大而增大，内压对主气囊固有频率影响较小。

[1] 甘晓华，郭颖.飞艇技术概论[M]. 北京：国防工业出版社，2005.

[2] 王基盛, 杨庆山. 流体环境中结构附加质量的计算[J]. 北方交通大学学报, 2003, 27(1): 40-43. WANG Jisheng, YANG Qingshan. Calculation on added mass of structures in fluid environments[J]. Journal of Northern Jiaotong University,2003, 27(1):40-43.

[3] 于肖宇, 张继革, 顾卫国, 等. 薄壁圆筒结构附加质量的实验研究[J]. 水动力学研究与进展, 2010,25(5): 655-659. YU Xiaoyu, ZHANG Jige, GU Weiguo, et al. Experimental study of added mass of the thin-walled cylinder structure[J]. Chinese Journal of Hydrodynamics, 2010, 25(5):655-659.

[4] 毛国栋, 孙炳楠, 楼文娟. 膜结构的附加空气质量[J]. 工程力学, 2004, 21(1):153-158. MAO Guodong, SUN Bingnan, LOU Wenjuan. The added air-mass of membrane structures[J]. Engineering Mechanics, 2004, 21(1):153-158.

[5] 高海健, 陈务军, 付功义. 预应力薄膜充气梁模态的分析方法及特性[J]. 华南理工大学学报(自然科学版), 2010,38(7): 135-139. GAO Haijian, CHEN Wujun, FU Gongyi. Modal analysis method and modal behavior of prestressed inflatable fabric beam[J]. Journal of South China University of Technology (Natural Science Edition), 2010, 38(7):135-139.

[6] 陈宇峰, 陈务军, 何艳丽, 等. 柔性飞艇主气囊干湿模态分析与影响因素[J]. 上海交通大学学报, 2014, 48(2): 234-238. CHEN Yufeng, CHEN Wujun, HE Yanli, et al. Dry and wet modal analysis and evaluation of influencing factors for flexible airship envelop[J]. Journal of Shanghai Jiao Tong University, 2014, 48(2):234-238.

[7] LI Y Q, WANG L, SHEN Z Y, et al. Added-mass estimation of flat membranes vibrating in still air [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2011, 99(8): 815-824.

[8] 王磊, 李元齐, 沈祖炎. 薄膜振动附加质量试验研究[J]. 振动工程学报, 2011, 24(2): 125-132. WANG Lei, LI Yuanqi, SHEN Zuyan. Experimental investigation on the added mass of membranes vibrating in air[J]. Journal of Vibration Engineering, 2011, 24(2):125-132.

[9] EPUREANU B I, HALL K C, DOWELL E H. Reduced-order models of unsteady viscous flows in turbomachinery using viscous-inviscid coupling[J]. Journal of Fluids and Structures, 2001, 15(2): 255-273.

[10] 毛国栋, 孙炳楠, 楼文娟, 等. 膜结构风振响应计算中的流固耦合因素研究[J]. 振动工程学报, 2004, 17(2): 228-232. MAO Guodong, SUN Bingnan, LOU Wenjuan, et al. Analysis of the fluid-structure coupling factors for wind-induced dynamic response of membrane structures[J]. Journal of Vibration Engineering, 2004, 17(2):228-232.

[11] 陈宇峰，陈务军，邱振宇，等. 空气对预应力薄膜结构模态的影响[J]. 浙江大学学报(工学版)，2015,49(6):1123-1127. CHEN Yufeng, CHEN Wujun, QIU Zhenyu, et al. Effects of airon modal behavior of pre-stressed membrane structure[J]. Journal of Zhejiang University (Engineering Science),2015, 49(6):1123-1127.

[12] 李鹏, 杨庆山. 内充气体与外部膜材的共同作用理论模型[J]. 力学学报, 2013, 45(6):919-927. LI Peng, YANG Qingshan. Interaction model of the enclosed air and the outer membrane[J]. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(6):919-927.

[13] 宋月萧，杨庆山. 气枕式膜结构的模态分析[C] ∥第十二届空间结构学术会议.北京, 2008:217-222.

[14] 余建新, 卫剑征, 谭惠丰. 薄膜充气环动态特性试验研究[J]. 振动与冲击, 2013, 32(7): 11-16. YU Jianxin, WEI Jianzheng, TAN Huifeng. Tests for thin film inflatable toruses[J]. Journal of Vibration and Shock, 2013,32(7):11-16.

[15] 孙祥海. 流体力学[M].上海:上海交通大学出版社, 2000.

[16] LIAO L, PASTERNAK I. A review of airship structural research and development[J]. Progress in Aerospace Sciences, 2009, 45(4): 83-96.

[17] 周利霖，唐国金. 大型飞艇缩比模型设计方法研究[C] ∥第三届高分辨率对地观测学术年会.长沙,2014:234-251.

Wet modal analysis and experiment study on an airship envelop

QIU Zhenyu, CHEN Wujun, ZHAO Bing, GAO Chengjun, YU Zhengyue

(Space Structures Research Centre, Shanghai Jiao Tong University, Shanghai 200240, China)

In order to analyze the modal characteristics of an airship envelop, the air around the airship envelop was assumed as potential fluid, and based on the FSI (Fluid Structure Interaction) theory and potential flow theory, the theory on the membrane and the air flow field interaction was presented. Also a numerical method for pneumatic structure modal analysis is was applied to study the pneumatic membrane tube and the airship model. Inner side coupling, outer side coupling, and both sides coupling method were considered and compared, and experiments on the same subject demonstrate the validity of these the methods. It shows that the both sides coupling method is more suitable for pneumatic structure modal analysis. Therefore modal analyses on the airship envelop with the slenderness ratios of 1∶3, 1∶3.5 and 1∶4, and the lengths of 5 m, 25 m, 50 m and 100 m were completed, and it shows that natural frequency is in inverse proportional to the length of the airships, while the influence of slenderness ratios and internal pressures is little. The results can provide a reference for airship structure design and modal analysis of complex shape pneumatic membrane.

airship envelop; modal analysis; potential fluid; wet mode; Fluid Structure Interaction(FSI)

国家自然科学基金(51278299；51478264)

2015-10-10 修改稿收到日期： 2016-03-10

邱振宇 男，博士生，1984年生

陈务军 男，博士，研究员，1969年生

V214.3+3

A

10.13465/j.cnki.jvs.2017.12.011