3类特殊图完美匹配数的计算公式*

唐保祥，任韩

(1. 天水师范学院数学与统计学院，甘肃 天水 741001； 2. 华东师范大学数学系，上海 200062)

3类特殊图完美匹配数的计算公式*

唐保祥1，任韩2

(1. 天水师范学院数学与统计学院，甘肃 天水 741001； 2. 华东师范大学数学系，上海 200062)

图的完美对集计数问题已经被证实是NP—难问题，因此要得到一般图的完美对集的数目是非常困难的。该问题在蛋白质结构预测、晶体物理学、计算机科学和量子化学中都有重要的应用，对此问题的研究具有非常重要的理论价值和现实意义。用划分，求和，再递推的方法分别给出了图3-nT4，5-nT6和2-2nQ2×2的完美匹配数目的计算公式，为图的完美匹配问题的应用提供了理论支持。

完美匹配；梯子；递推式；棋盘

图的完美匹配计数理论的研究成果已经在化学、物理学和计算机科学中得到应用,图的完美匹配的理论在很多领域有广泛应用，例如：积和式在计算机科学，特别是计算复杂性理论中有重要的地位，二分图的完美匹配的数目可以方便地表示为计算积和式的值;它也是组合数学的思想源泉，因此受到众多学者的关注[1-14]，本文给出了3类图完美匹配数目的计算公式，文中所给方法，适合相同结构重复出现的很多类图完美匹配数的求解。

1 基本概念

定义1 两条长为n的路为P1=u1u2…un+1，P2=v1v2…vn+1，分别连接路P1与P2的顶点ui与vi(i=1,2,…,n+1)所得到的图，称为长为n的梯子，记为Tn。

定义2 设m+1条长为n的路Pi=ui1ui2ui3…ui,n+1(i=1,2,…,m,m+1)，连接路Pi与Pi+1中的顶点uij与ui+1,j(i=1,2,…,m;j=1,2,…,n,n+1)所得的图，称为m×n的棋盘。本文将m×n的棋盘记为Qm×n。

定义3 若图G的两个完美匹配M1和M2中有一条边不同，则称M1和M2是G的两个不同完美匹配。

图1 1-nT2图Fig.1 Figure of 1-nT2

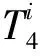
图2 3-nT4图Fig.2 Figure of 3-nT4

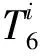
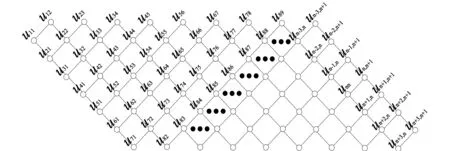
图3 5-nT6图Fig.3 Figure of 5-nT6

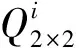
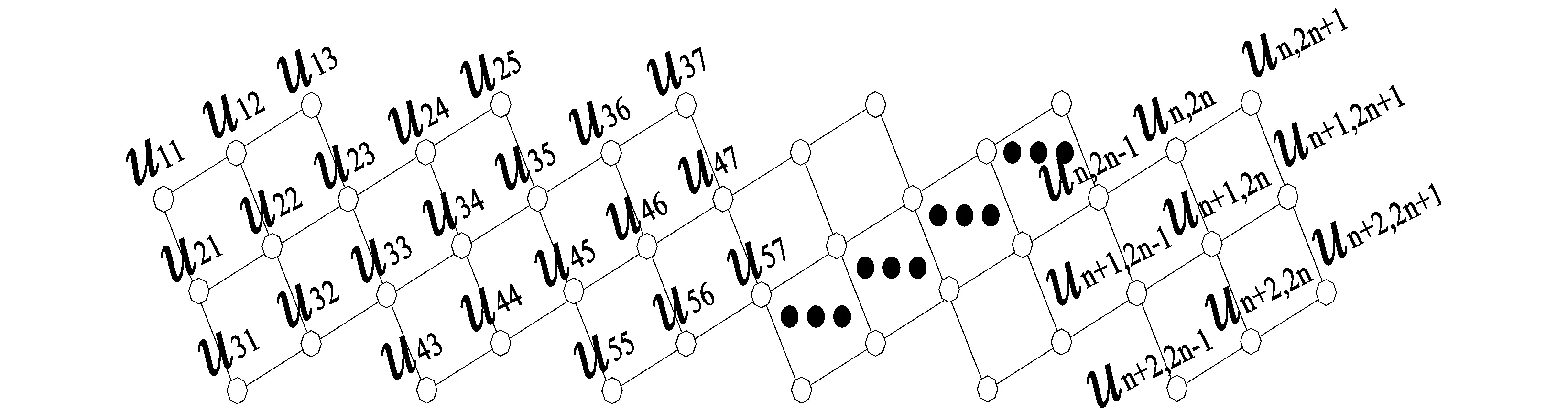
图4 2-2nQ2×2图Fig.4 Figure of 2-2nQ2×2

2 结果及其证明

引理 1[9]f(n)表示1-nT2图的所有不同的完美匹配数，其中n=1,2,3,…，则f(n)=2n+1。

定理1g(n)表示3-nT4图的所有不同的完美匹配数，其中n=1,2,3,…，则g(n)=2n(n+3)。

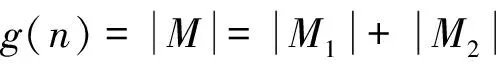
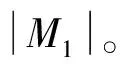
情形1u11u12,u21u22∈M1

因为u11u12,u21u22∈M1，所以u23u33,u34u44,u45u55,…,un,n+1un+1,n+1∈M1。由引理1中f(n)的定义知，M1中这类完美匹配的数目为f(n)。

情形2u11u12,u21u31,u41u51∈M1

由g(n)的定义知，M1中这类完美匹配的数目为g(n-1)。

情形3u11u12,u21u31,u41u42,u51u52∈M1

因为u11u12,u21u31,u41u42,u51u52∈M1，所以

u62u63,u73u74,…,un+4,nun+4,n+1,u43u53,u54u64,…,

un+2,n+1un+3,n+1,u34u44,u45u55,…,un,n+1un+1,n+1∈M1

M1中这类完美匹配的数目与4圈u22u23u33u32u22的完美匹配数相等。故M1中这类完美匹配的数目为2。

综上所述，g(n)=2f(n)+g(n-1)+2。

因为f(n)=2n+1，所以

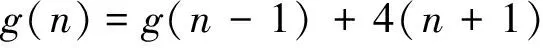
(1)

解递推式(1)，得

易知g(1)=8，所以g(n)=2n(n+3)。

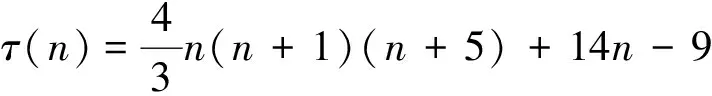
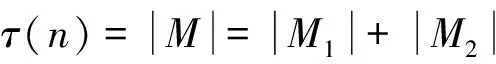
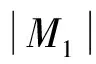
情形1u11u12,u21u22∈M1。

因为u11u12,u21u22∈M1

所以

由定理1中g(n)的定义知，M1中这类完美匹配的数目为g(n)。

情形2u11u12,u21u31,u41u51,u61u71∈M1。

由τ(n)的定义知，M1中这类完美匹配的数目为τ(n-1)。

情形3

因为u11u12,u21u31,u41u51,u61u62,u71u72∈M1,所以

M1中这类完美匹配的数目与图G=(V(G),E(G))的完美匹配数相等。其中

故M1中这类完美匹配的数目为6。

情形4

因为

所以

所以M1中这类完美匹配的数目与4圈u22u23u33u32u22的完美匹配数相等。故M1中这类完美匹配的数目为2。

情形5

由

知

所以M1中这类完美匹配的数目与4圈u22u23u33u32u22的完美匹配数相等。故M1中这类完美匹配的数目为2。

情形6

由

u11u12,u21u31,u41u42,u51u61,u52u62,u71u72∈M1

知

u82u83,u93u94,u10,4u10,5,u11,5u11,6,…,un+6,nun+6,n+1,

un+5,n+1un+4,n+1,un+3,n+1un+2,n+1,un+1,n+1un,n+1,…,

u45u55,u34u44∈M1

所以M1中这类完美匹配的数目与4圈u22u23u33u32u22的完美匹配数相等。故M1中这类完美匹配的数目为2。

情形7

因为

所以

所以M1中这类完美匹配的数目与4圈u22u23u33u32u22的完美匹配数相等。故M1中这类完美匹配的数目为2。

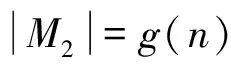
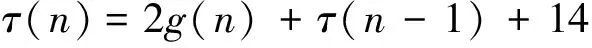
因为g(n)=2n(n+3)，所以

(2)

易知τ(1)=21。解递推式(2)，得

定理3σ(n)表示图2-2nQ2×2的所有不同的完美匹配数，其中n=1,2,3,…，则σ(n)=16·10n-1。

证明 易知2-2nQ2×2图有完美匹配。为了求2-2nQ2×2图的完美匹配的数目，首先定义图G，并求其完美匹配的数目。设v1v2v3v4v1是个4圈，uv是一条路。将2-2nQ2×2图的顶点u11,u21分别与顶点v2,v3各连结一条边;再将顶点u,v分别与顶点v2,u11各连结一条边所得的图记为G，如图5所示。

图5 G图Fig.5 Figure of G

易知图G有完美匹配。h(n)表示图G的完美匹配数。设G的完美匹配集合为M(G)，图G含边v1v2,v1v4的完美匹配集合分别为M(G)1,M(G)2，则M(G)i≠∅(i=1,2)，M(G)1∩M(G)2=∅，所以M(G)=M(G)1∪M(G)2。

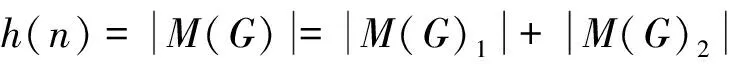
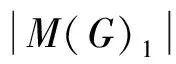
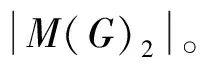
情形1

v1v4,v2v3,uv∈M(G)2

由σ(n)的定义知，M(G)2中此类完美匹配的数目为σ(n)。

情形2

情形2.1

v1v4,uv2,vu11,v3u21,u31u32,u12u22,u13u23∈M(G)2

由h(n)的定义知，M(G)2中此类完美匹配的数目为h(n-1)。

情形2.2

由h(n)的定义知，M(G)2中此类完美匹配的数目为h(n-1)。

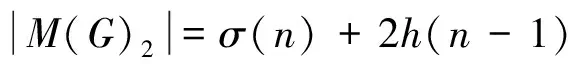
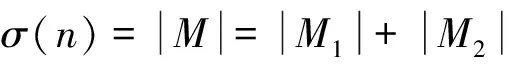
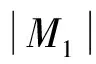
情形1

由h(n)的定义知，M1中此类完美匹配的数目为h(n-1)。

情形2

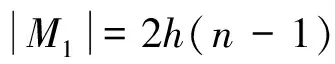
情形1

由h(n)的定义知，M2中此类完美匹配的数目为h(n-1)。

情形2

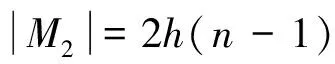
综上所述，

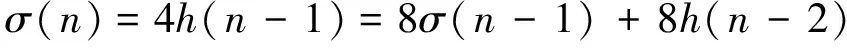
因为h(n)=2σ(n)+2h(n-1)，所以有

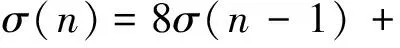
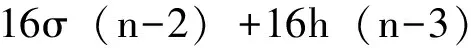
(3)

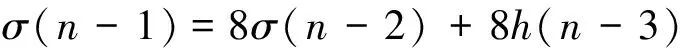
(4)

由式(3)-2×(4)，得

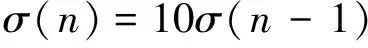
(5)

解递推式(5)，得σ(n)=10n-1σ(1)。易知σ(1)=16，故σ(n)=16·10n-1。

[1]LOVSZL,PLUMMERM.Matchingtheory[M].NewYork:North-HollandPress, 1986.

[2]CIUCUM.Enumerationofperfectmatchingsingraphswithreflectivesymmetry[J].JCombinTheorySerA, 1998, 77(1): 67-97.

[3]JOCKUSCHW.Perfectmatchingsandperfectsquares[J].JournalofCombinatorialTheory, 1994, 67(1):100-115.

[4]ZHANGHP.TheconnectivityofZ-transformationgraphsofperfectmatchingsofpolyominoes[J].DiscreteMathematics, 1996, 158: 257-272.

[5]ZHANGHP,ZHANGFJ.Perfectmatchingsofpolyominographs[J]. Graphs and Combinatorics, 1997, 13(3): 295-304.

[6] YAN W G, ZHANG F J. Enumeration of perfect matchings of a type of Cartesian products of graphs [J]. Discrete Applied Mathematics, 2006, 154(1):145-157.

[8] KARDOS F, KRL D, MISKUF J, et al. Fullerene graphs have exponentially many perfect matchings [J]. Journal of Mathematical Chemistry, 2009, 46(2): 443-447.

[9] 唐保祥，任韩. 2类图完美匹配数目的解析式[J]. 中山大学学报(自然科学版), 2016, 55(4): 15-17. TANG B X, REN H. The analytic formula of the number of perfect matchings of two types of graphs [J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2016, 55(4): 15-17.

[10] 唐保祥，任韩. 3类3-正则图中的完美对集数[J]. 南京师大学报(自然科学版), 2016, 39(1): 21-24. TANG B X, REN H. The number of perfect matchings in two types of 3-regular graph [J]. J of Nanjing Normal University (Natural Science Edition), 2016, 39(1): 21-24.

[11] 唐保祥，任韩. 3类特殊图完美对集数的计算[J]. 南开大学学报(自然科学版), 2014, 47(5): 11-16. TANG B X, REN H. The enumeration of perfect matchings in three types of special graphs [J]. Acta Scientiarum Naturalium Universitatis Nankaiensis, 2014, 47(5): 11-16.

[12] 唐保祥，任韩. 4类图完美匹配数目的递推求法[J]. 数学杂志, 2015, 35(3): 626-634. TANG B X, REN H. Recursive method for finding the number of perfect matchings of the four types of graphs [J]. J of Math, 2015, 35(3): 626-634.

[13] 唐保祥，任韩. 两类3正则图中的完美匹配数[J]. 中山大学学报(自然科学版), 2014, 53(5): 54-58. TANG B X, REN H. The number of perfect matchings in two types of 3-regular graph [J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2014, 53(5): 54-58.

[14] 唐保祥，任韩. 6类图完美匹配的数目[J]. 中山大学学报(自然科学版), 2012, 51(2): 40-44. TANG B X, REN H. The number of perfect matchings in six types of graphs [J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2012, 51(2): 40-44.

The counting formula of the perfect matchings of three types of special graphs

TANGBaoxiang1,RENHan2

(1. School of Mathematics and Statistics, Tianshui Normal University, Tianshui 741001, China; 2. Department of Mathematics, East China Normal University, Shanghai 200062, China)

Perfect matching counting problems graph has been proven to be NP-hard. To get the number of perfectly matched general graph is very difficult. The issue has important applications in protein structure prediction, crystal physics, quantum chemistry and computer science. The research on this issue has very important theoretical and practical significance. The counting formula of the perfect matching for graphs 3-nT4, 5-nT6and 2-2nQ2×2are obtained by applying differentiation, summation and re-recursion . This provides the theory support for the application of perfect matching in graph.

perfect matching; ladder; recurrence relation; chessboard

10.13471/j.cnki.acta.snus.2017.03.006

2016-08-05 基金项目：国家自然科学基金 (11171114)

唐保祥(1961年生)，男；研究方向：图论和组合数学；E-mail : tbx0618@sina.com

O157.5

A

0529-6579(2017)03-0036-05