弹载爆磁压缩发生器动态电感的计算

黄 旭，吕庆敖，雷 彬，向红军，孟学平

(军械工程学院 弹药工程系，河北 石家庄 050003)

弹载爆磁压缩发生器动态电感的计算

黄 旭，吕庆敖，雷 彬，向红军，孟学平

(军械工程学院 弹药工程系，河北 石家庄 050003)

动态电感在弹载爆磁压缩发生器的设计计算中具有举足轻重的地位。为了解决动态电感的计算问题，将镜像电流模型运用到了某弹载爆磁压缩发生器的电路参数计算中，并进行了详细的推导，编写了一个弹载爆磁压缩发生器动态电感的数值计算程序。代入设计数据计算后，获得了电感变化曲线，分析得出了发生器运行过程中电感变化的阶段性特点，为下步优化设计及试验提供了依据。

脉冲功率电源；爆磁压缩发生器；电感计算；镜像电流；MATLAB

爆磁压缩发生器(MFCG)是一种通过释放炸药化学能使导体运动做功并压缩种子磁通、实现瞬间发电的脉冲功率发电装置。作为体积小、质量轻的脉冲功率发电装置，爆磁压缩发生器可以作为电磁脉冲弹等新型弹药的弹载电源。

1 弹载MFCG模型

根据某型100 mm弹载平台要求，设计了多段式螺线圈型爆磁压缩发生器，结构如图1所示，其中左侧为MFCG，右侧直接连接战斗部。

管状电枢材料为铝，线圈材料为紫铜。其中，铝电枢内直径为45 mm，长度为130 mm，壁厚3.8 mm；电枢内装黑索金炸药，在直径45 mm时的爆速约为6 400m/s；发生器的线圈外径100 mm，总长为100 mm，分成两段，其长度为l1=l2=50 mm，第1段由导电截面为4 mm2的单股导线绕制而成，匝数N1=11,第2段由相同导线2根并联绕制而成，匝数N2=6，其线圈各段参数如表1所示。另外根据战斗部作用要求，用铜线绕制线圈作为负载，其负载电感Ld=0.443 μH。由铜的电导率σCu=5.755×107(Ω·m)-1,可得到负载电阻Rd=0.695 mΩ。

表1 螺线圈各段数据

在适当时机，经由雷管引爆猛炸药，随后炸药将一方面沿径向推动电枢扩张变形;另一方面沿轴向传递爆轰波。通过Gurney模型[1-2]计算来估计电枢动力学，可以得到管状电枢在炸药作用下形成锥角约为12°的锥体向右运动，并不断接触、短路线圈，使发生器电感减少。动态电感的计算理论将根据此运行过程来建立。

2 弹载MFCG的动态电感计算理论

爆磁压缩发生器的等效电路图如图2所示，大致可看成发生器电感Lg(t)、电阻Rg(t)和负载电感Ld、电阻Rd的串联回路[3-4]。当开关K1闭合时，种子电流源C为发生器充电形成种子磁通，此时回路电流为i(0)；当i(t)上升到一定幅值时，开关K2闭合且Lg(t)快速减少，根据磁通守恒原理，回路中将产生强大的电流[5]。整个过程中动态电感Lg(t)是个难以控制且不易测量的关键参数，因而爆磁压缩发生器动态电感的计算会直接影响到其设计时的效果估计。

根据爆磁压缩发生器等效电路理论，发生器的运行效果可由等效电感Lg(t)的变化来估算。由MFCG工作过程可知，螺线圈型爆磁压缩发生器的等效电感Lg(t)和等效直流电阻Rg(t)是个随时间变化的函数。由于铝电枢厚度3.8 mm远大于感应电流的趋肤深度，故有全反射及镜像电流的假设。计算可采用镜像电流模型[6]，在此作出如下假设：

1) 电枢上感应的电流方向与线圈电流方向相反，大小相同且具有相同的导电截面。

2) 当电枢膨胀时，电枢上的等效电流环的半径不断扩大，直到与线圈接触，合并成一个导电圆环。

3) 电枢为良导体，不考虑电枢中的磁通损耗。

4) 计算电阻时认为温度维持在室温。

计算动态电感时，将线圈上每一根导电线和电枢上镜像电流的每一对应导电路径都简化成导电圆环，圆环的自感计算公式为[7]

(1)

式中：a为圆环的导电截面半径；r为圆环半径；μ0为真空磁导率。

设发生器的总电感为Lg(t);螺线圈的电感为Ls，螺线圈的电阻为Rs，所流过的电流为Is；电枢的电感为La，电枢的电阻为Ra，所流过的电流为Ia;线圈与电枢之间的互感为M。容易得到它们之间的关系Lg(t)=Ls+La+M和Is=Ia=i(t)。

线圈与电枢中的电流方向相反，若将线圈与电枢看成两个独立的回路，则线圈和电枢的回路方程都可表示为[8-9]

(2)

根据假设3)，则Ra=0，因为电枢初始磁通为0，于是有

(3)

再加上能量守恒方程，一起代入式(2)，整理得

(4)

其中线圈、电枢的自感及它们之间的互感为[7]

(5)

(6)

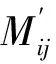
(7)

(8)

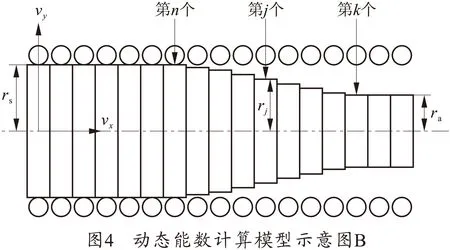
式中:ri、rj是所求互感的两个圆环的半径；Xij是所求互感的两个圆环之间的轴向距离；K(k)和E(k)是具有模数k的第一类和第二类全椭圆积分。

对于动态能数n和电枢某个等效圆环半径rj可能出现如下两种情况：

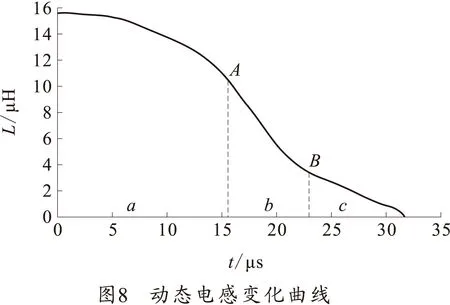
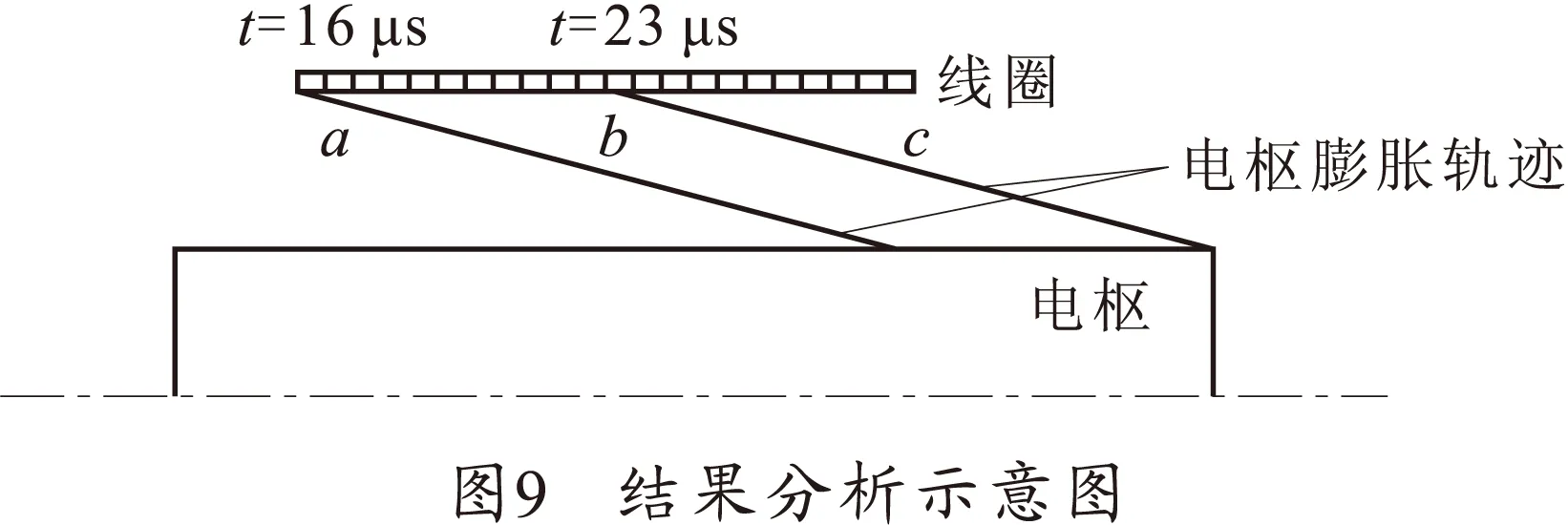
1)雷管起爆后(t>0)且电枢接触线圈前(t

图3中，k表示第k个等效圆环刚刚起爆，在这种情况下n=k。t=0时引爆雷管，设径向爆轰波速为vy=Dtanα，轴向爆轰波速为vx=D,其中D为炸药爆速。则电枢从起爆到接触线圈的时间为t0=(rs-ra)/vy，爆轰波扫过第1段的时间为t1=l1/vx，其中rs为线圈内半径，ra为电枢外半径，t0>t1[10]。

所以

(9)

式中，P为相邻两电枢导电圆环的轴向距离。

此时，第k个圆环的半径rk=ra，而任意第j个圆环的半径为

rj=ra+|n-j|Ptanα

(10)

2)撬断开关接通后(t>t1)。

如图4所示，此时n表示第n个电枢圆环刚与线圈接触，同理有

(11)

此时，第n个圆环的半径rn=rs，第k个圆环的半径rk=ra，而任意第j个圆环的半径为

rj=rs-P(j-n)tanα

(12)

由于分段螺距不同，第i个圆环和第j个圆环之间的轴向距离Xij具有特殊性:

1)当i,j≤N1时，Xij=|i-j|P1。

2)当i,j>N1时，Xij=|i-j|P2。

3)当i(j)≤N1且j(i)>N1时，Xij=P1[N1-i(j)]+P2[j(i)-N1]。

3 数值计算

根据前述计算方法[8]，使用MATLAB编写的计算编码程序流程图,如图5～7所示。

对上述弹载爆磁压缩发生器的动态电感进行数值计算，取数据量为100个，得到动态电感的变化曲线如图8所示。其中A点为电枢接触线圈的时刻，约为16 μs，B点为电枢接触两股并绕线圈部分的时刻，约为23 μs。整个曲线可以分为3段；a段从0—16 μs，为加速下降段；b段从16—23 μs，为快速下降段；c段从23 μs开始到结束，为平稳下降段。

对应的分析示意图如图9所示，a段中电枢还未开始短路线圈圆环，只在空间有限地压缩磁通，且压缩的空间逐渐增大，因而可以观察曲线斜率在不断增大；b段中电枢在爆轰能量的作用下快速短路第1段线圈的各个圆环，造成了电感的迅速下降，具有整条曲线中最大的斜率；而c段中电枢运动到了导电圆环变成2倍宽度的第2段线圈，短路速度减半，曲线的斜率也随之改变。

最后可得到装置初始电感Lg(0)约为15.558 μH，末电感Lg(tf)约为0.244 μH，运行时间tf约为31.388 μs，亦即该发生器在理想状态下具有近64倍的电感变化幅度。

4 结束语

根据某型破甲弹设计的弹载平台多段式螺线圈型爆磁压缩发生器在结构上有其特殊性，其动态电感的计算也具有自己的特点。镜像电流法是爆磁压缩发生器电路参数计算的一种重要的计算方法，能有效简化爆磁压缩发生器运行参数的计算过程。将镜像电流法应用到弹载爆磁压缩发生器的设计验证计算中，得到了15.558 μH的初始电感和0.244 μH的终末电感，简单明了地显示出初始设计的预计效果，为弹载爆磁压缩发生器结构等参数的调整提供了依据，提高了优化设计的效率。

References)

[1]MILLER P J,ALEXANDER K E. Determining JWL equation of state parameters using the gurney equation approximation[C]∥Proceeding of the 9th International Symposium on Detonation.Portland, USA:IEEE,1989:489- 505.

[2]KESHAVARZ M H, SEMNANI A. The simplest method for calculating energy output and gurney velocity of explosives[J]. Journal of Hazardous Materials, 2006, 131(1):1-5.

[3]王莹. 高功率脉冲电源[M]. 北京:原子能出版社,1991. WANG Ying. High power pulse source[M]. Beijing: Atomic Energy Press, 1991. (in Chinese)

[4]LYU Q A,LEI B,GAO M,et al.Magnetic flux compression generator as future military pulsed power supply[J].IEEE Transactions on Magnetics,2009,45(1):545-549.

[5]ALTGILBERS L L, BROWN M, GRISHNAEV I, 等. 磁通量压缩发生器[M]. 孙承纬,周之奎,译. 北京：国防工业出版社,2008. ALTGILBERS L L, BROWN M D J, GRISHNAEV I, et al. Magnetocumulative Generators[M]. SUN Chengwei, ZHOU Zhikui, translated. Beijing: National Defense Industry Press, 2008. (in Chinese)

[6]陈冬群. 动态级联型螺线管爆磁压缩发生器研究[D]. 长沙:国防科学技术大学, 2005:44-45. CHEN Dongqun. Dynamic cascading solenoid MFCG research[D]. Changsha: National University of Defense Technology, 2005:44-45. (in Chinese)

[7]卡兰塔罗夫 П Л, 采伊特林 Л А. 电感计算手册[M]. 陈汤铭, 刘保安, 罗应立，等译. 北京:机械工业出版社, 1992. КАЛАНТАРОВ П Л, ЦЕЙТЛИН Л А. Inductance calculation manual[M]. CHEN Tangming, LIU Bao’an, LUO Yingli, et al translated. Beijing:China Machine Press, 1992. (in Chinese)

[8]HAURYLAVETS V V, TIKHOMIROV V V. Mathematical simulation of helical flux compression generator physics[J]. Mathematical Models and Computer Simulations, 2013, 5(4): 334-337.

[9]孙奇志. 轴线起爆式螺线管型爆磁压缩发生器理论模型和原理性实验研究[D]. 绵阳:中国工程物理研究院, 2002:21. SUN Qizhi. Models and principles of the generator with a theory initiated axially helical magnetic compression[D]. Mianyang: China Academy of Engineering Physics, 2002:21. (in Chinese)

[10]孔斌. 非核爆磁通压缩发生器数值模拟与实验研究[D]. 南京:南京理工大学, 2007:39-41. KONG Bin. Numerical simulation and experimental study of non-nuclear magnetic flux compression generator[D]. Nanjing: Nanjing University of Science and Technology, 2007:39-41. (in Chinese)

Calculation of Dynamic Inductance for Projectile-borneMagnetic Flux Compression Generator

HUANG Xu, LYU Qing’ao, LEI bin, XIANG Hongjun, MENG Xueping

(Department of Ammunition Engineering, Ordnance Engineering College, Shijiazhuang 050003,Hebei,China)

The dynamic inductance is significant for projectile-borne magnetic flux compression gene-rator (MFCG) design calculation. For the purposes of solving the problem of dynamic inductance calculation, image current model was applied to the circuit parameters calculation of a projectile-borne MFCG. And the dynamic inductance expression was derived in detail. Subsequently, a numerical computation program of projectile-borne MFCG dynamic inductance was written within deriving process. Curve of inductance change was achieved after computing through calculating with the design parameters, with phasic characteristic of inductance variation analyzed during generator operation, which provides grounds for the next-step optimized design and experiments.

pulsed power supply; MFCG; inductance calculation; image current; MATLAB

2016-05-06

国家自然科学基金项目(51307182)

黄旭(1991—)，男，硕士研究生，主要从事脉冲功率技术研究。E-mail：475624469@qq.com

10.19323/j.issn.1673- 6524.2017.02.010

TN86

A

1673-6524(2017)02-0044-05