反坦克火箭筒横倾状态下射击偏差的定量分析

周永强，焦方金

(1.石家庄陆军指挥学院，河北 石家庄 050084；2.石家庄机械化步兵学院，河北 石家庄 050083)

反坦克火箭筒横倾状态下射击偏差的定量分析

周永强1，焦方金2

(1.石家庄陆军指挥学院，河北 石家庄 050084；2.石家庄机械化步兵学院，河北 石家庄 050083)

反坦克火箭筒发生横向倾斜时会影响火箭弹的射击精度，导致射击出现偏差。通过建立反坦克火箭筒的坐标系，描述反坦克火箭筒横倾前后的筒身状态，通过分析和坐标变换，得出横倾状态下射击偏差量的数学模型。利用Origin软件，计算了使用典型弹种射击时，反坦克火箭筒在不同距离、不同横倾角度下的方向和高低偏差量。通过对计算结果的分析表明，横倾造成的方向和高低偏差量，随着射击距离和横倾角的增大而增大，但是对于火箭弹的射击精度影响程度不同，高低偏差量极小，可以忽略不计，方向偏差量较大，需要进行修正。该计算方法和结论可为制定精确射表提供参考。

工程数学；反坦克火箭筒；横倾；修正量

反坦克火箭筒是一种破甲威力大、使用灵活方便且相对低廉的反坦克武器，能够在复杂地形条件下对固定目标进行射击。该火箭筒分为营用型和连用型两种，连用型火箭筒通常采用肩扛发射，射击距离较近；营用型火箭筒通常采用有架射击而且配备有简易火控，能够进行激光测距、自动解算射击诸元并以光点的形式显示瞄准点，射击距离较远，精度较高。在营用型火箭筒的简易火控内安装有倾角传感器用于测量射击时火箭筒的横向倾角，并利用简易火控进行修正。但是火控在修正偏差量时，只是修正了横倾导致的方向偏差量而没有修正表尺偏差量，对于该种修正方法的原因，教材及火控说明书中均未给予说明[1-2]，因此，笔者通过建立倾角偏差量计算模型来实际计算火箭筒横倾状态下射击引起的火箭弹方向及表尺偏差量，并以计算结果为基础，分析了火控采用该种修正方法的原因。

1 建立坐标系

建立反坦克火箭筒的直角坐标系，以描述反坦克火箭筒横倾前后的筒身状态。由于营用型反坦克火箭筒是以三脚架的耳轴固定器为支点进行方向和高低旋转的，因此建立以该支点为坐标原点的直角坐标系。坐标系以O-XYZ表示，O为坐标原点，为反坦克火箭筒筒身轴线与三脚架耳轴固定器的交点；X轴表示火箭筒在O点所在水平面上的投影，指向前方；Y轴表示垂直于X轴指向右侧的射线；Z轴指向正上方[3]。

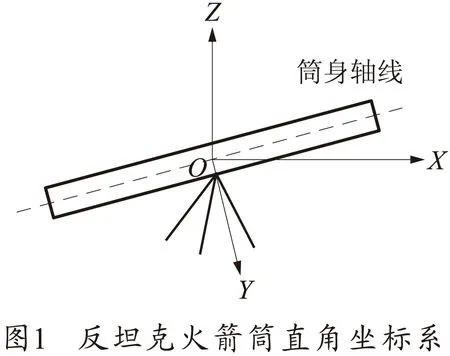
2 初始状态与横倾状态的坐标变换

设定火箭筒初始状态下高低射角为α0，方向射角为0，以P0代表其初始状态的矢量,x0、y0、z0为筒身的坐标，则P0=[x0y0z0]，其矢量P0的长度为L0。

火箭筒横倾后，其高低射角和方向射角均会发生变化，假设其横倾角度为θ，横倾后的高低射角为α，方向射角为β，以P代表发生横倾状态下的火箭筒矢量，x、y、z为横倾后筒身的坐标，则P=[xyz]，其矢量P的长度为L。

P0与P在火箭筒直角坐标系中的位置关系如图2所示。

设T为P0与P的转换矩阵，则有：

P=P0T

(1)

由图2中矢量P0和P的位置关系，可求得转换矩阵为

将转换矩阵T代入式(1)，可以求得：

[x0y0cosθ+z0sinθz0cosθ-y0sinθ]

(2)

3 计算射击偏差量

3.1 射击偏差量计算

根据式(1)可得如下方程式：

(3)

由于初始状态下，P0的方向角度为0，所以其在Y轴上的分量为0，所以P0=[x00z0]，其长度L0与其在3个坐标轴上的分量有如下关系：

(4)

横倾后，矢量P的高低、方向角度均发生变化，长度L与其在3个坐标轴上的分量有如下关系：

(5)

将式(4)、(5)带入式(3)，可得：

(6)

由于火箭筒只发生了横向倾斜，即矢量P0和P只围绕X轴方向发生旋转，所以矢量P0和P的长度是相等的，即L0=L。

因此，式(6)消去长度矢量后，可变为：

(7)

要想计算火箭筒横倾引起的方向和高低射角偏差量，需要知道其横倾后的高低射角α和方向射角β，将式(7)进一步简化后可得出横倾后的方向射角、高低射角为

(8)

所以横倾引起的方向偏差量Δβ、高低偏差量Δα分别为

Δβ=β-0=arctan(tanα0sinθ)

(9)

Δα=α-α0=arcsin(sinα0cosθ)-α0

(10)

3.2 修正量计算

反坦克火箭筒射击时，如果不考虑横风、气温等其他影响射角和射向的因素，则横倾导致的射击偏差量改变符号后即为射击修正量[4]，所以对横倾的方向修正量∠β和高低修正量∠α分别为

∠β=-arctan(tanα0sinθ)

(11)

∠α=α0-arcsin(sinα0cosθ)

(12)

规定右倾时，θ为正值；左倾时，θ为负值

4 实例计算

假设反坦克火箭筒在横倾状态下射击，使用的弹种为破甲弹，α0分别取射击距离400、600、800 m所对应的高低射角，向右侧横倾，横倾范围：0′～300′，将α0及横倾角代入式(9)、(10)，可计算得出在不同的距离下射击时，火箭筒不同的横倾角度所引起的火箭弹方向偏差量和高低偏差量，如表1、2所示。

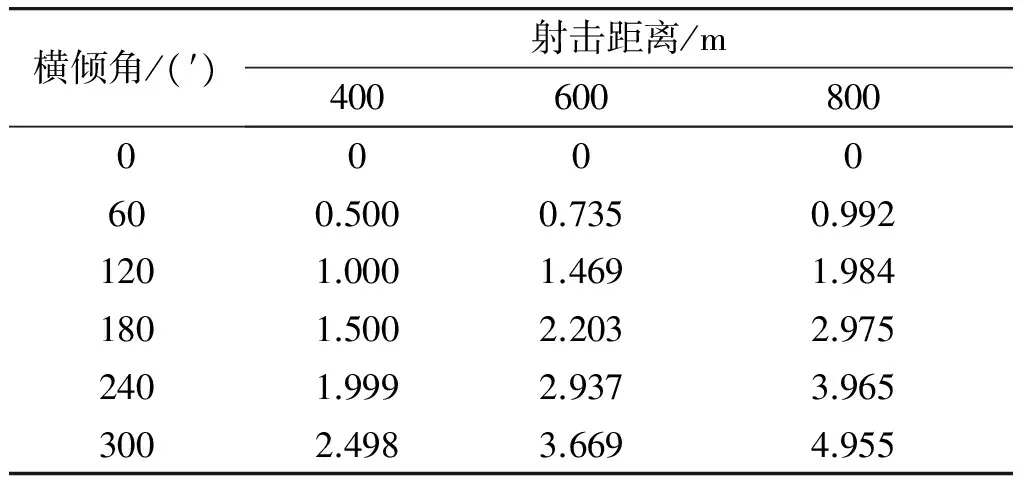
表1 不同横倾角、射击距离下的方向偏差量 密位

表2 不同横倾角、射击距离下的高低偏差量 密位

从表1、2中可以看出，反坦克火箭筒在横倾状态下射击时引起的方向和高低偏差量均会随着射击距离和横倾角的增大而增大，但是二者的数值大小相差很大。

同样的外界条件下，方向偏差量远大于高低偏差量。在400 m距离，横倾60′的情况下，方向偏差量是高低偏差量的近125倍。在800 m距离，横倾300′时，这一比值仍然达到了25倍。

从数值上看，在400～800 m的范围内，方向偏差量最小也超过了0.5密位,最大接近5密位，而高低偏差量则最大不超过0.22密位。

利用Origin软件对全射程下，反坦克火箭筒在全倾角(火控系统能够测量的横倾角度[5])范围内射击时引起的方向和高低偏差量进行分析，并用等高线图的形式显示数据的变化，其结果如图3、4所示。

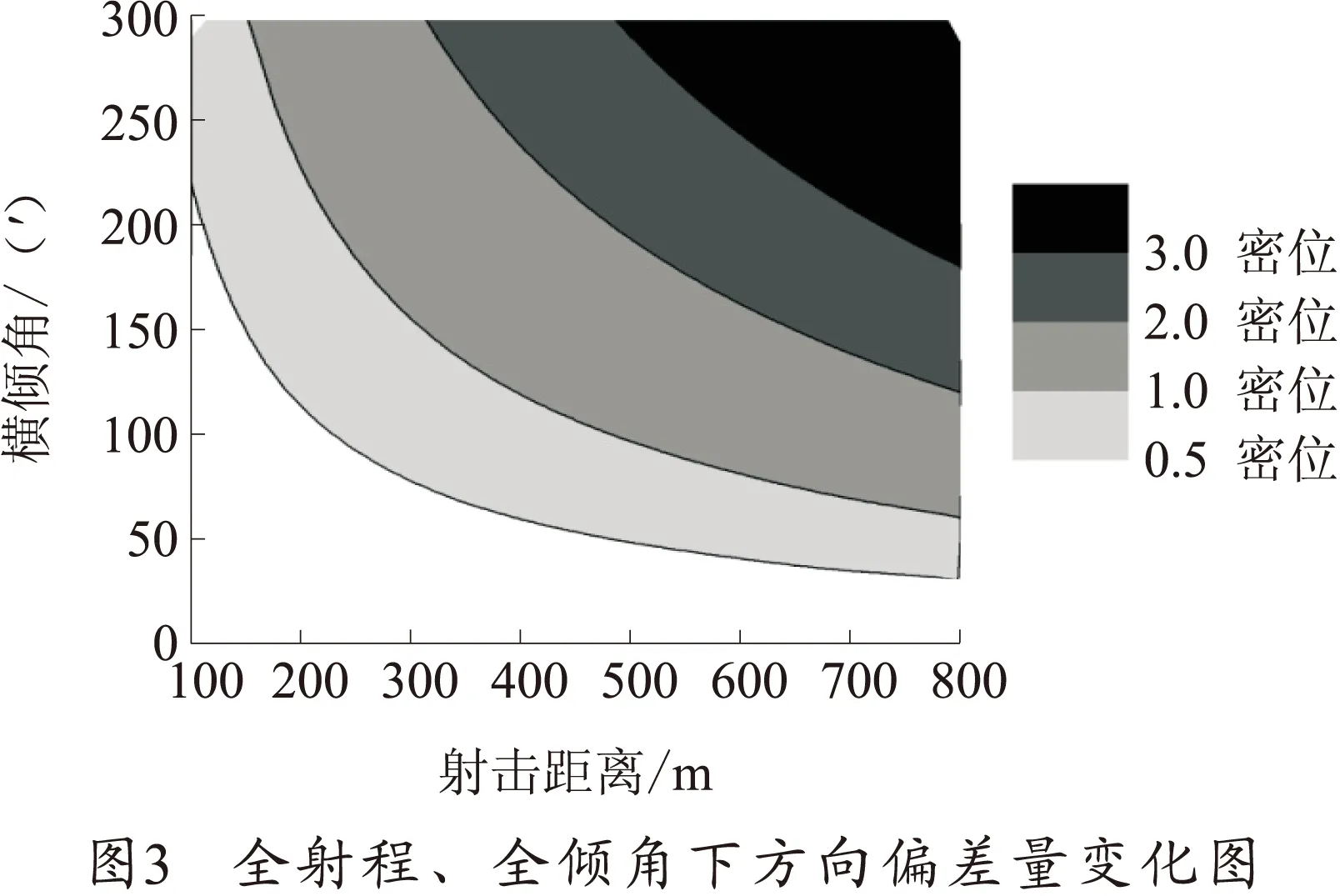
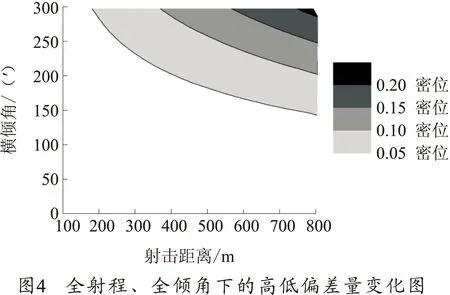
从图3、4中可以看到，在全射程、全倾角范围下，方向偏差量有超过2/3的数值大于0.5密位。而高低偏差量只有不到1/2的数值大于0.05密位，但全部数值均小于0.3密位。

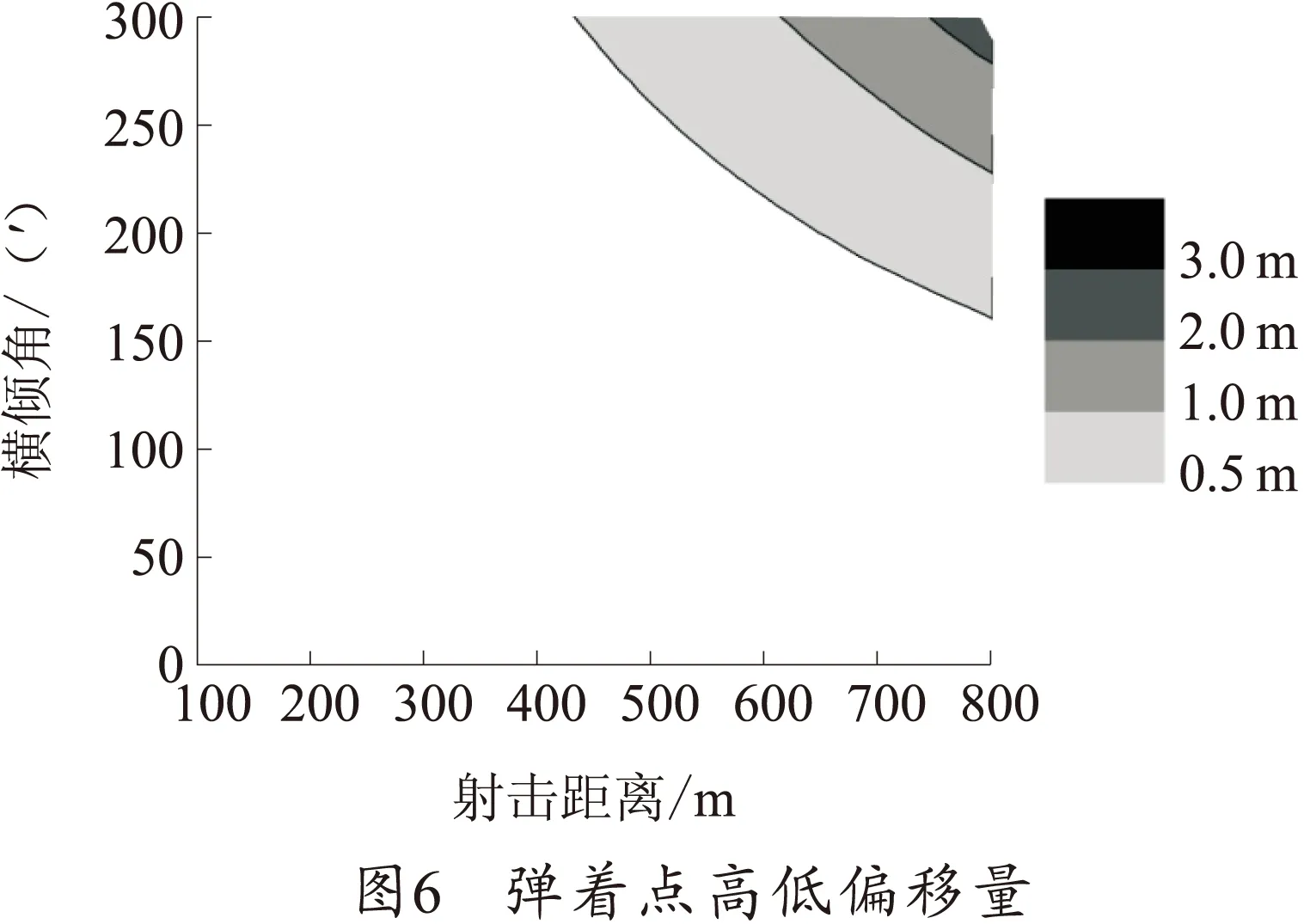
为更加清晰地显示偏差对射击精度的影响，将方向和高低偏差量换算成相应距离上的弹着点偏移量，结果如图5、6所示。

从图5可以看出，超过了1/3的弹着点方向偏移量大于0.5 m。在部分情况下，这一偏移量甚至超过了3 m。而反坦克火箭筒的典型打击目标正面尺寸仅为2 m×2 m，如果不修正方向偏差，很难命中目标，因此，必须修正横倾带来的方向偏差量。

从图6和表2可以看出，只有不到1/4的弹着点高低偏移量超过0.05 m，即便在偏差最大的情况下(800 m，300′)，其弹着点高度也仅变化0.18 m，甚至小于火控自身的射角装定误差(简易火控的最小射角装定误差为0.25密位，在该距离上引起的弹着点变化为0.2 m[6])，对火箭弹的射击精度影响很小，可以忽略不计。因此，可以不修正横倾带来的高低偏差量。

5 结论

在射击过程中，反坦克火箭筒的横向倾斜会造

成火箭弹在方向和高低两个方向上发生偏差，这两种偏差量随着射击距离和横倾角的增大而增大，但是对于火箭弹的射击精度影响程度不同。通过计算和分析表明，横倾引起的高低偏差极小，可以忽略不计。但是横倾引起的方向偏差较大，所以横倾状态下，反坦克火箭筒的火控系统可以不修正高低偏差量，但是必须修正方向偏差量。

References)

[1]崔忠旺.120反坦克火箭兵器操作与射击指挥[M]. 石家庄：石家庄机械化步兵学院，2008：12-14. CUI Zhongwang.Operation and shooting command of 120 anti-tank rocket[M]. Shijiazhuang: Shijiazhuang Mechanized Infantry Academy, 2008:12-14.(in Chinese)

[2]满文兵.营属反坦克武器[M]. 石家庄：石家庄机械化步兵学院，2014:33-35. MAN Wenbing.Anti-tank weapon for camp[M]. Shijia-zhuang: Shijiazhuang Mechanized Infantry Academy, 2014:33-35. (in Chinese)

[3]郭锡福.远程火炮武器系统射击精度分析[M].北京：国防工业出版社，2004:81-90. GUO Xifu.Analysis about shooting precision of long-distance artillery system[M].Beijing:National Defense Industry Press，2004:81-90. (in Chinese)

[4]焦方金.120毫米反坦克火箭[M]. 石家庄：石家庄机械化步兵学院，2015:33-35. JIAO Fangjin. 120 mm anti-tank rocket[M]. Shijia-zhuang: Shijiazhuang Mechanized Infantry Academy. 2014,33-35. (in Chinese)

[5]陈志坚.PF98A式120毫米反坦克火箭兵器操作与射击[M].西安：西安陆军学院，2009:27-29. CHEN Zhijian. Operation and shooting command of PF98A 120 mm anti-tank rocket[M].Xi’an：Xi’an Army Academy,2009:27-29. (in Chinese)

[6]张录. PF98/98A式120毫米反坦克火箭[M]. 石家庄：石家庄机械化步兵学院, 2014:42-46. ZHANG Lu.PF98/98A 120 mm anti-tank rocket[M]. Shijiazhuang: Shijiazhuang Mechanized Infantry Academy,2014:42-46. (in Chinese)

The Quantitative Analysis of Deviation About Rear Sight forAnti-tank Rocket on the Slope

ZHOU Yongqiang1， JIAO Fangjin2

(1.Shijiazhuang Army Command Collage, Shijiazhuang 050084，Hebei，China；2.Shijiazhuang Mechanized Infantry Academy, Shijiazhuang 050083，Hebei，China)

The shooting accuracy of the anti-tank rocket would be influenced and the shooting deviation caused if the anti-tank rocket leaned to one side. Through building up the anti-tank rocket coordinate system, describing the state of body of anti-tank rocket before or after the time when it heeled, analyzing and changing the coordinate system, mathematics model of shooting deviation could be calculated under the heeling condition. By using Origin software, the deviation in terms of direction and height was calculated on different degrees and different distances when typical bombs are used for anti-tank rocket. Through analyzing the calculating result, the deviation in terms of direction and height for heeling would become larger with the increase of the degree of slope and the distance of shooting, but the difference in affecting shooting accuracy, the deviation of height could be ignored if it were extremely small, but the deviation of direction would be corrected if it were larger. The calculating method and result can offer reference for formulating firing table accurately.

engineering mathematics；anti-tank rocket；heel；corrections

2016-06-12

周永强(1978—)，男，讲师，博士研究生，主要从事兵种战术研究。E-mail：zhouyongqiang _re@163.com

10.19323/j.issn.1673- 6524.2017.02.006

TJ301

A

1673-6524(2017)02-0025-04