基于自然连通度的复杂网络节点重要性度量方法*

沈安慰，郭基联，王卓健

（空军工程大学航空航天工程学院，西安 710038）

基于自然连通度的复杂网络节点重要性度量方法*

沈安慰，郭基联，王卓健

（空军工程大学航空航天工程学院，西安 710038）

节点重要性度量是复杂网络研究中的热点问题。从复杂网络的抗毁性指标入手，给出了自然连通度的定义，并且以此为基础设计了基于自然连通度的复杂网络节点重要性度量方法。最后以著名的风筝网络为例，分析了该方法的适用性，并与其他经典的节点重要性度量方法进行对比，证明了该方法的合理性。

复杂网络，自然连通度，风筝网络，节点重要性

0 引言

现实世界中的很多复杂系统都可以用网络来刻画。随着基础研究的不断深入，各国的研究工作者和工程技术人员逐渐认识到计算机通信网络系统、国家交通网络、社会关系网络、武器装备体系等复杂系统的研究都可以归结于复杂网络。如何判断复杂网络中节点的重要性是复杂网络研究中急需解决的关键问题之一［1］。

大量实际复杂网络的研究结果表明，分析节点的度（网络中与该节点相连的边的数量）是衡量节点重要性的一个简单有效方法。度指标描述了一个节点的邻居节点的个数，体现了该节点与周围节点之间建立直接联系的影响力。显然，网络节点的度越大，该节点越重要。但度指标只利用了自身的信息，没有考虑到该节点在网络中的位置。王建伟［2］等在度指标的基础上提出了节点及邻居节点度的概念，认为网络中节点的重要性不仅与自身的度有一定的联系，并且与该节点邻居节点的度也存在一定的关联。在此基础上，任卓明［1］等综合权衡考虑了节点的邻居个数以及其邻居之间的连接紧密程度，提出了一种基于邻居信息与集聚系数的节点重要性评价方法。

上述方法都是基于局部信息进行节点重要性度量的。此类方法算法复杂度较低，能够适应大规模复杂网络，但计算精度往往不高，难以体现网络的全局特征。基于网络全局属性的节点重要性指标研究也得到了大量的研究。例如，考虑网络邻接矩阵的特征值和特征向量的节点重要度评价方法。Sabidussi提出了描述网络节点重要性的紧密度指标，之后人们在此基础上定义了Kernel函数法。Comin考虑度与介数的关系，定义了一个新的节点重要性评价指标。此类方法较为经典，但面对大规模复杂网络时则表现出了算法复杂度较高的缺点。

另一种评价复杂网络节点重要性的思路是将该节点删除，在对删除指定节点后复杂网络特性研究的基础上进行评估。例如，李鹏翔［3］认为删除节点的重要性可以用该节点被删除后形成的所有节点之间的最短距离的倒数之和来度量。谭跃进［4］在此基础上提出了一种评估复杂网络节点重要度的节点收缩方法。饶育萍［5］认为网络平均等效距离越多，网络的抗毁能力越强，并提出了一种基于平均等效最短路径数的抗毁评价模型，认为如果节点失效后网络抗毁度下降得越多，则该节点在网络中的重要性越大。此类方法在指定网络中表现较好。

针对上述复杂网络节点重要性度量方法的不足和优点，本文从复杂网络抗毁性指标入手，提出了基于复杂网络自然连通度的节点重要性度量方法。并将其与常见的度量方法进行对比分析，证明了本文所提方法的合理性。

1 节点重要性度量的常用方法

定义1：简单无权图G中，若vi与vj之间存在边则aij=1，否则aij=0，且aii=0。则称为网络的邻接矩阵。

1.1 节点度

节点的度为与该节点相连接的邻居节点数目。具体可表示为

节点度指标能够直观地反映一个节点在网络中的重要程度。例如，在朋友关系网络中，一个人拥有的朋友越多，在网络中就越重要。

1.2 节点及其邻居节点度

在节点度的基础上，研究者［2］又提出了节点及其邻居节点度方法来判断一个节点的重要程度。即节点的度以及节点的邻居节点的度越大，节点就越重要。该方法认为连接节点的边越重要，节点就越重要。具体可表示为：

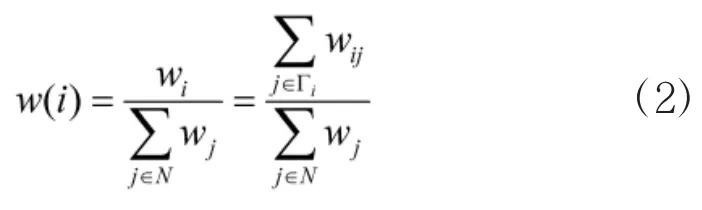
其中，wi表示节点i所连边的权值之和，wij表示边ij的权重，且。。A为邻接矩阵，e为单位向量。

1.3 度与集聚系数

任卓明［1］等人综合考虑节点的邻居个数，以及其邻居之间的连接紧密程度，又提出了度与集聚系数的节点重要度评估方法。该方法利用节点的邻居信息，并考虑节点邻居之间的紧密程度，节点重要性评价指标pi表示为

1.4 紧密度

度量网络中节点重要程度的另一种方法是度量该节点通过网络对其他节点施加影响的能力，可用紧密度来表示，具体如下：

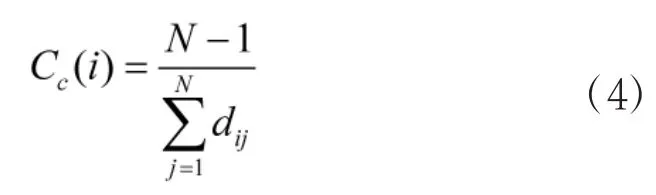
其中，dij表示节点i到节点j的最短距离。

1.5 Kernel函数法

考虑节点的影响范围，一些学者又定义了Kernel函数法，具体如下：

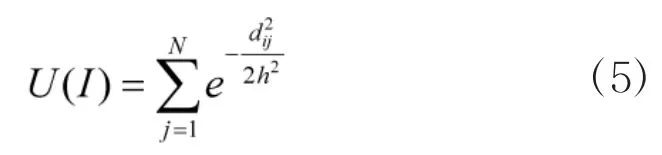
其中，dij表示节点i到节点j的最短距离，h表示Kernel函数的宽度。h越大表示此函数越平滑，因此，节点的影响范围也越大。

2 基于自然连通度的复杂网络节点重要性度量

2.1 理论基础

复杂网络节点重要性度量可借助网络的抗毁性指标来表征。并且认为如果节点失效后网络抗毁度下降得越多，则该节点在网络中的重要性越大。本文在饶育萍［5］的基础上，考虑抗毁性指标新的测度方法——自然连通度，以此来评价网络中节点的重要性。

现实网络可能节点众多、连接复杂，传统基于图论的抗毁性测度已不适用于复杂网络的抗毁性度量。本文关注到吴俊［6-7］等人提到以自然连通度为测度衡量复杂网络抗毁性。分析发现，自然连通度在描述网络抗毁性时其计算复杂度很低而精确性很高。

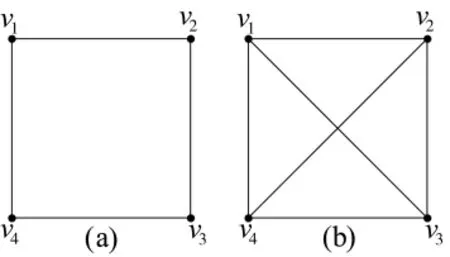
图1 简单网络示意图

自然连通度从网络的冗余替代路径出发描述一个网络的抗毁能力。我们知道，网络的抗毁能力与节点之间的冗余替代路径密切相关。例如，图1是由4个节点构成的简单网络示意图。图1（a）和图1（b）中节点v1到节点v4的路径数如表1所示。显然，图1（b）的网络抗毁性能强于图1（a）所示的网络。通过这样一个简单案例，可以看出，网络抗毁性源于网络中节点冗余替代路径的数目。

表1 图1（a）、图1（b）节点到节点的路径数

由于复杂网络一般冗余替代路径计算和完全统计非常困难，那么可以换种思路，统计网络中所有封闭路径冗余数（网络中从一个节点出发经过若干其他节点最后仍能够回到出发节点的所有路径统称为封闭路径），这样同样能够表示网络的抗毁性能。设nk表示一个网络所有路径长度为k的封闭路径数，S表示所有封闭路径数，那么有

S的值越大，表明网络中冗余替代路径数目越多，其抗毁性越好。考虑到统计网络中长度为k的路径数时存在大量重复统计。如长度为2的路径共统计了2次，长度为3的路径共统计6次。因此，S可按式（7）计算

由于当N较大时S值也很大，所以考虑简化

S*表示网络特征谱密度平均值的自然对数，由此可定义S*为网络的自然连通度，i是网络邻接矩阵的特征值，N是网络节点数。

若G为无向图，则A（G）为对称矩阵，即aij=aji。令为A（G）的特征根，则集合｛｝i为图G的邻接矩阵特征谱。

自然连通度从网络中的内部结构属性出发，通过计算网络中不同长度闭环数目的加权和，刻画了网络中替代途径的冗余性，具有明确的物理意义和简洁的数学形式。文献［6-7］在详细阐述自然连通度提出的背景意义基础上，推导了自然连通度和邻接矩阵特征值的关系，并证明了其关于添加节点或边是严格单调的，获得了国际学术界的高度认可。因为自然连通度能精确地刻画出复杂网络的抗毁性细微区别，准确表征出抗毁性的演化过程，并且相对来讲具有便于计算的特点，所以本文以自然连通度为基础，探索复杂网络节点重要性度量的新方法。

2.2 方法步骤

本文以复杂网络的自然连通度为基础，设计了基于自然连通度参数的节点重要性度量方法，具体步骤如下：

步骤3：按照节点的顺序依次删除网络中的每一个节点与其对应的连边。每删除一个节点，其邻接矩阵为，计算该状态下网络的自然连通度，共可得到N个自然连通度。

从上述步骤可以看出，节点的重要度pi表征的物理意义在于节点删除之后，网络抗毁性改变的快慢的趋势。

3 案例分析

以Krackhardt设计的“风筝网络”为例［8］，分析本文提出的基于自然连通度的复杂网络节点重要性度量方法。风筝网络的结构如图2所示。

首先将该网络表示为邻接矩阵的形式，如表2所示。

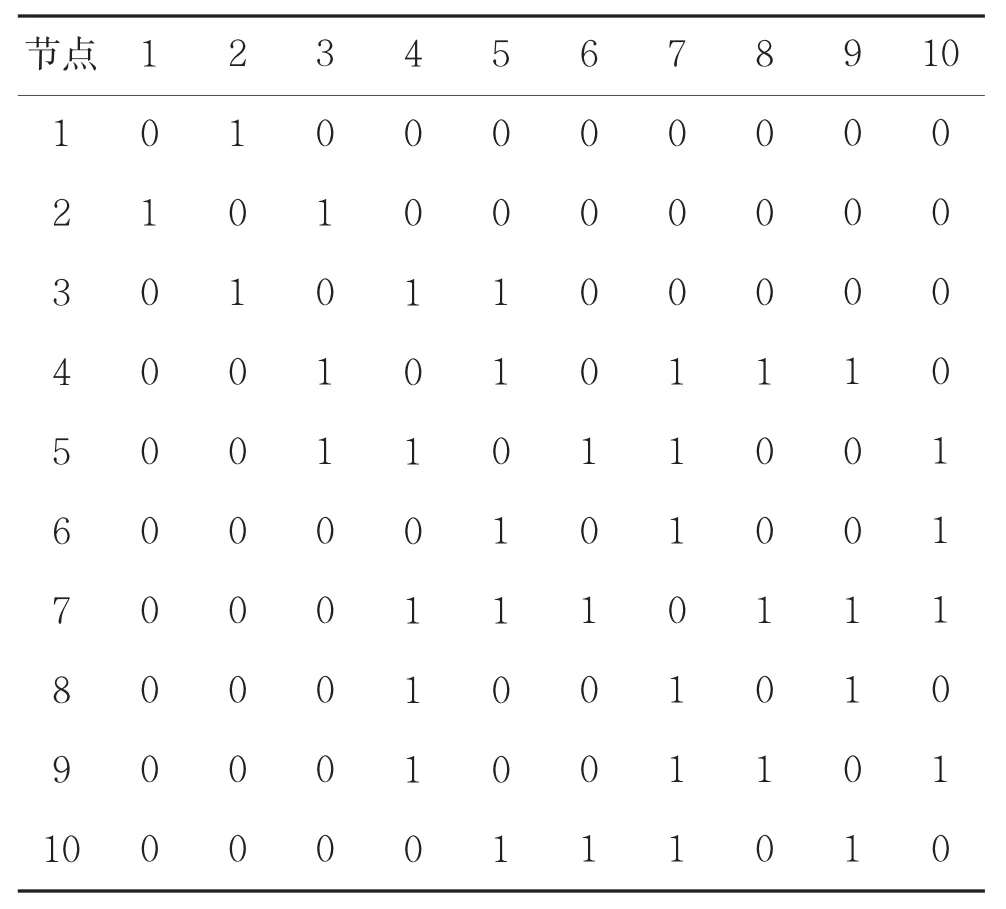
表2 风筝网络的邻接矩阵

表3 风筝网络节点重要性度量结果

从表3中可以看出，风筝网络中基于自然连通度的复杂网络节点重要性排序为，表明节点7在风筝网络中最为重要，节点1最为不重要。该计算结果与节点度、节点及其邻居节点度、Kernel函数法的计算结果一致。但节点度、节点及其邻居节点度在某些情况下不能区分部分节点的重要性排序，这两种方法度量结果较为粗糙。

图2 风筝网络

基于度与集聚系数的方法在节点3的重要性认定上与本文的方法出现了不一致的现象，主要是由于该方法考虑了聚类系数。在高聚集性网络中，其节点重要性评估的效果会有所降低。

基于紧密度的方法也在节点3的认定上与本文方法出现了不一致的现象，主要是该方法认为节点3被破坏了之后整个网络就出现了不连通现象。

从上述各种方法的对比可以看出，基于不同的度量标准，网络节点重要性的度量结果就会不一样。本文从复杂网络的抗毁性入手，提出的基于自然连通度的节点重要性度量方法具有一定的现实意义。

4 结论

节点重要性度量的侧重点不同，其结果自然不一样。本文以复杂网络抗毁性为重要性度量标准，提出了基于自然连通度的复杂网络节点重要性度量方法，并且给出了该方法的计算步骤。最后，本文以风筝网络为例，分析了本文方法的节点重要性度量结果，并与经典方法进行对比分析，证明了本文所提方法的合理性。

［1］任卓明，邵凤，刘建国，等.基于度与集聚系数的网络节点重要性度量方法研究［J］.物理学报，2013，62（12）：128901.

［2］王建伟，荣莉莉，郭天柱.一种基于局部特征的网络节点重要性度量方法［J］.大连理工大学学报，2010，50（5）：822-826.

［3］李鹏翔，任玉晴，席酉民.网络节点（集）重要性的一种度量指标［J］.系统工程，2014，22（4）：13-20.

［4］谭跃进，吴俊，邓宏钟.复杂网络中节点重要度评估的节点收缩方法［J］.系统工程理论与实践，2006，26（4）：79-83.

［5］饶育萍，林竞焉，月东方.网络抗毁度和节点重要性评价方法［J］.计算机工程，2009，35（6）：14-16.

［6］WU J，BARAHONA M，TAN Y J，et al.Spectral measure of structural robustness in compex network ［J］，IEEE Transactions on Systems Man and Cybernetics Part A ，2011，41（6）：1244-1252.

［7］WU J，BARAHONA M，TAN Y J，et al.Natural connectivity of complex network［J］.Chin Phys Lett，2010，7（7）：078902.

［8］汪小帆，李翔，陈关荣.网络科学导论［M］.北京：高等教育出版社，2012.

［9］袁荣坤，孟相如，李明迅，等.节点重要度的网络抗毁性评估方法［J］.火力与指挥控制，2012，37（10）：40-42.

Research of Complex Networks Node Importance Ranking Based on Natural Connectivity

SHEN An-wei，GUO Ji-lian，WANG Zhuo-jian
（School of Aeronautics and Astronautics Engineering，Air Force University of Engineering，Xi’an 710038，China）

Node importance ranking of complex networks is a hot topic nowadays.This paper gives the definition of natural connectivity.And then the method of complex networks node importance ranking based on natural connectivity has been proposed.Finally，the applicability of proposed method is analyzed by an example of kite network.The contrast of proposed method and other common method prove that the reasonability of our method.

complex networks，natural connectivity，kite network，node importance

TP399

A

1002-0640（2017）05-0052-04

2016-03-17

2016-06-17

国家自然科学基金资助项目（71501185）

沈安慰（1988- ），男，浙江衢州人，在读博士研究生。研究方向：飞机RMS论证与评估。