从波利亚的解题步刍谈高中学生解数学题的常见错误及应对策略

云南省曲靖师范学院(655011)

梁金华●

从波利亚的解题步刍谈高中学生解数学题的常见错误及应对策略

云南省曲靖师范学院(655011)

梁金华●

防止和避免解题错误是提高学生数学成绩的有效方法.文章结合波利亚的解题步骤讨论了高中学生在数学解题过程中出现的各种错误，并对其原因进行了深入分析，最后提出应对的策略．

解题错误；理解；方法；过程；反思

美籍匈牙利数学家G·波利亚在《怎样解题》中，把数学问题解题步骤分为四个环节，第一，读清楚题意；第二，题目给出的已知条件之间的联系，已知条件和要求的问题之间又有什么关系，确定解题的方法；第三，根据解题方法进入解题过程环节；第四，回顾与检查所完成的解题过程，确保答案的正确．结合高中生在数学学习中的实际情况，在数学解题中出现的错误大体分为四类：题意理解的错误、解题方法的错误、解题过程的错误、检查与反思的错误．

一、题意理解的错误

不理解题意是目前高中生数学解题错误的一个重要原因，主要包括概念的理解错误，忽视了公式、定理、法则成立的条件；隐含条件的挖掘不充分．

1.概念理解错误

概念本身比较抽象，若不进行深入学习和正反例的对比，不理解本质很容易犯错．

2.忽视了公式、定理、法则成立的条件

如果在学习公式、定理、法则时，只是把公式死记住而没有真正理解本质，就容易忽视它们成立的条件．

3.隐含条件的挖掘不充分

隐含条件通常涵盖在某个数学概念中，有时隐含在几何图形的特殊位置上，有时隐含在知识间的联系中．在解题的过程中，不把隐含条件全部挖掘出来，很容易导致解题出错．

在本例中有一个隐含条件：方程有两根，这就要求Δ≥0．没有挖掘到这一条件，就很容易给出错误的答案．

二、解题方法的错误

在高中数学解题过程中，找到解题的策略对于快速准确的解题来说是最重要也是最困难的一步．选定解题方法是解答题目过程中的重要环节，它关系到整个问题解决的成败.常见的解题方法错误类型有：分类讨论不当，类比不当，不善于从整体解答，缺乏“正难则反”策略．

1.分类讨论不当

分类不当，常常表现为以偏概全，忽略特例，从而导致解题错误．

例4 有11个工人，其中5个青年工人是钳工，另有4个青年工人是车工，还有两个师傅既能当钳工，也能当车工，现在要在这11个工人里选4名钳工，4名车工修理一台机器，问有多少种选派方法？

在本题中，有同学做了如下分类：(1)两个师傅都作钳工；(2)两个老师傅都当车工；(3)两个老师傅中，一人作钳工，另一人作车工．但是三种情况不是相互独立的，而是既有重复部分，也有遗漏部分．由于偶然的巧合，一重一漏却使结果与正确解法的结果相同，但这不能说明解法是正确的．正确的分法应该是(1)两个师傅都不在内；(2)两个老师傅都当车工；(3)两个老师傅都当钳工；(4)两个老师傅中，一人当钳工，另一人当车工；(5)两个老师傅中，一人当钳工，另一人不参加选派；(6)两个老师傅中，一人当车工，另一人不参加选派．

2.类比不当.

在数学解题中，由两种知识或技能的某些相似，推出他们的其他属性也可能相同或相似的思维形式就是类比．恰当的类比可以简化问题，而不恰当的类比往往会产生解的错漏．

一些同学看到题目马上会想到通过求导得到曲线在某点处的切线斜率．但却犯了一个类比上的错误：在某点处的切线方程不同于过某点的切线方程，在某点处的切线方程切点就是该点，切线仅有一条；但过某点的切线方程切点不一定是该点，方程也不一定只有一条．

3.不善于从整体解答

有的数学题，从整体才能看出问题的全貌，才能更深刻地分析问题的特征．考虑从整体解题是从全方面思考问题的一种指导思想，重点在于整体把握，不仅仅是局限于细节方面，这样可以排除次要因素的干扰．而部分学生往往习惯性地从局部出发，而不善于从整体考虑，从而使问题复杂化，而且可能解答不出问题，也会导致解题错误．

代入上式，得M=194.

4.缺乏“正难则反”的策略

一些数学问题，从正面解决不容易，可以从反面去思考.当用直接求解法解答不出时，就采用间接求解法;当问题从正面证明不了，则采用反证法.这种对数学问题正面解答有困难反过来从反面寻求答案的方法就是“正难则反”的策略．

本题如果从正面，设h1,h2,h3的判别式Δ1,Δ2,Δ3，这样由已知条件会有七中情况，运算量很大，计算非常困难．但若是从反面考虑，即考虑h1,h2,h3的图象中没一个与x轴相交，这样就只有一种情况：

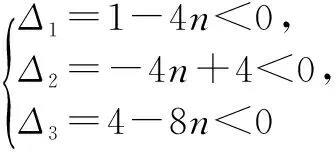
最后就可以知道题目的答案为n≤1．

三、解题过程错误

解题过程是在找到解题策略之后重要的一步，通过表述解题过程再次检验解题方法正确性.如果解题可以顺利完成，说明解题方法是正确的；如果不能解出题目，或解题过程困难很大，说明解题方法不完善或者有问题，这时就要重新思考解题方法，选择合理的方法来解，这个过程需要多次重复才可以完成．解题过程中常见的错误有：不等价转换，循环论证．

1.不等价转换

在高中数学解题过程中，需要将问题的已知条件加以转换．这个转换必须是已知条件的充要条件，用已知条件的充分条件代替已知条件，就可能出现失解；而用已知条件的必要条件代替已知条件，就有可能产生增解．

这道题有同学是这么做的：

①

②

可是最显然取x=0符合解集的要求，却不能使原题不等式成立.产生错误的根源是能使①式成立的x必然能使②式成立，但能使②式成立的x却不一定能使①式成立，二者是不等价转换.

2.循环论证

在证明题中，论题由论据来推出，如果论据又由论题本身推出，这实际上就是论题由论题本身推出，称为循环论证．一个循环论证并没有真正完成要证明的论题．

例8 在直角三角形ABC中，∠C=90°，AB=c,BC=a,AC=b．证明：a2+b2=c2．

如果设a=csinA，b=ccosA，

由sin2A+cos2A=1

得a2+b2=c2sin2A+c2cos2A=c2，

即证a2+b2=c2．

这样的证明是有问题的，sin2A+cos2A=1这一结论成立的条件就是勾股定理的一种特殊情况，把它当成了已知条件来使用，最终导致了循环论证的错误．

四、检查与反思的错误

把数学题解答完后进一步的检查与反思是确认答案正确的一种方案，也是解题过程中必不可少的步骤．做完题目的检查是数学解题整个过程的最后一步，这一步对于数学解题来说也是很关键的．由于在审题、解题、表述的过程中，难免会出现一些错误，所以结果不一定就是正确答案，为了确保最后答案的准确，则需要我们做完题目时进行检查，以便及时发现错误，改正错误．在数学解题中，由于不注重检验，功亏一篑的现象时有发生，它要求我们要时刻注意检查，千万不要掉以轻心．比起审题和解题方法的确定，检查的环节是很多学生最不关注的，波利亚将其作为解题的必要环节固定下来，是一个有远见的做法．

有些同学是这样做的：

方程两边乘以x(x-2)消去分母，得(x-2)+3x=-2，

从而解得x=0．

可是如果把x=0代入原方程验证就会发现出错：x=0不能做分母，该方程无解．

避免或减少数学解题过程中错误的发生是老师和学生共同的目标．而有效地控制错误，减少错误的策略可提高数学解题的能力.面对学生可能犯的形形色色的错误，教师要能正确看待，不要一味地批评和指责，须知“失败乃成功之母”．更要从学生的解题错误反省自己的教学．通常，容易出错的地方都是各章节的教学重难点和关键之处，教师应深入剖析出错的原因．只有找出错误的根源，才能让学生进一步去学习新知识．发现学生解题的错误时，老师不要急着去纠正，可以带着学生一起寻找错误的根源．在必要的时候，可以结合学生所犯的错误，搜集一些类似的题目，举一反三，让学生针对所犯的错误加以练习，让学生从正、反两方面比较，深刻理解，减少或者避免类似错误的出现，达到纠错的目的．还可以针对学生常犯的错误，在课堂上设置纠错情境，引起学生注意.引导学生分析错误原因，寻找改错的“良药”，在知错中改，改错中防，以弥补学生在知识上的不足和思维上的缺陷，增加解题的准确性，思维的严谨性，从而提高数学解题能力．也可以利用学生的作业、课堂练习、口头回答问题中常见的错误，设计引起争论的问题或者创设一些处于学生模糊观念之间的纠错情境，这样既能与学生的实际紧密结合又能激起学生的学习兴趣，促使学生主动思考．

对于学生的解题错误，我们要防，要避．如果避不开，也要充分发挥教师自身的教育机智，对错误的合理性加以利用，尽可能去发现学生在错题中的闪光点，因势利导，引导学生寻找错误的根源，激发他们解题的兴趣，让他们感受成功之后的喜悦，从而提高学习的积极性．

G632

B

1008-0333(2017)01-0033-02