试题是怎样炼成的
——一类基于合情推理的圆锥曲线试题命制
2017-06-15福建省泉州第五中学362000
福建省泉州第五中学(362000)
杨苍洲●
试题是怎样炼成的
——一类基于合情推理的圆锥曲线试题命制
福建省泉州第五中学(362000)
杨苍洲●
合情推理有“归纳”和“类比”两种推理模式,这种推理是建立在观察、实验的基础上,通过“类比”来产生“联想”,或者通过“归纳”来进行“猜想”,是一种“发现未知”的思维形式.
在解析几何的某些问题中,我们常常可以通过类比、归纳,从中发现“圆、椭圆、双曲线、抛物线”的一些共同性质.因此,基于“圆锥曲线”,交汇考查“合情推理”成为命制“解析几何”试题的一种常见命题手法.这样的试题设计精彩纷呈,往往成为一份试卷的亮点所在.下面笔者略举数例,与读者共赏.

(Ⅰ)求轨迹C的方程;


分析与解 本小题主要考查抛物线的定义与标准方程、直线与圆锥曲线的位置关系等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、数形结合思想、特殊与一般思想等.
(Ⅰ)易得曲线C的方程为y2=4x.
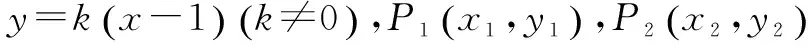
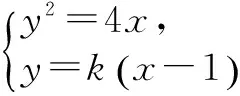


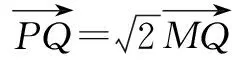
(Ⅰ)求曲线Γ的方程;


分析与解 本小题主要考查圆的方程与性质、椭圆的标准方程与性质、直线与圆锥曲线的位置关系等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、数形结合思想、特殊与一般思想等.
(Ⅱ)设三角板的直角顶点放置在圆O的圆周上的点N(a,b)处,则a2+b2=2,又设三角板的另一条直角边所在直线为l′.
(ⅰ)当a=1时,l′与曲线Γ有且只有一个公共点.
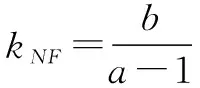

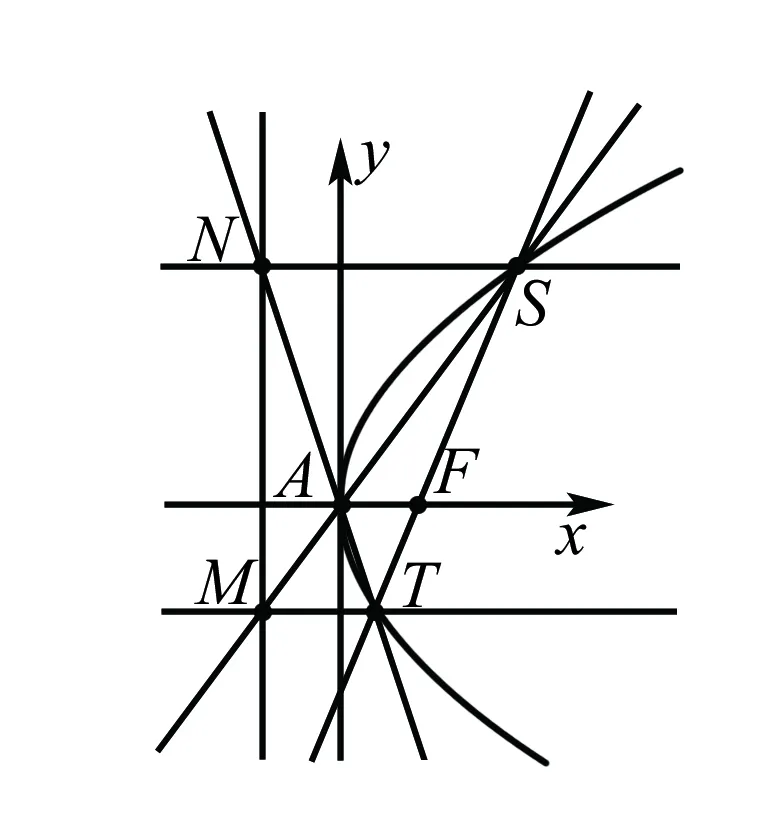
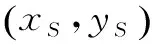
(Ⅰ)拖动点S,发现当xS=4时,yS=4,试求抛物线E的方程;
(Ⅱ)设抛物线E的顶点为A,焦点为F,构造直线SF交抛物线E于不同两点S、T,构造直线AS、AT分别交准线于M、N两点,构造直线MT、NS.经观察得:沿着抛物线E,无论怎样拖动点S,恒有MT∥NS.请你证明这一结论.

分析与解 本小题主要考查抛物线的标准方程、直线与圆锥曲线的位置关系等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、分类与整合思想、数形结合思想等.
(Ⅰ)易得抛物线E的方程y2=4x.

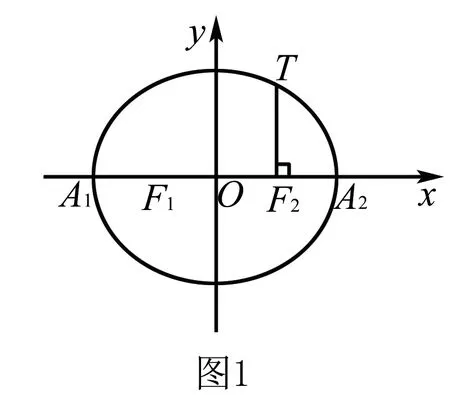

(Ⅰ)求椭圆E的方程;
(Ⅱ)给出命题:“已知P是椭圆E上异于A1,A2的一点,直线A1P,A2P分别交直线l:x=t(t为常数)于不同两点M、N,点Q在直线l上.若直线PQ与椭圆E有且只有一个公共点P,则Q为线段MN的中点”,写出此命题的逆命题,判断你所写出的命题的真假,并加以证明;
(Ⅲ)试研究(Ⅱ)的结论,根据你的研究心得,在图2中作出与该双曲线有且只有一个公共点S的直线m,并写出作图步骤(注意:所作的直线不能与双曲线的渐近线平行) .
分析与解 本小题主要考查椭圆的标准方程与性质、直线与圆锥曲线的位置关系等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、数形结合思想、特殊与一般思想等.

(Ⅱ)逆命题:“已知P是椭圆E上一点,直线A1P、A2P分别交直线l:x=t(t为常数)于M、N两点,若Q为线段MN的中点,则直线PQ与椭圆E有且只有一个公共点P”,为真命题.

(Ⅲ)如图,①任作一条直线n垂直于实轴;②作直线A1S、A2S分别交直线n于I、J两点;③作线段IJ的中点V,则直线SV即为所求的直线m.
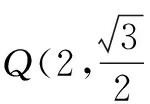
(Ⅰ)求双曲线C的方程;
(Ⅲ)试推广(Ⅱ)中的命题,写出关于圆锥曲线(椭圆、双曲线、抛物线)统一的一般性命题(不必证明).
分析与解 本小题主要考查合情推理、直线、椭圆、双曲线、抛物线等基础知识,考查推理论证能力、运算求解能力,考查数形结合思想、化归与转化思想、特殊与一般思想.
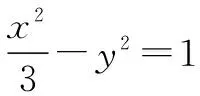
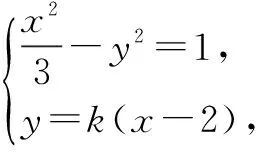

上述几个试题的求解过程,要求学生经历逆向思维、类比推理、直观感知、操作确认、思辨论证,度量计算的心路历程.虽然试题情境新颖,但是其本质依然是研究曲线轨迹,求解直线与抛物线位置关系等问题.因此在复习中,我们要深化对圆锥曲线方程的理解,进一步熟练掌握待定系数法、定义法等求轨迹的常规方法,进一步掌握直线与抛物线位置关系的一般解题方法,要注意总结试题的规律,如:直线与圆锥曲线位置关系中的相交弦问题在高考中经常被设计成考题,在解决此类问题时,我们常联立方程组,利用韦达定理,进行“设而不解”来解题.
G632
B
1008-0333(2017)01-0028-03
