函数图象在高中数学解题中的应用
2017-06-15湖南省长沙市麓山滨江实验学校410000
湖南省长沙市麓山滨江实验学校(410000)
刘佳伟●
函数图象在高中数学解题中的应用
湖南省长沙市麓山滨江实验学校(410000)
刘佳伟●
函数在高中数学中占据着非常重要的地位,函数的数形结合的思想也是高中数学学习大纲中必须掌握的一个重要思想.函数图象在高中函数学习中的运用其实是非常普遍的,其目的主要是提高解题速度和解题的准确性.本文主要就自己的切身经验谈谈关于函数图象在高中数学解题中的应用的一些看法.
函数图象;高中数学;函数学习
函数图象与数学解题之间其实是存在着非常微妙的联系,函数图象在很多情况下使得数量关系和立体的空间得以巧妙地结合,并且往往我们还能从这种结合的图象中思索观察出题目问题的解决方法.在高中的数学学习中,实际的解题经验会教会我们,将函数作为解析的主要过程,往往能够在很多情况下把较为复杂难解的问题简单化.
一、函数图象在数学选择题解题中的运用
1.判断函数的零点
在判断函数的零点以及有几个零点这类的题目中,函数图象往往能够在解题中起到很大的作用.
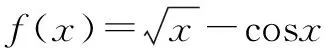
A.没有零点 B.有且仅有一个零点
C.有且仅有两个零点 D.有无穷多个零点
2.在指定区间内判断方程的根的个数
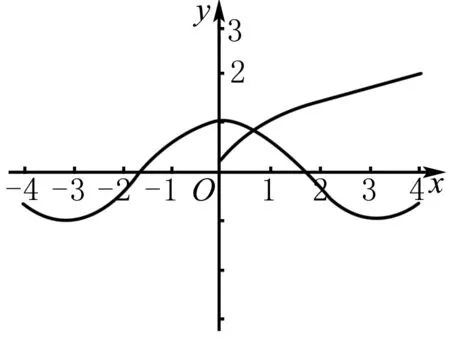
例2 方程2x+x3-2=0在区间(0,1)内的实根个数是( ).
A.0 B.1 C.2 D.3
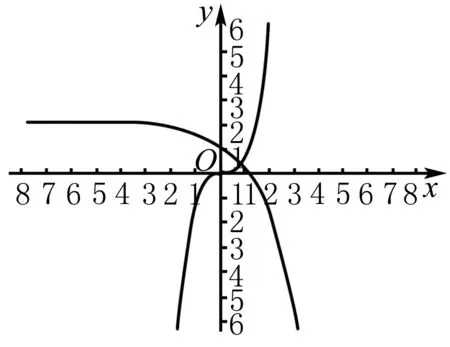
解法 1.将题目中的方程2x+x3-2=0拆分成为两个函数f(x)=2-2x,g(x)=x3,这样再根据两个拆分函数图象就可以很直观地根据它们的交点的个数来判断出在区间(0,1)内的零点个数,如图,也就是说在区间(0,1)内原函数的零点个数只有1个.
3.利用函数图象比较大小
例3 若loga2 A.1 C.0 解析 ∵loga2 ∵loga2 ∴a>b.∴0 含参数方程是指方程的系数没有确定,要根据方程根的分布去判断参数的范围.这样的题目小题、答题都有,但是一般都会和其它的知识点综合比如不等式、数列等. 例4 关于x的实系数方程x2-ax+2b=0的一个根在区间[0,1]上,另一个根在区间[1,2]上,则2a+3b的最大值为____. 画出可行域,可求得目标函数z=2a+3b的最大值是9. 二分法是指利用区间两端对应的函数值异号,就可以得知该区间内就必有实数根,通过计算区间中点对应的函数值,然后将区间一分为二,将函数值为异号的区间继续进行二分,直至达到精准的要求. 例5 求方程lgx=3-x的近似解(精确度0.1). 原方程为x+lgx-3=0,令f(x)=x+lgx-3,可用计算器得f(2)≈-0.70,f(3)≈0.48,于是f(2)f(3)<0,所以这个方程在区间(2,3)内有一个解.用二分法,取区间(2,3)中点2.5,f(2.5)≈-0.10,再取区间(2.5,3)的中点,2.75 ,f(2.75)≈0.19,f(2.5)f(2.75)<0,所以x0∈(2.5,2.75).同理可得x0∈(2.5,2.625),x0∈(2.5625,2.625).由于2.625-2.5625=0.0625< 0.1,所以原方程的近似解可取为2.5625. 其实函数图象在高中数学解题中的应用是非常广泛的,有时候它能够很有效地提升我们的解题速度,但是前提是作为学生,我们必须要掌握各种函数的基本性质,对于函数的相关模型有充分的理解,并且在能够多做相关的练习题进行针对性的练习,平时要多加思考. [1]李玉莲.函数图象在高中数学解题中的应用[J].数理化学习:高三版, 2015(6):54-54. [2]邹丽丽.函数与方程思想在高中数学解题中的应用[J].高中数理化, 2014(22):6-6. [3]王鹏.浅谈数形结合思想在有关高中数学解题中的应用——以函数和集合为例[J]. 商情, 2015:254-255. G632 B 1008-0333(2017)01-0042-01二、函数图象在含参数方程中的运用

三、利用函数图象结合二分法求方程的近似解
