火星进入段自适应预测校正制导方法

李毛毛，胡 军

(北京控制工程研究所，北京100190)

火星进入段自适应预测校正制导方法

李毛毛，胡 军

(北京控制工程研究所，北京100190)

针对火星进入段预测制导收敛性和可解性问题，给出基于一阶特征模型的全系数自适应预测校正制导律。该方法首先通过时变动态增益变换技术大幅度降低预测误差与制导修正量之间的时变动态增益；然后对变换后的系统建立修正量与广义航程误差间的一阶特征模型，应用全系数自适应方法估计一阶特征模型系数并求取制导修正量；再由标称制导剖面和制导修正量确定纵向制导输出，横向制导采用传统的漏斗边界制导方法。本文方法每个制导周期仅执行一次预测制导，依靠自适应控制的逐次逼近实现制导的收敛性，避免了基于迭代的传统预测校正制导方法的收敛性问题。针对预测校正制导收敛性这一国际上的难题，本文首次证明了全系数自适应预测校正制导律的收敛性。最后针对火星进入点多种初始误差的组合，以及火星大气密度和探测器气动参数的偏差，进行了多条轨迹的仿真。结果表明，全系数自适应预测校正制导具有较高的精度，在计算时间上也要优于基于迭代的预测校正制导方案，更加适合在工程上的应用。

火星进入段制导; 全系数自适应；预测校正；组合误差仿真

0 引 言

神舟飞船、嫦娥系统以及天宫系列任务的相继成功，标志着我国载人航天等相关领域的技术已经达到了国际的领先水平[1]，目前我国针对深空探测的研究也越来越多,作为距离地球最近的行星之一，火星在很多方面都与地球相似，因此成为人类进行深空探测的重要目标天体之一[2-3]。由于火星大气层非常稀薄，整个进入过程经历的时间短，状态变化快，对减速性能的要求很高。火星大气具有很大的不确定性，时常出现狂风、沙尘等天气；考虑到火星的大气密度仅为地球大气的1%，相对地球再入，火星进入一般选择比地球再入更大的进入角和更短的进入航程，以弥补火星进入气动力不足的影响。相较于飞船返回地球，较弱的控制能力和参数的不确定性，对制导方法的要求更高，因此具备一定自适应能力的制导方法，已经成为国内外火星探测领域的研究热点[4 -7]。

进入段制导方法一般分为跟踪标称轨迹的制导方法和基于落点预报的预测校正制导方法[8-10]。在跟踪标称轨迹制导方面，为了提高算法的精度，一是研究具备鲁棒性能和自适应能力的弹道跟踪方法，二是研究在线弹道规划算法[11-14]，但依然没从根本上解决标准轨道制导方法固有的对参数变化敏感和操作灵活性差的问题。

预测校正制导方法实时动态规划弹道[15],能从根本上解决标准轨道制导方法对初始再入条件敏感和操作灵活性差的问题。文献[16]提出了一种基于阻力加速度的预测-校正制导方法，采用插值的阻力加速度剖面对过程约束具有更强的处理能力。李惠峰等[17-18]将预测校正方法应用到低升阻比，RLV以及探月飞船返回中，算法对初始误差有较好的鲁棒性，能应付各种不确定性的影响，扩宽了预测校正法的使用范围。由于动力学参数相对标称参数的变化直接导致预测结果的误差，常规的预测校正制导方法对动力学参数相对标称参数的变化同样也是敏感的，必须对动力学等价实现的气动参数或/和气动综合因子在线实时估计并补偿，自适应的预测校正制导方法可以实现更高的制导精度和更高自主能力[19-22]。

数值预测校正制导方法之前受制于计算机处理速度，如今随着宇航级计算机的快速发展，为数值预测校正制导方法工程上的应用提供基础。国外和国内绝大多数的预测校正制导方法研究，校正部分采用多次迭代的数学寻优方法，对本身是非线性时变含大范围不确定性的系统，校正的收敛性问题没有解决，在一些初始条件下存在不收敛现象，制导计算开销不确定，难以在工程上利用[23-25]。

胡军提出的全系数自适应预测校正制导方法，分为两步：1)通过发现的预测校正模型时变动态增益的变化规律，对预测校正模型构造标称状态下的时变动态增益变换，大幅降低预测校正模型的时变增益；2)对变换后的系统，建立输出与输入之间的一阶特征模型，估计一阶特征模型的系数，实时求取自适应制导修正量。该算法不需要迭代过程，在很大程度上减少了机载计算机的负担，使算法更有实际意义[21]，该方法已经在航天实际飞行任务中得到验证[26-27]。

传统的预测校正制导方法，通过数值迭代方法得到校正量，算法的收敛性一直是学者关心的问题，当前最可靠的算法是迭代单一参数的数值算法[28-29]。本文全数值自适应预测校正制导方法，将制导这样的两点边值问题转化为标准的输入-输出控制问题，因此算法收敛性的证明可以借鉴控制问题的思路。基于此，本文证明了全系数自适应预测校正制导律的稳定性，不同于文献[30]中具有保守性的区间时变系统的稳定性证明，本文将一阶特征模型看成一种特殊的线性时变系统，通过证明全系数自适应预测校正制导律的稳定性，保证了预测校正制导法的收敛性，对工程上的可靠应用给出了理论基础。

本文针对火星进入段初始点等各种组合误差进行仿真校验，结果表明全系数自适应预测校正制导具有较高的精度，在计算时间上也优于基于迭代的预测校正制导方案，更加适合在工程上的应用。

1 火星进入段制导问题的建立

1.1 火星进入段动力学模型

本文采用如下的大气进入段模型：

(1)

式中：

r为探测器到火星球体中心的距离，θ为探测器经度，φ为探测器纬度；v为探测器速度;γ为探测器航迹倾角，为探测器与当地水平面的夹角;ψ为探测器航迹方位角，为当地北极与探测器飞行速度在当地水平面投影的夹角;σ为倾侧角，为探测器绕着速度轴旋转的角度，即升力与当地垂线的夹角；L、D分别为升力加速度和阻力加速度:

g为探测器的重力加速度，g=μ/r2；ρ为火星大气密度，采用标准指数型大气密度模型，ρ=ρsexp(-β(r-rs))，ρs为探测器在高度rs处的大气密度；CL、CD为探测器的升力系数和阻力系数，S为探测器的参考表面积，m为探测器的质量，B为探测器的弹道系数，B=m/CDS。

1.2 火星探测器纵程、横程、航程的相关定义

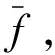
航程是火星探测器质心与火星球心连线在球面上的交点走过的距离，可以通过积分下面的微分方程得到

(2)

式中：s为火星探测器航程。

待飞航程是由飞行器当前经纬度和期望终端点的经纬度决定的。由球面三角形的知识可以得到待飞航程为

stogo= arccos[sinφcsinφs+

cosφccosφscos(θc-θs)]

(3)

式中：φc、θc表示火星探测器当前点的经纬度，φs、θs表示期望终端点的经纬度。

侧向制导中用到横程定义为

z=arcsin[sinstogosinΔψ]

(4)

式中：Δψ=ψ-Ψ为火星探测器的航迹方位角ψ与探测器视线方位角Ψ的差值，由球面三角形的知识，可以得到视线方位角Ψ为

sinΨ=[sin(θc-θs)cosφc]/sinstogo

(5)

2 火星进入段制导方法

2.1 火星进入段自适应全数值预测校正法

实际飞行中，一个制导周期内利用式(1)～(5)预报当前制导策略下探测器的实际落点，计算出探测器的航程相关量。实际落点和期望落点之间存在纵程误差和横程误差，自适应全数值预测校正制导方法根据误差对制导律进行修正，本质上是积分型制导算法，是一种闭环无差系统，把误差的修正均匀分布到当前点到终端时刻的整个区间内，通过不断的预报与修正，最终将火星探测器导引到预定的落点[21-22]。

校正环节根据航程差计算出纵向升力特征量的增量，就需知道纵向升力特征量的改变量与航程改变的关系。从标称开伞时刻往前度量，如果倾侧角改变的越早，相同的改变量下，对航程影响就会越大。另外升力特征量的增量对航程的改变，还与当时的飞行状态，气动参数等有关。下面研究一种特殊情形：升力特征量的增量加入之前，火星探测器一直处于标称飞行状态。虽说是一种特殊情形，但是从中可以看出修正量和误差之间的特征关系[22]，航程误差随时间单调变化，即修正量加入越早，对航程改变越大。图1～2分别为升力特征量的增量为0.1和-0.1时航程的改变量。

定义 1. 预测的航程误差与纵向升力特征量的变化量之比定义为时变动态增益D(t)。

通过分析，纵向升力特征量的修正量u(k)与预测误差y(k)之间的关系用一阶变系数差分方程表示如下，相对之前采用的二阶模型，辨识参数更少，对系统变换的适应性更快，制导精度也更高[20-21]：

y(k+1)=f(k)y(k)+g(k)u(k)

(6)

式中：y(k)表示相对期望终端点的落点航程误差，u(k)表示倾侧角的修正量。

制导律设计中，利用梯度法辨识特征模型系数f(k)和g(k)，定义回归向量为

α(k)=[y(k-1),u(k-1)]T

(7)

需要估计的参数向量为

β(k)=[f(k),g(k)]T

(8)

(9)

式中：λ1和λ2为正的常数。

该方法相对传统的预测校正方法，不进行迭代制导，每个制导周期只进行一次自适应控制计算，辨识参数后，采用线性反馈控制得到倾侧角的修正量

(10)

式中：L是控制器参数，一般选取大于0的数，λ与系统的参数g(k)同号。

因为采用的是积分型制导算法，还需通过积分器的作用，得到最新的倾侧角值。经过不断的预测校正，最终引导火星探测器到达期望的落点，图4为制导流程图。

注1.上面所述是探测器的纵向制导，横向制导是倾侧角的正弦起作用，如果倾侧角的取值过小或者过大，留给侧向的控制能力很有限，所以控制量需要留有一定的余量，对u(k)和积分后总的倾侧角控制量都有上下限的约束。

2.2 火星进入段横向制导方法

本文中火星进入段制导方法采用纵横向解耦的方法进行控制,将侧向航程的误差边界设计成以侧向速度为自变量的漏斗形，当碰到漏斗边界的时候，倾侧角符号反向。

2.3 自适应全数值预测校正法稳定性分析

基于迭代的预测校正制导法存在的一大问题是校正环节算法的收敛性，这也是目前该算法只停留在理论研究而没有在实际工程中利用的一个原因。本文提到的自适应全数值预测校正法，将制导问题转化用一阶特征模型表示的时变动态系统的控制问题，是标准的输入-输出系统，因此自适应全数值预测校正法收敛性的证明可以借鉴控制问题稳定性证明的思路。

自适应全数值预测校正法通过不断的预测校正，依靠自适应控制的逐次逼近实现制导的收敛性，下文首次证明了全系数自适应预测校正制导律的收敛性问题。

工程应用中，特征模型的参数在特定的取值范围内，即

(11)

用梯度法辨识特征模型参数的时候，经过投影算子，将参数估计值投影到式(11)的范围内。当系统的采样时间T确定时，上述参数范围可以变换为如下形式

(12)

将控制律(10)代入特征模型(6)，可得闭环系统

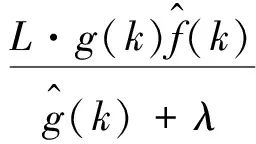
(13)

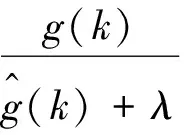
(14)

如果取λ=kλgmin，其中kλ>0，结合式(12)，易得

(15)

为了进行稳定性分析，将式(13)改写为如下形式

y(k+1)=A0(k)y(k)+Aξ(k)y(k)

(16)

式中：

A0(k)=1-L·G(k)

(17)

根据式(16)，首先分析y(k+1)=A0(k)y(k)的稳定性。

引理 1[31-32].对于线性时变系统x(k+1)=A(k)x(k)，A(k)∈Rp×p，设A(k)，k≥0满足下列两个条件：

1)δ

2)M

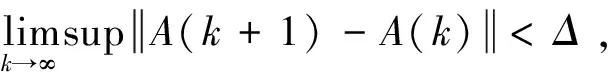
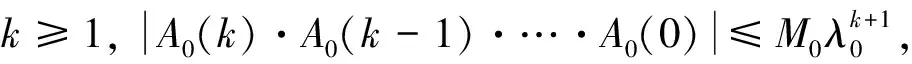
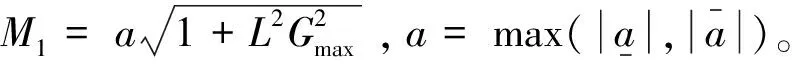
(18)

(19)

得到

定义q=M0M1T/λ0,根据Bellman-Gronwall不等式[31]，令Bellman-Gronwall公式中

可得

(20)

由等比数列求和公式可得

(21)

令T*=(1-λ0)/2M0M1,当T

(22)

将式(21)代入式(20)，得到

(23)

因为0<λ0<1，所以0<(λ0+1)/2<1，于是可以得出闭环系统(13)是指数稳定的，定理1得证。

根据定理1的结论，如注2选取L、kλ，自适应全数值预测校正法在每一次预测校正制导周期，由式(10)给出倾侧角的修正量，将预测误差值分布到余下的时间段内。随着特征模型组成的闭环系统的稳定性，保证了自适应全数值预测校正法的收敛性。

3 仿真校验

为了校验上述所提方法的有效性，首先对火星进入段自适应全数值预测校正法进行校验，进入点的初始值和误差范围大小如表1所示。图5～10为各种误差组合下火星探测器的状态量和控制量随时间变化的仿真图。从图6～8可以看出，在各种误差作用下，探测器仍然可以很好地到达开伞点高度，落点经纬度也都达到了很好的精度。图5表示多条轨迹的倾侧角控制量，倾侧角都在一个有限的范围内，比较平滑，这样留有一定的余量，在遇到干扰或者误差比较大的情况时还有较大的机动能力。经过几个制导周期，落点航程误差可以很快地收敛，趋近于0，制导效果很好。

注3.Lu[28]提出的预测校正方法，校正环节通过迭代方法(比如牛顿迭代法，有界试位法等)迭代得到消除偏差或者偏差足够小的修正指令，具体方法可以参考文献[28-29]。

在本节中，对两种制导方法进行了对比，对大气密度，升力系数和阻力系数进行组合拉偏，仿真结果如表2所示。两种制导方法都可以达到较高的精度，自适应全数值预测校正法总体上的制导精度要比迭代校正的数值预测校正法高，最大的落点误差未超过1.5km。

表1 进入点初始状态及误差范围Table 1 Initial states and dispersion ranges

表2 进入点初始误差及参数偏差下的仿真结果Table 2 The simulation results with Initial dispersion and parameter dispersion

图11和图12分别为初始误差都取最大值时，自适应预测校正制导律和迭代预测校正制导律的倾侧角仿真图。从图11～12可以看出，自适应预测校正的倾侧角比迭代预测校正的倾侧角更为平滑，而且倾侧角也留有一定余量，这样针对干扰的控制能力更强，减少了探测器控制的负担。另外在制导末端时间段，自适应预测校正制导律的倾侧角归零，为开伞创造了条件，更符合实际工程情况。

最后，本节还对两种制导方法的算法仿真时间进行了对比，在同样的仿真硬件和软件条件下，自适应预测校正制导律的仿真时间明显比迭代的预测校正方法要快。以最大误差条件下的仿真为例，利用MATLAB仿真，自适应预测校正制导律的仿真时间为0.35s，迭代的预测校正制导律为1.13s。

综上所述，自适应预测校正制导律比迭代的预测校正制导律更加适合用于火星进入段的制导。针对各种初始误差，火星大气密度，探测器气动系数的不确定性，都有很好的鲁棒性；而且算法时间也有优势，能够很好地在工程上实现。

4 结 论

针对火星进入段制导问题，在神舟飞船再入制导的基础上，本文给出了基于一阶特征模型的自适应预测校正制导方案，横向沿用漏斗边界的方案，并和国外基于数值迭代的预测校正方法进行了对比，创新性地证明了全系数自适应预测校正制导律的收敛性，是对之前技术的发展和完善。在理论基础上，针对各种初始误差，对大气密度和气动参数进行了拉偏处理。由仿真结果可知，基于一阶特征模型的自适应预测校正制导具有较高的精度，在计算时间上也要优于基于迭代的预测校正制导方案，倾侧角策略也更加合理，为工程利用提供了依据。

[1] 欧阳自远，李春来，邹永廖，等. 深空探测的进展与我国深空探测的发展战略[J]. 中国航天，2002(12)：28-32. [Ou-yang Zi-yuan, Li Chun-lai，Zou Yong-liao, et al. Progress of deep space exploration and Chinese deep space exploration strategy [J]. Aerospace China, 2002 (12): 28-32.]

[2] Scheeres D J. Interactions between ground-based and autonomous navigation for precision landing at small soler-system bodies[R].Telecommunications and Data Acquisition Progress Report, 1998:42-132.

[3] 李爽，彭玉明，陆宇平. 火星EDL导航制导与控制技术综述与展望[J]. 宇航学报, 2010, 31(3):621-627. [Li Shuang, Peng Yu-ming, Lu Yu-ping. Review and prospect of Mars EDL navigation guidance and control technologies [J]. Journal of Astronautics, 2010, 31(3): 621-627.]

[4] 王大轶，郭敏文. 航天器大气进入过程制导方法综述[J]. 宇航学报，2015, 36(1)：1-8. [Wang Da-yi, Guo Min-wen. Review of spacecraft entry guidance [J]. Journal of Astronautics, 2015, 36(1): 1-8.]

[5] Braun R D, Manning R M. Mars exploration entry, descent and landing challenges [J]. Journal of Spacecraft and Rockets, 2007, 44(2)： 310-323.

[6] Topcu U, Casoliva J, Mease K D. Minimum-fuel powered descent for Mars pinpoint landing [J]. Journal of Spacecraft and Rocktes, 2007, 44(2): 324-331.

[7] Shen H, Seywald H, Powell R W. Desensitizing the minimum-fuel powered descent for Mars pinpoint landing [J]. Journal of Guidance, Control and Dynamics, 2010, 33(1): 108-115.

[8] Leavitt J A, Mease K D. Feasible trajectory generation for atmospheric entry guidance [J]. Journal of Guidance, Control and Dynamics, 2007, 30(2): 473-481.

[9] Thorp N A, Pierson B L. Robust roll modulation guidance for aeroassisted Mars mission [J]. Journal of Guidance, Control, and Dynamics, 1995, 18(2): 298-305.

[10] Dierlam T A. Entry vehicle performance analysis and atmospheric guidance algorithm for precision landing on Mars [D]. Cambridge: Massachusetts Institute of Technology, 1990.

[11] 李昭莹，张冉，李惠峰. RLV轨迹在线重构与动态逆控制跟踪 [J]. 宇航学报，2015，36(2):196-202. [Li Zhao-ying, Zhang Ran, Li Hui-feng. On-board trajectory reconfiguration and dynamic inverse tracking control of RLV [J]. Journal of Astronautics, 2015，36(2): 196-202.]

[12] Lu P. Regulation about time-varying trajectories: precision entry guidance illustrated [J]. Journal of Guidance, Control, and Dynamics, 1999, 22(6): 784-790.

[13] Benito J, Mease K D. Nonlinear predictive controller for drag tracking in entry guidance[C]. AIAA/AAS Astrodynamics Specialist Conference and Exhibit, USA, August, 2008.

[14] Restrepo C, Valasek J. Structured adaptive model inversion controller for Mars atmospheric flight [J]. Journal of Guidance, Control, and Dynamics, 2008, 31(4):937-957.

[15] 赵汉元. 飞行器再入动力学和制导[M]. 长沙：国防科技大学出版社，1997.

[16] 王涛，张洪波，朱如意，等. 考虑阻力加速度的再入预测—校正制导算法[J]. 宇航学报，2017，38(2):143-151. [Wang Tao, Zhang Hong-bo, Zhu Ru-yi, et al. Predictor-corrector reentry guidance based on drag acceleration [J]. Journal of Astronautics, 2017, 38(2): 143-151.]

[17] 李惠峰，凌源. 基于预测校正法的低升阻比飞船再入轨迹设计[J]. 北京航空航天大学学报，2009，35(6):705-708. [Li Hui-feng, Ling Yuan. Reentry trajectory design of low lift-to-drag(L/D) ratio spacecraft based on predictor-corrector method [J]. Journal of Beijing University of Aeronautics and Astronautics, 2009,35(6): 705-708.]

[18] 李惠峰，张蕊. 探月飞船预测—校正再入制导律设计[J]. 空间控制技术与应用，2009，35(1): 19-24. [Li Hui-feng, Zhang Rui. Design of predictor-corrector reentry guidance law for lunar mission spacecraft [J]. Aerospace Control and Application, 2009，35(1): 19-24.]

[19] 胡军，张钊. 数值预测校正制导方法用于大升阻比再入飞行器的研究[C].中国自动化大会，武汉, 中国,2015年11月27-29日.[Hu Jun, Zhang Zhao．A study on the numerical predictive guidance method for reentry vehicle with large lift drag ratio[C]. China Automation Conference ,Wuhan, China， November 27-29, 2015.]

[20] 胡军. 基于预测的全系数自适应校正采用一阶特征模型的论证[R].北京：北京控制工程研究所报告，2014. [Hu Jun. Demonstration and proof of a first order characteristic model applied to prediction-based all-coefficient self-adaptive corrector[R]. Beijing: Beijing Institute of Control Engineering Report,2014.]

[21] 胡军. 载人飞船的一种混合再入制导方法[J]. 航天控制, 1999, 17(2):19-24. [Hu Jun. A kind of mixed reentry guidance method for manned spacecraft [J]. Aerospace Control, 1999, 17(2): 19-24.]

[22] 吴宏鑫，胡军，解永春. 基于特征模型的智能自适应控制[M]. 北京：中国科学技术出版社，2009.

[23] Zhang Zhao, Hu Jun. Prediction-based guidance algorithm for high-lift reentry vehicles [J]. Science China: Information Sciences, 2011, 54(3): 498-510.

[24] 王希季. 航天器进入与返回技术[M]. 北京：宇航出版社，1991.

[25] 胡军. 载人飞船全系数自适应再入升力控制[J]. 宇航学报, 1998, 19(1): 8-12. [Hu Jun. All coefficients adaptive reentry lifting control of manned spacecraft [J]. Journal of Astronautics, 1998, 19(1): 8-12.]

[26] 胡军，张钊.载人登月飞行器高速返回再入制导技术研究[J].控制理论与应用, 2014, 31(12):1678-1685. [Hu Jun, Zhang Zhao. A study on the reentry guidance for a manned lunar return vehicle [J]. Control Theory & Applications, 2014, 31(12): 1678-1685.]

[27] 叶培建，杨孟飞，彭兢，等. 中国深空探测进入/再入返回技术的发展现状和展望[J].中国科学：技术科学，2015，45(3):229-238. [Ye Pei-jian, Yang Meng-fei, Peng Jing, et al. Review and prospect of atmospheric entry and reentry technology of China deep space exploration [J]. Science China: Technology Sciences, 2015，45(3): 229-238.]

[28] Brunner C W, Lu P. Skip entry trajectory planning and guidance [J]. Journal of Guidance, Control and Dynamics, 2008, 31(5): 1210-1219.

[29] Lu P. Entry guidance, a unified method [J]. Journal of Guidance, Control and Dynamics, 2014, 37(3): 1-39.

[30] 张钊，胡军. 高超声速飞行器基于特征模型的自适应姿控系统稳定性分析[J]. 中国科学：信息科学，2012, 42(3)： 379-394. [Zhang Zhao, Hu Jun. Stability analysis of a hypersonic vehicle controlled by the characteristic model based adaptive controller [J]. Science China: Information Sciences, 2012, 42(3): 379-394.]

[31] 郭雷. 时变随机系统-稳定性，估计和控制[M]. 长春：吉林科学技术出版社，1992.

[32] 姜甜甜. 几类非线性不确定性系统基于特征模型自适应控制的稳定性研究[R]. 北京：北京控制工程研究所，2015. [Jiang Tian-tian. Stability analysis of adaptive control based characteristic model for a class of uncertain nonlinear systems[R]. Beijing: Beijing Institute of Control Engineering, 2015.]

通信地址：北京市海淀区中关村南三街16号(100190)

电话：(010)68378682

E-mail: limaobuaa@163.com

(编辑：牛苗苗)

An Adaptive Predictor-Corrector Method of Mars Entry Phase

LI Mao-mao, HU Jun

(Beijing Institute of Control Engineering, Beijing 100190，China)

Aiming at the convergence and solvability problems of Mars entry guidance, the all-coefficient adaptive predictor-corrector guidance method based on the first order characteristic model is proposed. The first step, the time-varying dynamic gain transformation technology is used, reducing the time-varying dynamic gain between predictor error and the guidance increment substantially. The second step, the first order characteristic model which describes the relationship between guidance increment and the error of generalized predictive range is established. The coefficients of characteristic model are estimated with all-coefficient adaptive method, and then the guidance increment is obtained. The output of longitudinal guidance concludes the nominal guidance quantity and the guidance increment. The traditional classical funnel bank angle reversal method is used for the lateral guidance. The above predictor-corrector guidance is executed only once during a guidance period. The convergence of guidance is guaranteed by the successive approximation of adaptive control, so the convergence problem of conventional predictor-corrector guidance based on iteration method is avoided effectively. Aiming at the international problem of predictor-corrector guidance′s convergence, the convergence of the all-coefficient adaptive predictor-corrector guidance method is proved for the first time. Finally, numerical simulation is done with different initial errors, the deviation of Mars′ atmosphere density and aerodynamic parameters of Mars explorer. The results show that the all-coefficient adaptive predictor-corrector guidance method has higher accuracy than the predictor-corrector guidance method based on numerical iteration, and the time of algorithm is shorter. Consequently, the proposed all-coefficient adaptive predictor-corrector guidance method is more suitable for engineering applications.

Mars entry guidance; All-coefficient adaptive；Predictor-corrector； Simulation with combined error

2017-01-17;

2017-03-16

国家自然科学基金(61333008)

V448

A

1000-1328(2017)05-0506-10

10.3873/j.issn.1000-1328.2017.05.009

李毛毛(1989-)，男，博士生，主要从事航天器导航制导与控制，飞行器再入制导与控制的研究。