相依项目反应数据的Copula建模法
2017-06-13付志慧刘罗曼孟祥斌
付志慧,刘罗曼,孟祥斌
(1.沈阳师范大学数学与系统科学学院,辽宁 沈阳 110034;2.东北师范大学数学与统计学院,吉林 长春 130024;3.东北师范大学教育学部,吉林 长春 130024)
相依项目反应数据的Copula建模法
付志慧1,2,刘罗曼1,孟祥斌3
(1.沈阳师范大学数学与系统科学学院,辽宁 沈阳 110034;2.东北师范大学数学与统计学院,吉林 长春 130024;3.东北师范大学教育学部,吉林 长春 130024)
与经典教育测量方法相比,基于项目反应理论(IRT)的教育统计与心理测量技术呈现出愈来愈多的优势.将Copula方法引入到IRT中来分析相依反应数据,对题目的边际反应概率和题目反应间的相依结构分别建模,更好地解决了项目局部相依性问题.
项目反应模型;局部相依性;Copula函数
0 引言
项目反应理论(Item Response Theory,IRT)的核心是根据被试能力与被试者对测验项目正确回答概率之间的关系建模,最常见的二级评分模型为Logistic(2PL)模型和正态卵形模型.标准的IRT模型一般建立在局部独立性假设之下,而局部独立性是指给定被试能力,同一被试在不同项目间的作答相互独立(被试在不同题上答对概率只与被试能力有关,而与其他因素无关).[1-2]以二参数Logistic模型为例,假设被试p对项目i的反应数据为ypi,取值为0或1,则二值变量Ypi取值为ypi的概率为
其中θp为被试的能力参数,αi与βi分别为题目的区分度参数和难度参数.将Ypi转换为连续潜在变量Xpi,其中Xpi服从尺度参数为1、位置参数为αi(θp-βi)的Logistic分布,[7]即
Xpi=αi(θp-βi)+pi.
(1)
令Yp为被试p在I个题目上的反应向量,则由局部独立性假设有
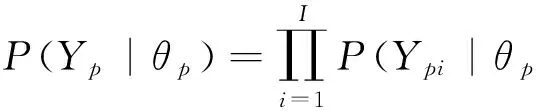
局部独立性假设在实际中有时难以满足.例如,当测验中有些项目共用同一材料或刺激(阅读短文、图、表等)时,这些项目集称为题组,显然当测验存在题组(多个项目共用同一刺激)时,同一题组内的项目间难以满足局部独立性假设.若此时仍用标准的IRT模型,会使参数的估计值有较大的误差.[3-5]在我国的考试与测评中,许多测验或量表中均有题组类型的项目,如汉语考试和外语考试中的阅读理解题、完形填空题、听力短文理解题,人才测评中的情景判断测验题以及数学试卷中的计算题等,同一题目中的不同子问题之间都是具有相关性的.因此在实际测验问题中,如何合理的对题组项目反应数据建模成为关键问题.目前有一种解决方案是建立包含交互效应的模型(CCI方法)[6],简单起见,取区分度参数αi=1,则有
反应变量Yp1和Yp2之间的相关性通过参数λ来表达.当λ=0时,上述模型退化为局部独立性模型,利用联合反应概率,可求得项目1的边际反应概率为
易见当λ≠0,即题目1与2之间存在相关性时,题目1的边际反应概率不再是2PL模型(1),边际分布函数也不再是Logistic函数.因此CCI方法的局限性在于边的不可复制性,此时β失去了原有模型中作为位置参数的解释意义,题目1的边际反应概率还要依赖于题目2的参数β2以及参数λ.其他的一些方法如题组反应模型法[8]和条件模型法[9]也会出现上述问题.
本文采用Copula方法.Copula理论要追溯到1959年,Sklar指出可以将一个K维联合分布分解成K个边缘分布和一个Copula函数,这个Copula函数描述了变量间的相关性.此方法对于边际反应概率和相依结构进行分别建模,克服了边际反应模型不可复制的问题.
1 Copula简介
定义[10]N元Copula函数是指具有如下性质的函数:
(1) 定义域为IN,即[0,1]N;
(2)C(·,…,·)有零基面且是N维递增的;
(3)C的边缘分布Cn(un),n=1,2,…,N,满足Cn(un)=C(1,…,1,un,1,…,1)=un,其中un∈[0,1],n=1,2,…,N.
显然,若F1(·),F2(·),…,FN(·)是连续的一元分布函数,令un=Fn(xn),n=1,2,…,N,则C(u1,u2,…,uN)是一个边缘分布服从[0,1]均匀分布的多元分布函数.其具有以下性质:
(Ⅰ) ∀un,vn∈[0,1],n=1,2,…,N,均有
(Ⅱ)
(Ⅲ) 若变量un∈[0,1](n=1,2,…,N)相互独立,用C⊥表示独立变量的Copula函数,则
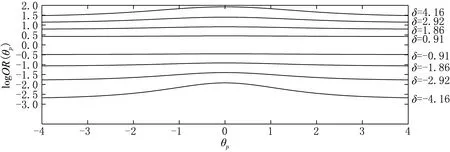
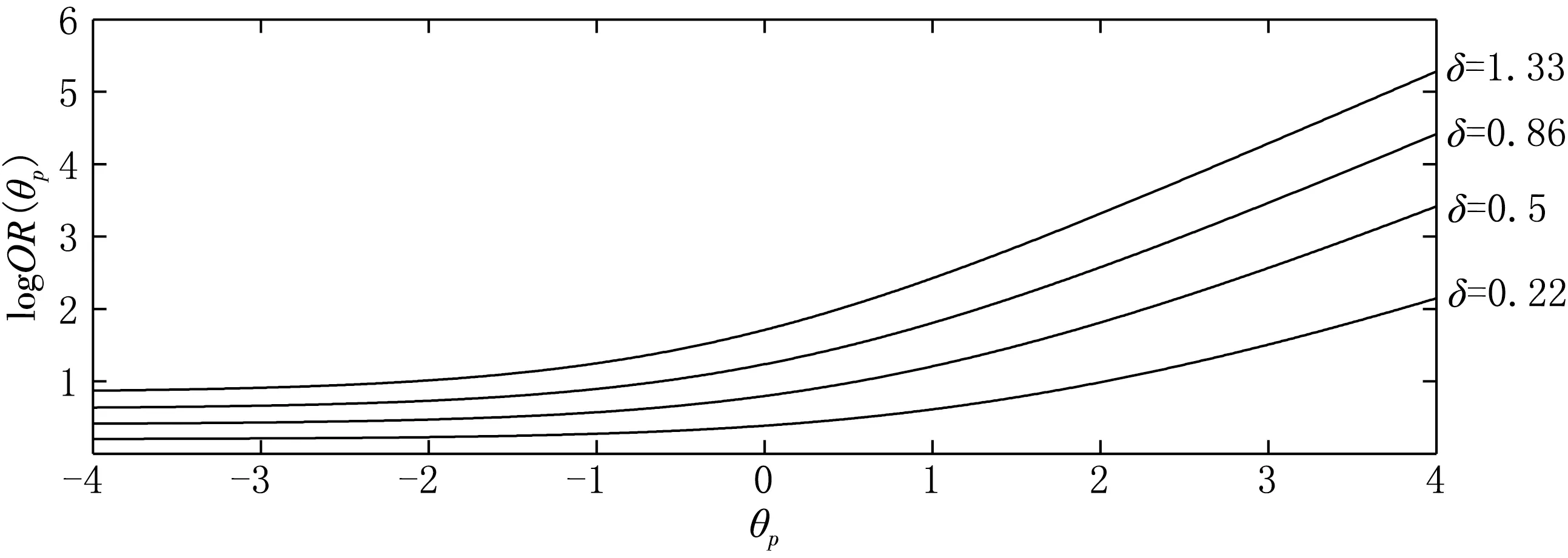
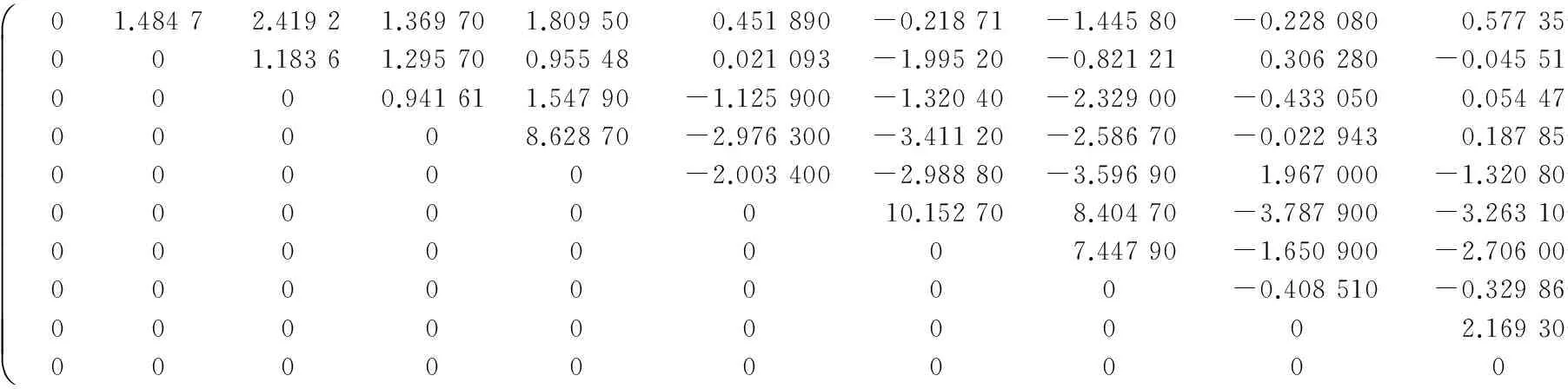
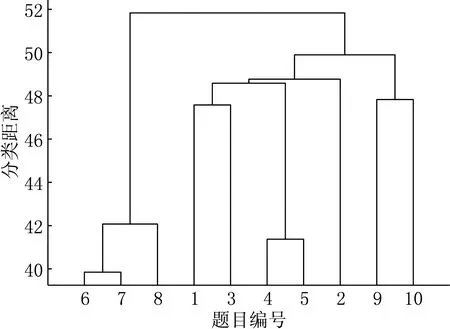
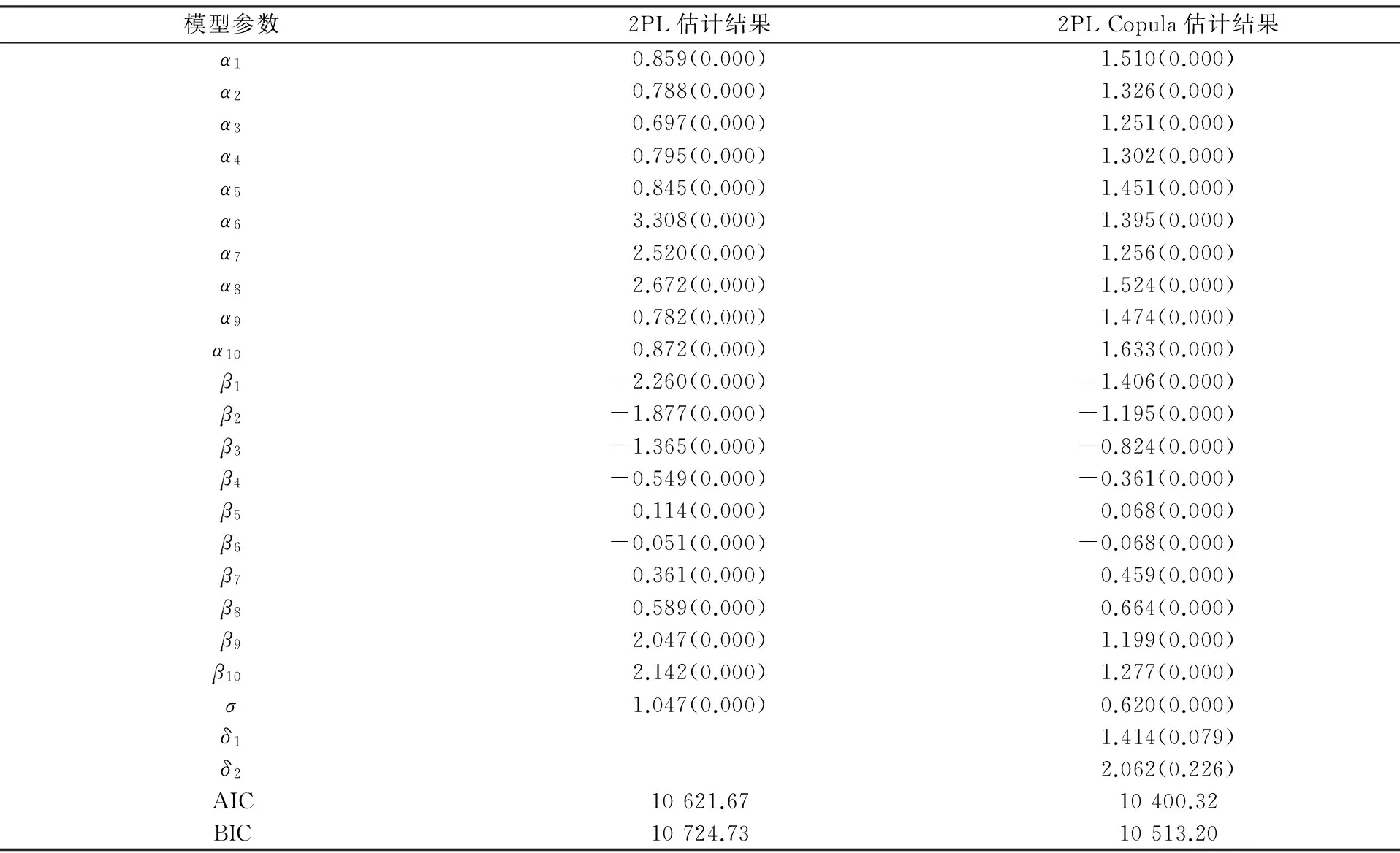
(Ⅳ) ∀a,b∈[0,1]N,∀n=1,2,…,N,an B=[a,b]=[a1,b1]×[a2,b2]×…×[aN,bN], Skalar定理 设F(·,…,·)为具有边缘分布F1(·),F2(·),…,FN(·)的联合分布函数,且存在一个Copula函数C(·,…,·),满足 F(x1,x2,…,xN)=C(F1(x1),F2(x2),…,FN(xN)). 若F1(·),F2(·),…,FN(·)连续,则C唯一确定;若F1(·),F2(·),…,FN(·)为一元分布,C为相应的Copula函数,则F(·,…,·)是具有边缘分布F1(·),F2(·),…,FN(·)的联合分布函数. 本文采用阿基米德Copula分布函数[11-12],其表达式为 C(u1,u2,…,uN)=φ-1(φ(u1)+φ(u2)+…+φ(uN)). 其中:函数φ(·)为阿基米德Copula函数C(·,…,·)的生成元,是一个凸的减函数;φ-1(·)是生成元φ(·)的逆函数,在[0,∞)区间完全单调.下面给出两个比较重要的阿基米德Copula函数. Frank Copula函数: 当N=2时,δ≠0.若δ→-∞,则C→C-;若δ→0,则C→C⊥;若δ→+∞,则C→C+. Cook-Johnson Copula函数: 其中δ>0.若δ→0,则C→C⊥;若δ→+∞,则C→C+. 假定Ypi为被试p对题目i的取值为0或1的二值反应变量,假定被试能力为θp,题目区分度参数和难度参数为αi,βi.定义连续型潜在变量Xpi,且Xpi=αi(θp-βi)+pi,反应变量Ypi和潜变量Xpi满足 Ypi=I(Xpi>0)=I(pi>-αi(θp-βi)). 根据不同的测验背景,假定将{1,2,…,I}分割为S个不交的子集J1,…,JS,其中Js中有Is个题目.类似地误差向量p也分为S块其中pi,i∈Js),不同子集的残差分量是相互独立的,同一子集内部的残差项假定是可交换的. 被试p的反应向量Yp的分布为 具体地,假定I=2,Js=1,2,则反应向量(Yp1,Yp2)取值为(0,0)的概率为 由最后一个等式可见,Copula函数将离散型反应向量(Yp1,Yp2)的联合分布转换为连续型向量(Xp1,Xp2)的分布.(Yp1,Yp2)取其他值的概率为: P(Yp1=1,Yp2=1|θp)=1-FXp1|θp(0|θp)-FXp2|θp(0|θp)+Cs(FXp1|θp(0|θp),FXp2|θp(0|θp)); P(Yp1=1,Yp2=0|θp)=FXp2|θp(0|θp)-Cs(FXp1|θp(0|θp),FXp2|θp(0|θp)); P(Yp1=0,Yp2=1|θp)=FXp1|θp(0|θp)-Cs(FXp1|θp(0|θp),FXp2|θp(0|θp)). 为展示Copula的引入对反应相依模型的拟合效果,给出计算题目1和题目2在给定能力θp下的条件优势比(odds ratio)指标 其中C=C(FXp1|θp(0|θp),FXp2|θp(0|θp)).简单起见,取项目参数α1=α2=1,β1=β2=0,从而对数优势比可以看作关于δ和θ的函数,此时Frank Copula和Cook-Johnson Copula模型的对数优势比见图1.由图1可见,优势比随着δ的增加而增加,即Copula相依参数δ可以度量题目反应的相依性.另外,固定δ时,OR值也依赖于θ的取值:Frank Copula模型反映出的两个题目的相依性比较稳定,从图形上看就是OR值趋于平稳,在δ取极端较大值或较小值时,OR关于θ取值对称;相反,Cook-Johnson Copula模型的OR值随着θ的增加而增加.两种Copula函数体现的相依结构截然不同. (a) Frank Copula模型对数优势比 (b) Cook-Johnson Copula模型对数优势比> 采用边际最大似然法(MML)来估计2PL Copula模型.[7,13]似然函数为 其中φ(θp|σ2)为参数θp的正态分布密度函数(θp~N(0,σ2)).一般将上式取对数,然后采用拟牛顿法求解,其中关于θp的积分需要Gauss-Hermite象限积分法近似. 假定1 000人参加共10个题目的英语阅读理解测验,反应值为0或1.那么针对短文同一部分的几个问题的反应很有可能具有相关性.首先对数据进行探索性分析,运用Mantel-Haenszel(MH)统计量法[14]检验题目之间的相关性.MH计算两题目反应间的优势比是否关于θ是恒定的,MH值越大,题目间的相关性越强.基于MH统计量的相关矩阵见图2,聚类图见图3.易见,题目{4,5}的相关值为8.63,题目{6,7},{6,8},{7,8}之间的相关值分别为10.15,8.40,7.45,再结合聚类图,将{4,5}和{6,7,8}分别归为一类.综上,对反应数据分别采用两种方法建模. 01.48472.41921.369701.809500.451890-0.21871-1.44580-0.2280800.577350001.18361.295700.955480.021093-1.99520-0.821210.306280-0.0455190000.941611.54790-1.125900-1.32040-2.32900-0.4330500.05447200008.62870-2.976300-3.41120-2.58670-0.0229430.18785000000-2.003400-2.98880-3.596901.967000-1.32080000000010.152708.40470-3.787900-3.26310000000007.44790-1.650900-2.70600000000000-0.408510-0.3298600000000002.1693000000000000æèççççççççççöø÷÷÷÷÷÷÷÷÷÷ 图2 题目间基于MH的相关矩阵 图3 题目聚类图 第一种模型,假定局部独立性仍然成立,即 其中条件反应概率为2PL模型 第二种模型,采用Copula函数建模,分别求出J1={4,5}和J2={6,7,8}的联合反应概率,各个题目的边际反应概率仍采用2PL模型.对于J1和J2分别采用Frank Copula和Cook-Johnson Copula,条件似然函数为 表1 2PL模型和2PL Copula模型的参数估计 [1] ALLEN M J,YEN W M.Introduction to measurement theory[M].LongGrove:Waveland Press,2002:25-150. [2] BAKER F B,KIM S H.Item response theory:parameter estimation techniques[M].New York:Marcel Dekker,2004:56-93. [3] IP E H.Adjusting for information inflation due to local dependence in moderately large item clusters[J].Psychometrika,2000,65:73-91. [4] IP E H.Testing for local dependence in dichotomous and polutomous item response models[J].Psychometrika,2001,66:109-132. [5] IP E H.Locally dependent latent trait model and the Dutch identity revisited[J].Psychometrika,2002,67:367-386. [6] HOSKENS M,DE BOECK P.A parametric model for local dependencies among test items[J].Psychological Methods,1997,2(3):261-277. [7] DE BOECK P,WILSON M.Explanatory item response models:a generalized linear and nonlinear approach[M].New York:Springer,2004:36-90. [8] BRADLOW E T,WAINER H,WANG X.A Bayesian random effects model for testlets[J].Psychometrika,1999,64:153-168. [9] VERHELST N D,GLAS C A W.A dynamic generalization of the Rasch model[J].Psychometrika,1993,58:395-415. [10] NELSEN R B.An introduction to Copulas[M].New York:Springer,1999:15-50. [11] JOE H.Parametric families of multivariate distributions with given margins[J].Journal of Multivariate Analysis,1993,46:262-282. [12] JOE H.Multivariate models and dependence concepts[M].London:Chapman & Hall,1997:54-98. [13] 徐俊彦,苗壮,刘庆怀.解多项式双层规划最优解的参数化方法 [J].东北师大学报(自然科学版),2015,47(3):9-11. [14] MANTEL N,HAENSZEL W.Statistical aspects of the analysis of data from retrospective studies of disease[J].Journal of National Cancer Institute,1959,22:719-748. [15] LITTLE R J A,RUBIN D B.Statistical analysis with missing data[M].2nd ed.New York:John Wiley & Sons,2004:22-44. (责任编辑:李亚军) A Copula model for residual dependency in item response model FU Zhi-hui1,2,LIU Luo-man1,MENG Xiang-bin3 (1.School of Mathematics and System Science,Shenyang Normal University,Shenyang 110034,China;2.School of Mathematics and Statistics,Northeast Normal University,Changchun 130024,China;3.Faculty of Education,Northeast Normal University,Changchun 130024,China) In educational and psychological measurement,most item response theory models are not robust to violations of local independence.A new class of models that makes use of Copulas to deal with local item dependencies is introduced.These models belong to the bigger class of marginal models in which marginal and association structure are modeled separately.It is shown how this approach overcomes some of the problems associated with other local item dependency models. item response model;local item dependency;Copula function 1000-1832(2017)02-0041-06 10.16163/j.cnki.22-1123/n.2017.02.009 2015-12-07 国家自然科学基金资助项目(11201313,11571069,11501094,31400897). 付志慧(1979—),女,博士,副教授,主要从事数理统计研究. O 212.1 [学科代码] 110·6735 A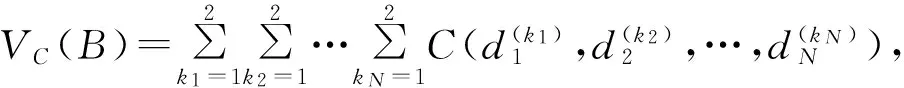
2 相依反应数据的Copula模型
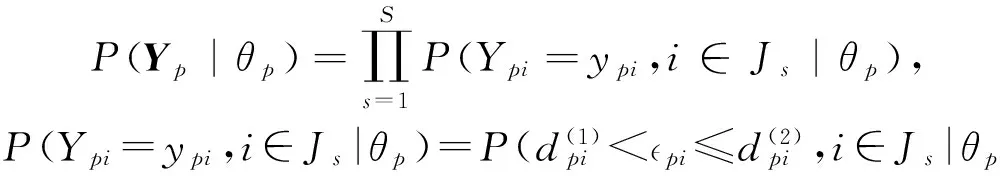
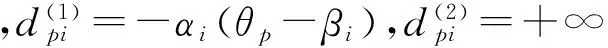
3 算例
4 讨论
