超代数上广义李超导子

袁 鹤

(吉林师范大学数学学院，吉林 四平 136000)

超代数上广义李超导子

袁 鹤

(吉林师范大学数学学院，吉林 四平 136000)

利用超代数上的函数恒等式理论，证明了超代数上的广义李超导子可以表示成一个广义超导子和一个线性映射之和.

函数恒等式；超代数；广义李超导子

0 引言

设R是环，若R上加法映射d满足d(xy)=d(x)y+xd(y)，x，y∈R，则称d是R上的导子.若R上加法映射d满足d[x，y]=[d(x)，y]+[x，d(y)]，x，y∈R，则称d是R上的李导子.显然，每个导子都是李导子，那么反之是否成立呢?Bresar[1]证明了素环上的李导子可以表示成一个导子和一个加法映射之和.文献[2]将这个结果推广到了超代数上，得到超代数上的李超导子可以表示成一个超导子和一个线性映射之和.

随着对导子的研究不断深入，学者们对广义导子的研究也日益增多.1998年，Hvala[3]给出了环上广义导子的定义：若对于环R上的加法映射g，存在R上导子d满足g(xy)=g(x)y+xd(y)，x，y∈R，则称g是R上的广义导子.Hvala[4]还证明了素环上的广义李导子可以表示成一个广义导子和一个中心映射之和.本文将利用超代数上的函数恒等式理论把这个结果推广到超代数上.

函数恒等式理论是一个比较新的理论，人们用它来研究函数的表达式或者满足某函数恒等式的环的结构.这个理论源于交换映射理论[5]，后来逐渐被应用到很多方面.2000年，Beidar和Chebotar[6-7]提出的d-自由集理论为函数恒等式理论的研究提供了强有力的工具，使函数恒等式理论的研究取得了实质性的突破并快速发展.学者们利用d-自由集理论解决了Herstein提出的关于李映射的猜想.[8-10]2009年，王宇[11]确定了素超代数上的函数恒等式理论，并利用此理论研究了素超代数上的李超同态.在上述工作的基础上，王宇[12]又确立了超代数上的函数恒等式理论，给出了d-超自由集和拟超多项式的定义.本文将利用文献[12]中结果研究超代数上的广义李超导子的表示形式.

1 预备知识

下面给出超导子，广义超导子，李超导子和广义李超导子的定义.

设A是超代数且k∈{0，1}，称一个A到A的Φ-线性映射dk是度为k的超导子，如果其满足dk(Ai)⊆Ak+i，i∈Z2，且dk(ab)=dk(a)b+(-1)k|a|adk(b)，a，b∈A0∪A1.如果d=d0+d1，则称d是A上的超导子.

设A是超代数且i∈{0，1}，称一个A到A的Φ-线性映射ɡi是度为i的广义超导子，如果其满足ɡi(Aj)⊆Ai+j，j∈Z2，且存在A上度为i的超导子di使得ɡi(ab)=ɡi(a)b+(-1)i|a|adi(b)，a，b∈A0∪A1.如果g=ɡ0+ɡ1，则称g是A上的广义超导子；d=d0+d1为g的伴随超导子.

设A是超代数且j∈{0，1}，称一个A到A的Φ-线性映射hj是度为j的李超导子，如果其满足hj(Ai)⊆Ai+j，i∈Z2，且hj([a，b]s)=[hj(a)，b]s+(-1)j|a|[a，hj(b)]s，a，b∈A0∪A1.如果h=h0+h1，则称h是A上的李超导子.

设A是超代数且m∈{0，1}，称一个A到A的Φ-线性映射fm是度为m的广义李超导子，如果其满足fm(Aj)⊆Am+j，j∈Z2，且存在A上度为m的李超导子hm使得对于任意的a，b∈A0∪A1有

fm([a，b]s)=fm(a)b-(-1)|a||b|fm(b)a+(-1)m|a|ahm(b)-(-1)m|b|+|a||b|bhm(a).

如果f=f0+f1，则称f是A上的广义李超导子；h=h0+h1为f的伴随李超导子.

下面等式对于研究超代数上广义超导子的表示形式相当重要：

[aibj，ck]s=[ai，bjck]s+(-1)ij+ik[bj，ckai]s，ai，bj，ck∈A0∪A1.

(1)

2 主要结果

本节给出超代数和素超代数上广义李超导子的表示形式.

定理1 设A=A0⨁A1是超代数，Q是含有单位元的超代数且A是Q的子代数，C是Q的中心.若f：A→Q是广义李超导子且A是Q的3-超自由子集，则存在广义超导子ɡ：A→Q和线性映射l：A→C+Cω，满足f(x)=ɡ(x)+l(x)，x∈A.

5)标准化因子norm。lucene的打分公式中，标准化因子由3个参数决定：document boost表示文档的重要性；Field boost表示域重要性；lengthNorm(field)表示域中包含的Term总数。

证明 由广义李超导子的定义，设fm是度为m的广义李超导子，hm是度为m的李超导子，m∈{0，1}.应用fm于(1)式有

0=fm(aibj)ck-(-1)ik+jkfm(ck)aibj+(-1)m(i+j)aibjhm(ck)-
(-1)mk+ik+jkckhm(aibj)-fm(ai)bjck+(-1)ij+ikfm(bjck)ai-
(-1)miaihm(bjck)+(-1)m(j+k)+ij+ikbjckhm(ai)-(-1)ij+ik(fm(bj)ckai-
(-1)jk+ijfm(ckai)bj+(-1)mjbjhm(ckai)-(-1)m(i+k)+jk+ijckaihm(bj))，

其中ai，bj，ck∈A0∪A1.由文献[2]，hm=dm+pm，其中dm是度为m的超导子，pm：A→C+Cω是线性映射.因此

0=fm(aibj)ck-fm(ai)bjck-(-1)miai(dm(bj)ck+(-1)mjbjdm(ck)+pm(bjck))+
(-1)ij+ik(fm(bjck)ai-fm(bj)ckai-(-1)mjbj(dm(ck)ai+(-1)mkckdm(ai)+
pm(ckai)))+(-1)ik+jk(fm(ckai)bj-fm(ck)aibj-(-1)mkck(dm(ai)bj+
(-1)miaidm(bj)+pm(aibj)))+(-1)m(i+j)aibj(dm(ck)+pm(ck))+
(-1)m(j+k)+ij+ikbjck(dm(ai)+pm(ai))+(-1)m(i+k)+ik+jkckak(dm(bj)+pm(bj)).

(2)

定义映射B：A×A→Q，

B(x，y)=fm(xy)-fm(x)y-(-1)m|x|xdm(y)，x，y∈A0∪A1.

由(2)式有

0=B(ai，bj)ck+(-1)ij+ikB(bj，ck)ai+(-1)ik+jkB(ck，ai)bj-
(-1)miaipm(bjck)-(-1)mj+ij+ikbjpm(ckai)-(-1)mk+ik+jkckpm(aibj)+
(-1)m(i+j)aibjpm(ck)+(-1)m(j+k)+ij+ikbjckpm(ai)+(-1)m(i+k)+ik+jkckaipm(bj)，

其中ai，bj，ck∈A0∪A1.因为A是Q的3-超自由子集，由文献[12]有：

(3)

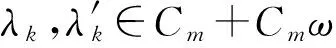
fm(xyz)=B(xy，z)+fm(xy)z+(-1)m(|x|+|y|)xydm(z)=
B(xy，z)+(B(x，y)+fm(x)y+(-1)m|x|xdm(y))z+(-1)m(|x|+|y|)xydm(z)；

fm(xyz)=B(x，yz)+fm(x)yz+(-1)m|x|xdm(yz)=
B(x，yz)+fm(x)yz+(-1)m|x|x(dm(y)z+(-1)m|y|ydm(z)).

两式相减得

B(xy，z)+B(x，y)z-B(x，yz)=0，

(4)

其中x，y，z∈A0∪A1.

将(3)式代入(4)式中，整理得：

由文献[12]中定理3.7有：

μ3(x1)=μ4(x1)，μ4(x1y0)=-v3(x1，y0)；

μ1(x1y1)=-v4(x1，y1).

由B的定义，

B(x0，y1)=fm(x0y1)-fm(x0)y1-x0dm(y1)，

B(y1，x0)=fm(y1x0)-fm(y1)x0-(-1)my1dm(x0).

上面两式相减得

B(x0，y1)-B(y1，x0)=fm([x0，y1]s)-(fm(x0)y1-fm(y1)x0)-
(x0dm(y1)-(-1)my1dm(x0))=x0pm(y1)-(-1)my1pm(x0)，

从而

λ2x0y1+μ2(x0)y1+v2(x0，y1)-μ3(y1)x0-v3(y1，x0)-x0pm(y1)+(-1)my1pm(x0)=0.

由文献[12]中定理3.7有λ2=0，λ4=0.因此

B(x0，y0)=μ1(x0)y0-μ1(x0y0)，
B(x0，y1)=μ1(x0)y1-μ4(x0y1)，
B(x1，y0)=μ4(x1)y0-μ4(x1y0)，
B(x1，y1)=μ4(x1)y1-μ1(x1y1).

(5)

设

由(5)式，fm(xy)+μm(xy)=fm(x)y+(-1)m|x|xdm(y)+μm(x)y，x，y∈A0∪A1.

设fm+μm=ɡm，l=-μ0-μ1，则ɡ=ɡ0+ɡ1是广义超导子，l：A→C+Cω是线性映射.结论证毕.

由文献[12]中定理4.16和定理1可得下面结论.

推论1 设A=A0⨁A1是素超代数，Q是A的极大右商环，C是A的扩展型心.若f：A→Q是广义李超导子且deg(A1)≥7，则存在广义超导子ɡ：A→Q和线性映射l：A→C+Cω，满足f(x)=ɡ(x)+l(x)，x∈A.

[1] BREASAR M.Commuting traces of biadditive mappings：commutativity-preserving mappings and Lie mappings[J].Trans Amer Math Soc，1993，335(2)：525-546.

[2] 袁鹤.超代数上的超导子和三角代数上的广义导子[D].长春：吉林大学，2014.

[3] HVALA B.Generalized derivations in rings[J].Comm Algebra，1998，26(4)：1147-1166.

[4] HVALA B.Generalized Lie derivations in prime rings[J].Taiwanese J Math，2007，11(5)：1425-1430.

[5] BREASAR M.Centralizing mappings and derivations in prime rings[J].J Algebra，1993，156：385-394.

[6] BEIDAR K I，CHEBOTAR M A.On functional identities andd-free subsets of rings：Ⅰ[J].Comm Algebra，2000，28(8)：3925-3951.

[7] BEIDAR K I，CHEBOTAR M A.On functional identities andd-free subsets of rings：Ⅱ[J].Comm Algebra，2000，28(8)：3953-3972.

[8] BEIDAR K I，BREASAR M，CHEBOTAR M A，et al.On Herstein’s Lie map conjectures：Ⅰ[J].Trans Amer Math Soc，2001，353(10)：4235-4260.

[9] BEIDAR K I，BREASAR M，CHEBOTAR M A，et al.On Herstein’s Lie map conjectures：Ⅱ[J].J Algebra，2001，238：229-264.

[10] BEIDAR K I，BREASAR M，CHEBOTAR M A，et al.On Herstein’s Lie map conjectures：Ⅲ[J].J Algebra，2002，249：59-94.

[11] WANG Y.Functional identities and Lie superhomomorphisms on prime superalgebras[J].Comm Algebra，2009，37(12)：4193-4226.

[12] WANG Y.Functional identities in superalgebras[J].J Algebra，2013，382：144-176.

(责任编辑：李亚军)

Generalized Lie superderivations of superalgebras

YUAN He

(College of Mathematics，Jilin Normal University，Siping 136000，China)

It is proved that a generalized Lie superderivation is the sum of a generalized superderivation and a linear mapping by using the theory of functional identities in superalgebras.

functional identity；superalgebra；generalized Lie superderivation

1000-1832(2017)02-0011-04

10.16163/j.cnki.22-1123/n.2017.02.003

2015-11-18

国家自然科学基金资助项目(11471090)；吉林省科技发展计划资助项目(20170520068JH)；吉林省教育厅“十三五”科学技术研究项目(吉教科合字[2016]第214号).

袁鹤(1983─)，女，博士，讲师，主要从事环理论研究.

O 152 [学科代码] 110·21

A