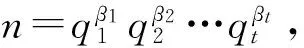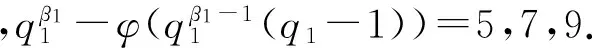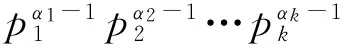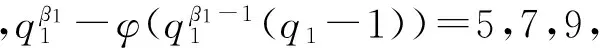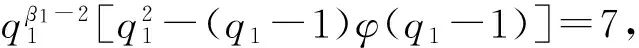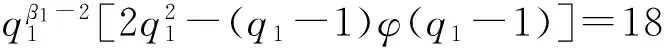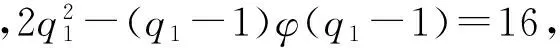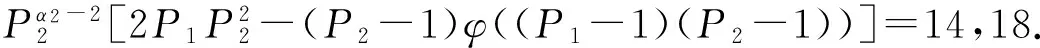一个带有复合Euler函数方程的正整数解

王 洋，张四保

(1.四川交通职业技术学院公共教学部，四川 成都 611130；2.喀什大学数学与统计学院，新疆 喀什 844008)

一个带有复合Euler函数方程的正整数解

王 洋1，张四保2

(1.四川交通职业技术学院公共教学部，四川 成都 611130；2.喀什大学数学与统计学院，新疆 喀什 844008)

设φ(n)为Euler函数，探讨了带有复合欧拉函数的方程φ(φ(n-φ(φ(n))))=2正整数解的问题，利用初等方法给出了其所有的正整数解.

Euler函数；正整数解；初等方法

1 预备知识

设n为正整数，φ(n)为Euler函数[1]，φ(n)在正整数n上的值为不超过n且与n互素的正整数个数.Euler函数φ(n)是数论中的一个重要函数，它与著名的Smarandache函数有着莫大的关系，众多学者对与之相关的方程进行了大量研究.[2-7]

对于带有复合欧拉函数方程正整数解的研究可参见文献[8-11].本文讨论带有复合欧拉函数的方程

φ(φ(n-φ(φ(n))))=2

(1)

的正整数解问题，并通过初等方法给出其所有的正整数解.

引理1[12]方程φ(x)=2P的正整数解x为：当P=1时，x=3，4，6；当P=2时，x=5，8，10，12；当P=3时，x=7，9，14，18.

引理2[13]若n为大于等于2的整数，则φ(n)

2 主要结论及证明

定理1 方程(1)的所有正整数解为n=6，7，9，10，11，12，13，14，16，17，22.

证明 由引理1可知φ(x)=2的所有正整数解为x=3，4，6，从而方程(1)为φ(n-φ(φ(n)))=3，4，6.再由引理2可知，φ(n-φ(φ(n)))=4，6.

由引理1可知：当φ(n-φ(φ(n)))=4时，n-φ(φ(n))=5，8，10，12；当φ(n-φ(φ(n)))=6时，n-φ(φ(n))=7，9，14，18.由此可将n-φ(φ(n))的值分为n-φ(φ(n))=5，7，9与n-φ(φ(n))=8，10，12，14，18这两种情形.

情形1n-φ(φ(n))=5，7，9.

即

情形1.1β1≠0，βi=0，i=2，3，…，t.

情形1.1.1β1=1.

当αj=0(j=1，2，…，k)时，q1-1=2γ，从而 2γ-φ(2γ)=4，6，8.因而2γ-1=4，6，8，γ=3，4.此时，n=9，17是方程(1)的二个正整数解.

当αj(j=1，2，…，k)中至少有1个满足αj≠0时，有

(2)

此时，α1=1，αj=0，j=2，3，…，k；p1=3；q1-1=6.从而n=7是方程(1)的正整数解.

有

由于2p1p2…pk-(p1-1)(p2-1)…(pk-1)>(p1-1)(p2-1)…(pk-1)≥2，因而方程(1)无正整数解.

情形1.1.2β1≥2.

情形1.2β1≠0，β2≠0，βi=0，i=3，4，…，t.

情形1.2.1β1=1，β2=1.

此时，q1q2-φ((q1-1)(q2-1))=5，7，9.注意到

q1q2-φ((q1-1)(q2-1))=(q1-1)(q2-1)-φ((q1-1)(q2-1))+q1+q2-1>8，

因而只讨论q1q2-φ((q1-1)(q2-1))=9的情形.

事实上，当q1=3，q2=5时，q1q2-φ((q1-1)(q2-1))=9不成立；当q1=3，q2>5时，

q1q2-φ((q1-1)(q2-1))=(q1-1)(q2-1)-φ((q1-1)(q2-1))+q1+q2-1>9；

当q1≥5，q2≥7时，

q1q2-φ((q1-1)(q2-1))=(q1-1)(q2-1)-φ((q1-1)(q2-1))+q1+q2-1>9.

故此时方程(1)无正整数解.

情形1.2.2β1，β2中至少有一个大于等于2.

类似于情形1.2.1的讨论可知此时方程(1)无正整数解.

情形1.3βi中有三个或者三个以上不等于0.

类似于情形1.2.1的讨论可知此时方程(1)无正整数解.

情形2n-φ(φ(n))=8，10，12，14，18.

当βi=0(i=1，2，…，t)时，2δ-φ(2δ-1)=8，10，12，14，18.显然此时δ≥4，进而有2δ-2×3=8，10，12，14，18.此时只有2δ-2×3=12有正整数解δ=4，故n=24=16是方程(1)的正整数解.同时可知当δ≥5时，方程(1)无正整数解.因而，在讨论至少存在某个βi≠0时δ的情形时，只需考虑1≤δ≤4.

情形2.1δ=1.

此时，

(3)

情形2.1.1β1≠0，βi=0，i=2，3，…，t.

此时，由(3)式有

(4)

当β1=1时，由(4)式可知 2q1-φ(q1-1)=8，10，12，14，18.当q1=5时，2q1-φ(q1-1)=8，即n=2×5=10是方程(1)的正整数解；当q1=7时，2q1-φ(q1-1)=12，即n=2×7=14是方程(1)的正整数解；当q1=11时，2q1-φ(q1-1)=18，即n=2×11=22是方程(1)的正整数解；当q1=13时，2q1-φ(q1-1)=8，10，12，14，18均不成立；当q1≥17时，2q1-φ(q1-1)=(q1-1)-φ(q1-1)+(q1+1)>18，因而此时方程(1)无正整数解.

情形2.1.2β1≠0，β2≠0，βi=0，i=3，4，…，t.

此时，

(5)

当β1=1，β2=1时，由(5)式有 2q1q2-φ((q1-1)(q2-1))=8，10，12，14，18.由于

2q1q2-φ((q1-1)(q2-1))=2(q1-1)(q2-1)-φ((q1-1)(q2-1))+2q1+2q2-2=

(q1-1)(q2-1)-φ((q1-1)(q2-1))+2q1+2q2-2+(q1-1)(q2-1)>18，

因而此时方程(1)无正整数解.并由该情形的讨论可知，当βi(i=1，2，…，t)中有多于两个不等于0时，方程(1)亦无正整数解.

故此时方程(1)无正整数解.并由该情形的讨论可知，当β1，β2中至少有一个大于等于2时，方程(1)亦无正整数解.

仿照t=1情形的讨论可得：当t=2时，n=22×3=12是方程(1)的正整数解；当t=3与t=4时，方程(1)无正整数解.

综合以上讨论，即得定理1结论.

[1] 闵嗣鹤，严仕健.初等数论[M].第三版.北京：高等教育出版社，2003：58.

[2] 孙翠芳，程智.若干包含Euler函数φ(n)的方程[J].吉林大学学报(理学版)，2012，50(5)：859-862.

[3] 张四保，刘启宽.关于Euler函数一个方程的正整数解[J].东北师大学报(自然科学版)，2015，47(3)：49-54.

[4] 史宝怀，潘晓玮.关于数论函数方程φ(x1…xn-1xn)=m(φ(x1)+…+φ(xn-1)+φ(xn))[J].数学的实践与认识，2014，44(24)：307-310.

[5] 张文鹏.关于F.Smarandache函数的两个问题[J].西北大学学报(自然科学版)，2008，38(2)：173-176.

[6] 范盼红.关于F.Smarandache函数和欧拉函数的三个方程[J].黑龙江大学学报(自然科学版)，2012，29(5)：626-628.

[7] 呼家源，秦伟.一个包含Smarandache Ceil函数的对偶函数及Euler函数的方程及其可解性[J].西北大学学报(自然科学版)，2013，43(3)：364-366.

[8] ZHANG T P.An equation involving Euler functionφ(n)[J].Scientia Magna，2008，4(1)：109-112.

[9] 田呈亮，付静，白维祖.一个包含欧拉函数的方程[J].纯粹数学与应用数学，2010，26(1)：96-98.

[10] 多布杰.关于欧拉函数方程φ(φ(x)) = 2t的可解性[J].纯粹数学与应用数学，2014，30(6)：564-568.

[11] 吕志宏.一个包含Euler函数的方程[J].西北大学学报(自然科学版)，2006，36(1)：17-20.

[12] 姜友谊.关于Euler 函数方程φ(x)=m的解[J].重庆工业管理学院学报，1998，12(5)：91-94.

[13] ROSEN K H.Elementary number theory and its applications[M].5th ed.London：Addison Wesley，2005：225.

(责任编辑：李亚军)

Positive integer solutions of an equation involving compound Euler function

WANG Yang1，ZHANG Si-bao2

(1.Department of Public Teaching，Sichuan Vocational and Technical College of Communications，Chengdu 611130，China；2.School of Mathematics and Statistics，Kashgar University，Kashgar 844008，China)

Letφ(n) be Euler function.The problem of positive integer solutions of an equation involving compound Euler functionφ(φ(n-φ(φ(n))))=2 is studied.All the positive integer solutions of it are given by using elementary method.

Euler function；positive integer solutions；elementary method

1000-1832(2017)02-0021-04

10.16163/j.cnki.22-1123/n.2017.02.005

2015-09-27

新疆维吾尔自治区自然科学基金资助项目(2016D01A014).

王洋(1985—)，男，博士，讲师，主要从事高等数学教学及应用数学研究；通信作者：张四保(1978—)，男，硕士，副教授，主要从事数论研究.

O 156 [学科代码] 110·17

A