一种削弱双转子永磁电机齿槽转矩方法

高起兴，井立兵

(三峡大学，宜昌443002)

0 引 言

双转子永磁电机具有结构小巧、噪声小、效率高的优点，可以较大幅度减小电机的重量和体积，提高电机的输出转矩和运行效率［1－2］。但齿槽转矩是永磁电机的固有特性，由永磁体磁场与齿槽互相作用产生，齿槽转矩的出现会造成电机的振动和噪声，影响电机运行质量［3－5］。

双转子电机结构的特殊之处在于:电机由内转子、中间定子、外转子组成，电机的内、外转子共同驱动一根转轴，总齿槽转矩为内、外齿槽转矩之和;并且由于内、外电机半径尺寸相距较大，所以外侧齿槽转矩幅值远大于内侧［6］。为了有效削弱双转子电机齿槽转矩，中、外学者做了很多研究。文献［7］研究用斜极的方法分别减小内、外齿槽转矩;文献［8－10］提出可以利用双转子电机的特殊结构，通过内、外齿槽转矩产生相位差使二者相互抵消，不过没有给出相位移动角度的公式。文献［10］比较了上述两种方法，得出内、外转子齿槽转矩相互抵消的方法有更好降低转矩波动的效果，但仍存在的问题是内、外转子的齿槽转矩幅值相距较大，前者不足以引起后者幅值波形较大的变化。

为了更有效的削弱齿槽转矩，本文针对双转子极、槽数量组合，设计了一种磁极对称偏移方法，可降低外侧齿槽转矩幅值且不改变外齿槽转矩的周期大小和初始相位，通过寻优找到合适磁极偏移角度使内、外齿槽转矩幅值大致相等;再通过改变内、外槽的相对位置使内、外转子齿槽转矩存在一定相位差，以此来削弱电机合齿槽转矩，并用有限元验证了此方法。

1 电机齿槽转矩计算

对于双转子永磁电机，内、外转子上的永磁体均与中间定子槽相互作用产生齿槽转矩，总的齿槽转矩为内、外齿槽转矩之和。为了便于研究，本文做以下假设:

永磁电机的齿槽转矩可表示［11］:

1)电枢铁心的导磁率无穷大，即μFe=∞;

2)θ=0的位置可设定在任意一个磁极的中心线上;

3)内(或外)电机永磁体的形状、尺寸、性能皆相同。

因此，双转子电机外磁场能量可以看作是外气隙和外永磁体内的能量:

对于任意角α，外气隙的径向磁密可以表示:

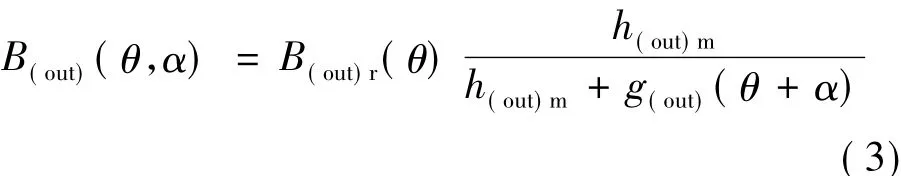
式中:B(out)r(θ)为外侧永磁体的剩磁向圆周侧的分布;h(out)m为外侧永磁体充磁的长度;g(out)(θ，α)为中间定子外侧齿中心线与外转子磁极中心线夹角为α时的有效气隙长度向圆周侧的分布。所以，式(2)可以表示:

所以，对θ) 和{h(out)m/［h(out)m+g(out)(θ，α)］}2进行傅里叶分解得到磁场能量进而可算出齿槽转矩。θ)和 {h(out)m/［h(out)m+g(out)(θ，α)］}2的傅里叶展开式:

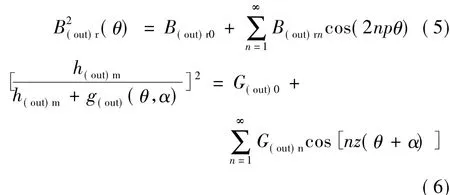
式中:n为使nz/(2p)能为整数的最小整数;R1和R2分别为中间定子外径和外转子内径;LFe为电枢铁心的长度。

同理，设内转子齿槽转矩为T(in)cog，其表达式:

式中:z和p分别为“外电机”的齿槽数和极对数。综合式(1)、式(4)、式(5)、式(6)，外齿槽转矩的表达式可得:

式中:R3和R4分别为内转子外径和中间定子内径。

内、外双转子永磁电机合成的总齿槽转矩:

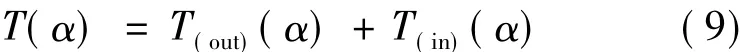
2 优化计算与仿真

本文选取6极36槽双转子永磁电机为例，表1为电机主要参数。

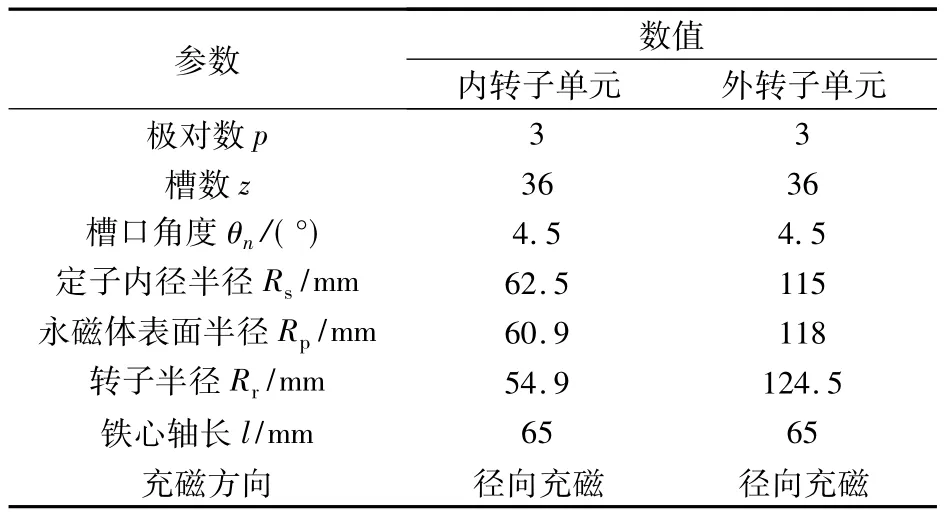
表1 电机模型参数

图1为双转子永磁电机的二维剖面图。磁钢选用钕铁硼永磁材料，内、外转子转速均设置为1 000 r/min。内转子与中间定子组成“内电机”，外转子与中间定子组成“外电机”，双转子电机由内、外电机复合而成，因此能够达到减小体积、降低重量、加大输出转矩的效果。图2为电机的内、外齿槽转矩以及它们的合成齿槽转矩。

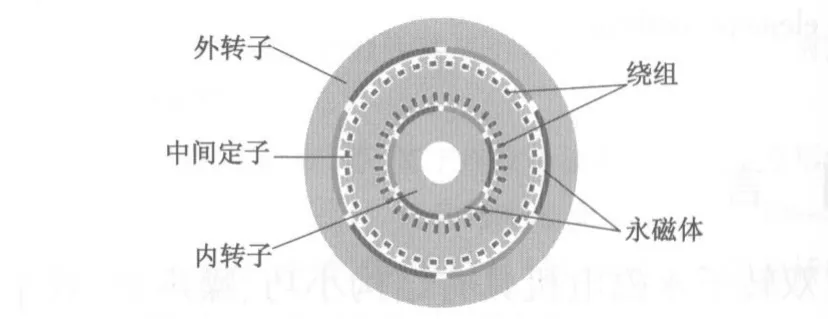
图1 双转子永磁电机二维剖面图

图2 优化前齿槽转矩合成图

2． 1外磁极偏移

由图2可看出，内、外齿槽转矩幅值相距较大，不利于移动相位后的相互消去。文献［12－14］分别证明了各自磁极偏移方式均能有效削弱齿槽转矩，但都没有考虑其对齿槽转矩初始相位和周期大小的改变，因为它对常规单转子电机运行不会造成影响，但对于双转子电机中内、外转子相对相位关系却至关重要［7－9］。

电机的极、槽数量组合与磁极偏移方式是影响磁极变动后齿槽转矩周期和相位的两个因素［15－16］。为了单独削弱外转子齿槽转矩且同时不改变其周期大小及相位初值，本文针对双转子电机常用极、槽组合6极36槽双转子永磁电机(8极48槽亦可同理推导)，设计一种磁极对称偏移的方法。

常规永磁电机齿槽转矩可表示如下［17］:

式中:TNi为傅里叶系数;Nc为槽数z与极数2p的最小公倍数;θ为磁极与定子齿的相对位置角。

将双转子电机中的“内电机”保持不变，“外电机”中的6个磁极中以轴对称的2个磁极分为1组，如图3所示。磁极1－4，2－5，3－6共为3组，让磁极2－5，3－6相对于电机横轴上的磁极1－4，如图3中作对称偏移，齿槽转矩可通过下式合成。

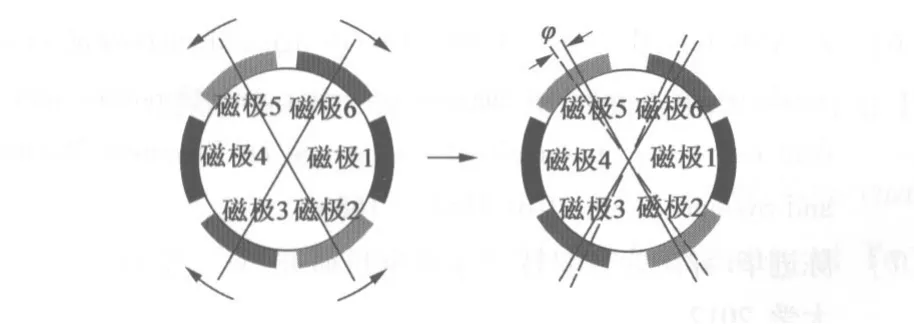
图3 外磁极偏移示意图

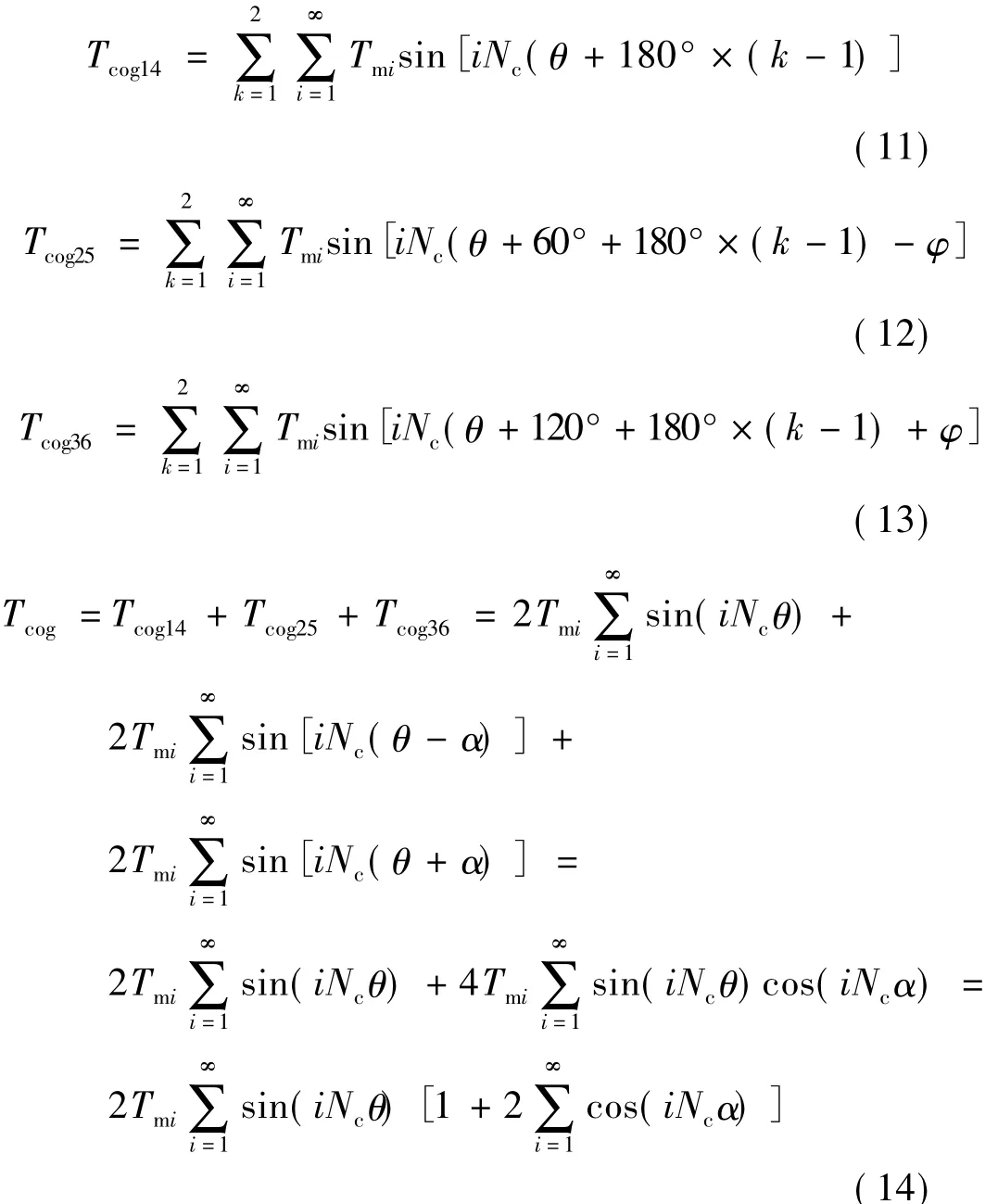
式中:Tcog14为磁极1－4产生的齿槽转矩;Tcog25为磁极2－5产生的齿槽转矩;Tcog36为磁极3－6产生的齿槽转矩;Tmi为单个磁极的傅里叶系数。

从式(14)可以看出，利用本文的对称磁极偏移法，不会改变“外电机”齿槽转矩原始的周期和初始相位。周期不变，利于错相位消去;初始相位不变利于下文槽口角度的计算。

为使Tcog最小，取i=1削去对电机影响最大的齿槽转矩基波影响，根据式(12)，令1+2cos(iNcα)=0，得出当 α =120/(iNc)=3．33 时(Nc=36)，Tcog得最小值。但本文对外磁极的偏移中，不取Tcog的最小值，而取与内齿槽转矩T(in)cog最接近的值T(out)cog。借助有限元计算可以看出，T(out)max＞T(in)cog＞T(out)min，因此可在α=0～33．3°之间寻找到最优值。取 φ 分别为 0，1°，2°，2．5°，2．7°，2．8°，2．9°，3．1°，3．3°，3．5°，3．6°，3．8°和 4°做有限元仿真，如图 4 所示，随着磁极的偏移，在φ=3．3°时，外齿槽转矩幅值最小;φ =2．9°时，外齿槽转矩幅值 T(out)cog=2．4 N·m与内齿槽转矩的幅值T(in)cog=2．3 N·m最接近，因此选择φ=2．9°为本文磁极偏移角度值。

图4 外齿槽转矩幅值随磁极偏移角度移动的变化曲线

图5 、图6分别为外齿槽转矩磁极偏移前后的波形、谐波傅里叶分解对比图。从图中可以看出，磁极偏移后的外齿槽转矩幅值从10 N·m下降到2．4 N·m，一次谐波、二次谐波均有明显下降，并且初始相位、周期大小保持不变，符合预想结果。

图5 齿槽转矩波形

图6 外齿槽转矩傅里叶分解对比图

2． 2 外槽偏移

基于双转子电机的特殊结构，我们不但应该研究齿槽转矩波形的幅值，还应该注意它的相位。一般来说，双转子永磁电机的内、外槽口为径向对齐，内、外齿槽转矩相位一致。总的齿槽转矩为二者的代数和，大于内、外任一个单转子的齿槽转矩。如果把其中一侧槽口整体沿转轴旋转一定角度，内、外齿槽转矩将产生相位差，当两者相位正好相反时，合齿槽转矩最小。

由于槽口移动前，外转子齿槽转矩的周期和相位与内转子完全一致，为使内、外齿槽转矩相位相反，则令外齿槽转矩相位移动半个周期即可。计算出槽偏移角度θ如下:

对于本文6极36槽结构的双转子电机，根据式(15)，θ=5°可获得最小合齿槽转矩，并用有限元验证上述结论。由图7可看出，随着槽口的移动，合齿槽转矩先上升，再下降，当θ=5°时，合齿槽转矩幅值最小为0．33 N·m，从而看出有限元法仿真结果与计算结果完全一致。因此本文取θ=5°为外槽口旋转的角度。而合齿槽转矩先上升的原因是，外齿槽转矩并非理想正弦波，内、外转矩波形走势有所偏差，所以在槽口移动初期，合齿槽转矩会有上升走势。

图8为优化后齿槽转矩的合成图。与图2对比可以看出，优化后的电机内、外齿槽转矩幅值大致相等，相位相反，合成的总齿槽转矩从原始的12．15 N·m优化到 0．33 N·m，降低了97．28%。

3 结 语

针对双转子永磁电机特殊结构，本文研究了一种磁极偏移和槽偏移配合方法来削弱电机的齿槽转矩。设计一种外磁极对称偏移方法，用于降低外齿槽转矩幅值，且保持其周期和初始相位不变;通过计算外槽口移动角度使得内、外齿槽转矩反相位消去。有限元计算得出该优化方法将电机合齿槽转矩降低了97．28%，证明该方法有效、可行。

［1］ CHEN Y Y，QUAN L，ZHU X Y，et al．Electromagnetic Performance Analysis of Double－Rotor Stator Permanent Magnet Motor for Hybrid Electric Vehicle［J］．IEEE Transactions on Magnetics，2012，48(11):4204 －4207．

［2］ LIL B，ZHAOQ Y，SHIG K，et al．Analysis of feasibility of Double－Rotor Motor applied to Hybrid Electric Vehicle［C］//Vehicle Power and Propulsion Conference．IEEE，2008:1 －5．

［3］ 刘婷．表贴式永磁同步电机齿槽转矩削弱方法研究［D］．长沙:湖南大学，2012．

［4］ 肖庆优，黄开胜，陈文敏，等．一种确定永磁同步电动机最佳磁极偏移角度的方法［J］．微特电机，2015，43(12):14 －16．

［5］ 赖文海，黄开胜，洪林，等．基于重复单元内置式单相永磁同步电动机的磁极偏移［J］．微电机，2015，50(8):1 －4．

［6］ ZHANG F G，GAOY G，CHENJH．Design and analysis of a novel wind－power permanent magnet generator with Opposite－rotation dual rotors［C］ International Conference on Electrical Machines and Systems．IEEE，2010:1681 － 1686．

［7］ 陈进华．异向旋转双转子永磁电机研究［D］．沈阳:沈阳工业大学，2012．

［8］ 王法庆．双转子永磁风力发电机研究［D］．济南:山东大学，2007．

［9］ 高钰阁．对转双转子永磁同步风力发电机的设计与分析［D］．沈阳:沈阳工业大学，2010．

［10］ 崔康，杨庆东．内外双转子异构力矩电机齿槽转矩分析［J］．机械工程与自动化，2016(4):33－35．

［11］ 宋伟，王秀和，杨玉波．削弱永磁电机齿槽转矩的一种新方法［J］．电机与控制学报，2004，8(3):214 －217．

［12］ WANGA M，MA DJ，SHUSW．Influenceof magnet poleshifting on cogging torque for PMSG application［C］//International Conference on Electrical Machines and Systems．IEEE，2015:495 －499．

［13］ WANG D H，WANG X H，YANG Y B．Optimization of Magnetic Pole Shifting to Reduce Cogging Torque in Solid－Rotor Permanent－ Magnet Synchronous Motors［J］．IEEE Transactions on Magnetics，2010，46(5):1228 －1234．

［14］ 杨玉波，王秀和，张鑫，等．磁极偏移削弱永磁电机齿槽转矩方法［J］．电工技术学报，2006，21(10):22 －25．

［15］ 刘婷．表贴式永磁同步电机齿槽转矩削弱方法研究［D］．长沙:湖南大学，2012．

［16］ 郭仁，黄守道，高剑．一种基于磁极偏移的永磁电机齿槽转矩最优削弱方法［J］．微特电机，2010，38(10):31 －33．

［17］ ZHU Z Q，HOWE D．Influence of design parameters on cogging torque in permanent magnet machines［J］．IEEE Transactions on Energy Conversion，2001，15(4):407－412．