不同磁致伸缩方程下永磁电机的应力、应变研究

刘现伟，耿跃华

(河北工业大学，天津300130)

0 引 言

由于电机的振动噪声不仅会影响环境质量而且还会使电机的使用寿命折损，因此电机中的振动噪声一直是研究的热点问题［1］。电机中的定子硅钢片是一种磁导率很大的磁性材料，因此，当其处于变化的磁场下会出现沿磁场方向上的应力和由此引起的形变，由于上述情况的出现，就会导致电机定子出现整体的振动并产生噪声。

电机振动噪声的来源一般分为机械噪声、空气动力噪声和电磁噪声等［2］。以往认为电磁噪声中的电磁力是其噪声的主要来源，而随着近些年的研究发现磁致伸缩效应对于电机的振动噪声的影响也有着很大的比重。现阶段磁致伸缩效应的应用大多都是磁致伸缩制动器、传感器的方面，而关于磁致伸缩对电机噪声影响研究还不太成熟［3］。2009 年，Sakda Somkun，Anthony J．Moses对磁致伸缩的各向异性和非取向电工钢的机械特性进行了研究。通过测量研究发现磁致伸缩的各向异性对感应电机定子齿的非对称形变有很大的影响［4］。韩雪岩等人也研究了理想电流和实验电流供电下由电磁力和磁致伸缩效应单独和共同作用下的电机振动［5］，实验条件下得到的定子磁致伸缩位移大约为3．96×10－7m。2015年，沈阳工业大学的张艳丽，李强等人研究了谐波磁场下硅钢片的磁致伸缩特性，得出了结论是谐波磁场下单片硅钢片磁致伸缩引起的噪声明显增大［6］。因此研究磁致伸缩效应对电机振动噪声的影响是有着重要的意义。

为了能准确地研究磁致伸缩效应对电机振动噪声的影响，需要选取合适的方程来进行预测和分析。而应用不同的磁致伸缩本构方程对电机振动噪声的预测分析结果也可能会有所不同。因此本文以单相永磁同步电机为例，研究了几种本构方程对电机振动仿真结果的异同，对于永磁电机主要研究的是磁致伸缩效应对其定子硅钢片的影响。

1 永磁电机的建模与分析

1． 1永磁电机模型

由于所研究的永磁同步电机的模型是轴对称的，并且是可以旋转拉伸的。因此在有限元软件中可以对永磁同步电机由三维模型简化为二维模型，从而可以减少计算量，节约计算时间。利用有限元软件建立的二维永磁同步电机模型和研究中所使用的永磁同步电机相关的参数和参考点如图1和表1所示。

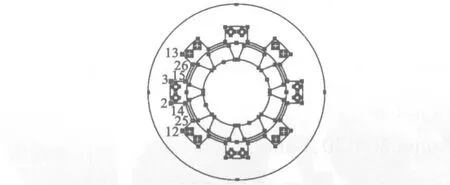
图1 永磁电机模型及参考点

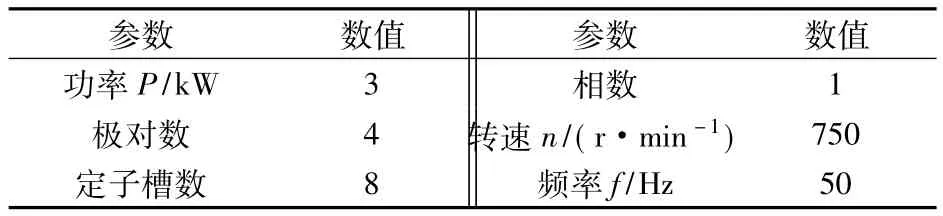
表1 电机主要参数

1． 2模型分析方法

模型分析采用有限元软件COMSOL来实现的，通过软件中的旋转机械－磁与结构力学模块进行耦合，实现电机中的磁－力耦合，得到由磁致伸缩效应引起的电机定子硅钢片的应力与形变的结果。

磁－力耦合分析可以通过两种形式来实现，一种是强耦合形式，通过直接对旋转机械－磁和结构力学模块相应的边界条件和域的设置来直接耦合求解，得到相应的磁通密度、应力、形变等结果，一种是弱耦合形式，即先通过对旋转机械－磁模块的求解得到磁场的结果，再通过找到旋转机械－磁与结构力学模块之间的耦合关系来求解应力与应变。本文采用强耦合的形式来研究不同的磁致伸缩本构方程对永磁电机的振动噪声的影响。

1． 3磁致伸缩本构方程

通过COMSOL软件可以对二维电机模型进行有限元分析求解。应用软件中的旋转机械－磁与结构力学模块对其进行强耦合求解。通过A－φ的方法(A是磁矢势，φ是标量电位)求解电机内部的磁场分布及大小。然后由磁－力耦合得到由磁致伸缩效应引起的应力与形变。磁－力耦合是通过相应的磁致伸缩本构方程来实现的。

对电机硅钢片有限元分析所使用的第一种磁致伸缩本构关系是基于线性压磁方程描述的。方程是由应变和磁通密度方程组成。应变方程包括由应力和外加磁场共同作用时引起的应变。磁通密度方程是由应力和外加磁场产生的磁通密度［7］。当只考虑单一方向上的磁致伸缩时方程可表示:

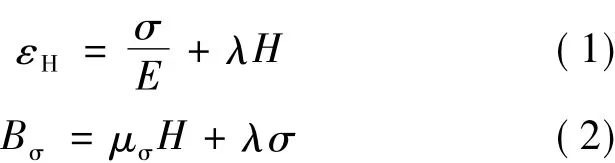
式中:εH为硅钢片在磁场强度为H时的总应变;E为杨氏模量;σ为应力;λ为磁致伸缩系数;H为磁场强度;Bσ为应力作用下的磁感应强度;μσ为应力作用下的磁导率。

对于二维弹性材料而言，应力与应变之间的关系式为σ=Dε，其中D为刚度矩阵，刚度矩阵表达式:

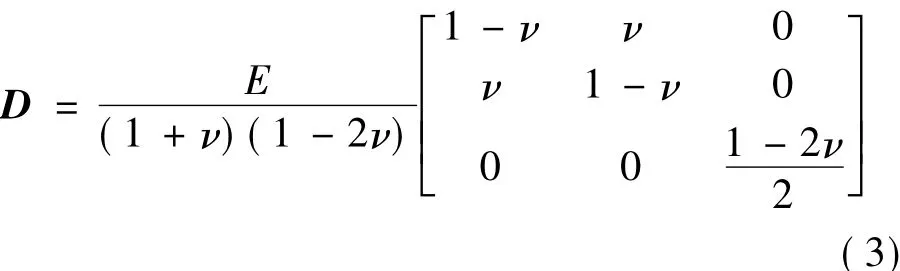
随着对磁性材料中磁致伸缩效应研究的广泛深入，研究者们所提出的磁致伸缩本构关系也不仅限一种。假定定子硅钢片中的磁致伸缩效应是各向同性的，并用等效节点力来模拟磁致伸缩力。利用有限元分析方法对电机进行单元剖分，则每个单元节点在磁场的作用下，由于磁致伸缩效应在节点处产生磁致伸缩力。当定子硅钢片受到磁场的作用时，由于磁致伸缩效应产生的应变是由平行于磁场方向和垂直于磁场方向上的应变组成，此时应力与应变的之间关系应用的是胡克定律，其表达式如下［8］:

式中:σ为应力;α为材料常数;ε为应变;εP为平行于磁场方向上的应变变;εv为垂直于磁场方向上的应变;ν为泊松比;E为杨氏模量。

假设在剖分单元ie上的等效节点ip上磁致伸缩力和位移分别为fip和uip。在单元上的节点的ip位移示意图如图2所示。则在单元节点上的位移和

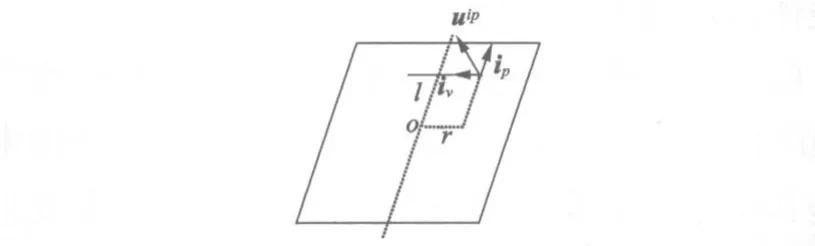
图2 等效节点位移示意图

磁致伸缩力:

式中:K为刚度矩阵，iv为垂直于磁场强度的单位矢量，ip为平行于磁场强度的单位矢量。

第三种磁致伸缩本构方程是从硅钢片被磁化的角度来研究。在二维电机中主要研究电机定子齿径向和垂直于径向方向上的磁致伸缩。它在任意方向的磁致伸缩量的表达式如下［9］:

式中:λi为i方向上的磁致伸缩量;λs为磁致伸缩常数;Mi为i方向上磁性材料的磁化强度;Ms为磁性材料的饱和磁化强度项表明当没有任何磁场存在的情况，磁性材料中的磁矩是随机取向的。当假设的材料有足够的预应力，使得所有的磁矩都垂直于磁化过程开始时的磁场方向时可以将式(9)中的忽略掉，从而简化为下式:

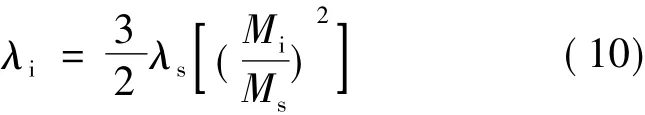
应用以上3种不同的磁致伸缩本构方程来仿真永磁电机在变化的磁场作用下，定子硅钢片受磁致伸缩效应影响的磁通密度、应力和应变。在电机图中分别选取定子齿根部、齿顶部的几个点来研究相关参量。通过比较这3种本构方程作用下的结果，得出几种不同本构方程的异同和对结果产生的影响。

2 结果分析

应用3种本构关系方程式对永磁电机仿真得到的0．01 s时的磁通密度结果分布图和采样点13在0～0．005 s处的3种本构关系下参考点的磁通密度B1，B2，B3分别如图3和表2所示。

图3 永磁同步电机磁通密度分布图

应力在0～0．01 s之间的磁致伸缩力密度均值如表3所示。

表2 采样处0～0．005 s时的磁通密度

表3 样点磁致伸缩力密度均值

通过对比3种本构关系下的磁通密度图和采样处0～0．01 s时的磁通密度值表明:应用3种不同的磁致伸缩本构关系仿真得出的电机的内部磁通密度的分布及大小并无太大的差别。同时也可以直观地看到在电机中磁通密度模值较大的部分是定子硅钢片的定子齿部。因此磁致伸缩效应引起的应力较大的分布位置主要是在定子齿根部、齿顶部的部位。

另外，通过仿真还得到了8个参考点处随时间变化的磁致伸缩力密度时域图，以及样点13处0～0．02 s之间的位移数值大小。由此可以了解电机磁致伸缩力随时间变化的大小、规律和位移大小。应用3种本构关系仿真得到的磁致伸缩力密度随时间变化的时域图和位移数值如图4、表4所示。

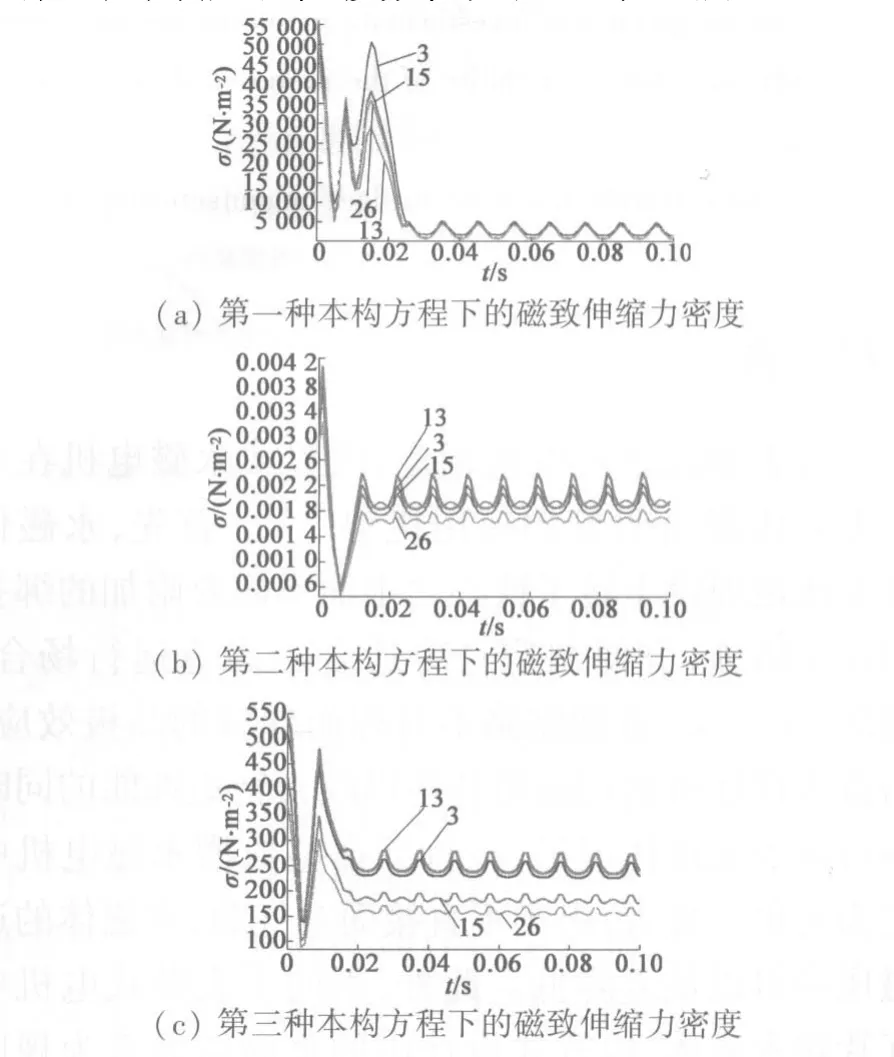
图4 永磁同步电机磁致伸缩力密度

表4 样点13 3种本构方程下的位移数值

通过对应力密度均值的对比分析可知，电机定子硅钢片在磁场的作用下定子齿根部的应力模值要大于齿顶部的应力模值，因此由磁致伸缩效应引起的应力会导致电机定子硅钢片的振动和形变。了解磁致伸缩效应对电机产生的应力，并由此引起的振动对解决电机中振动噪声问题提供了研究的方向。

通过数据比较得出：应用不同的磁致伸缩本构方程仿真得出的应力的变化频率随时间基本成周期性变化关系，而且变化的频率约为供电频率的2倍关系，且在大约100 Hz处达到最大值。并且，3种本构方程下的电机应力和位移数值大小却有着数量级的差异。经对比分析发现，利用线性压磁方程得到的振动位移数据与从磁化角度得到的数据较为接近。

3 结 语

应用不同磁致伸缩本构方程仿真得到的电机磁通密度的大小及分布大体上是相同的，而且都表现出来的是在定子的齿根部和齿顶部磁通密度比较大。

结果表明，永磁电机受磁致伸缩效应影响产生的应力和应变主要是定子齿根部和齿顶部较大。而且应力的变化的频率是电机供电频率的2倍。且齿根部的应力模值大于齿顶部应力模值。3种方程所得出的磁通密度的模值及分布无明显差别，而应力、位移的模值却有着数量级的差异。且线性压磁方程下得到的数据与先前研究者们实验条件下得到的磁致伸缩数据更为接近，考虑电磁－机械之间的相互耦合使预测的结果更接近于实际。通过对不同本构方程的研究为预估分析电机中由磁致伸缩效应引起的应力、应变等提供了合适的耦合方程与方法。

［1］ 祝丽花，杨庆新，闫荣格，等．考虑磁致伸缩效应电力变压器振动噪声的研究［J］．电工技术学报，2013，28（4）：1－7．

［2］ 刘鸣，景建方．降低电机噪声的方法研究［J］．船电技术，2011，31（12）：21－24．

［3］ BELA HCEN A ．Vibr ation of r otating electrical machines due to magnetomechanical coupling and magnetostriction ［J］．IEEE Tr ansactions on Magnetics，2006，42（4）：971－974．

［4］ SOMKUN S，Anthony J．Moses，Philip I．Anderson．Ef f ect of magnetostriction anisotr opy in Nonoriented electrical steels on def or mation of Induction motor stator cores［J］．IEEE Tr ansactions on Magnetics，2009，45（10）：4744－4747．

［5］ 韩雪岩，张哲，吴胜男，陈健．考虑磁致伸缩效应永磁电机的振动噪声研究［J］．电工电能新技术，2015，34（1）：28－34．

［6］ 张艳丽，李强，王洋洋，等．谐波磁场下硅钢片磁致伸缩特性分析［J］．电工技术学报，2015，30（14）：544－549．

［7］ 张艳丽，孙小光，谢德馨，等．无取向电工钢片磁致伸缩特性测量与模拟［J］．电工技术学报，2013，28（11）：176－182．

［8］ GAO Yanhui，MURA MATSU K，et al．Vibr ation anal ysis of a reactor driven by an inverter power suppl y considering electro magnetism and magnetostriction ［J］．IEEE Tr ansactions on magnetics，2009，45（10）：4789－4792．

［9］ ZHANG Xin，YANG Qingxin，ZHANG Xian．Nu merical anal ysis of stress in the l ar ge per manent magnet motor stator cores incl uding magnetostriction ef f ects［J］．Inf or mation Technology Jour nal，2013，12（12）：8235－8241．