基于DWT和RNN的无刷直流电动机轴承故障检测方法
2017-06-13庄夏
庄 夏
(中国民航飞行学院科研处,广汉618307)
0 引 言
无刷直流电动机(以下简称BLDCM)具有结构简单、调速快、效率高等优点,在航空、航天工业中广泛应用。然而,它也时常会出现故障情况,其中电机轴承故障约占电机故障的40%左右[1]。为了保证飞行器的安全并避免电机严重失效,对电机轴承故障进行早期检测具有重要意义。
目前,电机轴承故障检测技术主要分为3类:基于信号、基于知识和基于模型技术[2]。其中,基于信号分析的故障检测技术较为实用,其一般是对电机的定子电流信号、转矩谐波信号或轴向振动信号等特征信号进行时域和频域分析[3],找出各种故障发生时的时频域特征来检测故障。最常用的频域分析方法有快速傅里叶变换(以下简称FFT)。然而,FFT没有考虑电机的非线性和非稳定的运转方式,且由于大功率噪声的存在,其很难从频谱中获得轴承故障信号。为此,形成了多种先进的频谱分析方法,例如高分辨率光谱分析、小波变换和Park矢量分析等[4]。其中,离散小波变换(以下简称 DWT)是对小波变换中的尺度和平移进行离散化[5],能够很好地对非平稳信号进行自适应时频分析。
对于模式识别技术,常用的有神经网络、支持向量机等。然而,传统神经网络存在收敛速度慢、分类时间长等缺陷。带偏差单元的递归神经网络(以下简称RNN)[6]是利用网络内部状态的反馈来描述系统的非线性行为。其反馈节点可以存储先前信息,偏差单元可以将经验知识引入到网络学习过程中,能够有效提高网络的学习效率。
基于上述分析,本文提出一种用于电机轴承故障检测的鲁棒方法,主要创新点:(1)采用电机振动信号和电流信号共同作为特征源,以此提高故障检测的准确性。(2)利用DWT对信号进行时频分析,由于采用了2个信号源,所以特征数量较多。因此,在考虑信号具有非平稳、非线性特性下,采用了一种新型的特征降维方法:线性局部切空间排列算法(以下简称LLTSA)来选择出高效特征。(3)采用了带有偏差单元的RNN作为故障分类器,以此提高分类精度。
1 提出的故障检测方案
电机轴承故障一般表现为外圈缺损、内圈缺损和滚珠缺损。在发生故障时,会产生周期性的冲击振动。另外电机稳态定子电流信号也会有因转动不平衡而发生变化,能够描述电机的动态特性。为此,本研究利用电流传感器采集电机电流信号,利用加速度计采集电机振动信号,通过对这2种信号的分析来检测故障。
提出的故障检测方案总体框架如图1所示。主要包含4个步骤:(1)电机定子电流和振动信号的采集;(2)基于DWT的特征提取;(3)基于LLTSA的特征降维;(4)基于RNN的故障分类。
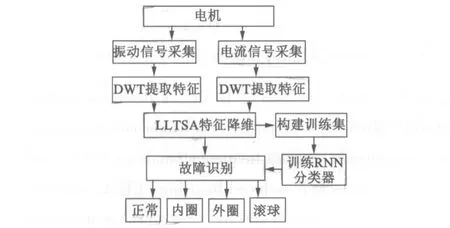
图1 提出的故障检测流程图
1. 1基于DWT的特征提取
当轴承出现局部缺陷时,若电机的转速恒定,则该缺陷部分会产生一个固定时间间隔的重复脉冲信号,该重复频率称为故障特征频率。然而,现实场景中,轴承经常工作在变速和变负载的非平稳条件下,致使脉冲不会严格按照周期性出现。这样,传统的包络分析特征提取方法已经不再适用。目前,电机信号的特征提取通常是对信号进行时域、频域和时频域分析而获得。其中,基于FFT的频域分析对非平稳信号不适合。另外,对所有频率执行短时傅里叶变换(STFT)也会受到窗口宽度恒定和计算量大的限制。
小波变换能够探索信号的局部特征,且能够对不同时间分辨率和频率分辨率的信号进行分析。小波变换可表示如下:

式中:c(n)为尺度因子;d(j,n)为小波系数,表达式如下:

离散小波变换(以下简称DWT)是小波变换的离散形式,已经成功应用于故障检测和定位中,且计算时间比其他信号处理技术有显著减少。DWT的层次结构如图2所示。在每个层次中,使用低通滤波器 g[n]和高通滤波器 h[n]将原始信号Ao(k)分解成细节成分dj和近似值an。其中,细节成分即高频成分,近似值即低频成分,这些与小波变换的缩放和移动因子相关。
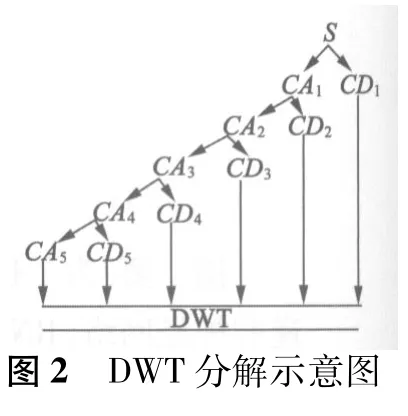
在每层的缩放和移动中,信号和小波分析之间的相关性称为小波系数。信号的分辨率是信号中细节信息数量的度量,可以通过滤波器来调节。另外,缩放因子可以通过改变窗口函数尺寸来调整。由DWT分解得到的一组小波信号dj和近似值aj可以描述:

DWT中的小波母函数的选择影响着时域和频域上的信号分辨率。为此,本研究通过反复试验,最终选择 Deubechies(db2,db4,sym4,coif2)作为母函数。另外,根据文献[7]的研究成果,发现其中的db4小波对电信号的瞬态行为检测较为合适。为此,本研究使用db4作为原始母小波,将信号划分为6 个频段,即5 个细节分量(d1,d2,d3,d4,d5)和一个近似分量(a1)。表1给出了各分解层次以及所对应的频带。
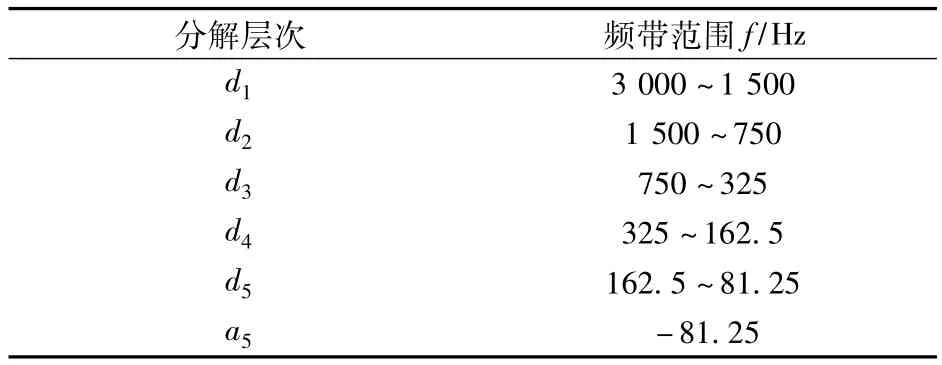
表1 小波频带
在频段分解后,计算出各频段的信号能量作为特征。表2给出了实验中BLDCM在空载且转速为1200 r/min时,正常和故障状态下,电机振动信号DWT后各频段的信号能量。可以看出,不同状态下的各频段的能量具有明显差异。

表2 振动信号的小波能量(W/J)
1. 2基于LLTSA的特征降维
经过对两个信号(电流和振动)DWT后,共产生12个特征。如果将这些特征全部输入到RNN分类器中,将会大大增加分类器的计算量,且由于一些分辨能力较差特征的融入,也会影响分类器的正确识别率。为此,需要进行特征降维,提取出具有高分辨能力的特征。
目前,比较成熟的降维方法主要为一些全局线性降维方法,例如主成分分析(以下简称PCA)、线性判别分析、多维尺度分析等[8]。然而,电机故障信号是非平稳、非线性的,其信号特征为时变特性。所以,这些传统方法不能很好地应用在电机故障检测中。
近年来,一些学者将非线性流形学习方法[9]应用到非线性数据降维中,取得了良好效果。其中,典型的为局部切空间排列算法(以下简称LTSA)。然而,LTSA假定数据局部是线性的,对于高曲率的电机故障信号具有局限性。为此,本研究采用最新的线性局部切空间排列算法(以下简称LLTSA)[10]。LLTSA在LTSA算法上融入了PCA过程,通过数据集中样本点邻域的低维切空间来描述数据的流形局部结构,然后利用局部切空间排列来构建全局低维坐标。
LLTSA降维的主要步骤如下:
步骤1:构造邻域。令特征提取过程中获得的特征向量为 X={x1,x2,…,xN},N 为原始特征数量。对于每个特征xi,根据欧式距离,通过K-邻近(以下简称KNN)方法从其邻域中选择出k个近似点 Xi=[xi1,…,xik]。
步骤2:局部信息提取。在邻域Xi中找到一组‖XiHk-QiΩi‖2,以此获得邻域的结构信息。其中,Hk为中心化矩阵。
步骤3:局部切空间全局排列。对特征集的本征结构进行重构,其可表示为一个最小化近似求解中,Yi为Xi的全局低维坐标,Li为局部转换矩阵。
步骤4:构建映射矩阵。将上述问题转换为广义特征值和所对应特征向量的求解过程:X HNB HNXTα = λX HNXTα。其中,B=SVVTST;B 为全局排列矩阵,S为选择向量,V=Hk(I-Θi)。将前d个广义特征值对应的特征向量组成映射矩阵为 A= [α1,α2,…,αd],即从高维空间到低维空间的映射矩阵。那么,原始数据集X降维后获得的低维全局坐标为Y=ATX Hk。
在后续的RNN分类器中,其分类时间与输入特征数量直接相关。在综合考虑故障检测性能和检测时间下,本研究设定用于故障检测的特征数量为4,即对初始特征进行LLTSA降维后,输出前4个具有高分辨率的特征。为了验证特征降维的效果,对于所降维后的特征,计算其在各故障类特征集中的类间和类内距离。结果发现,所获得的特征都具有较大的类间距离和较小的类内距离,证明了特征降维的有效性。
1. 3基于RNN的故障分类
RNN包含了反馈结构和偏差单元,比前馈神经网络具有更高的学习能力。在本文中,采用RNN中的非线性含输入自回归(NARX)模型[11],来对非平稳操作下的轴承故障进行检测和分类。NARX模型中,其输出会通过一条延迟线反馈给输入。
本研究中,RNN由输入层、一个隐藏层和输出层组成,如图3所示。
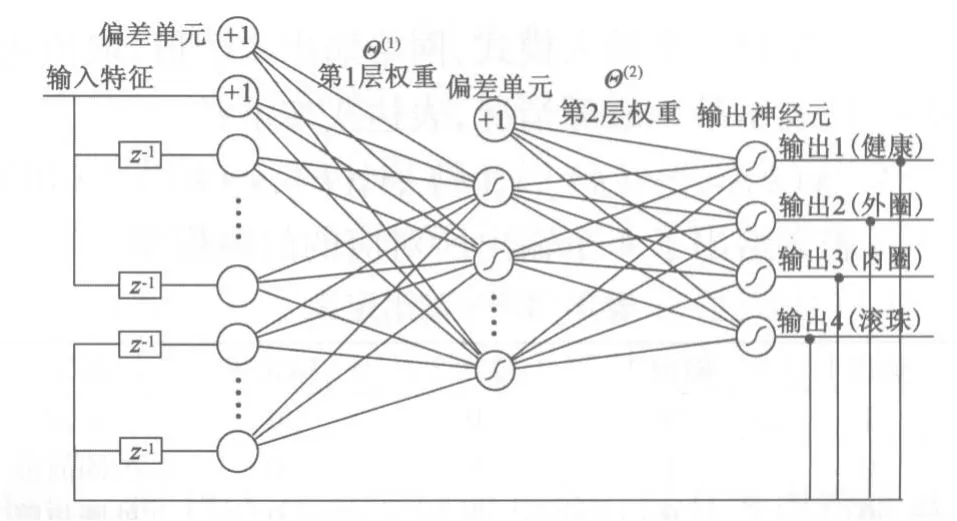
图3 用于故障检测RNN结构模型
由上述特征提取和降维后,获得4个LLTSA特入。输出层有4个神经元,用来表示特定的轴承故障状况。那么,网络在每个时间点k处的输入模型(输入层)由4个输入特征和4个输出反馈组成,表示如下:

式中:ndij和ndoj分别为输入特征i和输出反馈j的延迟量。输入和输出延迟分别用于所有输入和输出特征。另外,神经网络的隐藏层和输出层采用sigmoid激活函数。对于每一个输入模式x(k),每个节点的输出由前向传播计算获得,表达式如下:
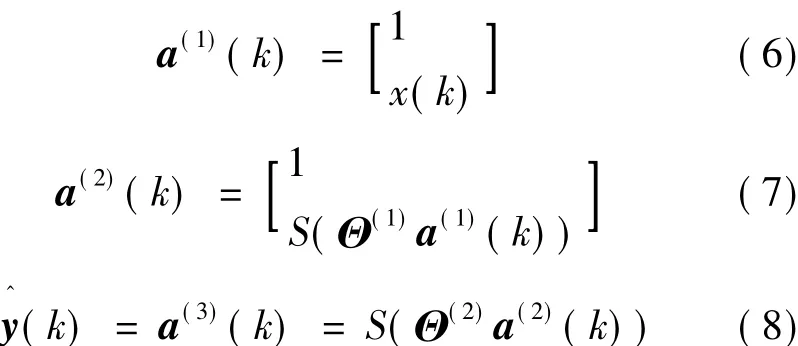
式中:表示第l层第i个神经元的激活输出;为神经网络的输出向量;Θ(1)和Θ(2)为神经网络的参数矩阵;表示第l层第j个神经元与第l+1层第i个神经元之间的连接强度;S(x)为sigmoid激活函数,表达式如下:
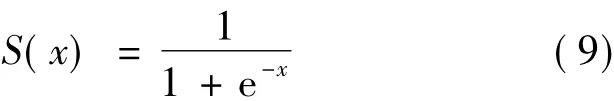
对于每一个输入模式,网络输出4个值,取值为0或1,表示某一故障情况,表达式如下:
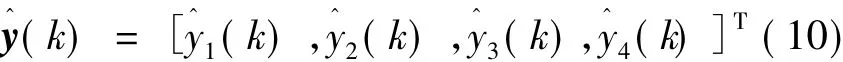
表3给出了4个输出所对应的故障模型。
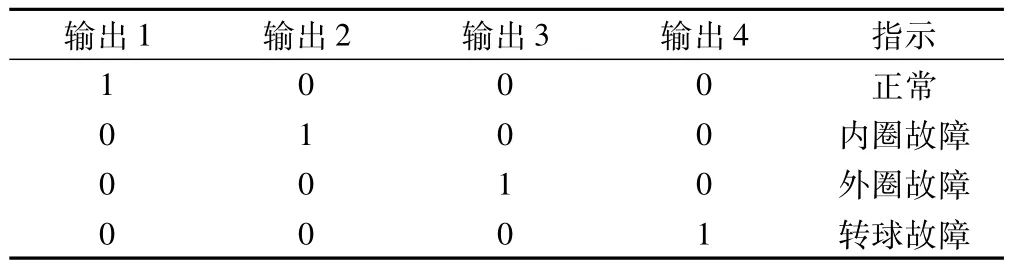
表3 RNN输出定义
为了训练神经网络,将数据集中每种故障数据的60%作为训练数据。训练目标为最小化成本函数J,表示如下:
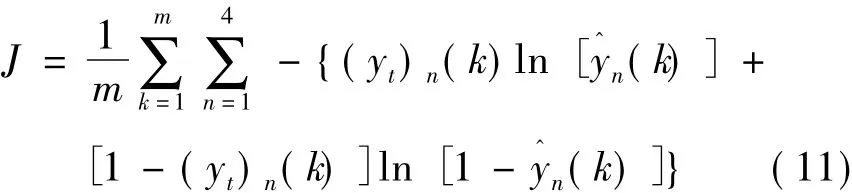
式中:m为训练样本的数量;yt为每个样本的目标输出。训练过程通过递归执行梯度下降法实现,表示如下:

式中:为学习速率,在初始时随机抽取。为了计算梯度,使用BP算法,步骤如下:
对每个训练模式想x(k):
1)根据式(6)~式(8)获得a(l)(k),a(2)(k)和y^=a(3)(k)
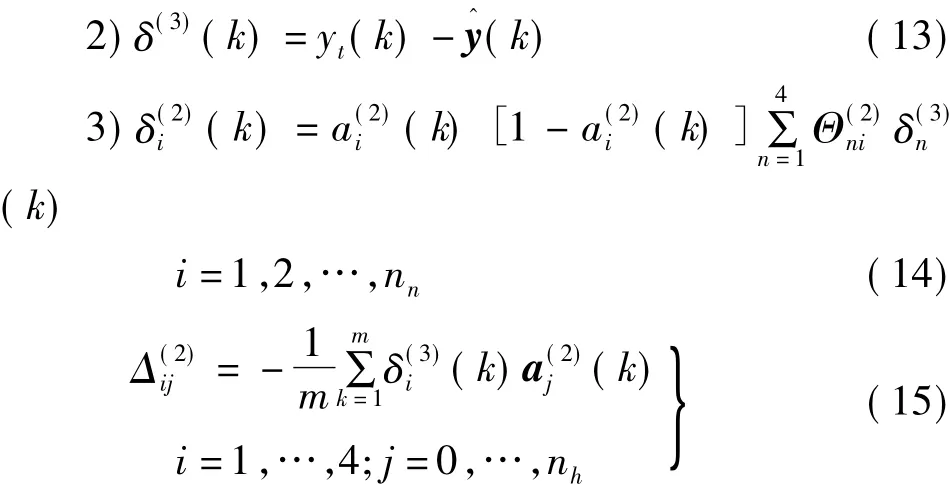
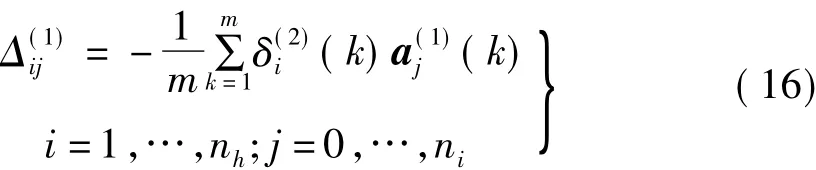
式中:nh为隐层神经元数量(不包括偏差单元);ni为输入层神经元数量(不包括偏差单元)。
2 实验及分析
2. 1 实验设备
实验中电机和负载装置如图4所示,电机为一个额定功率为100 W,额定电压为24 V,额定转速为1 500 r/min的三相无刷直流电动机BLDCM;将一个永磁直流发电机与BLDCM级联作为负载,并使用变阻器连接到永磁发电机,用来调节负载大小。将一个满刻度为±5 g,带宽为0.5~1 600 Hz的三轴加速度计ADXL325安装在电机输出轴上,用来采集振动信号。此外,通过一个电流传感器ACS714来采集电机定子电流。将传感器输出的数据通过一个采样率为3 kHz,一次采样时间为30 s的模数转换器(NI usb-6009)转换成数字信号,并送到PC机中用来后续处理。

图4 电机和负载装置
另外,电机中的轴承为一个型号6000ZZ的滚珠轴承,滚珠直径为3 mm,轴承外圈直径为25 mm,内圈直径为14 mm。轴承故障分为内圈故障、外圈故障和滚珠故障,如图5所示。

图5 轴承故障
2. 2 数据采集
在4种状态(正常、内圈、外圈和滚珠故障)下运行并记录振动和电流数据。其中,每个测试都会在3种不同的恒定速度(600 r/min,900 r/min和1200 r/min)和3种不同的负载(空载、半载和满载)下进行测试。因此,共进行了24个不同测试,以此完整记录正常和异常情况下的电机数据。
为了展现负载对电机信号的影响,设定电机在0~15 s内空载运行,在第15 s时刻处对电机施加一个负载,在正常和不同轴承故障状态下采集振动信号和电流信号,结果如图6所示。其中,图6(a),图6(b)为正常情况下的时序波形,图6(c)~图6(h)分别为在轴承内圈故障,外圈故障和滚珠故障情况下的时序波形。通过观察发现,在相同负载情况下,存在故障时的振动信号波形的幅度要比正常情况下大很多。当负载增加时,振动信号波形的能量也会相应增加,即平均幅度增加。在不同状态下,电机定子电流信号也具有明显差异性,因此,振动信号和定子电流信号能作为故障检测的有效依据。

图6 各种故障状态下的电机振动信号和电流信号
2. 3 性能比较
分别采集400组电机振动和电流信号,其中每种状态(正常、外圈故障、内圈故障和滚珠故障)下各采集100组。将60%的数据作为训练数据来训练RNN,其余40%作为测试数据。
为了验证所采用的LLTSA特征降维方法的有效性,将其与典型的PCA方法进行比较。其中,特征提取和故障分类方法都相同。在空载且不同电机转速下的比较结果如表4所示,在转速为1 200 r/min且不同负载下的比较结果如表5所示。其中,实验数据为5次单独实验的平均值。
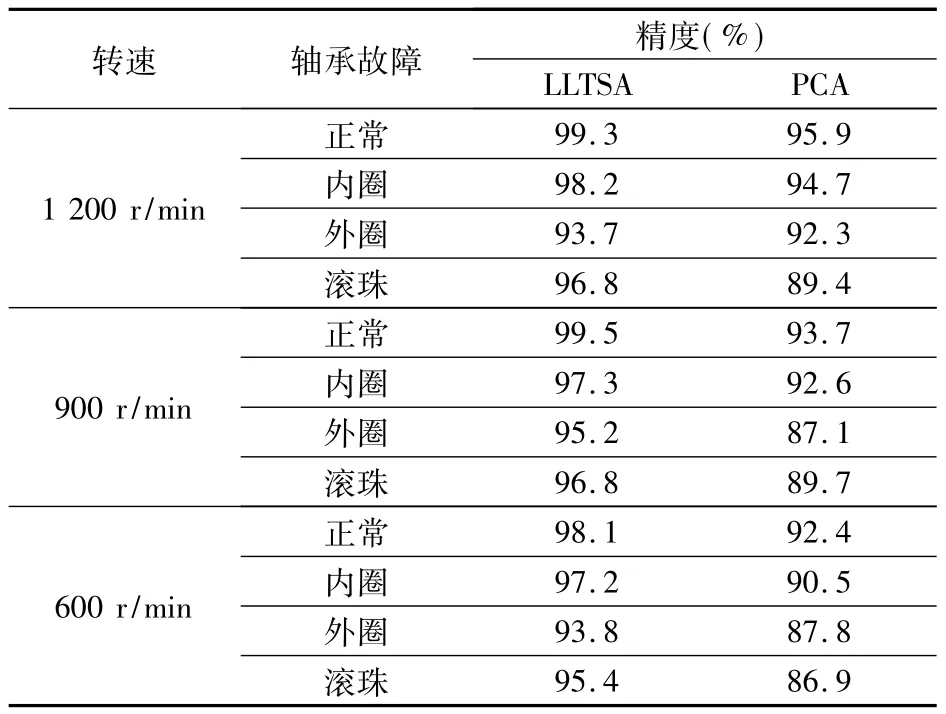
表4 不同转速下的故障检测精确度
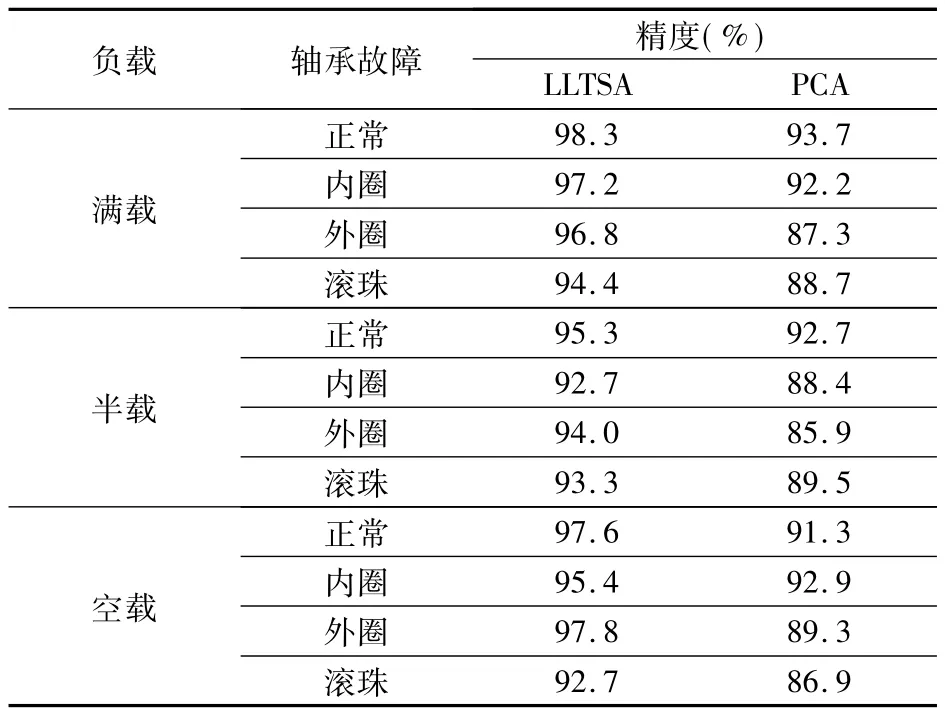
表5 不同负载下的故障检测精确度
可以看出,在不同转速和负载条件下,与PCA技术相比,采用LLTSA技术的故障检测系统的整体检测精度较高,平均识别率达到了96.1%,比PCA的90.5%提高了约5.6%,这证明了特征降维技术的优劣对整个系统具有较大影响。这是因为LLTSA技术在特征降维过程中考虑了特征的非平稳性和特征之间的相关性,获得了能够更好表征故障特性的特征。而PCA在减少特征冗余时没有考虑特征或变量与特定类标签之间的关系,影响了检测精度。
另外,可以看出,在不同转速和负载下系统的检测率变化不大,这证明了提出的检测方法对转速和负载变化具有较好的鲁棒性。
为了进一步验证提出的整个故障检测系统的有效性,将其与现有的几种主要方法进行比较。分别为文献[12]提出的基于统计特征+PCA降维+静态NN分类器的检测系统;文献[13]提出的基于连续小波变换(CWT)+支持向量机(SVM)分类器的检测系统;文献[14]提出的基于CWT+模糊逻辑系统(FLS)的检测系统。文献[15]提出的基于经验模态分解(EMD)+前馈神经网络(FFNN)分类器的检测系统。比较结果如表6所示。可以看出,提出的方法的平均故障检测率最高,达到了96%。这是因为同时采用了振动信号与电流信号作为特征源,采用DWT和LLTSA获得了精简且有效的时频域特征,并通过DNN实现了高精度分类。另外,系统的故障检测平均时间约为0.4 s,符合实时检测要求。
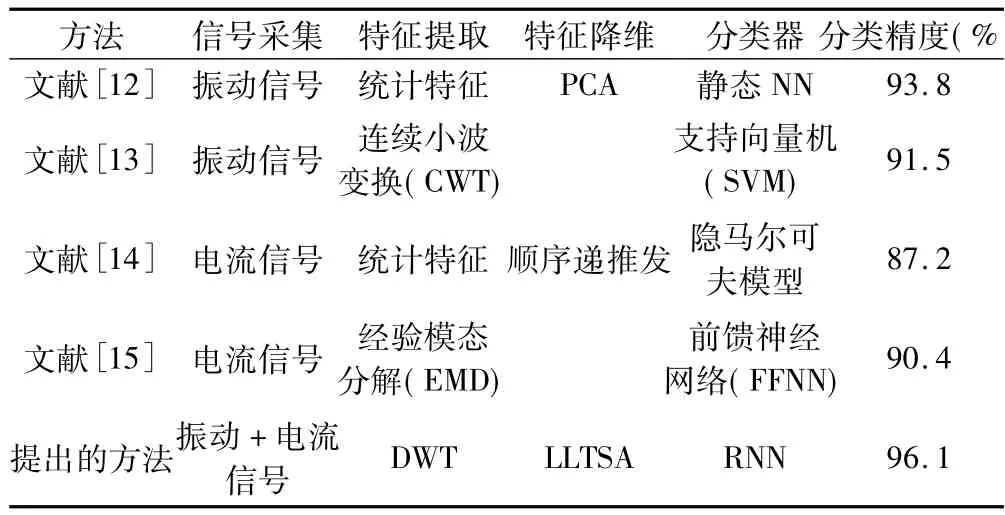
表6 提出的方法与现有方法的比较
3 结 语
由于实际场景中的电机转速和负载可能存在非平稳性,这对电机轴承故障的检测增加了困难。为此,提出了一种用于DLBCM的鲁棒轴承故障检测技术。通过对电机定子电流和振动信号进行DWT分析来提取特征,然后通过LLTSA特征降维和RNN分类器来检测并识别故障类型。实验结果表明提出的检测方法能够准确检测轴承故障,并对电机转速和负载具有鲁棒性,具有较高的实用价值。
[1] 杨江天,赵明元.改进双谱和经验模态分解在牵引电机轴承故障诊断中的应用[J].中国电机工程学报,2012,32(18):116-122.
[2] KONAR P,CHATTOPADHYAY P.Bearing fault detection of induction motor usingwavelet and Support Vector Machines(SVMs)[J].Applied Soft Computing,2011,11(6):4203 - 4211.
[3] 李珂,邰能灵,张沈习.基于小波包熵和概率神经网络的微特电机轴承故障监控[J].微特电机,2016,44(4):37 -39.
[4] SINGH S,KUMAR N,KUMAR A.Motor current signature analysis for bearing fault detection in mechanical systems[J].Procedia Materials Science,2014,6(6):171 -177.
[5] 毛永芳,秦毅,汤宝平.过完备有理小波变换在轴承故障诊断中的应用[J].振动、测试与诊断,2011,31(5):626 -630.
[6] 杨秋英,陈卉.带偏差单元递归神经网络齿轮箱故障诊断[J].现代电子技术,2013,36(20):33 -37.
[7] SAFAVIAN L S,KINSNER W,TURANLI H.Aquantitative comparison of different mother wavelets for characterizing transients in power systems[C]//Canadian Conference on Electrical& Computer Engineering.IEEE,2005:1461 -1464.
[8] 王成.基于谱正则化的线性降维方法研究[D].南京:南京理工大学,2012.
[9] 栗茂林,梁霖,王孙安,等.基于连续小波系数非线性流形学习的冲击特征提取方法[J].振动与冲击,2012,31(1):106-111.
[10] 苏祖强,汤宝平,邓蕾,等.有监督LLTSA特征约简旋转机械故障诊断[J].仪器仪表学报,2014(8):1766-1771.
[11] ANGM R CO,GONZALEZ R M,CASTROPPM.Multiple data fusion for rainfall estimation using a NARX-based recurrent neural network - the development of the REIINN model[J].2014,17(1):682 -691.
[12] PRIETO M D,CIRRINCIONE G,ESPINOSA A G,et al.Bearing fault detection by a novel condition-monitoring scheme based on statistical- time features and neural networks[J].IEEE Transactions on Industrial Electronics,2013,60(8):3398 -3407.
[13] KANKAR P K,SHARMA S C,HARSHA S P.Fault diagnosis of ball bearings using continuous wavelet transform[J].Applied Soft Computing,2011,11(2):2300 -2312.
[14] 董磊,周灏,潘龙飞,等.由定子电流信号分析陀螺电机滚珠轴承故障诊断与分类(英文)[J].中国惯性技术学报,2015,23(3):415-420.
[15] CAMAREMARTINEZ D,VALTIERRARODRIGUEZ M,GARCIAPEREZ A,et al.Empirical mode decomposition and neural networks on FPGA for fault diagnosis in induction motors.[J].Scientific World Journal,2014,24(1):140-147.
