海上风力发电机桶形基础竖向初始动阻抗影响因素分析
2017-06-13郑金海
林 捷,贺 瑞,郑金海
(1.河海大学港口海岸与近海工程学院,江苏 南京 210098;2. 河海大学海岸灾害及防护教育部重点实验室,江苏 南京 210098)
海上风力发电机桶形基础竖向初始动阻抗影响因素分析
林 捷1,2,贺 瑞1,2,郑金海1,2
(1.河海大学港口海岸与近海工程学院,江苏 南京 210098;2. 河海大学海岸灾害及防护教育部重点实验室,江苏 南京 210098)
利用ABAQUS大型通用有限元软件,建立弹性半空间中的海上风力发电机桶形基础(简称桶基)有限元模型。将数值解与已有解析解对比,验证桶基数值模型的准确性。并研究不同因素对桶基竖向初始动阻抗的影响,以及桶基与桶壁壳基础初始动阻抗的关系。结果表明,桶基长径比、桶基厚径比、土体泊松比、土体剪切模量、土体非均匀性对初始动阻抗影响明显,桶基材料对初始动阻抗影响不大;桶基和桶壁壳基础初始动阻抗基本重合,桶基可以退化为桶壁壳基础进行模拟。
海上风力发电机;桶形基础;竖向初始动阻抗;有限元分析方法
一直以来,由于海上风力发电机(简称风机)设计时难以准确计算基础动阻尼,导致风机设计太过保守,建设成本高。桶形基础(简称桶基)作为近海风机的基础形式主要包括单桶基础或多桶基础,它安装方便,成本低。随着海上风电开发水深的不断增大,从海上石油平台导管架结构演变而来的,适应水深范围更广、承载力更大的三脚架及四脚架等多桶基础被应用到风机的基础中。吸力桶基础作为这些“多足”支撑结构的每个“脚”形成多桶基础,通过竖向反力抵抗风机塔架的倾覆弯矩[1]。
初始动阻抗定义为极小应变时的动阻抗,类似于土动力学中的土体初始剪切模量G0。将桶基初始动阻抗研究清楚后,将有利于进一步研究桶基在外部荷载作用下的演化过程,精确计算正常运行状态下的动阻抗,为海上风机设计提供准确的刚度和阻尼参数。2014年Versteijlen等[2]发现实测风机的自振频率要高于设计值,这说明设计风机动阻抗偏小,并已着手开始研究小应变下的基础初始动阻抗。国内外对桶基进行了大量研究。Bhattacharya等[3]通过物理模型试验,研究了循环荷载作用过程中桶基自振频率和动阻抗的变化情况;Houlsby等[4-5]通过大比尺室外模型试验,测试了较高频率下,在砂土和黏土中模型桶基在动弯矩作用下的动阻抗; Liingaard等[6-7]通过耦合边界元-有限元方法研究了黏弹性半空间中桶基的动阻抗,同时通过实测海上风机塔架自振频率,反算得到桶基动阻抗;Versteijlen等[2]通过有限元法计算了弹性地基土小应变下桶基的初始刚度。贺瑞[8]将桶基简化为埋置在海床中的弹性薄壳或刚性薄壳,研究了基础的竖向、水平及摇摆耦合振动特性及影响因素。总的来说,国内外学者对桶形基础安装特性和极限承载力及其影响因素进行了大量的研究[9],但是对于桶基的竖向初始动阻抗研究很少,初始动阻抗的内在机理和影响因素亟待深入研究。本文通过有限元软件ABAQUS,建立起弹性半空间上的桶基有限元模型。经过大量的数值计算,分析桶基壁厚、桶基长径比、桶基材料、土体泊松比、土体剪切模量、土体非均匀性等因素对桶基竖向初始动阻抗的影响。

图1 桶基模型示意图Fig.1 Sketch of bucket foundation model
1 桶基竖向初始动阻抗
研究桶基埋置于理想的均匀弹性土体半空间上的竖向初始动阻抗。竖向集中力作用在桶基顶盖的中心。桶基半径为R,桶基桶壁长为L,桶壁厚度为t,如图1所示。
假定桶基的质量为m,桶基竖向初始动阻抗定义为作用在桶基上简谐荷载的值和相应简谐位移的比值,其值是复数,实部表示动刚度,虚部表示动阻尼。根据单自由度线性系统振动方程,可得
(1)
其中
Pv(t)=Pv0eiωtUv(t)=Uv0ei(ωt-φ)
式中:Pv——作用在桶基顶盖中心处的简谐激振力;k——系统刚度;Uv——简谐荷载作用下桶基竖向位移;c——系统阻尼;φ——桶基竖向振动和激振力的相位差;ω——激振力频率。
整理式(1),可得桶基竖向初始动阻抗表达式:

(2)
ABAQUS软件计算时考虑了桶基的密度和质量。由于动阻抗Kv的计算值往往达到10的n次方数量级,而式中mω2一项数值很小,对动阻抗计算值影响很小。为了计算方便,计算中将mω2一项忽略。桶基竖向初始动阻抗表达式又可写为
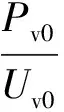
(3)
Kv表达式中的实部为桶基竖向动刚度系数kv,虚部为桶基竖向动阻尼系数cv。kv反映了土体的动刚度,cv反映了基础的能量损失和土体材料阻尼。即
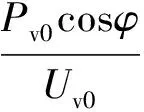
(4)
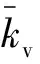
(5)

式(3)可改写为
(6)
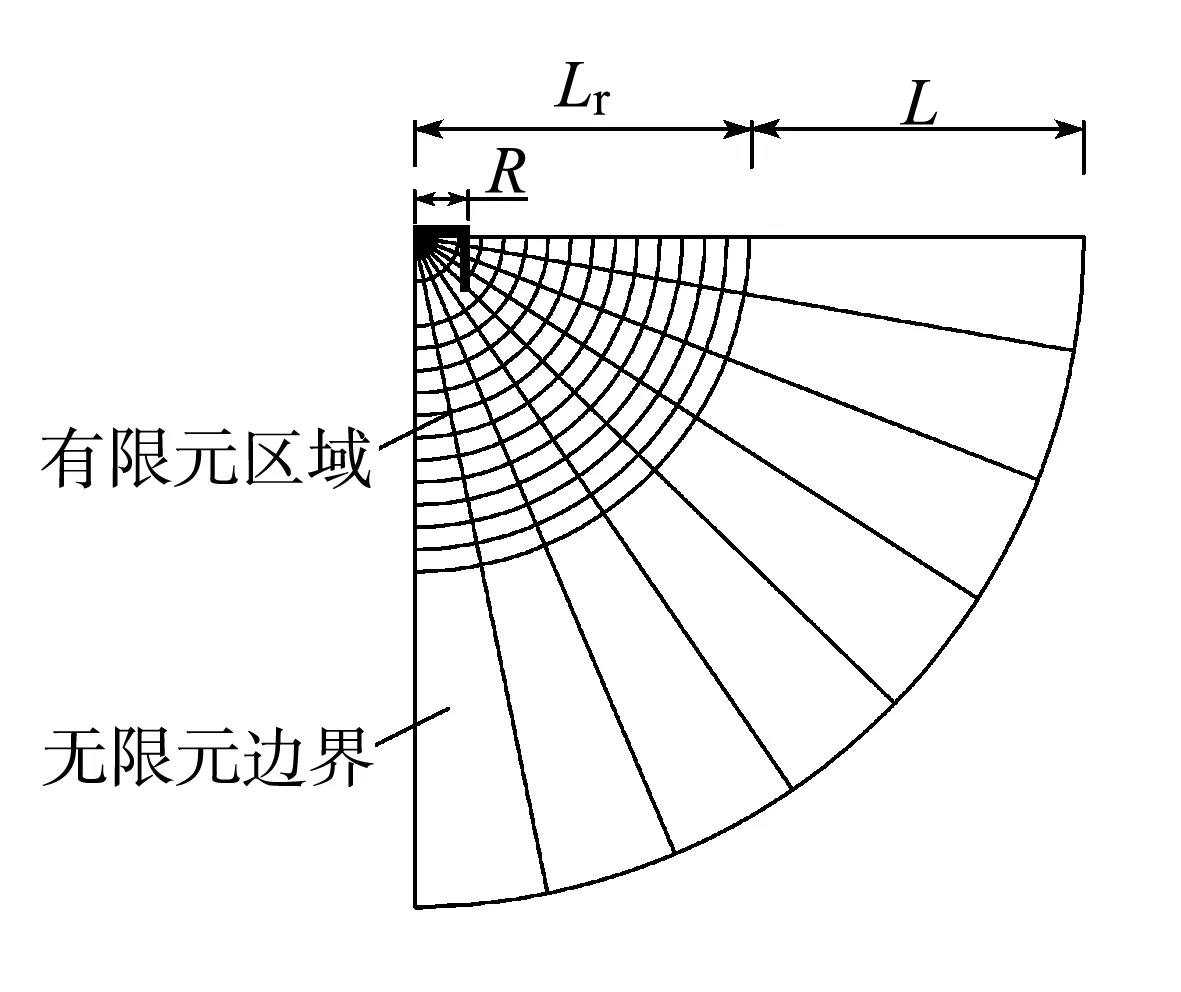
图2 有限元网格模型Fig.2 Finite element mesh model
2 有限元分析方法
2.1 有限元计算模型
由于桶基振动时会在土体中产生应力波,应力波传递到有限元模型边界后,反射回来,对模型计算结果的准确性会有很大影响,因此要选择合适的单元类型、边界条件和有限元土体的范围,才能使计算结果更加准确。有限元单元模型网格如图2所示。
为了准确模拟应力波在土体中的传播,土体有限单元尺寸受到土体剪切波长λ的影响。Kuhlemeyer等[10]和Lysmer等[11]提出单元最大尺寸lmax应该满足:
(7)
为避免应力波反射对计算结果产生影响,可在有限元区域外围设置吸收边界条件。黏滞阻尼边界条件[12]和无限元边界条件[13]是最常用的吸收边界条件。通过ABAQUS软件在有限元区域外面设置无限元单元边界条件,但是如果有限元区域不够大,仍会出现数值震荡。为了避免由于边界条件带来的误差,设置一个足够大的有限元区域[14]。该计算区域满足:

(8)
式中:Lr——有限元区域内应力波最短的反射距离;n——激振的周期数;ν——土体泊松比。
根据桶基结构和施加的荷载的对称性,选用ABAQUS轴对称边界条件。取桶基及土体的截面进行计算。土体和桶基都采用线弹性材料,有限元部分采用CAX4R单元,土体无限元采用CINAX4单元。桶壁和土体接触采用Tie接触,桶基顶部和土体接触法向采用硬接触,切向采用无摩擦接触,并在桶基顶部施加竖向均布简谐循环荷载,建立隐式动态分析步进行分析。
2.2 有限元计算
采用荷载控制法计算竖向动阻抗。在桶基顶部施加一个竖向的均布简谐循环荷载Pv。计算结束后,取桶基顶部土体所有节点的竖向位移进行平均;然后采用最小二乘法拟合位移曲线,求得位移公式Uv和相位差φ。将Pv0、Uv0和φ带入式(5),得到桶基竖向初始动阻抗。
3 桶基竖向动阻抗影响因素分析
3.1 ABAQUS模型验证

3.2 桶基及桶壁壳基础动阻抗关系
为了研究桶基和桶壁壳基础竖向动阻抗关系,在桶基和桶壁壳基础顶部施加单位竖向循环荷载。桶基半径R=5 m,顶盖厚度1 m,桶壁厚度t=0.05 m,长径比L/R=2。桶基弹性模量Ef=210 GPa,土体剪切模量为1 MPa,泊松比为0.33,密度为1 800 kg/m3。通过式(5)计算桶基和桶壁壳基础的竖向动刚度系数和动阻尼系数,如图4所示。
从图4可以看出,在无量纲频率a0∈[0,1]的范围内,桶基和桶壁壳基础的竖向动刚度系数和动阻尼系数基本重合,说明在研究竖向动阻抗时,桶基可以简化为壳基础进行模拟,如同贺瑞[8]所述。

图3 圆盘有限元模型竖向动阻抗和Luco等竖向动阻抗解析解比较Fig.3 Comparison of vertical dynamic impedance of circular foundation simulated by FEM with analytical solution of Luco et al. (1972)
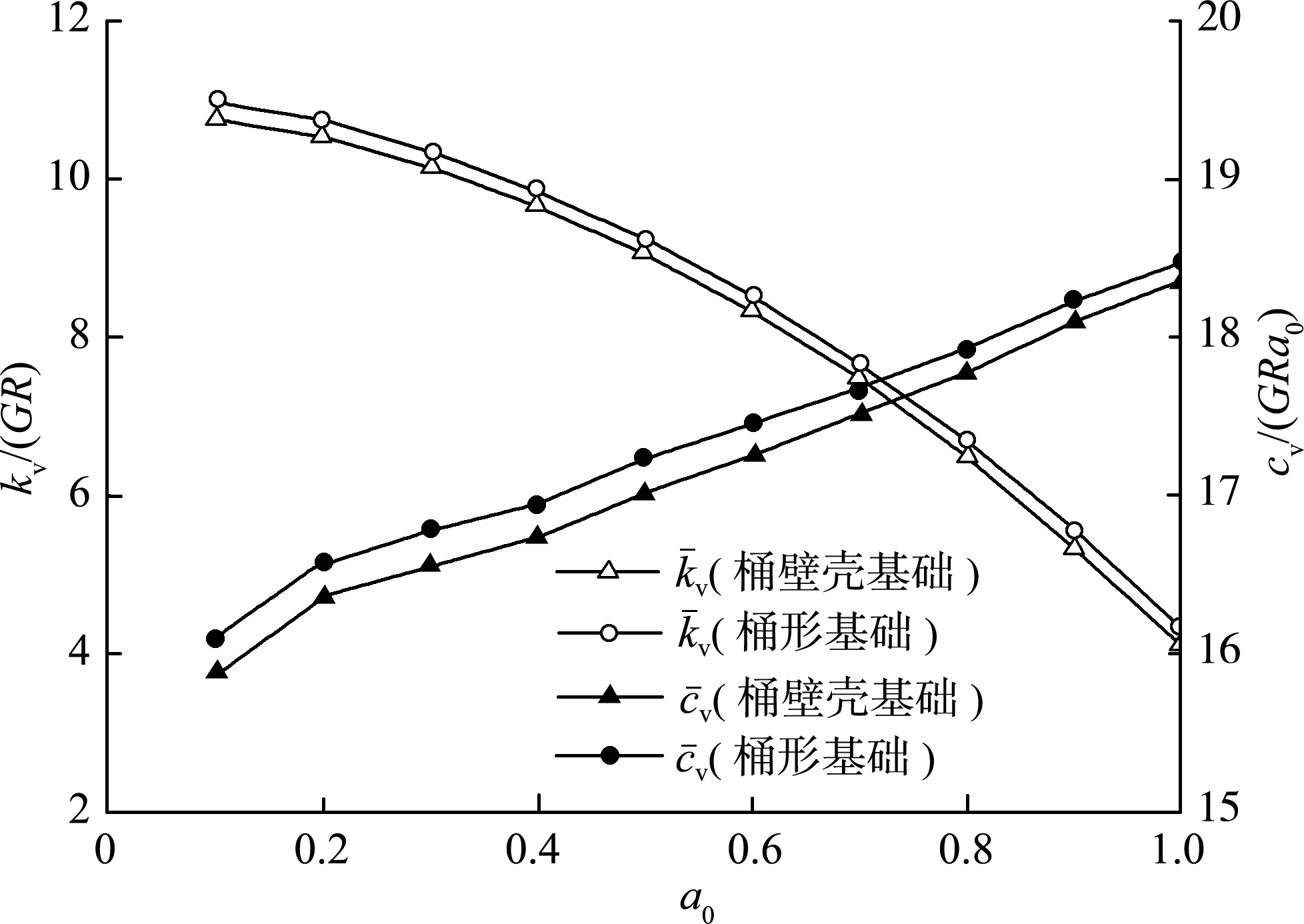
图4 桶基和桶壁壳基础竖向动阻抗比较Fig.4 Comparison of vertical impedances of bucket foundation and shell foundation
3.3 竖向初始动阻抗影响因素分析
影响桶基竖向初始动阻抗的因素很多,笔者设计了6组不同条件的桶基模型研究不同因素对竖向初始动阻抗的影响,计算a0∈[0,1]范围内桶基竖向初始动阻抗的变化情况,研究桶基厚径比(桶壁厚度与半径比值t/R)、桶基长径比(桶壁长度与半径比值L/R)、桶基弹性模量Ef、土体泊松比νs、土体剪切模量Gs、土体非均匀性等对桶基竖向初始动阻抗的影响。计算模型参数如表1所示。
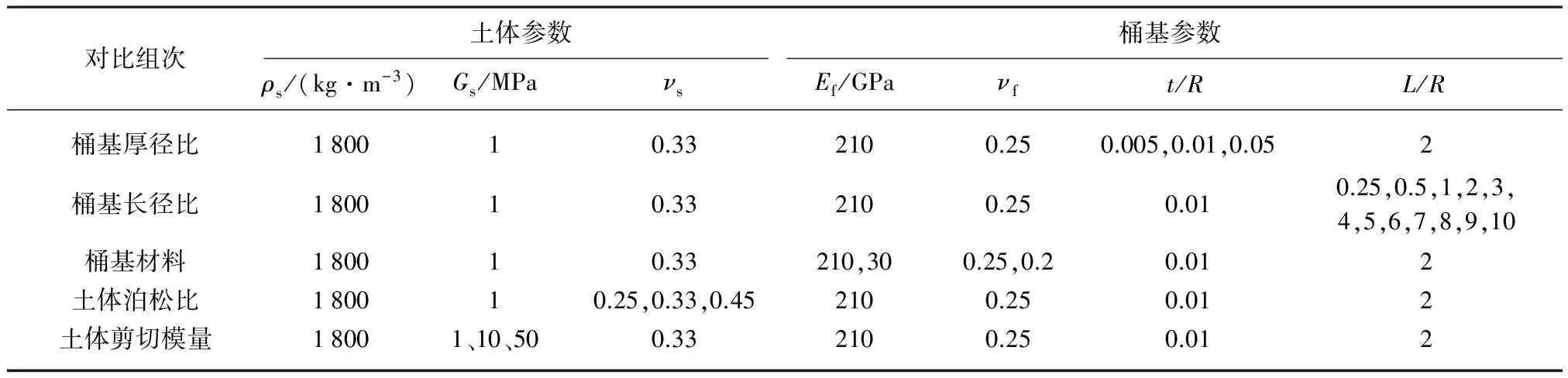
表1 计算模型参数
3.3.1 桶基厚径比影响

3.3.2 桶基弹性模量影响


图5 不同厚径比桶基竖向初始动阻抗Fig.5 Vertical initial dynamic impedance of bucket foundations with different thickness-to-diameter ratios

图6 不同材料桶基竖向初始动阻抗Fig.6 Vertical initial dynamic impedance of bucket foundations with different bucket materials
3.3.3 桶基长径比影响

图7 不同长径比桶基竖向初始动阻抗Fig.7 Vertical initial dynamic impedance of bucket foundations with different length-to-diameter ratios

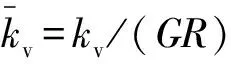
(9)
(10)
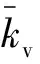
3.3.4 土体泊松比影响

3.3.5 土体剪切模量影响


图8 不同土体泊松比下桶基竖向初始动阻抗Fig.8 Vertical initial dynamic impedance of bucket foundations in different Poisson’s ratios of soil
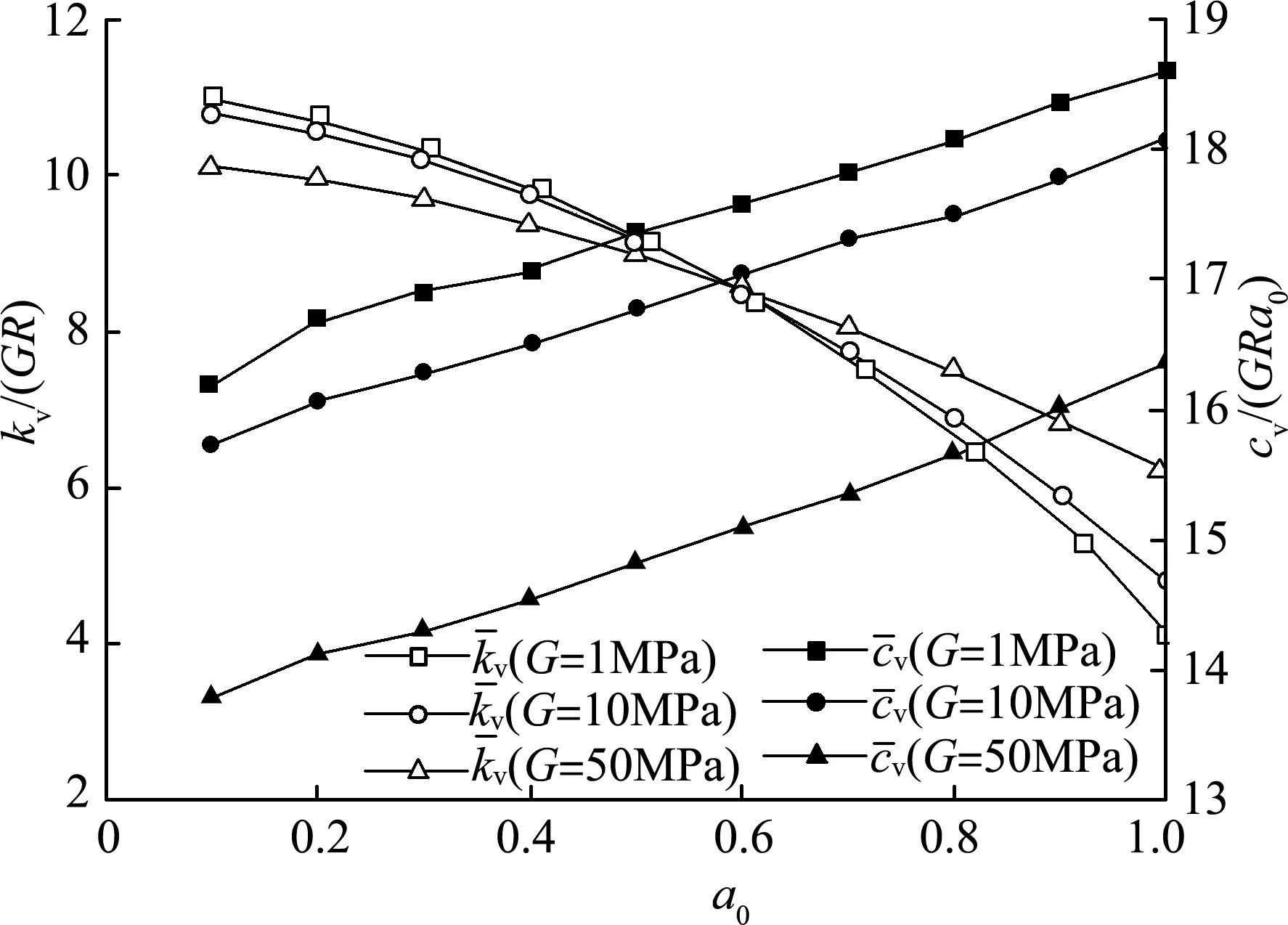
图9 不同土体剪切模量下桶基竖向初始动阻抗Fig.9 Vertical initial dynamic impedance of bucket foundations in different shear moduli of soil
3.3.6 土体非均匀性的影响
在实际工程中,土体的弹性模量往往随着深度的变化而变化。为了更好地研究实际情况下土体非均匀性对桶基动阻抗的影响,采用Gibson模型[18]。Gibson模型较好地描述了土体的非均匀性质,认为土体的剪切模量为随深度变化的线性函数。Gibson模型土体剪切模量公式为

图10 土体剪切模量随深度变化Fig.10 Variation of soil shear modulus with depth
G(z)=G0+bz
(11)
式中:z——土体深度;G0——土体在桶基半径R深处的剪切模量,G0=50 MPa;b——剪切模量随深度的变化率。
实际情况下,一些类型的土(如超固结黏土)在深度方向上剪切模量变化很小,此时b=0,相当于均匀的土体。大部分正常固结的黏土剪切模量沿着深度大致线性变化,不同的土体剪切模量变化率不一样(b≠0)。本文计算了b=0、b=1、b=5共3种不同的非均匀基础(如图10所示),研究土体非均匀性对桶基的动阻抗的影响。模型其他参数:桶基厚径比t/R=0.01,长径比固定为L/R=2,Ef=210 GPa,土体参考点处G0=50 MPa,ρs=1 800 kg/m3,νs=0.33。
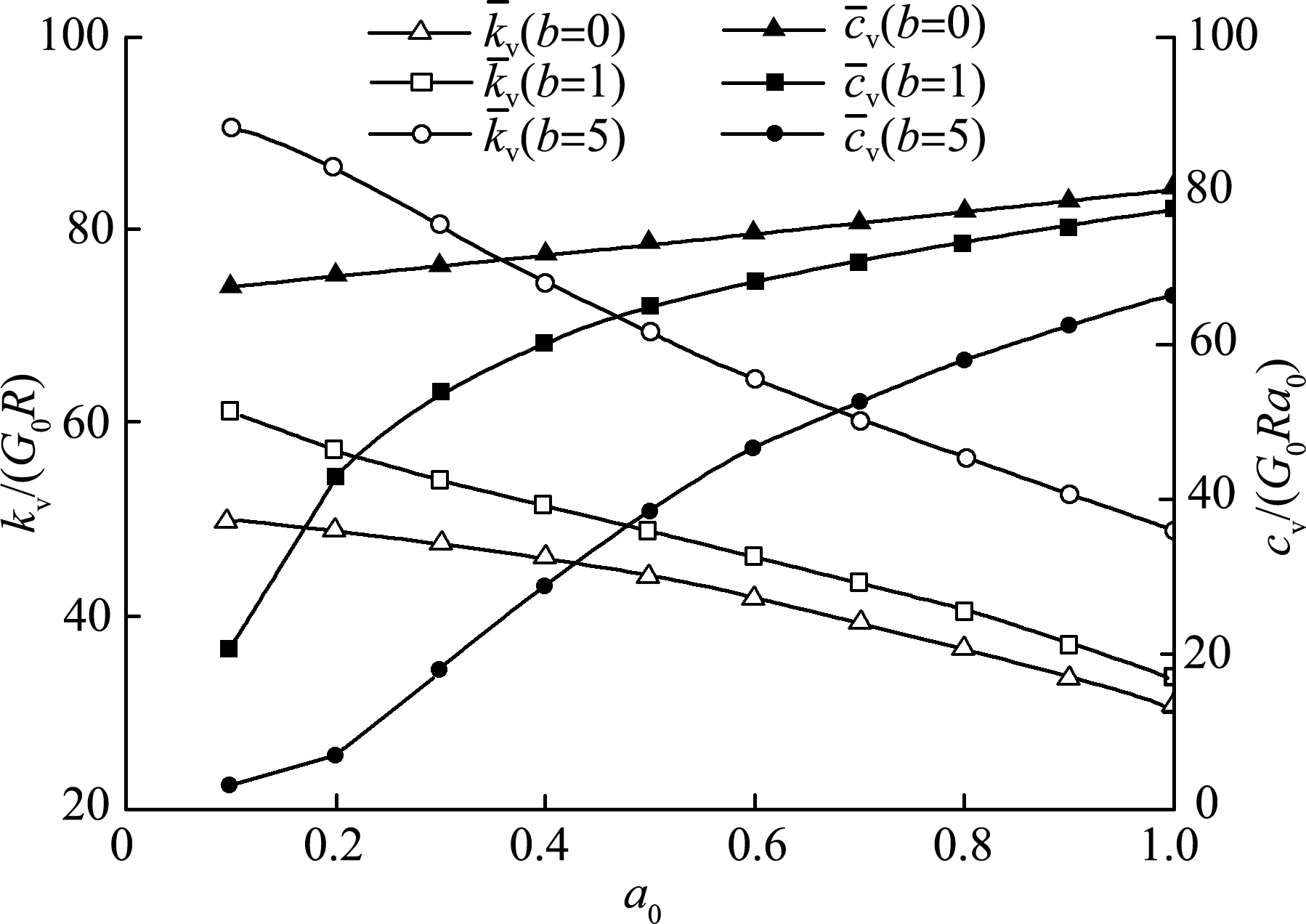
图11 非均匀土体下桶基竖向初始动阻抗Fig.11 Vertical initial dynamic impedance of bucket foundation embedded in nonhomogeneous soil


4 结 论

b.在研究竖向初始动阻抗时,桶基可以简化为壳基础进行模拟。
c.桶基动刚度和动阻尼随着桶基厚径比、泊松比增大而变大。
d.当长径比较小时,无论用钢桶基还是混凝土桶基,都将得到相近的动力响应。
e.土体剪切模量的增大使得桶基-土体相对刚度减小。剪切模量增大,在频率较低的范围内,桶基动刚度和动阻尼均变小。同时,土体的非均匀性变大,产生影响类似于土体剪切模量增大,土体不均匀系数越大,动刚度和动阻尼越小。非均匀性变大,动阻尼对无量纲频率变得更敏感,动阻尼在低频时迅速减小并趋于零。
[1] SENDERS M. Tripods with suction caissons as foundations for offshore wind turbines on sand[C]//Taylor and Francis Group. International Symposium on Frontiers on Offshore Geotechnics (ISFOG 2005). London: Taylor and Francis Group, 2005: 397-410.
[2] VERSTEIJLEN W G, VAN DALEN K N, METRIKINE A V, et al. Assessing the small-strain soil stiffness for offshore wind turbines based on in situ seismic measurements[J]. Journal of Physics (Conference Series), 2014, 524(1):12-88.
[3] BHATTACHARYA S, NIKITAS N, GARNSEY J, et al. Observed dynamic soil-structure interaction in scale testing of offshore wind turbine foundations[J]. Soil Dynamics and Earthquake Engineering, 2013, 54(11):47-60.
[4] HOULSBY G T, KELLY R B, HUXTABLE J, et al. Field trials of suction caissons in clay for offshore wind turbine foundations[J]. Géotechnique, 2005, 55(4): 287-296.
[5] HOULSBY G T, KELLY R B, HUXTABLE J, et al. Field trials of suction caissons in sand for offshore wind turbine foundations[J]. Géotechnique, 2006, 56(1): 3-10.
[6] LIINGAARD M, ANDERSEN L, IBSEN L B. Impedance of flexible suction caissons [J]. Earthquake Engineering and Structural Dynamics, 2007, 36(14): 2249-2271.
[7] LIINGAARD M. Dynamic behaviour of suction caissons [D]. Aalborg :Aalborg University, 2006.
[8] 贺瑞. 海底基础动力特性研究[D]. 杭州:浙江大学, 2014.
[9] 武科. 滩海吸力式桶形基础承载力特性研究[D]. 大连:大连理工大学, 2007.
[10] KUHLEMEYER R L, LYSMER J. Finite element method accuracy for wave propagation problems[J]. Journal of Soil Mechanics and Foundations Div, 1973, 99(5):421-427.
[11] LYSMER J, UDAKA T, TSAI C F, et al.FLUSH-A computer program for approximate 3-D analysis of soil-structure interaction problems[R]. Berkeley: Earthquake Engineering Research Center, 1975.
[12] LYSMER J. Finitedynamic model for infinite media[J]. Journal of the Engineering Mechanics Division, 1969, 95(4):859-878.
[13] LYNN P P, HADID H A. Infinite elements with 1/rn type decay[J]. International Journal for Numerical Methods in Engineering, 1981, 17(3): 347-355.
[14] BORJA R I, WU W H, SMITH H A. Nonlinear response of vertically oscillating rigid foundations[J]. Journal of Geotechnical Engineering, 1993, 119(5): 893-911.
[15] LUCO J E, WESTMANN R A. Dynamicresponse of circular footings[J]. Journal of the Engineering Mechanics Division, 1971, 97:1381-1395.
[16] DOHERTY J P, HOULSBY G T, DEEKS A J. Stiffness of flexible caisson foundations embedded in nonhomogeneous elastic soil [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2005, 131(12): 1498-1508.
[17] DOHERTY J P, DEEKS A J. Elastic response of circular footings embedded in a non-homogeneous half-space[J]. Géotechnique, 2003, 53(8): 703-714.
[18] GIBSON R E. Some results concerning displacements and stresses in a non-homogeneous elastic half-space[J]. Géotechnique, 1967, 17(1): 58-67.
Analysis of factors influencing vertical initial dynamic impedance of bucket foundations for offshore wind turbine
LIN Jie1,2, HE Rui1,2, ZHENG Jinhai1,2
(1.CollegeofHarbor,CoastalandOffshoreEngineering,HohaiUniversity,Nanjing210098,China;2.KeyLaboratoryofCoastalDisasterandDefence,MinistryofEducation,HohaiUniversity,Nanjing210098,China)
A finite element model of bucket foundation embedded in an elastic half-space was established using the finite element software ABAQUS. The accuracy of simulated results of the model was verified by comparing the numerical solution with existing analytical solutions. The influences of different factors on the vertical initial dynamic impedance of bucket foundation and the relationship between initial dynamic impedances of the bucket foundation and shell foundation were studied. The results show that the length-to-diameter ratio and thickness-to-diameter ratio of the bucket foundation, soil Poisson’s ratio, soil shear modulus, and soil nonhomogeneity have significant influence on the initial impedance, while bucket foundation material has little influence on the initial impedance. The initial impedances of the bucket foundation and shell foundation are nearly the same, and the bucket foundation can be simplified as the shell foundation in simulated calculation.
offshore wind turbine; bucket foundation; vertical initial dynamic impedance; finite element method
10.3876/j.issn.1000-1980.2017.03.012
2016-08-26
国家自然科学基金青年基金(51509082);江苏省自然科学基金(BK20150804)
林捷(1991—),男,江苏南京人,硕士研究生,主要从事工程结构物及其与周围介质的相互作用研究。E-mail:phlinjie@163.com
贺瑞,讲师。E-mail:herui0827@163.com
TU476
A
1000-1980(2017)03-0263-08
