拉剪倾倒型危岩失稳影响因素研究
2017-06-13吴礼舟吴华登
何 强,吴礼舟,李 部,吴华登
(成都理工大学地质灾害防治与地质环境保护国家重点实验室,四川 成都 610059)
拉剪倾倒型危岩失稳影响因素研究
何 强,吴礼舟,李 部,吴华登
(成都理工大学地质灾害防治与地质环境保护国家重点实验室,四川 成都 610059)
运用断裂力学分析危岩中的倾倒变形破坏,基于岩石拉剪断裂试验,研究裂纹在载荷作用下起裂、扩展规律,探索断裂过程中裂纹的扩展行为,并探讨裂纹长度、宽度、倾角与荷载位置对危岩失稳模式与稳定性的影响。以重庆万州太白岩危岩为例,利用有限元软件ANSYS计算不同裂纹条件下裂纹尖端的应力状态,并讨论其与联合断裂应力强度因子的关系,模拟裂纹扩展的动态过程。结果表明,拉剪倾倒型危岩在受力破坏过程中,裂纹尖端出现拉应力集中,危岩的开裂从张拉破坏开始,下部出现压剪破坏,危岩稳定性的影响因子敏感性从大到小依次为:荷载位置、裂纹长度、裂纹倾角、裂纹宽度。
危岩;主控结构面;拉剪断裂试验;数值计算;裂纹扩展;重庆万州太白岩
危岩是我国主要地质灾害之一,从危岩失稳的力学机制出发,将其分为坠落式危岩、倾倒式危岩和滑塌式危岩[1]。其中倾倒式危岩在我国西南地区及三峡地区分布广泛,具有数量多、稳定性差、致灾严重等特性[2]。
目前,国内外众学者对危岩失稳模式开展了研究。孙云志等[3]和谢全敏等[4]运用赤平极射投影及模糊数学建立了定性及半定量的危岩稳定性计算方法;刘卫华等[5]使用改进的静力平衡定量分析方法对危岩稳定性进行定量评价;Braathen等[6]引入损伤力学,将危岩失稳破坏的根本原因归结为主控结构面的损伤断裂过程;陈洪凯等[7-8]对倾倒式危岩力学机理建立了比较系统的理论;李佳壕等[9]利用解析法和数值计算研究了危岩的应力强度因子;刘卫华等[10]对高边坡危岩体进行分类并提出了一种稳定性分析与评价的方法。
由于危岩研究难度较大,基于试验尺度下的危岩稳定性研究难以得到突破。危岩尺寸大小和主控结构面几何参数均对危岩失稳存在一定的影响,特别是针对不同边界条件与荷载条件的危岩体,一般的解析方法分析其断裂行为难以得到应用和推广。试验模拟和数值方法则有效弥补了解析上受限于形状等因素的制约。对于以拉剪复合裂纹为主的倾倒式危岩,影响其失稳破坏的内因主要与自身重力和裂纹的贯通程度有关,外因则主要考虑外部荷载的作用,目前还缺少通过模型试验和数值分析的方法来实现对这些影响因子的具体研究,且由于此类危岩体的受力形式多种多样,仅采用现有的方法去判断不尽合理。
本文基于断裂力学原理,通过岩石断裂试验研究拉剪倾倒型危岩在单轴荷载作用下的裂隙扩展、贯通的规律,讨论裂纹参数与荷载位置对危岩稳定性的影响,利用ANSYS软件分析不同裂纹参数条件下裂纹尖端的应力状态,研究裂纹扩展的动态过程。
1 Ⅰ-Ⅱ拉剪复合型裂纹起裂分析
1.1 Ⅰ-Ⅱ复合型裂纹尖端应力-应变
岩石材料在外荷载作用下的断裂机理比较复杂,一般表现为:裂纹的萌生与启裂、扩展、贯通直至完全破坏,从其断裂形式上可以分为张开型(I型)、滑移型(II型)、撕裂型(III型)及其复合型断裂。当裂纹尖端同时受到Ⅰ型和Ⅱ型应力场的作用时,裂纹发生Ⅰ-Ⅱ复合型断裂,裂纹将与原裂纹方向呈一定角度发生扩展,且失稳条件更复杂。根据Ⅰ-Ⅱ复合型裂纹的受力形式,其裂纹尖端在极坐标中的应力分量由式(1)表达[11]:
(1)
其中
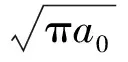
式中:σrr——裂纹尖端的径向应力;σθθ——裂纹尖端的周向拉应力;τrθ——裂纹尖端的剪切应力;a0——裂纹半长;KⅠ、KⅡ——原裂纹面上Ⅰ、Ⅱ型应力强度因子;θ——裂纹偏离的角度(逆时针为正,顺时针为负);r——距离裂纹尖端的距离。
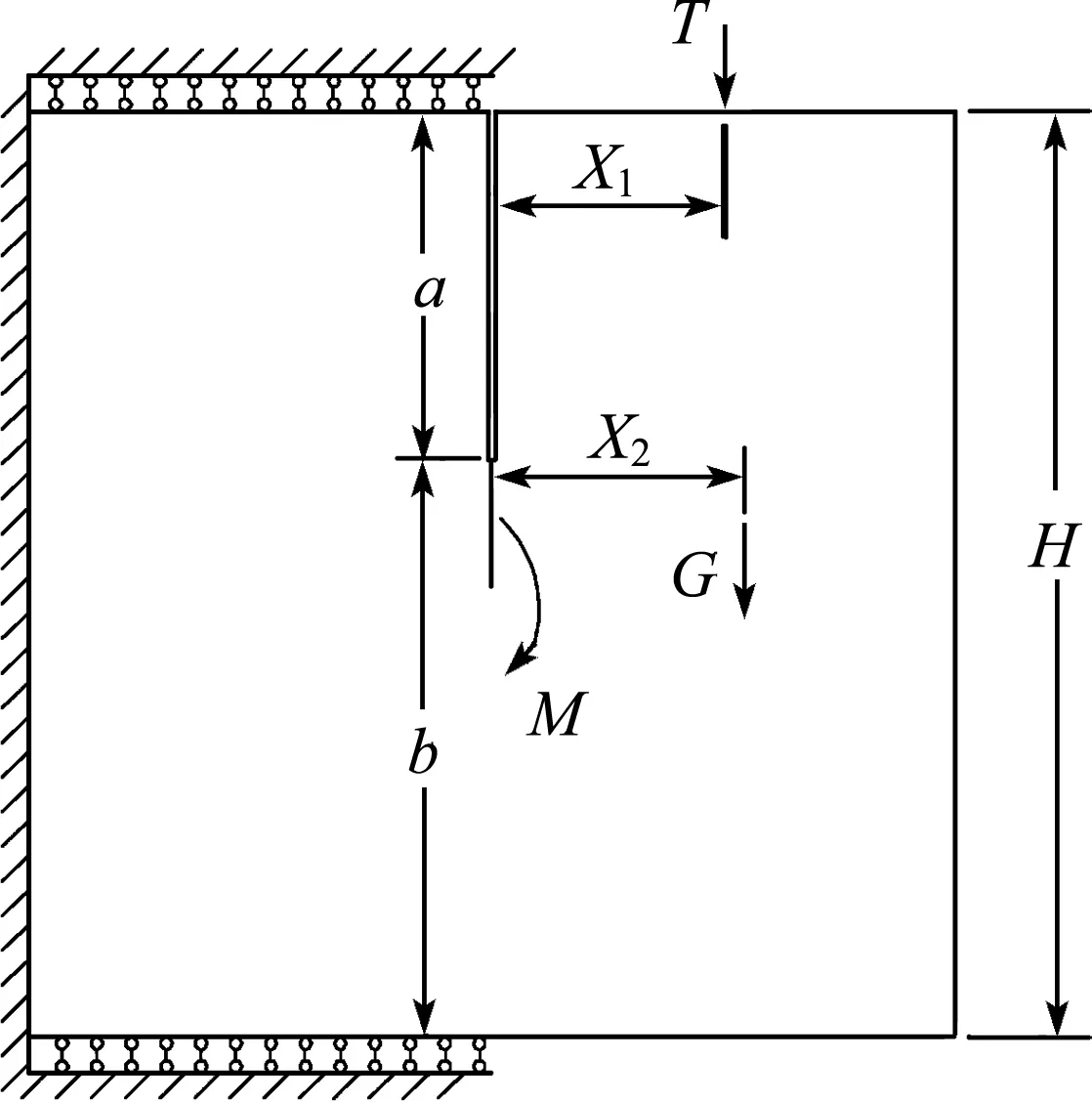
图1 危岩力学模型Fig.1 Mechanical model of unstable rock
1.2 拉剪复合型裂纹断裂分析
在实际调查中,拉剪倾倒型危岩主控结构面倾角变化较大,一般多大于25°,多为陡崖或陡坡的卸荷张拉结构面,且主控结构面下段部潜存与陡崖或陡坡岩体内。危岩体重心位于主控结构面外侧是此类危岩的关键,在荷载作用下通常围绕主控结构面的下端部或下端部与临空面的交点旋转倾倒破坏,危岩体呈现拉剪破坏。对于危岩主控结构面断裂模型,前人已经做了大量的研究[12]。但在实际危岩体中,复杂的边界条件以及荷载情况往往导致危岩不同类型的破坏。笔者针对此类危岩体提出其受力形式下的力学模型,危岩力学模型如图1所示(图中H为模型高度,T为施加的外荷载,a和b为主控结构面长度,G为重力),该危岩力学模型主要适用于危岩主控结构面一侧受力的危岩破坏情况。
针对本文拉剪倾倒型危岩的受力形式,可以将其分解为纯剪切和纯弯矩2种断裂模型。纯剪切断裂主控结构面受到一对剪切力的作用,裂纹将沿着最大剪应力方向扩展,等效于Ⅱ型断裂;纯弯矩断裂主控结构面受到一对弯矩的作用,裂纹将沿着裂纹尖端扩展,等效于Ⅰ型断裂。
根据应力强度因子手册[13],在主控结构面承受剪切应力作用下,裂纹尖端产生的应力强度因子为
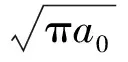
(2)
在主控结构面上作用单位厚度的弯矩M,裂纹尖端产生的应力强度因子为
(3)
在拉剪复合型断裂中,主控结构面的扩展方向不一定在主控结构面的延伸线上,因此采用最大周向拉应力理论来研究危岩主控结构面的应力强度因子和断裂角。Ⅰ-Ⅱ型复合裂纹沿着最大拉应力σmax所对应的方向θ0扩展,该方向需满足[14]:

(4)
求式(4)得
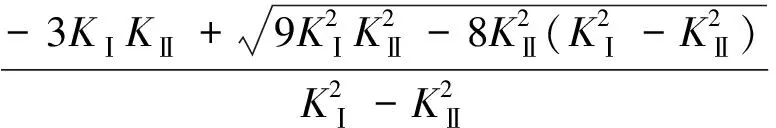
(5)
对应于最大周向拉应力的应力强度因子为

(6)
当Ke≥KⅠC(岩石断裂韧度)时,危岩主控结构面发生断裂扩展。
2 拉剪断裂试验
2.1 试验概况
试验试样采用四川南江的杂砂岩,该岩样颗粒较细,结构较为致密,满足脆性断裂的特点。将砂岩制成80 mm×80 mm×80 mm的立方体(误差大小在1%以内),为确保试验中荷载的均匀度,岩样面必须平整,岩样的裂隙加工在铣床上完成。
试验共设计5组,每组3个岩样,主要分析裂纹长度、宽度、倾角和荷载位置以及试样尺寸大小的影响,在尺寸大小和荷载位置相同的情况下裂纹长度、宽度与倾角情况如表1所示。
由于实际危岩体中外荷载的分布不均,因此在本试验中设置不同的荷载位置,分别为距裂纹10 mm、20 mm、30 mm。
2.2 试验过程
试验在MTS试验机上进行,并借助辅助模具固定岩样裂纹一侧,在裂纹另一侧施加线性荷载(图2),试验过程中采用位移控制方式,其速率为0.1 mm/min,并由位移传感器测量裂纹法向位移。
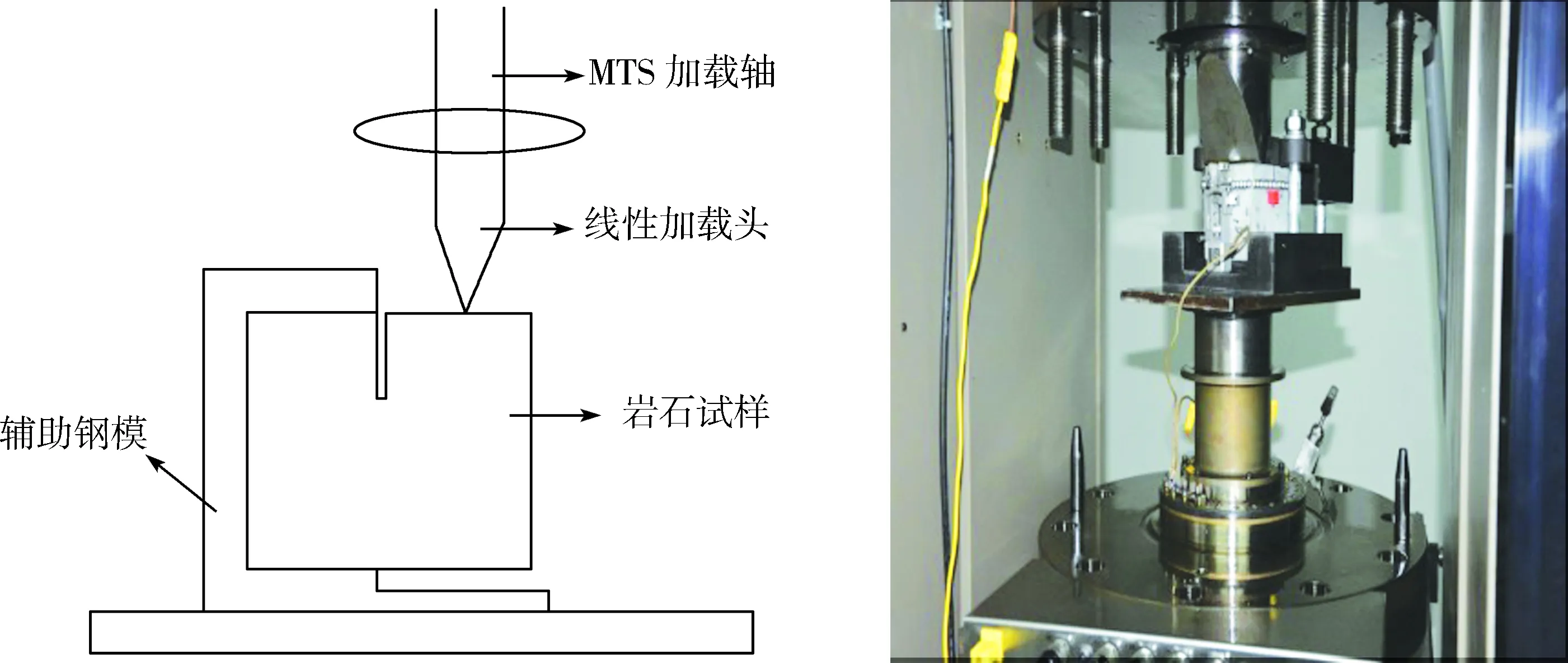
(a) 剖面图 (b)试验机照片图2 试验装置示意图Fig.2 Sketch map of tests
2.3 试验结果
图3为不同裂纹长度岩样全过程位移-荷载曲线。由图3可知,岩样均是由初始荷载达到峰值强度,然后进入迅速卸荷过程,随着裂纹长度的增加,峰值强度逐渐减小,从约14 kN减小到约5 kN,同时切向位移也逐渐减小(图3(a));裂纹面的法向位移随着裂纹长度的增加而增大(图3(b)),最大位移量约为0.12 mm,由于相同弯矩作用下的岩样,裂纹越长,破坏需要的时间越短,产生的法向位移越小。
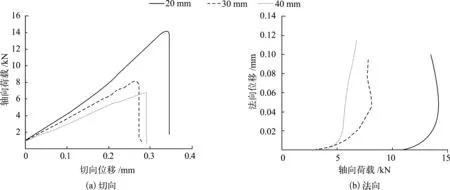
图3 不同裂纹长度岩样全过程位移-荷载曲线Fig.3 Complete displacement-load curves of rock samples with different crack lengths
根据不同荷载位置的试验结果可知:荷载位置越靠近裂纹,峰值强度越大,裂纹面切向位移也越大,最大峰值强度可达15 kN;裂纹面的法向位移随荷载位置与裂纹距离的增大而增大,且起始破裂时间较短,这是由于荷载位置离裂纹越远,裂纹所受的剪应力越小,弯矩作用越强,张拉破坏作用越强,裂纹面法向位移越大。
裂纹角度对试验结果的影响表明,90°时裂纹倾角的岩样峰值强度最大,随着倾角的递减,峰值强度呈递减趋势。在裂纹倾角小于90°时,由于裂纹先经历了压剪过程,使裂纹闭合。而当偏离角度越大时,裂纹受到的初始剪切破坏作用越强,张拉破坏作用越弱,裂纹的法向位移随着裂纹倾角的增大而增大。
从上述试验结果可知,影响危岩稳定性的因素由强到弱依次为:荷载位置、裂纹长度、裂纹倾角、裂纹宽度。
3 算例与数值计算

图4 危岩几何模型Fig.4 Geometric model of unstable rock
由于工程岩体所受荷载条件以及边界条件不同,一般的解析法不能分析主控结构面的应力特征及其断裂扩展行为,而数值法比较常用。以重庆万州太白岩南坡W25号危岩体为数值计算的物理模型[2],将危岩主控结构面类比为宏观裂纹,并对危岩体的边界条件进行定义,研究重力作用下危岩体在不同裂纹参数下裂纹尖端的应力状态以及与联合断裂应力强度因子的关系,几何尺寸如图4所示。
重庆万州太白岩南坡W25号危岩主控结构面发育单一,平均倾角β=87°,深度h=8.6 m,危岩体高度H=13.5 m。该危岩属于倾倒式危岩,由长石石英砂岩构成。主要物理力学参数为:弹性模量E=8 300 MPa,泊松比μ=0.16,抗拉强度σt=500 kPa。在ANSYS中建立几何模型后,网格划分的单元类型取8节点平面应力单元,网格数量为1 692。约束条件为裂纹左侧上下边界(AB、GE)竖向位移为0,左边界AG横向位移为0,重力加速度g取9.8 m/s2。
3.1 不同裂纹尺寸下的危岩应力分布
从图5可以看到,在裂纹尖端与临空端点附近同时出现应力集中,最大主应力出现在裂纹尖端,处于受拉状态,a/H=0.44时最大主应力约为4.85 MPa,a/H=0.64时最大主应力约为5.51 MPa。临空端点处于受压状态,且裂纹越长,最大主应力越大,应力集中范围越大,危岩越不稳定。
图6显示了不同裂纹宽度下的最大主应力。b/H=0.001 25时,最大主应力为4.85 MPa,b/H=0.002 59时最大主应力为4.39 MPa。可见裂纹宽度的增加使危岩的应力集中范围增大,但拉应力与压应力值均有所

(a) a/H=0.44

(b) a/H=0.64
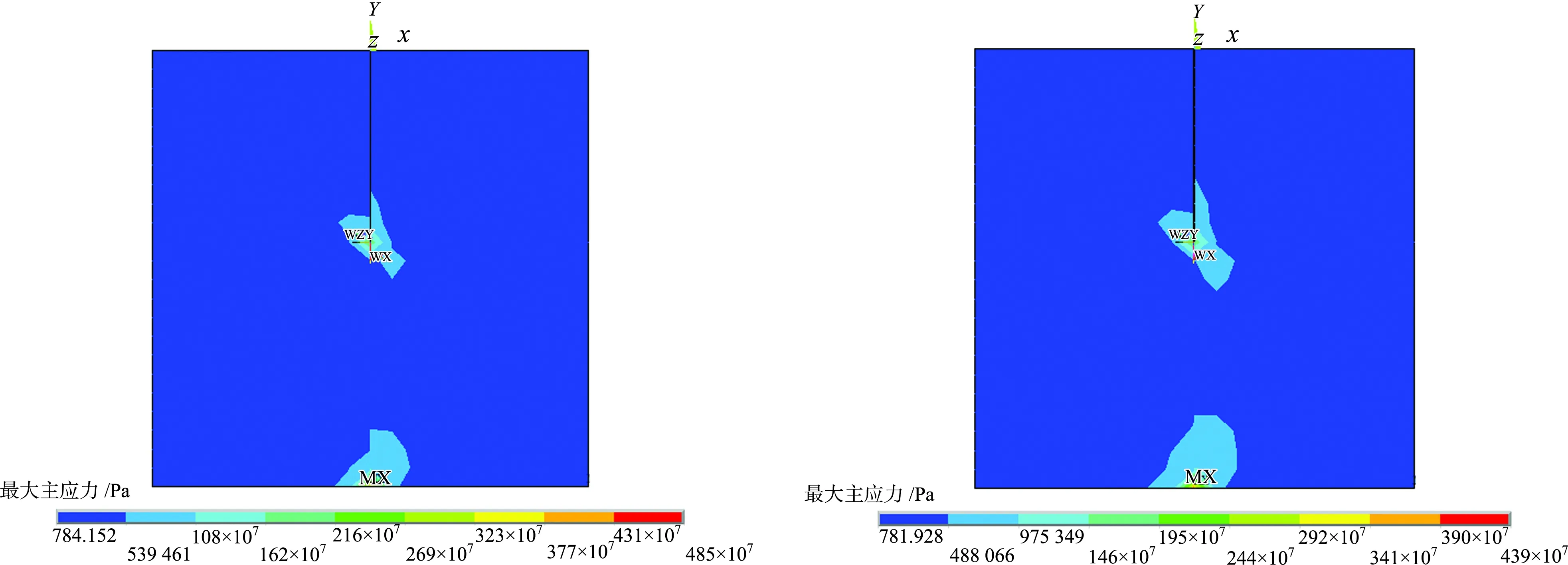
(a) b/H=0.001 25 (b) b/H=0.002 59图6 不同裂纹宽度时最大主应力Fig.6 Maximum principal stresses for different crack widths
减小,因此,危岩裂纹宽度对危岩稳定性影响较小。
图7为不同裂纹倾角的最大主应力图。β=90°时最大主应力为4.85 MPa,β=70°时最大主应力为1.76 MPa。最大主应力在裂纹尖端与临空端点同时出现,且随着倾角的减小,危岩顶部主控结构面左侧也出现应力集中,但最大拉应力与压应力值均减小,危岩稳定性提高。

(a) β=90° (b) β=70°图7 不同裂纹倾角时最大主应力Fig.7 Maximum principal stresses for different crack inclination angles
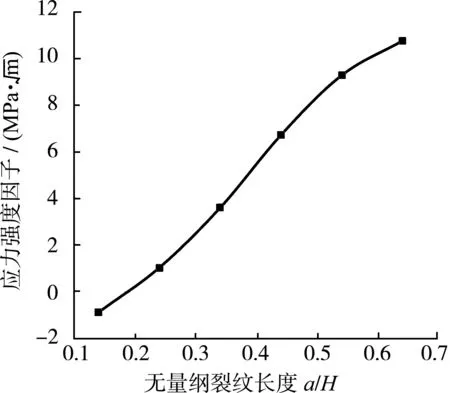
图8 联合断裂应力强度因子随无量纲裂纹长度的变化曲线Fig.8 Complex breaking stress intensity factor against dimensionless crack length
3.2 不同裂纹尺寸对应力强度因子的影响
在断裂分析中,常用的计算应力强度因子方法有位移外推法、J积分法等,本文基于相互作用积分法[15]计算模型的应力强度因子,该方法类似于J积分法,利用围线积分原理求解复合型裂纹尖端应力强度因子。对于拉剪复合型断裂KⅠ>0,并且随着裂纹长度的增加而增大,而由于KⅡ的正负性未知,联合断裂应力强度因子的正负性则很难判断。图8为联合断裂应力强度因子随无量纲裂纹长度的变化曲线,联合断裂应力强度因子随无量纲裂纹长度的增大而增大。在无量纲裂纹长度较小时,联合断裂应力强度因子为负值,而根据陈洪凯提出的联合断裂应力强度因子Ke与Ⅰ型、Ⅱ型应力强度因子的关系(式(7)),说明此时岩体的Ⅱ型应力强度因子为正值,但其与Ⅰ型应力强度因子值的大小无法判断。

(7)
计算结果表明,联合断裂应力强度因子随裂纹倾角的增大呈现先减小后增大的趋势,倾角在约60°时,其值最小;而联合断裂应力强度因子随裂纹宽度的改变几乎没有变化,其值比较稳定。
从上述分析结果可知,裂纹长度的改变对裂纹尖端应力强度因子的影响最大,裂纹倾角次之,而裂纹宽度的改变对裂纹尖端应力强度因子几乎没有影响,从而可以得出数值计算结果中影响危岩失稳的影响因子敏感性由大到小依次为:裂纹长度、裂纹倾角、裂纹宽度,这与试验结果一致。
3.3 裂纹扩展模拟
在ANSYS大型有限元软件中,利用虚拟裂纹闭合法[16]实现了裂纹扩展模拟。该方法的原理是通过计算裂纹体的能量释放率而进行裂纹扩展计算,主要分析步骤为:(a)建立预先定义路径的有限元模型;(b)进行能量释放率计算;(c)进行裂纹扩展模拟。在裂纹扩展模拟中,最难的是网格的划分,而该方法网格的独立性使得模拟过程相对简单。
计算模型采用试验模型,模型边界条件及材料参数与W25号危岩体一致,取裂纹长度为30 mm,裂纹倾角为90°,裂纹宽度为1 mm,网格划分采用4节点单元,定义为平面应力,由于裂隙的建立与网格是完全独立的,因此无须再对裂尖单元做加密处理,也无须采用三角形单元节点消除奇异性。
图9为裂纹扩展模拟结果。模型裂纹开始以约35°起裂。图9(a)为模型起裂时裂纹尖端应力集中,然后逐步向临空部位扩展。随着裂隙的不断扩展,模型体整体重心向外侧移动,加速了裂隙扩展速度,裂隙迅速贯通,模型体破坏。图9(b)为模型体裂纹扩展轨迹。

(a)起裂 (b)裂纹扩展轨迹图9 荷载作用下的裂纹扩展结果Fig.9 Crack propagation under loading
图10为不同裂纹长度岩样的试验结果。对比数值计算与试验结果(图9与图10),二者的裂纹扩展路径基本一致,均是沿裂纹尖端以一角度起裂,由于下部临空且剪应力较大,随后裂纹扩展轨迹逐渐平缓,直至贯通到底部临空端点处。

(a) a/H=0.25 (b) a/H=0.375图10 不同裂纹长度岩样破坏形态Fig.10 Failure modes of rock samples for different crack lengths
4 结 论
a.主控结构面参数及荷载情况是影响拉剪倾倒型危岩失稳的主要因素,其影响因子敏感性由大到小依次为:荷载位置、裂纹长度、裂纹倾角、裂纹宽度。
b.拉剪倾倒型危岩在受力破坏过程中,裂纹尖端出现拉应力集中,而危岩的开裂从张拉破坏开始,下部出现压剪破坏。
c.非对称受力的拉剪倾倒型危岩主控结构面在断裂破坏过程中,裂纹以某一角度起始于裂纹尖端,逐步向临空部位扩展,最后回到临空位置底部贯通,裂纹面扩展的切向位移大于其法向位移。
d.通过模型试验和数值计算方法研究裂纹起裂扩展的机理,二者得到的结果一致,验证了模型失稳破坏结果的合理性。
[1] 陈洪凯, 唐红梅, 王蓉. 三峡库区危岩稳定性计算方法及应用[J]. 岩石力学与工程学报,2004,23(4):614-619. (CHEN Hongkai, TANG Hongmei, WANG Rong. Calculation method of stability for unstable rock and application to the three Gorges Reservoir[J]. Rock Mechanics and Engineering, 2004,23(4): 614-619.(in Chinese))
[2] 唐红梅, 叶四桥, 陈洪凯. 危岩主控结构面损伤-断裂数值模拟研究[J]. 重庆交通学院学报,2005,24(4):84-87. (TANG Hongmei, YE Siqiao, CHEN Hongkai. Research on numerical simulation of damage-fracture process of control fissure in unstable rock[J]. Journal of Chongqing Jiaotong University, 2005, 24(4): 84-87. (in Chinese))
[3] 孙云志, 任自民, 王立,等. 奉节李子垭危岩体稳定性研究[J]. 人民长江,1994(9):48-53. (SUN Yunzhi, REN Zimin, WANG Li, et al. The Fengjie plums dangerous rock mass stability studies[J]. Yangtze magazine, 1994(9): 48-53. (in Chinese))
[4] 谢全敏, 夏元友. 危岩块体稳定性的综合评价方法分析[J]. 岩土力学,2002,23(6):775-777,781. (XIE Quanmin, XIA Yuanyou. Comprehensive assessment method of stability of critical rock-block mass and its application[J]. Rock and Soil Mechanics, 2002, 23(6): 775-777, 781. (in Chinese))
[5] 刘卫华, 黄润秋. 危岩稳定性定量评价研究[J]. 路基工程,2014(6):51-57. (LIU Weihua, HUANG Runqiu. Study on quantitative evaluation of perilous rock stability[J]. Subgrade, 2014(6): 51-57. (in Chinese))
[6] BRAATHEN A, BLIKRA L H, BERG S, et al. Rock-slope failure in norway: type, geometry, deformation mechanisms and stability [J]. Norweigian Journal of Geology, 2004, 84(1): 67-88.
[7] 陈洪凯, 唐红梅. 危岩主控结构面强度参数计算方法[J]. 工程地质学报,2008,16(1):37-41. (CHEN Hongkai, TANG Hongme. Method for calculating strength parameters of structural planes controlling the rock block stability[J].Journal of Engineering Geology, 2008, 16(1): 37-41. (in Chinese))
[8] 陈洪凯, 鲜学福, 唐红梅. 危岩稳定性断裂力学计算方法[J]. 重庆大学学报,2009,32(4):434-437,452. (CHEN Hongkai, XIAN Xuefu, TANG Hongmei. Stability analysis method for perilous rock by fracture mechanics[J].Journal of Chongqing University, 2009, 32(4): 434-437, 452. (in Chinese))
[9] 李佳壕, 吴礼舟. 危岩应力强度因子的计算研究[J]. 工程地质学报,2013,21(2):236-242. (LI Jiahao, WU Lizhou. Calculation of stress intensity factor of unstable rock[J]. Journal of Engineering Geology, 2013, 21(2): 236-242. (in Chinese))
[10] 刘卫华, 罗倩, 黄润秋,等. 溪洛渡水电工程坝区高边坡危岩体分类及稳定性评价[J].水利水电科技进展,2008,28(4):48-51.(LIU Weihua, LUO Qian, HUANG Runqiu, et al. Quality classification and stability evaluation of unstable rock mass on high rock slope of Xiluodu Hydropower Project[J]. Advances in Science and Technology of Water resources, 2008, 28(4): 48-51. (in Chinese))
[11] 李世愚, 和泰名. 岩石断裂力学导论[M]. 北京:中国科学技术大学出版社,2010.
[12] CHEN H K, TANG H M, YE S Q. Research on damage model of control fissure in perilous rock [J]. Applied Mathematics and Mechanics, 2006, 27(7):967-974. (in Chinese))
[13] 中国航空研究院.应力强度因子手册[M]. 北京:科学出版社,1993.
[14] 陈洪凯, 胡明, 唐红梅. 危岩锚固机理的断裂力学分析[J]. 重庆建筑大学学报,2006,28(5):101-105. (CHEN Hongkai, HU Ming, TANG Hongmei. Fracture mechanics analysis of control fissure of bolted perilous rock[J]. Journal of Chongqing Jianzhu University, 2006, 28(5): 101-105. (in Chinese))
[15] 宫经全, 张少钦. 基于相互作用积分法的应力强度因子计算[J]. 南昌航空大学学报(自然科学版) ,2015,29(1):42-48. (GONG Jingquan, ZHANG shaoqin. Computation of the stress intensity factor based on the interaction integral method[J]. Journal of Nanchang Aeronautical University (Natural Science), 2015, 29(1): 42-48. (in Chinese))
[16] 肖涛, 左正兴. 虚拟裂纹闭合法在结构断裂分析中的应用[J]. 计算力学学报,2008(增刊1):16-19. (XIAO Tao, ZUO Zhengxing. Application of virtual crack closure technique in structure fracture analysis[J]. Journal of Computational Mechanics, 2008(Sup1): 16-19. (in Chinese))
Factors of instability of toppling unstable rocks subjected to tensile and shear stresses
HE Qiang, WU Lizhou, LI Bu, WU Huadeng
(StateKeyLaboratoryofGeohazardPreventionandGeoenvironmentProtection,ChengduUniversityofTechnology,Chengdu610059,China)
Toppling failure of unstable rocks was analyzed using fracture mechanics. Based on tensile-shear fracture tests of rock samples, fracture initiation and propagation mechanisms under loading were analyzed, and crack propagation during the fracture process was investigated. The effects of the crack length, width, and inclination angle as well as the loading point on the failure mode and stability of unstable rocks were discussed. An overhanging rock, the Taibaiyan unstable rock in Wanzhou District of Chongqing City was used as a case study. The stress state of crack tips under different cracking conditions was calculated using the finite element software ANSYS, the relationship between the complex breaking stress intensity factor and stress state was discussed, and the dynamic process of crack propagation was simulated. Results show that, during the processes of tension, shear, and toppling failures of unstable rocks, tensile stresses were concentrated at creak tips, unstable rock cracking was first induced by tension failures, and shear-compression failures occurred at the bottom. The sensibilities of the factors to the instability of unstable rocks were ranked in an descending order as follows: the loading position, crack length, crack inclination angle, and crack width.
unstable rock; main structural plane; tensile-shear fracture test; numerical calculation; crack propagation; Taibaiyan in Wanzhou District of Chongqing City
10.3876/j.issn.1000-1980.2017.03.008
2016-08-28
国家重点基础研究计划(973计划)(2013CB733202);国家自然科学基金重点项目(41130745);四川省青年科技创新研究团队基金(2015TD0030)
何强(1990—),男,四川遂宁人,硕士研究生,主要从事岩土体稳定性研究。E-mail: 398817053@qq.com
吴礼舟,教授。E-mail:wulizhou07@cdut.cn
P642
A
1000-1980(2017)03-0235-08
