并排水平轴潮流能水轮机组水动力特性研究
2017-06-13张继生曹运修吴修广
张继生,曹运修,吴修广,宋 凡,戴 鹏
(1.河海大学港口海岸与近海工程学院,江苏 南京 210098;2.浙江省水利河口研究院,浙江 杭州 310020)
并排水平轴潮流能水轮机组水动力特性研究
张继生1,曹运修1,吴修广2,宋 凡1,戴 鹏1
(1.河海大学港口海岸与近海工程学院,江苏 南京 210098;2.浙江省水利河口研究院,浙江 杭州 310020)
基于FLOW-3D软件平台建立三维水动力计算模型,研究水轮机横向间距、相对安装高度和来流速度对二台并排布置的水平轴潮流能水轮机组的水动力特性的影响。结果表明:随着横向间距的增大,水轮机组受到的与来流方向相同的最大水流作用力有一定减小,最大降幅达6.62%,尾流场中水流加速区域的最大流速也略有减小,最大降幅约1.21%;水轮机组相对安装高度和来流速度的改变,对其飞逸转速、最大水流作用力以及尾流场有显著影响。
潮流能;水轮机;横向间距;相对安装高度;来流速度;水动力特性;数值模拟
为了减缓能源紧张局势和改善环境污染现状,迫切需要开发清洁可再生能源[1],而潮流能凭借其对环境影响小、可预测性强及能量巨大等优点受到广泛关注[2]。潮流能发电装置目前发展最成熟的是水平轴潮流能水轮机[3-4]。水轮机周边的流场复杂,对水轮机的发电性能和布局方式影响很大[5],研究潮流能水轮机周边的水动力特性可以为科学地开发潮流能资源提供依据[6]。
近年来,潮流能水轮机(组)水动力特性得到不少关注和研究。在单台水轮机方面,Li等[7]研究了坐底式水平轴潮流能水轮机周边的流场特性,发现水轮机和单桩的组合形式会显著改变结构周边的水流运动,水轮机后方出现了大范围的尾流区。水轮机安装高度的增加会导致转速增加,降低水体的总作用力;来流速度增加,水轮机的飞逸转速和动能会明显增加。McAdam等[8-10]进行了大量的水槽模型试验,研究水深和流速对水轮机叶片的流体荷载、自由水位变化等的影响,总结各参数的影响规律。张亚超等[11]通过物理模型试验研究不同初始流速和推力系数下单台水平轴潮流能水轮机的尾流效应。在多台水轮机方面,辛小鹏等[12]研究了双转子水轮机前后布置时的水动力特性,总结转子间距对水轮机性能的影响规律。Mycek等[13]重点研究了2台前后布置的水平轴潮流能水轮机的相互作用,测量了水轮机间的纵向间距对第二台水轮机性能和尾流的影响规律,并与单台水轮机的结果进行对比,结果显示,第二台水轮机受到第一台水轮机的影响明显。Divett等[14]和Stallard等[15]研究了小型水轮机阵列的布局,发现第二排水轮机至少要在第一排水轮机下游5D处(D为水轮机叶片直径),才能让水轮机捕获更多的能量。
由此可见,尽管前人研究了单台或2台前后布置的水轮机周边的水力特性,但是对于2台并排布置的单桩支撑的水平轴潮流能水轮机组,其周边的水动力特性尚不明确。本文基于FLOW-3D软件平台建立三维水动力计算模型,研究2台三叶片水平轴潮流能水轮机并排布置形成的机组工况,分析2台水轮机的横向间距、相对安装高度(水轮机安装高度与水深的比值)和来流速度对其周边水动力特性的影响规律。
1 数 学 模 型
基于FLOW-3D软件平台建立计算模型,包含水动力模块和GMO(general moving object)模块。采用有限差分法求解N-S(Navier-Stokes)方程组,离散采用二阶单调保守迎风差分法,计算域在空间上采用矩形网格,并在水轮机区域局部加密。
1.1 水动力模块
水动力模块的控制方程是N-S方程组,基于VOF(volume of fluid)两相流方法[16]跟踪自由液面,采用LES(large eddy simulation)方法模拟计算紊动输运。质量连续方程为

(1)
式中:VF——网格单元内参与计算的流体体积所占网格大小的百分比;ρ——流体的密度;t——时间;RDIF——紊动扩散项;RSOR——质量源项;u、v、w——x、y、z方向的速度分量;Ax、Ay、Az——x、y、z方向上流体所占面积的百分比。
坐标系上3个不同方向的动量守恒方程为
(2)
(3)
(4)
式中:Gx、Gy、Gz——x、y、z方向的重力加速度;fx、fy、fz——x、y、z方向的黏性加速度;uw、vw、ww——x、y、z方向的质量源运动速度;us、vs、ws——x、y、z方向的质量源表面流体相对质量源的运动速度;δ——质量源的压力类型,在本模型中取δ=1,表示质量源为静态压力类型,这种情况下通过流量以及质量源的表面积来计算流体的速度,不需要提供压力使流体从质量源中脱离。
1.2 GMO模块
GMO模块已被广泛用来求解运动物体的流固耦合问题,其核心是FAVOR(fractional area/volume obstacle representation)方法[17],用于描述水轮机的形状、大小、所处位置和运动状态以及模拟水轮机与水流发生的相互作用。在FLOW-3D中基于FAVOR方法的理论方程如下:

(5)
式中:Sm——流体质量源项;Vf——流体所占网格的体积比;A——流体所占网格的面积比。
1.3 模型验证和应用
此模型已被成功用于研究单台单桩支撑的水平轴潮流能水轮机的水动力特性[3],本文将其用于研究2台并排布置的水平轴潮流能水轮机组的水动力特性,研究横向间距、水轮机相对安装高度和来流速度对2台并排水轮机组的水动力特性影响,为潮流能实际开发工程提供科学依据。
1.4 计算区域与网格划分
模型的数值水槽长度(沿坐标轴X方向)为180 m,宽度(沿坐标轴Y方向)为150 m,高度(沿坐标轴Z方向)为32 m,水轮机组并排布置,数值水槽和水轮机布置如图1所示。模型计算的来流速度参考SeaGen的海试工况,横向间距参考EMEC(European marine energy centre)的指导意见取2.5D,因此取2D,2.5D,3D共3个间距,安装高度参考桩基式水轮机组合(舟山潮流能示范工程)的安装水深30 m左右,为了减小水轮机转动对水面的扰动及留有一定的富余水深供某些小船只通过,因此安装高度取9 m、15 m、20 m,其相对安装高度分别为0.3、0.5、0.67。水轮机包含3个直径D=16 m的叶片,叶片厚度为0.4 m,中心轮毂直径为2.6 m,长度为3.56 m,材料密度为2 700 kg/m3,扇叶倾角(与旋转轴夹角)约为70°。为了节约计算资源,加快计算速度,模型水槽沿着长度X方向分为2个网格块,如图2所示,网格块1为包含水轮机的长48 m的区域,X方向划分95个网格,Y方向划分150个网格,Z方向划分120个网格,在水轮机处局部加密,各方向最小网格均在水轮机叶片处;网格块2为剩余的长132 m的空水槽,X方向划分140个网格,Y方向划分150个网格,Z方向划分45个网格,各方向都是均匀网格。

图1 水轮机布置示意图Fig.1 Layout of turbines

图2 网格块划分示意图Fig.2 Sketch of mesh block division
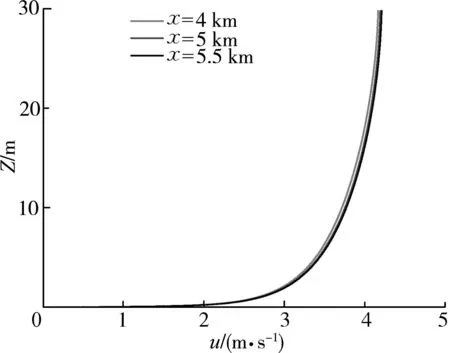
图3 数值水槽不同位置处 流速垂向分布对比Fig.3 Comparison of vertical distribution of velocity at different locations of numerical flume
1.5 初始条件和边界条件
水轮机初始旋转速度为零,初始水深为30 m,水流上方与空气接触,其表面张力取为零,底部是粗糙度为5的海床,两侧是光滑的固体边壁。模型入口采用透明网格板热启动,首先利用FLOW-3D的水动力模块建立一个长度为6 km、宽度为150 m、水深30 m的数值水槽。在数值水槽入口处给定一个实际工况中需要的流速,通过足够长时间的计算,数值水槽中水流流态稳定,流速垂向分布将趋近实际情况的垂向流速分布形态,整个水槽几个主要断面(x=4 km、x=5 km、x=5.5 km)的垂向流速分布形态如图3所示,可见沿水槽长度方向5.5 km位置以后流速垂向分布基本发展稳定。因此,在数值模型中选取水槽5.5 km位置为进口边界,并将此时的数值水槽流体参数设置为热启动文件。
2 水轮机横向间距的影响效应
通过改变2台并排布置的水平轴潮流能水轮机的横向间距,将其分别设置为2D、2.5D、3D,在不同的来流速度和相对安装高度的组合工况下,探讨横向间距对水轮机的飞逸转速、各向最大水流作用力及流场等特性的影响。为方便表达,将水轮机的飞逸转速简记为ω(单位:rad/s),将各向最大水流作用力简记为F(单位:N),将X、Y、Z方向的最大水流作用力简记为Fx、Fy、Fz。考虑叶片转动带来的不对称性,首先分析1号水轮机和2号水轮机两者的响应规律差异。以来流速度3.7 m/s、相对安装高度0.5为例予以说明,2号水轮机的ω与1号水轮机相同。2号水轮机的F和1号水轮机在量值上不完全相同(不存在对称等值关系),但差异极小且变化规律相同(表1)。例如,2号水轮机Fx随横向间距的增大而有微弱的减小,从2D到3D,降幅为2.78%,Fy受横向间距的影响很大,变化幅度达6.14%,Fz受横向间距的影响很小,变化幅度为2.85%,这些变化规律与1号水轮机是一致的。因此,下文以1号水轮机为例。

表1 来流速度为3.7 m/s时各横向间距下各向最大水流作用力
首先,研究各来流速度下横向间距对飞逸转速、各向最大水流作用力以及尾流场的影响。将相对安装高度设定为0.5,来流速度分别为2.6 m/s、3.7 m/s、4.8 m/s,横向间距分别为2D、2.5D、3D工况下,研究水轮机周边的水动力特性。
2.1 对飞逸转速的影响
在来流速度2.6 m/s条件下,在2D、2.5D、3D间距时,1号水轮机的ω分别为1.132 rad/s、1.130 rad/s、1.129 rad/s。随着水轮机横向间距的增加,ω出现微弱的减小,横向间距从2D增加到3D,水轮机ω仅减小了0.96%。在2.6 m/s来流速度下,水轮机的ω受横向间距变化的影响不显著,由于水轮机转动主要是受水流的推动作用,在同一安装高度,来流速度不变,因此水轮机的ω几乎不受横向间距的影响。同样地,来流速度为3.7 m/s和4.8 m/s的模拟结果表明,水轮机的ω受横向间距变化的影响不显著。
2.2 对各向最大水流作用力的影响
当水轮机横向间距发生变化时,水轮机叶片受到的F也会不同。当来流速度为2.6 m/s时,水轮机叶片各向受水流作用力如表2所示。水轮机Fx随着横向间距的增大而减小,降幅仅为1.48%,因为在不同的横向间距下水轮机相对安装高度是相同的,来流方向单一且流速稳定,因此受到水流的作用力相差不大;Fy在不同的横向间距下变化较大(负值表示其方向与Y轴负方向相同),各间距下的F变化率约为10%,其主要原因是横向间距不同时2台水轮机间的断面流速不一样,水体紊动强度也不一样,导致Fy相差较大;Fz变化微小,变化幅度仅2.03%,由于Z方向的水流作用力主要是浮力,而水轮机固定在海床中,受到的浮力基本一样。在来流速度为3.7 m/s和4.8 m/s的条件下,对水轮机叶片各向受力进行了研究,其变化规律与2.6 m/s流速条件下的变化规律一致。
2.3 对水轮机尾流流速剖面的影响

图4 3种横向间距在2.6 m/s来流速度下水轮机后方5D处的尾流流速剖面Fig.4 Distribution of wake flow velocity at 5D behind turbine with three lateral spacings and incoming velocity of 2.6m/s
在不同的横向间距下2台并排水轮机组尾流场变化较大,根据Stallard等[16]的研究,水轮机纵向间距至少要达到5D,因此在横向间距分别为2D、2.5D和3D情况下,研究水轮机后方5D处的尾流场情况。选取的参数是相对安装高度为0.5时,X方向流速时均值与来流速度的比值(无量纲值),简记为λ。
图4为来流速度2.6 m/s条件下水轮机后方5D处的尾流流速剖面。横向间距为2D时,2台水轮机间的加速区域宽度为25 m,λ最大值为1.237;横向间距为2.5D时,加速区域宽度为33 m,λ最大值为1.225;横向间距为3D时,加速区域宽度为41 m,λ最大值为1.222。两台水轮机间都出现了水流加速现象,随着横向间距的增大,加速区域宽度增大,但λ最大值会略微降低1.21%,这是因为水轮机和单桩的存在,过流断面面积减小,导致流速出现了一定的增加,随着横向间距的增大,此时单桩和水轮机对水流仍有加速作用,只是作用在不断减小,因此加速区域宽度会不断增大,但是λ最大值会减小。同样地,在来流速度3.7 m/s和4.8 m/s的条件下,对水轮机后方5D处的尾流流速剖面进行研究,发现与2.6 m/s流速时规律基本一致。
同理,研究了各相对安装高度下横向间距对水轮机飞逸转速、各向最大水流作用力以及水轮机尾流流速剖面的影响,发现在不同相对安装高度时飞逸转速几乎不受横向间距的影响。各相对安装高度下横向间距对各向最大水流作用力的影响,与各来流速度下横向间距对各向最大水流作用力的影响基本相似。各相对安装高度下,不同横向间距对水轮机后方的尾流场影响与各来流速度下横向间距对尾流场的影响规律相同。
3 水轮机相对安装高度的影响效应
当横向间距为2D时,水轮机受水流作用力较大且尾流场中λ最大值较大,在工程中属于不利情况。因此,以横向间距2D为例,进一步探讨水轮机相对安装高度对水轮机组水动力特性的影响规律。将水轮机相对安装高度分别设定为0.3、0.5、0.67,来流速度为3.7 m/s,并以1号水轮机为例进行分析。
3.1 对飞逸转速的影响
在不同相对安装高度下,随着水轮机安装高度增加,ω也相应增加,在水轮机相对安装高度分别为0.3、0.5、0.67时,水轮机ω分别为1.21 rad/s、1.61 rad/s、1.78 rad/s。这与流速垂向分布密切相关。水轮机远离海床,水流速度增加,水轮机受到的来流速度也更大了。

表3 不同相对安装高度下水轮机各方向的水流作用力
3.2 对各向最大水流作用力的影响
表3为不同相对安装高度下水轮机在X、Y、Z方向最大水流作用力。随着安装高度增加,水轮机受力F出现明显变化规律。相对安装高度越大,Fx增加相当明显,相对安装高度为0.3~0.67,最大水流作用力增加106.86%,这是由于越靠近自由水面,水流流速越大,因此水轮机受到的水流作用力也会更大;Fy与Y轴负方向相同,这是由于水轮机扇叶旋转的不对称性造成的,其量值随相对安装高度的增大而减小,降幅达12.7%;Fz变化不明显,原因是水轮机Z方向受水流作用力主要是浮力,当在静水中时完全淹没的水轮机在任何安装高度的浮力大小应该是相同的,但相对安装高度的增加导致水轮机叶片旋转面积范围内的流速增加,因此其所受Fz会随相对安装高度的增加而产生微小增量。
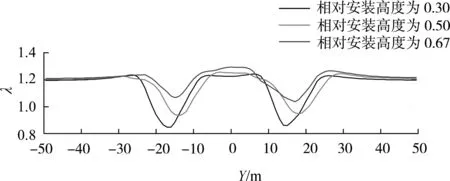
图5 不同相对安装高度下的水轮机后方5D处的尾流流速剖面Fig.5 Distribution of wake flow velocity at5D behind turbine with different relative installation heights
3.3 对水轮机尾流流速剖面的影响
不同的水轮机安装高度对水轮机尾流场的影响很大,因此在横向间距2D和来流速度3.7 m/s条件下分别改变水轮机相对安装高度为0.3、0.5和0.67,分析水轮机后方5D处的尾流流速剖面,如图5所示,在不同相对安装高度下2台水轮机间均出现了水流加速现象。相对安装高度为0.3、0.5和0.67时λ最大值分别为1.232、1.256、1.293,随着相对安装高度增加,λ最大值相应增加,增幅达5%,下游侧的水轮机可获取到更多的能量。
4 来流速度的影响效应
如前所述,横向间距2D时属于不利情况,故以横向间距2D为例,进一步探讨来流速度对水轮机组水动力特性的影响。将来流速度分别设定为2.6 m/s、3.7 m/s、4.8 m/s,水轮机相对安装高度为0.5,并以1号水轮机为例进行分析。
4.1 对飞逸转速的影响
来流速度为2.6 m/s、3.7 m/s和4.8 m/s时,对应的水轮机ω分别为1.13 rad/s、1.61 rad/s、2.13 rad/s。流速从2.6 m/s增大到4.8 m/s,水轮机ω增加了88.50%,可见来流速度的改变对水轮机ω有显著的影响。

表4 不同来流速度时的水轮机各向水流作用力
4.2 对各向最大水流作用力的影响
不同来流速度下,随时间变化的水轮机受力F如表4所示。来流速度对水轮机受力F有重要影响,特别是在X方向和Y方向。随着来流速度增加,水轮机受Fx明显增加,来流速度从2.6 m/s增加到4.8 m/s,增幅达235.58%,由于来流速度沿着X轴正方向,且流速增加明显,因此水轮机所受Fx出现明显增加;Fy与Y轴负方向相同,来流速度增加,受力显著增加,增幅达325.15%,由于来流速度增加,使水轮机间的水体紊动增强,导致Fy明显增加。在Z方向,随着来流速度增加,受力有一定程度的增加,但增幅较小,原因是水轮机Z方向受水流作用力的主要组成部分是浮力,浮力随流速变化而产生的变化是较小的。

图6 不同来流速度下的水轮机后方5D处的尾流流速剖面Fig.6 Distribution of wake flow velocity at 5D behind turbine with different incoming velocities
4.3 对水轮机尾流流速剖面的影响
在横向间距2D下,当水轮机相对安装高度为0.5时,分别改变来流速度为2.6 m/s、3.7 m/s、4.8 m/s,研究水轮机后方5D处的尾流场情况。如图6所示,在不同来流速度下,两台水轮机间均出现了水流加速现象,当来流速度分别为2.6 m/s、3.7 m/s和4.8 m/s时,最大流速无量纲值分别为1.237、1.256、1.283,随着来流速度增大,λ最大值越大。
5 结 语
采用FLOW-3D软件建立三维水动力计算模型,模拟分析2台并排布置的水平轴潮流能水轮机组的水动力特性,研究横向间距、水轮机相对安装高度和来流速度对水轮机飞逸转速、最大水流作用力和尾流流速剖面的影响。
a.ω受横向间距的影响较小;Fx随横向间距的增大有一定的减小,Fy受横向间距的影响较大;2台水轮机间出现了水流加速现象,尾流场中λ最大值随横向间距的增大而略有减小。
b.水轮机的相对安装高度增加,水轮机组的飞逸转速有较大提高;Fx显著增加;Fy会有较大幅度减小,在三种相对安装高度下,两台水轮机间的水流均出现加速现象,λ也随之增加。
c.来流速度增大,水轮机飞逸转速有明显增加,Fx、Fy增强显著,2台水轮机间的λ最大值也随之增加。
[1] 张亮, 李新仲, 耿敬, 等. 潮流能研究现状2013[J]. 新能源进展, 2013, 1(1): 53-68. (ZHANG Liang, LI Xinzhong, GENG Jing, et al. Study status of tidal current energy 2013[J]. Advances in New and Renewable Energy,2013, 1(1): 53-68. (in Chinese))
[2] ZHANG Jisheng, WANG jun, TAO Aifeng, et al. New concept for assessment of tidal current energy in Jiangsu Coast, China[J]. Advances in Mechanical Engineering, 2013, 5: 340501.
[3] HAYDAR F H, AHMED E S, OTHMAN A K. Tidal current turbines glance at the past and look into future prospects in Malaysia[J]. Renewable and Sustainable Energy Reviews, 2012, 16(8): 5707-5717.
[4] 魏东泽, 吴国荣, 郭欣, 等. 潮流能开发技术研究进展[J]. 可再生能源, 2014, 32(7): 1067-1074.(WEI Dongze, WU Guorong, GUO Xin, et al. Advance in tidal current energy development technology[J]. Renewable Energy Resources, 2014, 32(7): 1067-1074. (in Chinese))
[5] MYCEK P, GAURIER B, GERMAIN G, et al. Experimental study of the turbulence intensity effects on marine current turbines behaviour. Part 2: two interacting turbines[J]. Renewable Energy, 2014, 66(7):876-892.
[6] 张亮, 尚景宏, 张之阳,等. 潮流能研究现状2015:水动力学[J]. 水力发电学报, 2016, 35(2):1-15. (ZHANG Liang, SHANG Jinghong, ZHANG Zhiyang, et al. Study status of tidal current energy 2015:hydrodynamics[J]. Journal of Hydroelectric Engineering, 2016, 35(2):1-15. (in Chinese))
[7] LI Linjuan, ZHENG Jinhai, PENG Yuxuan, et al. Numerical investigation of flow motion and performance of a horizontal axis tidal turbine subjected to a steady current[J]. China Ocean Engineering, 2015, 29: 209-222.
[8] MCADAM R A, HOULSBY G T, OLDFIELD M L G. Experimental measurements of the hydrodynamic performance and structural loading of the Transverse Horizontal Axis Water Turbine: Part 1[J]. Renewable Energy, 2013, 59: 105-114.
[9] MCADAM R A, HOULSBY G T, OLDFIELD M L G. Experimental measurements of the hydrodynamic performance and structural loading of the Transverse Horizontal Axis Water Turbine: Part 2[J]. Renewable Energy, 2013, 59: 141-149.
[10] MCADAM R A, HOULSBY G T, OLDFIELD M L G. Experimental measurements of the hydrodynamic performance and structural loading of the Transverse Horizontal Axis Water Turbine: Part 3[J]. Renewable Energy, 2013, 59: 82-91.
[11] 张亚超, 姚炎明, 万猛, 等. 基于不同初始流速和推力系数的水平轴海流机尾流效应的实验研究[J]. 浙江大学学报(工学版), 2014,48(12): 2271-2276.(ZHANG Yachao, YAO Yanming, WAN Meng, et al. Experimental study on the wake effect of horizontal marine current turbine based on different initial velocity and thrust coefficient[J]. Journal of Zhejiang University(Natural Sciences), 2014,48(12): 2271-2276. (in Chinese))
[12] 辛小鹏, 邵雪明, 邓见, 等. 串列布置双转子海流机水动力性能预测[J]. 浙江大学学报(工学版), 2011, 45(7): 1227-1231. (XIN Xiaopeng, SHAO Xueming, DENG Jian, et al. Hydrodynamic performance prediction of tandem dual-rotor marine current turbine[J]. Journal of Zhejiang University (Natural Sciences), 2011, 45(7): 1227-1231. (in Chinese))
[13] MYCEK P, GAURIER B, GERMAIN G, et al. Numerical and experimental study of the interaction between two marine current turbines[J]. International Journal of Marine Energy, 2013, 1: 70-83.
[14] DIVETT T, VENNELL R, STEVENS C. Optimization of multiple turbine arrays in a channel with tidally reversing flow by numerical modelling with adaptive mesh[J]. Philosophical Transactions of the Royal Society A: Mathematical Physical & Engineering Sciences, 2013, 371: 20120251.
[15] STALLARD T, COLLINGS R, FENG T, et al. Interactions between tidal turbine wakes: experimental study of a group of three-bladed rotors[J]. Philosophical Transactions of the Royal Society A: Mathematical Physical & Engineering Sciences, 2013, 371:20120159.
[16] BARKHUDAROV M R. Lagrangian VOF Advection method for FLOW-3D[J]. Flow Science Inc Technical Note FSI03TN63R, 2004, 1: 1-11.
[17] VALERO D, BUNG D B. Sensitivity of turbulent Schmidt number and turbulence model to simulations of jets in crossflow[J]. Environmental Modelling & Software, 2016, 82: 218-228.
Investigation of hydrodynamic characteristics around parallel-arranged horizontal-axis tidal stream turbines
ZHANG Jisheng1, CAO Yunxiu1, WU Xiuguang2, SONG Fan1, DAI Peng1
(1.CollegeofHarbor,CoastalandOffshoreEngineering,HohaiUniversity,Nanjing210098,China;2.ZhejiangInstituteofHydraulicsandEstuary,Hangzhou310020,China)
A three-dimensional (3D) hydrodynamic model was developed based on FLOW-3D. The influences of the lateral spacing and relative installation elevation of the turbines and incoming velocity on the hydrodynamics around two parallel-arranged horizontal-axis tidal stream turbines were investigated. Numerical results show that an increase of the lateral spacing between two turbines leads to a decrease of the maximum fluid force acting on the turbines in the flow direction, with a maximum decrease of 6.62%, and a decrease of the maximum velocity in the accelerating region of the wake field, with a maximum decrease of 1.21%. The changes of relative installation elevation of turbines and incoming velocity have significant impacts on the rotating speed of turbines, maximum fluid force acting on turbines, and the velocity distribution within the wake field.
tidal stream energy; tidal stream turbine; lateral spacing; relative installation height; incoming velocity; hydrodynamics; numerical simulation
10.3876/j.issn.1000-1980.2017.03.011
2016-07-10
国家自然科学基金(51479053);江苏省普通高校研究生科研创新计划(CXZZ13_0259)
张继生(1979—),男,福建晋江人,教授,主要从事潮流能利用工程研究。E-mail:jszhang@hhu.edu.cn
P743.1
A
1000-1980(2017)03-0256-07
