一类含绝对值恒成立问题的解法研究
2017-06-13筅江苏省扬中市第二高级中学陈桂明
筅江苏省扬中市第二高级中学陈桂明
一类含绝对值恒成立问题的解法研究
筅江苏省扬中市第二高级中学陈桂明
我们知道,高三数学教学主要是解题教学,因此解题研究是高中老师必做的功课,下面笔者以一道习题为例,谈谈高中数学解题教学的一些思考.
一、题目呈现
⑴求f(x)在区间[0,1]上的极值;
此题是高三复习时的一道题,题面熟悉,但是学生的解答并不理想.下面针对第(2)问我们来分析学生遇到的困惑.
二、学生的困惑
错误2:从命题的否定入手:
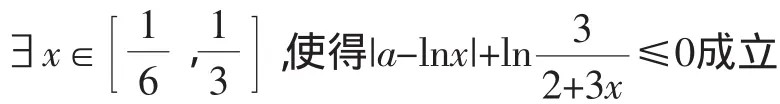

我们知道,解题错误的原因总有其内在的合理性,解题分析首先要对合理成分给予充分的理解;要通过反例或启发等途径暴露矛盾,引发当事者的自我反省;要正面指出错误的地方,具体分析错误的性质;这两种解法思路没有错,那问题到底又出在哪儿?此类问题一般的求解思路又是什么?
错误1利用了结论|f(x)|>g(x)圳f(x)>g(x)或f(x)< -g(x)进行转化,该结论本身并没有错,但在恒成立问题上遇到了麻烦,①到②及③到⑦的转化也都没有问题,问题就出在②到③的转化,也即学生将“坌x∈D,a>f(x)或a 有的同学根据含绝对值的恒成立问题的解决办法:设函数f(x),g(x)的定义域为A,f(x)+g(x)是连续函数,且满足g(x)≥0.则坌x∈A,|f(x)|>g(x)成立的充要条件为坌x∈A,f(x)≥g(x)或坌x∈A,f(x)<-g(x). 其中问题是将“埚x∈D,f(x)≤a≤g(x)成立”圳“”时,未注意到g(x)-f(x)≥0这一前提,从而忽视了x范围的改变.由此题中,即x≥ 解法1:按a分类讨论: 解法3:从命题的否定入手: 1.重视“研”题目,促进深度探究 在平时的教学中,要带着一种研究的态度去做题,深入探究试题解法的多样性,培养学生的发散思维,使得学生能在以后的解题中获得较为合理和简洁的运算途径和思维方法.叶澜教授曾说:“课堂是向未知方向挺进的旅程,随时都有可能发现意外的通道和美丽的因素,而不是一切都必须遵循固定路线而没有激情的行程.”课堂教学过程是复杂的、丰富多变的,难免会遇到超出预设方案之外的新问题、新想法,教师应善待学生提出的“意外”问题,尊重学生的“话语权”,为学生营造一个敢于发表自己见解、勇于说出自己想法的平台,适时调整教学设计方案,为学生的“动态生成”腾出一片广阔的空间,并因势利导,借题“发挥”,提升复习效益.课堂上只有真正放手让学生做,才会为学生创造探究的机会,才能真正发挥学生学习的主观能动性,才能引发学生的认知冲突,激发学生的思维火花,才能更好地做好“研”题目. 2.追求“慢”教学,激活学生思维 为什么会经常出现“听起来头头是道,做起来莫名其妙”的现象,这与平时我们不敢放手课堂,课上老师讲得多,课下学生练得少有很大关系.对数学知识的学习应该是一个循序渐进、不断感悟和深化的过程,因此,数学要追求“慢”教学,要以学生为本,在教学过程中不断设置有利于激发学习潜能,锻炼学生思维的问题和情境,实现课堂效益最大化.另外,数学教学内容的呈现还要利于学生自主探究,在交流互动中体验知识的产生和发展,在思维碰撞中经历数学的发现和创造,只有“慢”教学,才能让知识的剖析更为细腻,让习题的辐射更为广泛,让学生的体验更为深刻,才能更多地为学生提供“说”和“做”的时间和空间.而没有数学思考,就没有真正的数学学习,只有学生通过自己的思考建立起自己的数学理解力时,才可以说对知识达到了较高程度的掌握.故而,课堂上教师应提倡“慢”教学,尊重学生的“第一思考权”,尊重学生的认知规律,以“学为中心”展开教学过程,多给学生“想一想”的时间,多给学生数学思维锻炼和表达的机会.因此,课堂教学应当使学生身心处于和谐宽松的教学生态中,从学生的眼神中读出内心的感受,从学生的表情上看出思维的起伏,从学生的言行中评估教学成效,从师生的互动交锋中演绎教学的精彩,这一切都需要教师在教学活动中等待、耐心、从容、宽容、期待、优雅,数学课堂“慢”教学的生态性注重学生心理感受、成功体验、快乐成长,“慢”在教学中是一种心境,更是一种艺术,也是孕育教学动态生成的精彩历程.三、拓展探究
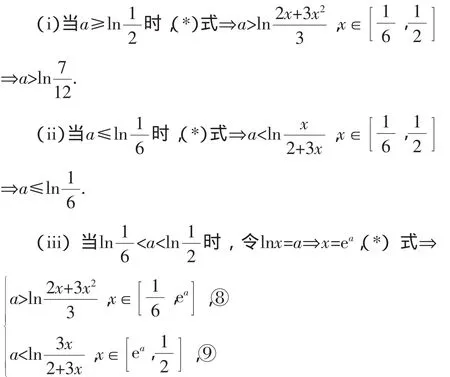
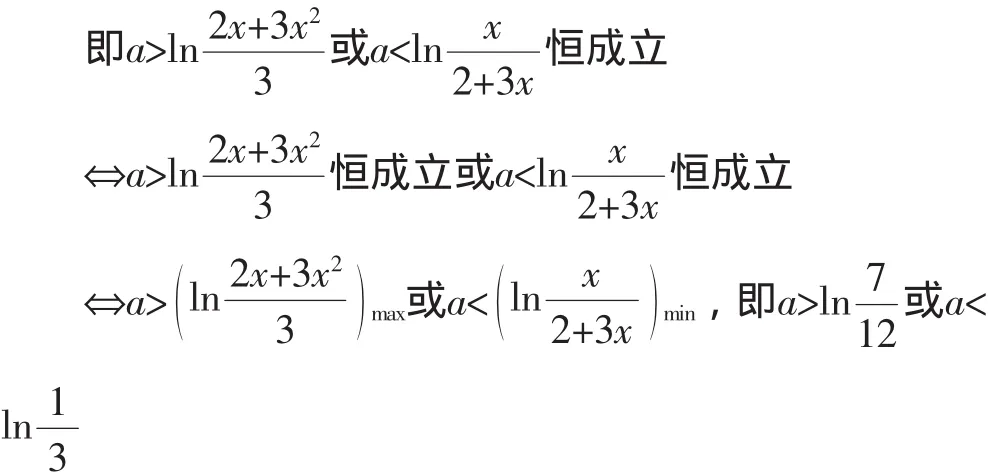

四、几点思考
