一类圆锥曲线定点问题的多视角探究
2017-06-13筅浙江省诸暨市海亮高级中学沈铁表
筅浙江省诸暨市海亮高级中学沈铁表
一类圆锥曲线定点问题的多视角探究
筅浙江省诸暨市海亮高级中学沈铁表
同一类型的问题,其解法往往有其规律性,要想减轻课业负担,从题海中解脱出来,必须学会在解题后对问题的求解方法、常见变式进行探究,并发现归纳知识间的内在联系,挖掘出数学思想与方法,总结概括出解题的基本规律.这样,既有利于对问题的认识上升到一个更高层次,又有利于概括思维能力的训练和培养.
例1在平面直角坐标系xOy中,动点E到定点(1,0)的距离与它到直线x=-1的距离相等.
(1)求动点E的轨迹C的方程;
(2)设动直线l:y=kx+b与曲线C相切于点P,与直线x=-1相交于点Q.证明:以PQ为直径的圆恒过点M(1,0).
解析:(1)y2=4x.(过程略)
设切点P(x0,y0),
故以PQ为直径的圆恒过定点(1,0).
点评:以PQ为直径的圆恒过定点M,则有MP⊥MQ,从而可利用向量数量积为0或斜率之积为-1来求解.
下面从多个视角对此类定值问题进行探究.
一、改变求解结论
例2在平面直角坐标系xOy中,动点E到定点(1,0)的距离与它到直线x=-1的距离相等.
(1)求动点E的轨迹C的方程;
(2)设动直线l:y=kx+b与曲线C相切于点P,与直线x=-1相交于点Q.证明:以PQ为直径的圆恒过x轴上某定点.
解析:(1)y2=4x.(过程略)
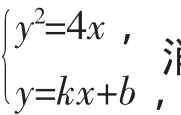
(2)联立消去x得ky2-4y+4b=0,因为直线l与抛物线相切,所以Δ=16-16kb=0,即b=,所以直线l的方程为y=kx+.
点评:本题将所求结论改为定点的探索型问题,求解的关键是找出满足条件的参数关系式,即可判定所过的定点.
二、改变求解策略
例3同例2.
解析:(1)y2=4x.(过程略)
设切点P(x0,y0),则
令k=1,则P(1,2),Q(-1,0),PQ中点为(0,1),|PQ|=,所以以PQ为直径的圆的方程为x2+(y-1)2=2.令y=0,得x=1,所以圆与x轴的交点为M(1,0).下面证明M(1,0)即为所求的定点.

故以PQ为直径的圆恒过x轴上的定点(1,0).
点评:本解法通过取k的特殊值,将圆的方程特殊化,从而得出该圆与x轴的交点,再通过证明该点即为所求的定点.这种从特例入手,验证一般的处理方法,既能快速明确目标,又减少了大量的繁杂计算.
三、改变曲线类型
(1)求椭圆E的方程;
(2)设动直线l:y=kx+m与椭圆E有且只有一个公共点P,且与直线x=4相交于点Q.试探究:x轴上是否存在定点M,使得以PQ为直径的圆恒过点M?若存在,求出M的坐标;若不存在,说明理由.
因为动直线l与椭圆E有且只有一个公共点P(x0,y0),所以m≠0且Δ=0,即64k2m2-4(4k2+3)(4m2-12)=0,化简得4k2-m2+3=0.①
设M(x1,0),则对满足①式的m,k恒成立.
由于②式对满足①式的m,k恒成立,即与m,k的取值无关,故整理成(4x1-4)
故存在定点M(1,0),使得以PQ为直径的圆恒过定点M.
若满足条件的点存在,则定点为M(1,0)
下面只需验证点(1,0)是否符合题目条件即可.
故存在定点M(1,0),使得以PQ为直径的圆恒过点M.
点评:圆锥曲线包括椭圆、双曲线和抛物线,三者具有统一的定义,因此对于某一曲线所具有的性质,可类比迁移到其他曲线,通过对问题的探究,可以有效提高学生分析、处理问题的能力.
综上,圆锥曲线中的定点问题看似没有规律和联系,事实上只要我们作深入思考,就不难发现其中的奥秘和内在的规律.只要掌握这些规律和联系,解决这类问题就显得很简单了.通过对这类问题的探究,不仅学会了一类知识,还会大大提高学生的解题能力.F
