数学归纳法在几何解题中的应用
2017-06-13筅湖北省武汉市第二中学张搏翰
筅湖北省武汉市第二中学张搏翰
数学归纳法在几何解题中的应用
筅湖北省武汉市第二中学张搏翰
一、数学归纳法简介
定理1(第一数学归纳法定理)设p(n)表示任意一个与自然数n有关的命题,并满足:若p(0)、p(1)成立,且有p(n)→p(n+1),则对于任意的自然数n,p(n)恒成立.
定理2(第二数学归纳法定理)设p(n)表示任意一个与自然数n有关的命题,并满足p(1)成立,若n≤k时命题成立,可以推导得n=k+1时命题成立,则对于任意的自然数n,p(n)恒成立.
二、数学归纳法在几何解题中的应用
1.数学归纳法在中学几何问题绘图中的应用
数学归纳法在几何绘图中的应用主要在绘制平面几何图形的中心和重心等方面.理论上来说,不管多么复杂的平面多边形,都可以通过尺规作图的方式得到平面多边形的中心和重心.比如,三角形可以通过三边中线的交点得到重心,而四边形则可以通过分别连接两个对点构造两个三角形得到两个重心连线,其交点即为四边形的重心.但是当边数逐渐增多时,很难通过尺规直接绘制平面几何的重心,因此需要用数学归纳法,举例如下:
例1假设平面上现有2n+1个点,试作一个(2n+1)边形,恰好以这2n+1个点为中点.
解析:当n=1时,将上述问题可归纳为:平面上3个点,试作三边形恰以这3个点为中点.此时,将3点分别两两连线,再过每点分别作连线的平行线即可.
假设当平面上有2n-1个点时,可以得到一个(2n-1)边形,恰以这2n-1个点为中点,并假设平面上有2n+1个点A1,A2,…,A2n+1,要作一个(2n+1)边形,恰好以这2n+1个点为中点.
考虑平面上四边形X1X2n-1XnX2n+1,如图1,点A2n-1,A2n,A2n+1是它各边X2n-1X2n、X2nX2n+1、X2n+1X1的中点.
假设A是边X1X2n-1的中点,则四边形AiA2n-1A2nA2n+1是平行四边形.
由于三个顶点A2n-1、A2n和A2n+1是已知的,所以平行四边形的第四个定点容易得到.
点A1,A2,…,A2n-2,A是(2n-1)边形X1X2…X2n-1的中点,根据假设,这个(2n-1)边形可以得到,因此只需再作出以点A2n+1和A2n-1为中点的线段X1X2n+1和X2n-1X2n.

图1
2.数学归纳法在中学几何问题运算中的应用
求边或角的数值,以及平面几何中边、角构成的不等式,占所有平面几何问题的三分之二,数学归纳法在几何计算中的应用主要在于涉及多个平面几何图形的边或角或弧的运算,或求多个几何图形边、角、弧、个数构成的不等式计算,举例如下:
例2设有多个圆心在同一条直线一边且两两相交的半圆,试求这些半圆的交点最多将半圆分割成多少个圆弧?
解析:设半圆个数与圆弧个数为函数f(n),则容易验证,当n=2时,f(n)=f(2)=4=22,如图2所示:
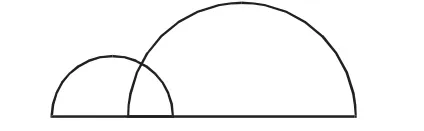
图2
当n=3时,为了使得到的圆弧最多,应将第三个半圆和前两个半圆都相交,得到f(n)=f(3)=9=32.
因此,设当有n个半圆时,可以将半圆最多分成f(n)=n2个圆弧.
证明如下:当n=2时命题成立.假设当n=k时命题成立,即当直线一边有k个两两相交的半圆时,可以把圆弧分割成k2个圆弧.
当n=k+1时,且第k+1个半圆与原来的第k个半圆都相交时可以得到最多的圆弧.
此时,第k+1个半圆将原来所有的半圆都割出了一条新圆弧,有k条圆弧,而原来所有的半圆将第k+1个半圆分割成了k+1个圆弧,因此f(k+1)=k2+k+k+1=(k+1)2,即当n=k+1时命题成立.
根据归纳法原理,该命题是真命题,即设当有n个半圆时,可以将半圆最多分成f(n)=n2个圆弧.
3.数学归纳法在中学几何问题论证中的应用
论证题,是中学数学中最常见的几何题类型,也是很多学生最头疼的几何题类型.不少学生看到需要证明的几何题,往往不知道从何下手.数学归纳法在中学几何证明题中的应用集中在有n个几何图形的情况.举例如下:
例3假设有n条互不平行的直线在同一个平面内,且其中任意的三条直线没有交点,试证明这n条直线可以将其所在平面分割成个小区域.
证明:当n=1时,即平面内只有一条直线,可以把平面分割成两个区域,因此有,命题成立.
假设当n=k时命题成立,即当有k条互不平行的直线在同一个平面内,且其中任意的三条直线没有交点时,这k条直线可以将其所在平面分割成个小区域.
那么,当n=k+1时,这条直线被原来所有的直线分为k+1条线段,每条小线段又将其所在的小区域分为两个,所以会增添k+1个小区域.
因此,当有k+1条互不平行的直线在同一个平面内,且其中任意的三条直线没有交点时,这k+1条直线可以将其所在平面分割成个小区域.所以当n=k+1时命题也成立.根据第一数学归纳法定理,该命题成立.
除上述平面几何问题外,数学归纳法也适用于部分立体几何题目.例如选修课本第二册关于通过平面几何中的勾股定理,猜想空间中四面体的性质.甚至推广到空间中更多面的几何体,就需要运用数学归纳法的思想.
三、结束语
数学归纳法和几何作为中学阶段重要的知识点,相互之间也存在着关系.本文一方面通过举例验证了数学归纳法在平面几何问题绘图、运算和论证中应用的可行性,得到数学归纳法适用于求解涉及多个图形的几何问题的结论.另一方面,给出了数学归纳法在立体几何应用中的研究方向.
1.张德峰.高中数学解题方法中思维品质的培养[J].数学学习与研究,2010(9).
2.肖海燕,代钦.数学归纳法在几何教学中的应用[J].内蒙古师范大学学报,2011.
3.张懿慧.数学归纳法在几何学中的应用[J].教育经验与德育园地,2010.F
