从高考谈圆锥曲线优化教学
——以2015年高考数学浙江卷为例
2017-06-13筅江苏省常熟市尚湖高级中学余志峰
筅江苏省常熟市尚湖高级中学余志峰
从高考谈圆锥曲线优化教学
——以2015年高考数学浙江卷为例
筅江苏省常熟市尚湖高级中学余志峰
高考注重圆锥曲线综合性的考查,研读各地的高考卷,题型设计精妙,注意区分基础与能力,对教学也带来了好的启示,尤以灵活变通最为重要.我们在教学过程中需要加强学生对数学方法的学习和感悟,引导学生结合自身寻求优解.
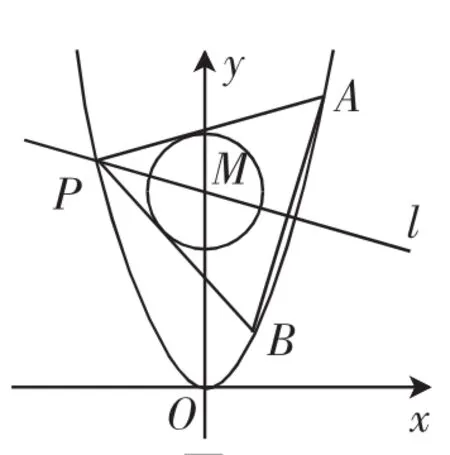
图1
一、考题及思路突破
考题1(2015年浙江高考卷)如图1所示,现有一抛物线C1:x2=y,圆C2:x2+(y-4)2=1,它的圆心为点M.
(1)求圆心点M到抛物线C1准线的距离;
(2)已知有一点P是抛物线C1上一个异于原点的一点,现经过点P作圆C2的切线段,并且使切线交抛物线C1于点A和B,如果经过M和P两点的直线l垂直于AB,求直线l的方程.
1.思路突破
(2)求解直线l方程的途径很多,其中有:①M的坐标已知,设直线l的斜率为k,利用斜率求方程;②利用两点式,设P的坐标然后求解;③确定AB的斜率,然后确定要求的斜率,分析后再求解.对比总结发现途径①需求P的坐标,再求切线方程会复杂,过A、B两点的斜率计算量太大,途径②则较为简单,途径③实际上行不通.则以途径②求解为主,由P点出发,设出切线的斜率,设P(x0,),A(x1,),B(x2,),根据题意有x0≠±1,x1≠x2.设经过P点的圆C2的切线的方程为y-x0=k(x-x0),即y-=k(x-x0),则
设PA、PB的斜率分别为k1、k2(k1≠k2),那么k1、k2则是上面方程的两个解,所以有但因为P点的坐标已表示出,一元二次方程有一个根已知,则另一个根可以表示出,那么直线AB的斜率可确定,根据两条直线相互垂直的空间关系,可以建立方程,解得,所以点P的坐标为
2.考题拓展
考题2(2015年北京卷)已知一抛物线C:y=(x+1)2,又有一圆,它们有一公共点A,并且在点A处两条曲线的切线为同一直线l.
(1)求r的值;
(2)设m、n为异于直线l且与抛物线C及其圆M都相切的两条直线,m和n的交点为D,求点D到直线l的距离.

图2
考题3(2015年陕西卷)如图2所示,曲线C由椭圆C1的上半部分和部分抛物线C2连接而成,其中(a>b>0,y≥0),C2:y=-x2+1(y≤0).C1和C2的公共点为A、B,并且C1的离心率
(1)求a和b的值;
(2)经过点B的直线l和C1、C2分别相交于P和Q(他们均异于点A和B),如果存在AP⊥AQ,求直线l的方程.
考题4(2016年杭州市三模)如图3所示,已知抛物线E:y2=x,圆M:(x-4)2+y2=r2(r>0),抛物线和圆相交于A、B、C、D四个点.
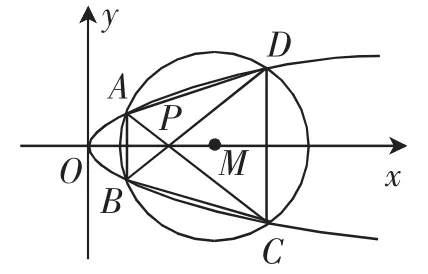
图3
(1)求r的取值范围;
(2)当四边形ABCD的面积达到最大值时,求两条对角线AC和BD的交点P的坐标.
3.对比揭示
上述四题都是对圆锥曲线的考查,曲线组合多种多样,有考查圆和抛物线的,也有椭圆和抛物线的,位置关系有相交也有相切的.解题时都需要通过曲线间的位置关系表示出直线方程,对方程施加限制条件来推理求解,所不同的是考题中的条件有垂直关系,也有共线,面积最大等情况.总体的求解思路都是不变的,结合点线的相互关系列方程,根据条件解未知.
二、教学思考
1.解析高考,活学活用
从高考试题的知识点来看,高考考查内容一般都是高中知识的重点,不会偏离,题型新但不会怪.高考难题的设问也考虑大多数考生,采用一题多问的形式,尤其是综合型很强的题型.在对圆锥曲线的考查中既有针对基础知识的考查,又有综合活用的考核,一般第一问突出考查学生对数学主干知识的掌握,较为简单,第二问则注重学生灵活使用方法,综合知识求解的能力.高考对圆锥曲线考查题型主体不变,通常将直线、三角形、曲线等几何对象进行综合,在结合相关的知识进行考核,求解方法灵活多样,大同小异,需要学生自身多加总结思考,灵活解题.教学中则需要老师注重基础,努力引导,力求避免灌输式教学,多进行新情境下灵活转化,活用方法的指导.
2.扎实基础,提高能力
解题能力的提高是教学的重点,只有基础扎实、解题步骤扎实、运算准确才可以取得高分,运算能力是中学的重点,例如对公式的使用、变形、推理是高中的基础,需要学生在大量的、反复的练习中提高.老师则要努力引导学生进行针对性学习,优化解题方法,例题第二问的解法思路有很多,但是在具体的实施过程中最优解只有一种.在教学中需要引导学生进行反思、体验、总结,掌握常用的解题方法,例如设而不求、整体代换、数形结合等思想方法.解题不在于量,在于精华的汲取,要让学生在熟练基本解题方法的基础上,努力寻求最合理、最简便的方法,不满足于“能解题”,而要追求“会解题”,逐步地提升解决综合性强、难度大的题型的能力.
3.回顾反思,突破陈规
每一道经典题目都有其精华之处,每一次的复习都需要学生进行归纳总结,高考之路其实就是一次次的反思总结的过程.在教学中非常有必要对教授过的题目进行重新的分析思考,多设问多引导,让学生在一次次的思考中加深印象,对比分析中感悟数学思想,进行重新的知识构架的调整,获得思想上的融会贯通,摒弃陈旧的不适合的解题陋习,去突破常规.学会对具体问题具体分析,寻求适合自己的解题方法,积累自己的解题经验,而老师在这个过程中要作为一个引导者,适时的放手,让学生自己完成这个升华的过程.突破常规不是一个简单的过程,需要学生亲自去总结、去积累、去感悟.
三、结束语
圆锥曲线是高考重点考查的一类综合题型,解题方法和思路也是多种多样的,我们应该引导学生去扎实基础,感悟其中的数学思想,通过自我意识的强化达到触类旁通的境界,鼓励学生回顾反思,寻求优解,活学活用,提高解题能力.
1.张进华.既要夯实“通性通法”,又要学会“灵活变通”——从两道高考试题的解法谈起[J].中学数学(上),2016(9).
2.董义.优化解题方法提升运算能力——谈圆锥曲线中椭圆问题的求解方法[J].中学数学(上),2016(9).
3.钟顺荣.利用伸缩变换求解直线与椭圆相切问题初探[J].中学数学(上),2015(3).
4.刘志有.高中数学圆锥曲线教学的有效性策略分析[J].数学教学通讯,2014(15).
5.洪平锋.圆锥曲线互相垂直切交点的一个性质——一道2014年广东高考试题的推广[J].数学教学通讯,2014(6).F
