例谈高考中对函数零点的考查
2017-06-13筅江苏省张家港市崇真中学张雪玲
筅江苏省张家港市崇真中学张雪玲
例谈高考中对函数零点的考查
筅江苏省张家港市崇真中学张雪玲
零点问题是近几年高考考查的热点问题之一,其涉及数形结合、分类讨论、转化与化归、函数与方程等多种数学思想.函数零点也是高中数学中的重要知识点,本文笔者通过平时的教学实践谈谈一些高考中对函数零点问题的考查.
考查一、零点可求——求解具体的零点
当问题的实质是求函数零点或导函数零点时,别无选择,必须把零点用解方程办法算出来.
(1)略.
(2)若f(x)在[3,+∞)上为减函数,求a的取值范围.
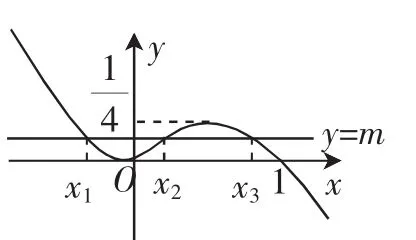
当x 当x1 当x>x2时,f′(x)<0,故f(x)为减函数. 点评:函数的单调区间以极值点为界,而极值点又是其导函数的零点,故以导数为工具研究函数的单调性有关问题,常需要计算导函数的零点. 有的问题没有涉及零点的值,只考查零点的个数,则可以将零点画出.有的基本初等函数画出图像比较容易,而较复杂的函数,则要借助导数,通过求导研究函数的单调性等性质,再画出示意图. 例2设函数f(x)=(x-2)ex+a(x-1)2. (1)若f(x)有两个零点,求a的取值范围; (2)略. 解析:(1)由f(x)=0圯a(x-1)2=(2-x)ex. 显然x=1时,a不存在,故x≠1. 所以函数g(x)在(-∞,1)内单调递减,在(1,+∞)内单调递增. 又x≥2时,g(x)≥0,x<2时,g(x)<0,且g(0)=-2. 在同一坐标系中作出直线y=-a及函数y=g(x)的图像.由图1不难得到a的取值范围为(0,+∞). 点评:由此可见,通过画图得到函数的零点简单直观,避免了烦琐的讨论. 图1 有时所给的零点问题仅仅靠画图像无法顺利解出,此时可以先通过图像探路,再利用严密的逻辑思维进行推导. 图2 x1是关于x的方程2x2-x=m,即2x2-x-m=0的较小根. 故x1x2x3的取值范围是 点评:本题蕴含了函数方程、数形结合、转化化归等数学思想,通过画图和推演结合,将问题完美解决. 若涉及的问题是超越方程对应的问题,通过零点存在性定理我们知道函数在某一区间内有零点时,但是解不出来,此时我们不妨采用先设出零点,再利用等式反代入的方法来解决. 例4设函数f(x)=e2x-alnx. (1)讨论f(x)的导函数f′(x)零点的个数; 解析:(1)当a>0时,方程g(x)=a有一个根,即f′(x)存在唯一零点; 当a≤0时,方程g(x)=a没有根,即f′(x)没有零点.(具体解答过程略) (2)由(1)可设f′(x)在(0,+∞)内的唯一零点为x0,当x∈(0,x0)时,f′(x)<0;当x∈(x0,+∞)时,f′(x)>0.故f(x)在(0,x0)内单调递减,在(x0,+∞)内单调递增,所以f(x)min=f(x0). 由f′(x0)=0,得 (Ⅱ)已知函数f(x)在[-1,1]上存在零点,0≤b-2a≤1,求b的取值范围. 解析:依题意0≤b-2a≤1,得2a≤b≤2a+1,所以x2+ ax+2a≤x2+ax+b≤x2+ax+2a+1,即x2+ax+2a≤f(x)≤x2+ax+ 2a+1. 在解决某些含参变量的函数问题时,常常利用不等式的放缩,采取两边夹法则解决. 例5设函数f(x)=x2+ax+b(a、b∈R). 令g(x)=x2+ax+2a,h(x)=x2+ax+2a+1,则g(x)恒过点(-2,4),h(x)恒过点(-2,5).考虑到三个函数都具有相同的对称轴,因此要使f(x)在[-1,1]上有零点,则函数g(x)向上平移至h(x)的过程中有零点,即与x轴有交点(如图3).要使g(x)在[-1,1]上有零点,则解得-1≤a≤0,此时b=2a,所以-2≤b≤0,要使h(x)在[-1,1]上有零点,则解得-2≤a≤4-2,此时b=2a+1,所以-3≤b≤9- 图3 点评:其实,本题完全可以用前面介绍的方法(零点算出来或零点画出来)加以解决,但都不如上述方法简单,笔者旨在说明:一种漂亮解法的得出,需要我们对以往解题经验的不断积累,更需要我们对问题有深层剖析,它值得我们学习和借鉴. 导数是研究函数性质的重要工具,应用导数研究函数零点,要综合运用函数的性质,比如对称性、特殊点,当然,说明函数在区间(a,b)上存在零点,要根据零点存在定理.下面结合具体问题分析运用导数研究函数零点问题的常用方法和难点. (1)判断函数f(x)的奇偶性,并证明你的结论; (2)求集合A={x|f(x)=0}中元素的个数; (3)当1 解析:(1)函数f(x)是偶函数,证明略. (2)方法1:(研究函数自身的零点) 当a>0时,因为f(x)=acosx+xsinx>0成立,所以集合A={x|f(x)=0}中元素的个数为0. 当a<0时,因为f′(x)=-asinx+sinx+xcosx=(1-a)sinx+,所以函数f(x)是上的增函数. 由f(x)是偶函数可知,集合A={x|f(x)=0}中元素的个数为2. 综上所述,当a>0时,集合A={x|f(x)=0}中元素的个数为0;当a=0时,集合A={x|f(x)=0}中元素的个数为1;当a<0时,集合A={x|f(x)=0}中元素的个数为2. 方法2:(参变分离,转化为判断两个函数的交点个数) 综上所述,当a>0时,集合A={x|f(x)=0}中元素的个数为0;当a=0时,集合A={x|f(x)=0}中元素的个数为1;当a<0时,集合A={x|f(x)=0}中元素的个数为2. (3)略. 以函数零点相关问题作为高考压轴大题,就是因其综合性极强,思想内涵丰富(函数方程,转化化归,数形结合,分类整合等),有很好的选拔功能,有难度是必然的,但只要我们从数形两方面思考,破解这类问题,应该没有问题.F考查二、考查图像——画出具体零点

考查三、数形结合——计算零点与画出交点相结合
考查四、设而不求——虚设出零点
考查五、构造函数——两边夹法则
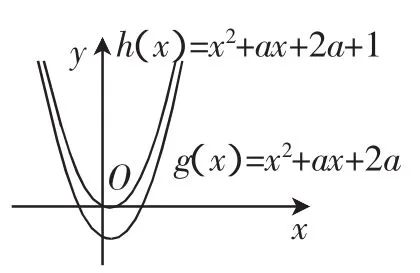
考查六、应用导数研究函数零点问题
