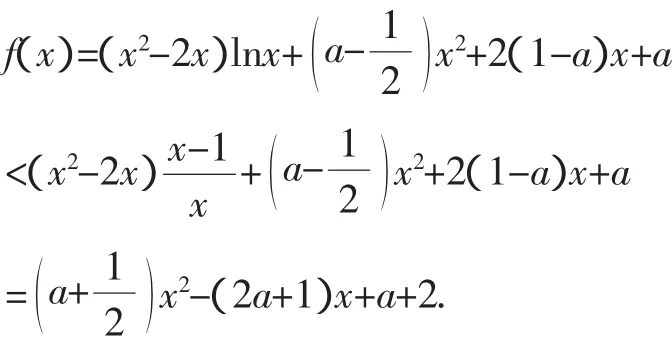导数题运算的关键在于“运”
2017-06-13筅新疆兵团二中徐波
筅新疆兵团二中徐波
导数题运算的关键在于“运”
筅新疆兵团二中徐波
高考“考试大纲”指出:“运算求解能力是思维能力和运算技能的结合,运算能力包括分析运算条件,探究运算方向,选择运算公式,确定运算程序等一系列过程中的思维能力,也包括在实施运算过程中遇到障碍而调整运算的能力.”[1]这些对运算能力的要求都贯穿落实在高考、模考试卷的导数压轴题的考查中,运算求解能力与推理论证能力、创新意识等能力综合发挥效应全方位地体现在导数压轴题的求解过程中,达到了对考生的数学综合素养进行深层次考查的目的,[2],[3]因此,高考、模考试卷中的导数压轴题承担着整个试卷的把关重任,有着良好的区分度,在选拔性考试中肩负着重要的任务.笔者根据多年来研究高考新课标卷试题和多年来参加乌鲁木齐市高三模考命题的实践,结合多年来在教学中辅导高三学生高考复习备考的课堂教学实践,深刻意识到解决导数压轴题的关键在于运算.而运算的关键在于“运”,就是“运筹”、“运转”,整个的解题进程和解题方案的形成背后其实都是受运算进程支配的,运算在当中起着决定性作用.由于笔者有多年来一直参加乌鲁木齐市高三模考命题工作的经历,因此,笔者特意选择了2017年乌鲁木齐市高三第三次诊断性测试(最近刚举行的测试)的试题作为本文的素材来展开论述.为了增加实用性,在例题后面又附了一道相应的练习题.希望本文的观点和方法能够对老师的教学和同学们的学习有一点帮助.
(1)讨论f(x)的单调性;
(2)当a<-2时,讨论f(x)的零点个数.
分析:(1)用导数来研究函数f(x)的单调性:f′(x)= 2(x-1)lnx+(x-2)+(2a-1)x+2(1-a),
f′(x)=2(x-1)·(lnx+a)(x>0).
(i)当a=0时,f′(x)=2(x-1)lnx,当0
当x>1时,f′(x)>0,当x=1时,f′(x)=0,
所以f(x)在(0,+∞)上单调递增.
(ii)当a>0时,令f′(x)=0,得两个根x1=1,x2=e-a,
此时e-a<1,根据f′(x)的正负容易判断出函数f(x)的单调性:
f(x)在(0,e-a)上单调递增,(e-a,1)上单调递减,(1,+∞)上单调递增.
(iii)当a<0时,此时e-a>1,
则f(x)在(0,1)上单调递增,在(1,e-a)上单调递减,在(e-a,+∞)上单调递增.
(2)当a<-2时,由(1)可知,f(x)在(0,1)上单调递增,(1,e-a)上单调递减,在(e-a,+∞)上单调递增,
再将x=e-a代入函数f(x):

所以f(e-a)<0,
根据函数零点存在定理,结合函数的单调性,可知f(x)在(1,e-a)内存在唯一的一个零点.
接下来探究f(x)在(0,1)内的零点情况,已经有f(1)>0,而f(0)没有意义,我们只能考察当x→0+时函数值f(x)的状态,这需要用极限来考察,把函数值f(x)分成两部分来考察,先看,由此我们合情推理在0+附近存在x0,使f(x0)<0,这样f(x)在(0,1)内应该是有一个零点的.下面证明:当x∈(0,1)时,存在x0,使f(x0)<0,
首先(fx)=(x2-2x)lnx+∈a-∈x2+2(1-a)x+a里含有一个超越式和一个代数式,根本没法沟通没法运算(没有这方面的运算律支持),现在的主要矛盾就卡在运算上!其实我们只是想在0+附近找到一个x0,使f(x0)<0,那我们可以在0+附近把f(x)稍微放大一些,使得放大以后再小于0,在这个将f(x)放大一些的过程中,就可以改变f(x)的代数结构,使得原本一个超越式和一个代数式没法运算的局面得以改观,因此我们首先想着将lnx“变成”一个有理函数,总的来说,我们是要探求“f(x)<?”,考虑到在0+附近x2-2x=x(x-2)<0,因此我们只需要探求“lnx>?”,然后在它两边同时乘以“x2-2x”,就能得“(x2-2x)·lnx<?”,但是这个任务不好办,因为我们的经验是lnx≤x-1(这是一个常用的不等式,很容易证明),怎么变成“lnx>?”呢,这就需要运算律方面的智慧和策略了!以“”代入lnx 最后探究f(x)在(e-a,+∞)内的零点情况,前面已经知道f(e-a)<0,我们还需要考察当x→+∞时函数值f(x)的状态,这需要用极限来考察,如果还像前面那样把函数值f(x)分成两部分来考察的话,先看,还是看不出来当x→+∞时函数值f(x)的状态,然而从合情推理的角度,(x2-2x)lnx是一个二次函数乘以一个“+∞级别”的函数lnx,而是一个二次函数乘以一个负的系数“a-”,二者“较量”的结果应该还是(x2-2x)lnx“占上风”,所以,当x→+∞时函数值f(x)→+∞,也就是说在x∈(e-a,+∞)上,一定存在x1,使f(x1)>0,但这毕竟是合情推理,要用逻辑推理的话,我们试试: ,而且在“+∞”附近x2-2x> 0,现在我们可以把f(x)缩小一些: 这时候就需要重新整理函数值f(x)的代数结构,考虑到在+∞附近x2-2x>0,我们把f(x)的后面那一部分二次函数里也提取出来一个x2-2x与前面的项合并,这样将f(x)的函数值的代数结构重新调整成两部分,再让每一部分分别大于零,取其交集,就可以得到一个使f(x)>0的x1了,试试看: 分别令(x2-2x)≤lnx+a-∈>0,① 且x+a>0.② 由②解得x>-a. 根据指数函数与一次函数的关系ex>x+1,容易判断 以上是本题的一个鲜活的思维探究的过程,书面表达出来则是下面这种“冷冰冰”的形式化的表述: (1)f′(x)=2(x-1)(lnx+a)(x>0), 当x>1时,f′(x)>0,当x=1时,f′(x)=0,所以f(x)在(0,+∞)上单调递增. (ii)当a>0时,令f′(x)=0,求得x1=1,x2=e-a,此时e-a<1,根据f′(x)的正负容易判断出函数f(x)的单调性: f(x)在(0,e-a)上单调递增,在(e-a,1)上单调递减,在(1,+∞)上单调递增. (iii)当a<0时,此时e-a>1, 则f(x)在(0,1)上单调递增,在(1,e-a)上单调递减,在(e-a,+∞)上单调递增. 我转过头,视线穿过课桌上高高低低小山般的书堆,落在后面陈浩和朱木澜的座位上,空的,两个人都不在,甚至都没有参加期末考试。过完寒假就是最紧张的高三下学期了,他们两个会回来吗? 考虑到x2-2x=x(x-2)<0, 由零点存在定理及函数f(x)在(0,1)上的单调性可知,f(x)在(0,1)上有唯一的一个零点. 由f(1)>0,f(e-a)<0,及f(x)的单调性可知,f(x)在(1,e-a)上有唯一零点. 下面证明在x∈(e-a,+∞)上,存在x1,使f(x1)>0,取x1=,则x1>e-a, 由不等式ex≥x+1,则e-a+a≥(-a+1)+a>0,即f(x1)>0. 根据零点存在定理及函数单调性可知,f(x)在(e-a,+∞)上有一个零点. 综上所述,当a<-2时,f(x)共有3个零点. (1)讨论f(x)的单调性; (2)证明当a≥0时,f(x)>0. 在导数压轴题中的运算过程中,常常需要借助函数的麦克劳林展开式,将一个超越函数用一个多项式形式的函数去取代,最常用的是ex≥x+1和lnx≤x-1,有的时候甚至还需要作一些变量代换,进一步获得我们所需要的一些有理函数的形式.比如,以“”代入lnx≤x-1中,可得,这一切都是为了将运算调整到能够进行下去的轨道上去.在平常的解题教学中,每当碰到运算进行不下去或者出现运算的关键转折处时,要停下来,把学生难在那里,先让他们充分地体验运算的阻力所在和关键所在,教师不要在这些地方好心地全盘托出,毫无阻力,那样学生什么都没学到,没有发生应有的成长.教师只需要在恰当的时机给予点拨引导,提炼解决问题的关键思路、关键技术.使学生明确探究解题方案的进程的背后其实都是受运算进程的支配,运算在当中起着决定性的作用.总之,教师不能包办代替学生的成长,而这样一个基本的教学理念落实起来仍然还任重道远. 1.教育部考试中心.《2016年普通高等学校招生全国统一考试大纲》[M].北京:高等教育出版社,2015. 2.教育部考试中心.《2016年普通高等学校招生全国统一考试大纲的说明》[M].北京:高等教育出版社,2015. 3.教育部考试中心.《高考理科试题分析》(2016年版)[M].北京:高等教育出版社,2015.