高中生数学推理能力的调查研究
2017-06-13筅甘肃省酒泉中学李自敏
筅甘肃省酒泉中学李自敏
高中生数学推理能力的调查研究
筅甘肃省酒泉中学李自敏
一、问题提出
高中数学课程以学生发展为本,落实立德树人根本任务,培养和提高学生的数学核心素养.面向全体学生,实现人人都能获得良好的数学教育,不同的人在数学上得到不同的发展.通过高中数学课程的学习,提升学生作为现代社会公民所应具备的数学素养,促进学生自主、全面、可持续地发展.逐步学会用数学的眼光观察世界,发展数学抽象、直观想象素养;用数学的思维分析世界,发展逻辑推理、数学运算素养;用数学的语言表达世界,发展数学建模、数据分析素养.增强创新意识和数学应用能力.[1]“高中生的推理能力现状如何?是否达到课程标准的要求?不同学校的学生在推理能力方面是否存在差异?”等问题是我们重要研究的课题.
二、文献综述
我国的数学教育一直关注数学本身的逻辑性、严谨性,过分地注重演绎推理的作用.东北师范大学的闫莉丽对高中是的数学合情推理进行了调查研究,认为在新的课程改革的基础上要更加注重数学合情推理的内容.[2]南京师大的林静也对高中生的合情推理的能力作了调查研究,认为在推理能力方面,应该加大合情推理的内容,提高高中生合情推理的能力.[3]新加坡的数学课程目标中要培养学生“逻辑思考和对结论进行论证”、“证明和解释结果,学会逻辑清楚地表达数学的观点和解决数学问题的方法”.日本在初中三年级的要求是“提高对图形性质的预测和逻辑推理能力.”这些要求和我国改革之前颁布的教学大纲要求很接近.全美数学教师理事会著的《美国学校数学教育的原则和标准》提出“要想使社会成员具有数学思维能力和推理能力,并掌握有用的数学基础知识和基本技能,我们必须要有一系列高要求的标准”,推理与证明是其中的一条标准,它对从学前期至12年级的学生数学推理水平要求是“认识到推理和证明是数学的基础提出并探讨数学猜想发展和评价数学推理和证明选择和运用不同的推理和证明方法”.[4]
三、研究设计和过程
(一)研究对象及工具
本研究选取酒泉市两所中学H和L进行问卷测试.H校选取高二、高三年级文、理各一个班,152人,学校整体发展水平较高,文中称水平较高学校;L校也选取高二、高三年级文、理各一个班,160人,学校整体发展水平处于同类学校中间,文中称水平一般学校.共计发放测试卷312份,全部收回.样本中,男生150人,女生162人;高二152人,高三160人;文科172人,理科140人.
结合文献[4]自编了测试试题,共计十道题目,每题10分,共计100分,如表1所示.
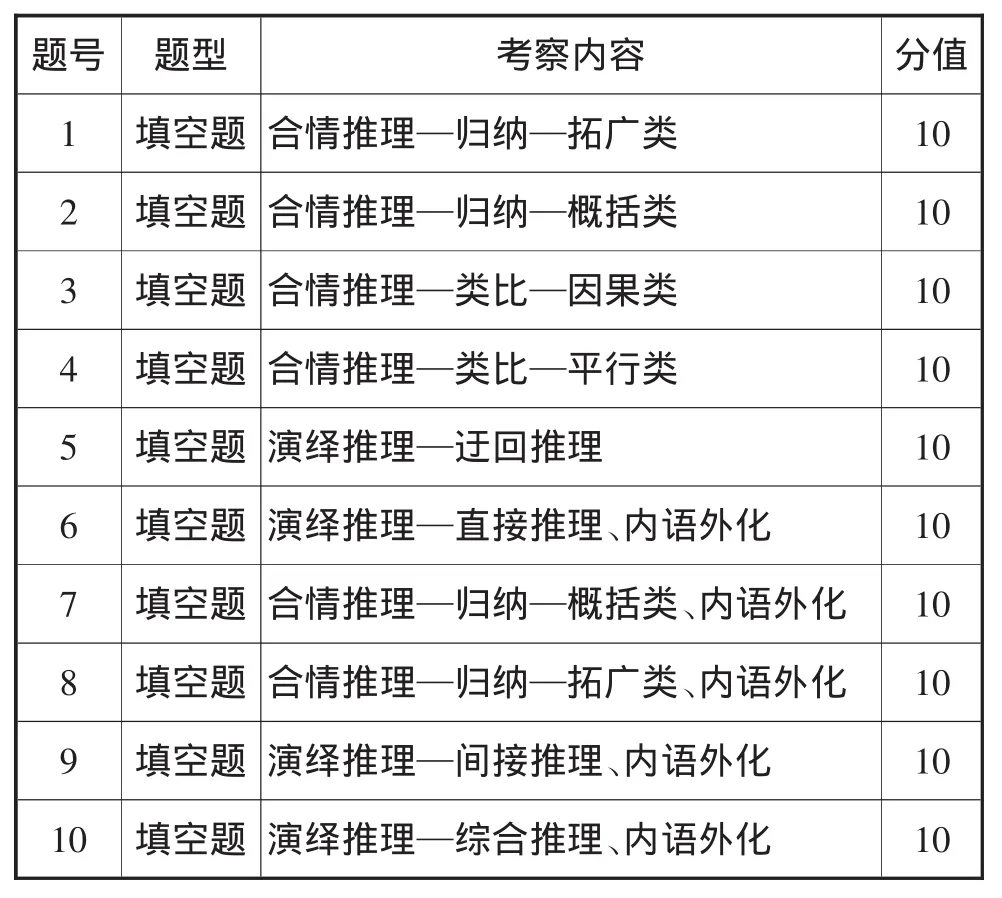
表1 推理能力的划分
(二)研究方法及程序
本研究主要采用了质性与量化的研究方法.质性的研究方法是结合文献以及高中生数学推理能力形成的重要性进行理性分析;量化的研究方法是在质性分析的基础上自编测试卷探寻高中生推理能力现状的差异性与关联性.核心是编制测试题,难点是测试成绩的确定.
本研究的程序包括三步,第一步是测试卷的编制、修订、试测、完善等过程.依据表1编制试测题,随机选取一个班级进行试测,根据试测的结果对试卷进行修订、完善.第二步是实施测试、打分,对所选择的样本进行测试、评分.第三步是数据统计分析.为了方便定量分析,对测试卷进行编码,H校共抽取152人,依测试卷按S01,S02,S03,…,S152进行编号(字母H代表学校,数字表示序号),L校也依此处理.将其测试的成绩数据按不同变量输入SPSS17.0汉化版中,采用描述统计对样本总体进行统计分析,采用独立样本T检验对各变量与高中生推理能力之间的差异性进行分析.[5]
四、调查结果与讨论
通过对所选研究对象的测试,经中学高级教师、研究者分别阅卷,两者成绩相同者即为确定分,不同者,经协商、研究确定分,根据得分情况,发现了如下3个结果.
(一)高中生推理能力的总体状况
首先研究312个样本同学测试成绩的总体情况,得到如下表2所示的结果.

表2 样本总体的数据统计表
由表2可知,样本的标准差为13.196,说明样本总体测试成绩比较稳定.平均成绩为71.24,极差为50分.若按60%及格率计算,及格以上(包含60分)的人数有235人,为总人数的75.32%.由于测试题是按课标要求编制的,说明有近80%的高中生推理能力已达到了课标要求.
其次,分不同类型学校研究高中生的推理能力现状,得到如下表3所示的结果.
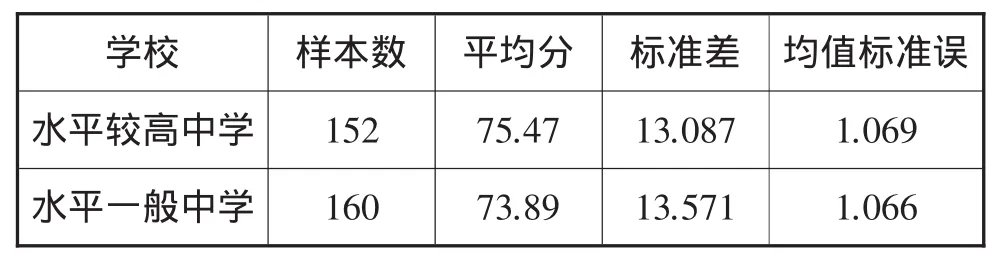
表3 水平较高中学与水平一般中学的数据统计表
由表3可知,水平较高中学学生的平均成绩比水平一般中学高1.58分,说明两类学校之间高中生的推理能力相差不大.水平一般中学的标准差比水平较高中学略大,说明水平较高中学的学生比水平一般中学的学生推理能力测试成绩较稳定.
再次,对两类学校学生的推理能力是否存在显著性差异进行了独立样本T检验.见表4.

表4 水平较高中学与水平一般中学独立样本T检验
由表4可知,通过方差齐性检验,发现p=0.488>0.05,说明两组样本方差差异不显著,采用第一行数据分析,t=1.044,p=0.297>0.05,表明水平较高中学与水平一般中学学生的推理能力测试成绩不存在显著性差异.反映出同一地区不同水平的学校虽然在总体的教学质量等方面有差别,但学生在推理能力方面不存在差异,学生的推理能力都获得了较好的发展.
(二)高中生推理能力与各变量间的相关性状况
推理能力涉及的相关因素较多,笔者仅从性别、年级、科别进行统计分析,得到如下结果.
1.高中生推理能力与性别的相关性
样本中男女生测试成绩平均分、标准差见表5,男女生独立样本T检验见表5.
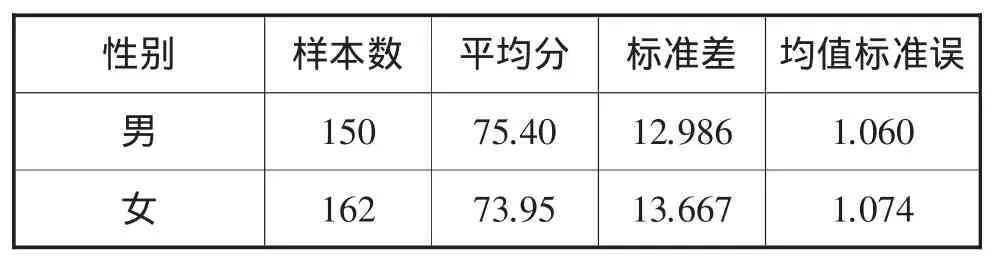
表5 样本全体男女生测试成绩平均分标准差
由表5发现,男生的平均分高于女士1.45分,标准差男生的略微低于女士,说明男生较女士发挥更加稳定.同时对全体男女生进行了独立样本T检验,得到表6,如下:
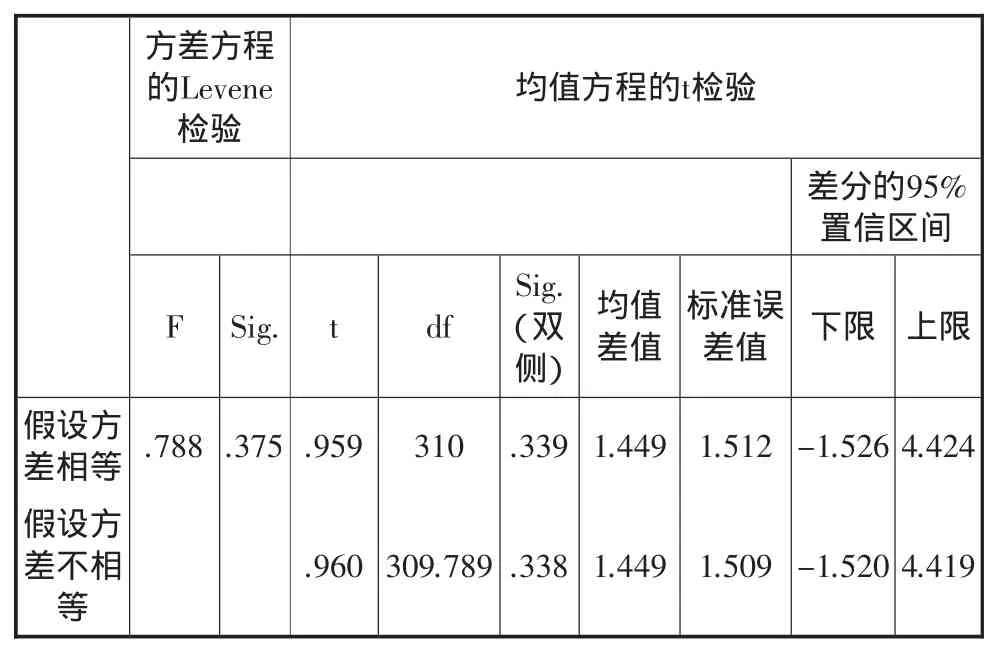
表6 样本全体男女生独立样本T检验
由表6可知,通过方差齐性检验,发现p=0.375>0.05,采用第一行数据分析,t=0.959,p=0.339>0.05,数据表明所调查的高中生推理能力不存在性别差异.
2.高中生推理能力与年级的相关性
是否随着年级的不同,学生在推理能力方面有差异,对此,分年级进行了统计分析,其高二、高三学生测试成绩平均分、标准差见表7,独立样本T检验见表8.

表7 样本全体高二、高三学生测试成绩平均分标准差

表8 样本全体学生的年级独立样本T检验
通过方差齐性检验,发现p=0.217>0.05,采用第一行数据分析,t=-0.988<0.05,数据表明所调查的高二、高三学生推理能力存在显著性差异,从平均分发现高三年级组比高二年级组高,说明随着年级的增长,学生的推理能力也在不断增强,从标准差发现,高三年级组的标准差要小于高二年级组,这说明高三年级组发挥更加稳定.
3.高中生推理能力与文、理科生的相关性
通常情况下,高中生在高二初进行文理科分班,不同科别高中生在推理能力方面是否有差异,对此,分不同科别进行统计分析,其结果见表9、表10.
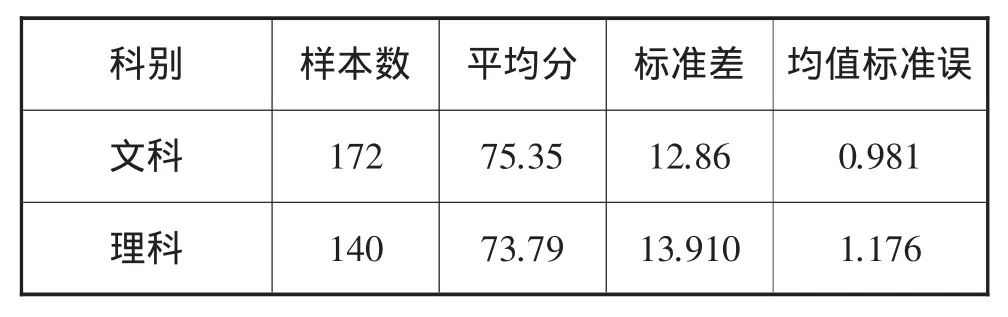
表9 样本全体文、理科学生测试成绩平均分标准差

表10 样本全体文、理科学生独立样本T检验
由表10可知,通过方差齐性检验,发现p=0.248> 0.05,采用第一行数据进行分析,t=1.029>0.05,数据表明高中生文理科推理能力不存在显著性差异.从平均分发现,文科生的平均分高于理科生的平均分,从方差发现,文科生的方差要小于理科生的方差,说明文科生在推理能力方面发挥更加稳定.
通过对测试数据的统计分析,得到关于高中生推理能力方面的如下研究结论:
一是大部分高中生的推理能力已达到了课标的要求;二是水平较高中学与水平一般中学学生的推理能力不存在显著性差异;三是高中生推理能力不存在性别差异;四是不同年级的高中学生推理能力存在显著性差异;五是文、理科学生推理能力不存在显著性差异;
五、研究结果对教学的启示
(一)在数学教学过程中自然融合推理能力的培养
学生推理能力的发展和提升与知识与技能的获取虽不对立,但决不是“一码事”知识与技能,只要学生“懂了”、“会了”、“熟练了”就可以获得,而学生能力形成是一个缓慢过程,甚至有迂回和曲折,它需要学生获取启示,“悟”出规律和思考方法,这种“悟”必须在长期的数学学习活动中才能达到.所以,作为教者要精心安排教学活动,创想、讨论、交流的空间和时间,让学生充分享受探索的“快乐”,激发学习潜能.在教学过程中,要让学生尽可能完整经历“观察、实验、猜想、归纳、验证”的推理活动过程,让学生主动探索,主动归纳.让推理能力培养自然融合于这样的过程之中.学生数学推理能力不能“传授”,更不等于“接受”,它是一个漫长的过程,而这个过程就是整个数学教学过程.
(二)培养学生推理能力,要循序渐进,体现“梯度”
学生数学推理能力培养是一个复杂过程,它需要不断“量”的积累.教学中,要有“耐性”,更需要长期“呵护”.就高中课程而言,数学推理主要包括合情推理和演绎推理两者既互相联系,又体现“梯度”.一般来说,合情推理培养相对容易,演绎推理能力要求较高.学生要获取数学结论,应当经历“合情推理——演绎推理”过程,这个过程就体现了由合情推理发展到演绎推理的“梯度”.因此,新课标对高中学段学生推理能力提出了更高的要求,新课程标准明确提出高中生的核心素养,其中数学运算推理是一大素养,要求高中生通过数学运算核心素养的培养,学生能够提高解决实际问题和数学问题的能力,提升逻辑推理的能力,形成程序化思考问题的习惯,养成实事求是、一丝不苟的科学精神.这中要求是前所未有的.
(三)在日常生活和学习中提高推理能力
新的高中课程标准中有三条内容主线:函数、代数与几何、统计与概率;把数学建模与数学探究、数学文化贯穿在课程中;这些知识点都和现实生活联系非常紧密,所以要在现实生活中培养学生的推理能力,特别是在平面几何和立体几何、数学模型等课程的学生中.这些课程为学生确定人生方向提供引导;为学生展示数学才能提供平台;
随着时代的发展,我们面临着更多的挑战,对高中生的能力要求更高,他们担负着社会的重担,希望他们能够在新的课程理念的指导下,掌握过硬的本领,开辟一片新天地.
1.数学课程标准研制组.普通高中数学课程标准(实验)解读[M].南京:江苏教育出版社,2004.
2.闫莉丽.高中生数学合情推理能力的调查研究[D].长春:东北师范大学,2012.5.
3.林静.高中生合情推理能力的调查研究[D].南京:南京师范大学,2014.5.
4.周静.初中生数学推理能力的调查研究[D].沈阳:沈阳师范大学,2011.5.
5.张定强,蒋会兵,王旭阳.高中生数据处理能力现状调查及教学启示[J].数学教育学报,2016,25(2).
