最优化视角下对数学线性规划内容的拓展
2017-06-10周如俊
周如俊


摘 要:从最优化视角对高中数学线性规划内容进行拓展,借助线性规划作图解决最值思想,从一个新的角度对高考有关线性(非线性)约束条件下线性(非线性)目标函数最值问题“模型构建”进行引申归类,形成“LC-LF”類、“LC-NLF”类、“NLC-LF”类、“NLC-NLF”类四种模型,并提出相应“破解”之策.
关键词:线性规划;拓展;高考题;类型分析
《全日制普通高中数学课程标准(实验)》中关于线性规划内容提到:线性规划是最优化的具体模型之一.在高中数学中,线性规划问题都是最简单的线性规划 (Linear Programming,简称LP) 问题,即线性约束条件下线性(目标)函数最优化问题.其数学思想在高考解题中具有很强的现实意义,核心是运用数形结合的思想方法,借助平面图形,求目标函数的最值问题[1].
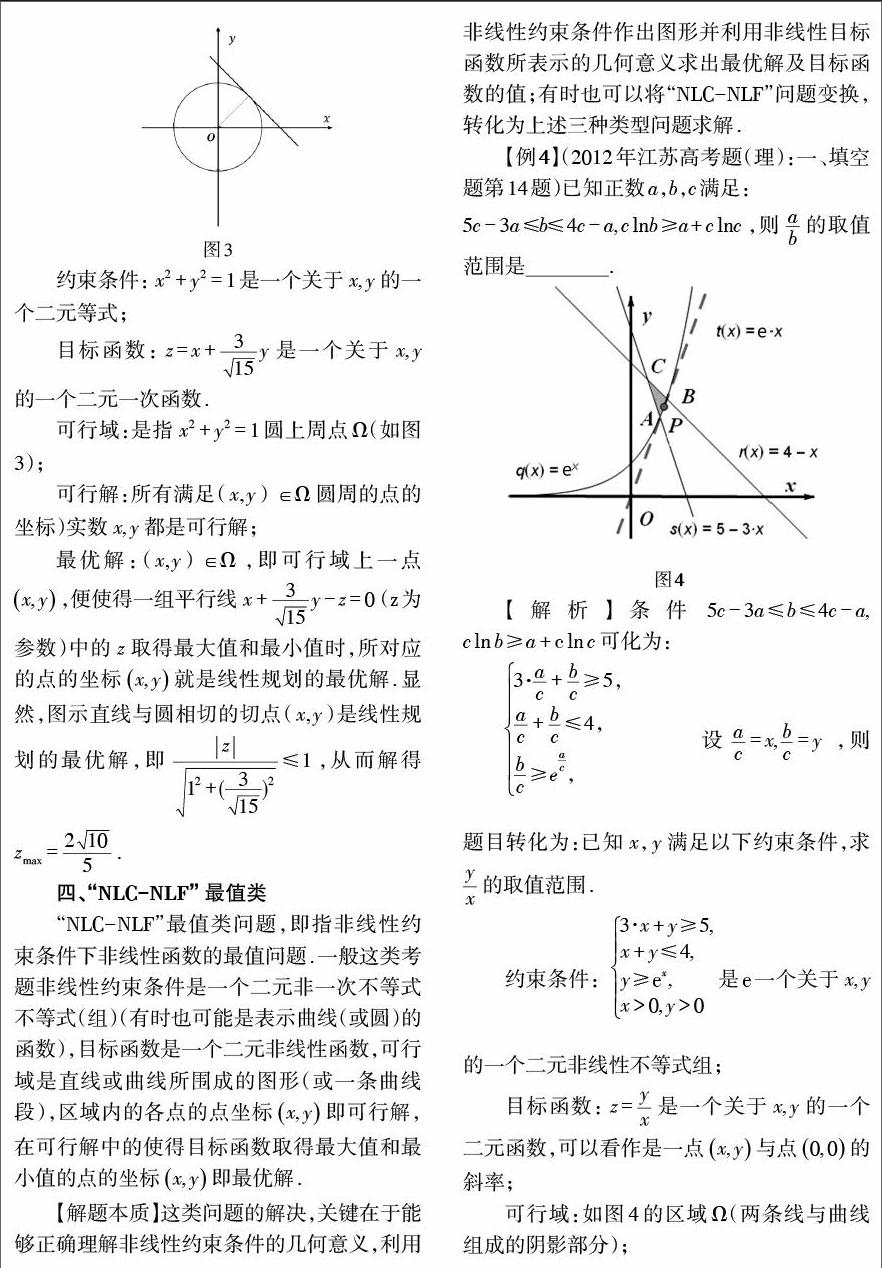
综观最近几年高考约束条件下目标函数最值考题,其内容都是对简单的线性规划问题的引申与深化.这涉及应用数学中最优化(Optimization)问题,其模型一般包括变量、约束条件和目标函数三要素.根据目标函数和约束条件性质,对最优化问题作进一步分类:当目标函数和约束条件都是线性的,则称线性规划;当目标函数或约束中有一非线性函数时,则称非线性规划;当目标函数是二次的,而约束是线性时,则称为二次规划.
笔者基于当前高考有关考题与命题趋势,从最优化视角对高考有关最值考题的约束条件与目标函数作表1所示分类,尝试对高中数学教材有关线性规划内容拓展.其中线性约束条件一般是指二元一次不等式组;非线性约束条件一般是指一个二元非一次不等式(组)(有时也可能是表示曲线或圆的函数);线性函数关系是指直线,而非线性函数关系是指非直线,包括各种曲线、折线、不连续的线等.适当对线性(非线性)约束条件下线性(非线性)目标函数问题“模型构建”,利用其函数的几何意义,借助作图解决高考最值问题,这是从一个新的角度对求最值问题的理解.
一、“LC - LF”最值类
“LC - LF”最值类问题,即指线性约束条件下线性函数的最值问题.一般这类考题线性约束条件是一个二元一次不等式组,目标函数是一个二元一次函数,可行域就是线性约束条件中不等式所对应的方程组所表示的直线所围成的区域,在可行域解中的使得目标函数取得最大值和最小值的点的坐标即简单线性规划的最优解.
【解题本质】这类考题的解决,重要在于能够正确理解线性约束条件所表示的几何意义,并画出其图形, 通过目标函数[z=ax+by(a≠0)]中直线[l:ax+by=0]的平移法,利用直线[y=-abx+zb]的纵截距[zb]解决最值问题(当[b]为正值时将直线[l:ax+by=0]向上平移使目标函数取得最大值,反之[b]为负值时向下移动使目标函数取得最小值);当线性目标直线的斜率与约束条件的边界相等时,最优解有无数多个.解题过程中关键是突破“画”(画出线性约束条件所表示的可行域)、 “移”(作平行直线)、“求”(解方程组求出最优解).这种求最值的方法也称“角点法”[2].
二、“LC-NLF” 最值类
参考文献:
[1]潘晓春.运用简单线性规划思想理解求最值问题[J].数学教学, 2006(4):25-27.
[2]张金龙,钱军先,李文斌.线性规划方法的本质:多元函数最值问题的图象解法[J].新高考:高三数学,2013(1):24-26,35.
[3]李剑.运用线性规划的思想解决多元变量求最值[J].数理化学习:高三版,2013(8):49-50.
[4]张琼.利用线性规划的思想求无理函数的最值[J].高中数理化,2011(17):20-21.
