复合纤维材料中压力传感器的应力分析和优化

唐 雯, 沈 斌

(同济大学 中德学院，上海 201804)

复合纤维材料中压力传感器的应力分析和优化

唐 雯, 沈 斌

(同济大学 中德学院，上海 201804)

在流量控制系统中，需要在由复合纤维材料制成的机翼中嵌入压力传感器。由于机翼结构会对压力传感器的性能产生影响，因此，通过有限元分析软件对该模型在一定拉力作用下的应力情况进行模拟，发现在压力传感器的边缘出现了应力集中。通过3种改进设计，可以降低或者消除应力集中，即对传感器的4个外直角进行倒棱操作；将传感器旋转45°后嵌入；在传感器外围黏合铝合金薄片。在对上述3种优化方法进行有限元分析模拟后，发现在传感器外围黏合铝合金薄片有效提高了传感器的抗拉强度，消除了应力集中。

复合纤维材料； 压力传感器； 应力集中； 有限元分析； 传感器设计优化

0 引 言

未来，飞机控制系统的重要性将进一步增加，因此研究中心SFB 88o目前正致力于研究流量控制系统。该项目的主要目标是研究一种新型的高升力装置，以提高飞机的上升高度及减少在起飞和降落过程中由于机翼振动而产生的噪声。其高升程利用康达效应实现，因此，在机翼端部会连接一个高度弯曲的翼片(康达翼)。为了避免空气流与康达翼分离，需要在翼片上施加一个加压空气射流，其流量大小的控制由可驱动的机翼边缘改变排气间隙大小实现。所需流量大小取决于飞机机翼上方气流的流动状态，该状态可以利用压力和热膜传感器来测量[1]。

目前，越来越多的飞机部件采用纤维复合材料，比如新空中巴士A350。在加工这种纤维复合材料的过程中，可以直接内嵌功能元件(如传感器)，从而制造一种智能复合结构。但是，这种封闭无极的结构也有其缺点，主要是纤维复合材料的结构对传感器施加的拉应力和扭矩对其性能造成了干扰。

本文对纤维复合材料中压力传感器进行了应力分析，并实验对比了3种优化方法消除应力集中的影响，发现通过对压力传感器添加金属薄片效果最好。

1 压力传感器工作原理

研究中心研发的压力传感器采用压阻效应,即电阻在压力或者拉力作用下电阻值发生了改变,改变由两部分构成，一部分是由材料自身的形变(长度和横截面积的改变)导致，一部分是由材料自身电阻率的改变导致。其比例关系如式(1)[2]

(1)

式中 v为泊松比；π为压阻系数；E为弹性模量。在半导体材料中，其电阻值改变主要由电阻率的改变引起，此时由于形变导致的电阻值变化可以忽略，其变化量主要取决于π和材料的E。

传感器横截面如图1所示，玻璃基座中央的空腔与上面覆盖的硅晶片构成了一个薄膜区域。当整个晶片上方受到压力或者拉力作用时，会在空腔对应的薄膜四周产生最大的拉应力或者压应力[3]。

图1 压力传感器截面图及拉力作用下的传感器

在图2所示a,b,c,d4个位置进行合理的压阻电阻布置。当薄膜受到压力作用时，纵向电阻在纵向上伸长，横向电阻在横向上伸长，由于压阻电阻纵向和横向上的压阻系数不同，所以纵向电阻和横向电阻的电阻变化不同，通过惠斯通电桥[4]即可根据电压变化测出传感器所受压力大小。

图2 压力传感器压阻电阻布置

2 有限元分析

为了研究当压力传感器嵌入复合纤维材料后传感器的受力情况，在ANSYS Workbench中导入一个简化的试件模型，模拟整个试件在拉伸实验中传感器的拉应力—应变情况。其具体结构如图3所示。

图3 试件模型结构

2.1 材料属性

在对该结构进行应力情况分析时，首先需要各组成材料的弹性属性，才能计算出一定拉力下的试件应力分布。

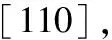
玻璃和纤维复合材料的参数见表1。

表1 玻璃和纤维复合材料参数

2.2 定义接触类型

在3维模型中，传感器的玻璃基座和硅晶片以及复合纤维材料制成的基体之间均互相独立，在有限元分析软件中被赋予不同的材料属性。在ANSYS中进行拉应力-应变分析时，需要根据实际情况定义不同材料的接触方式。实际制造时玻璃基座和硅晶片及传感器和复合纤维材料都是通过黏合剂组合在一起，所以，在有限元分析中默认接触方式为绑定(bonded)[7]。

2.3 定义约束类型

由于在拉伸实验中试件仅在一端受到拉力作用，并且只在拉力方向上有一个平移自由度，所以，在ANSYS中定义约束类型时，需要将试件的一个端面定义为固定约束(fixed support)，在另一个端面施加力，而其余4个面则定义为Displacement(给定位移)，并规定其只在受力方向上位移自由，其余方向位移受限。约束定义情况如图4。

图4 定义约束类型

3 结果分析

当对试件施加1 kN的拉力时，分析结果用最大主应力分布表示。根据文献[1]的实验结果，在拉力实验中，传感器的硅晶片最先被破坏，所以，图5中只显示了硅晶片的最大主应力分布。可以看出，硅晶片沿着拉力方向的两边应力值较大。为了更好探究硅晶片的应力分布，在显示分析结果时，可以只对硅晶片的两条中心线(x方向中心线和y方向中心线)进行分析，并根据拉应力值和其所在位置得出如图6所示的数据分布图。可以看出：晶片边缘0.1 mm的范围内，应力提高了大约80 MPa；在薄膜区域1.1～1.7 mm两个方向的应力很接近，说明该区域的应力分布较为均匀，两个方向的应力差对于传感器信号影响不大。由于存在应力集中，当硅晶片边缘的应力达到应力极限时硅晶片将发生断裂破损，所以需要对传感器采取必要的优化措施以降低硅晶片边缘上的应力，即清除应力集中提高了其承受拉力的能力。

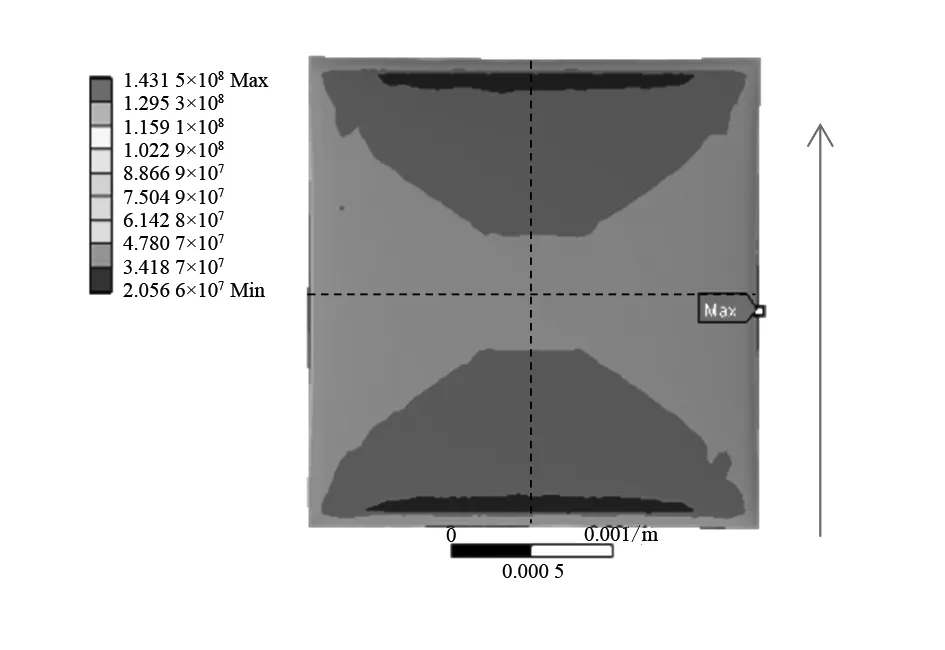
图5 硅晶片的最大主应力分布(拉力：1 kN)

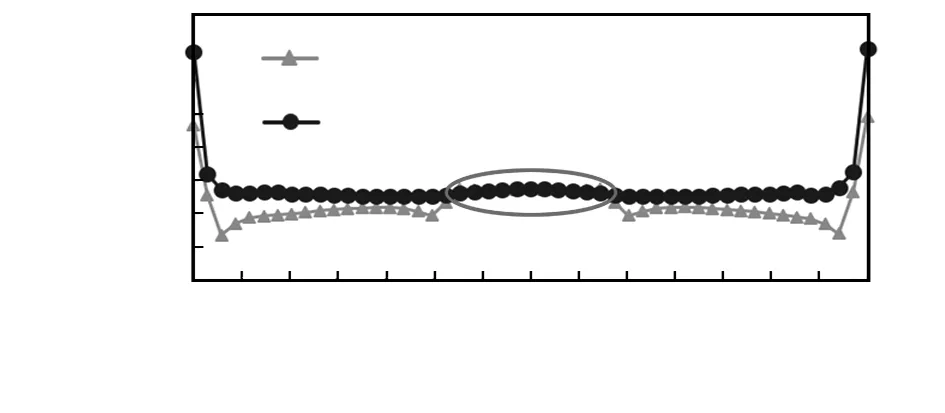
图6 硅晶片中心线应力分布

4 优化措施与结果

4.1 倒 棱

对传感器进行倒棱加工，即对传感器的4个外直角进行45°倒角，倒角尺寸为1 mm。模拟结果如图7所示。在1 kN的拉力作用下，硅晶片的最大拉应力有了一定降低，但是降低幅度并不明显，仅约20 MPa，并且根据沿其中心线的应力分布如图8所示，可以发现应力集中仍然存在。而在薄膜区域，应力值与倒棱前没有明显区别，说明倒棱操作对传感器测量信号性能的影响很小。

图7 倒棱后硅晶片最大主应力分布

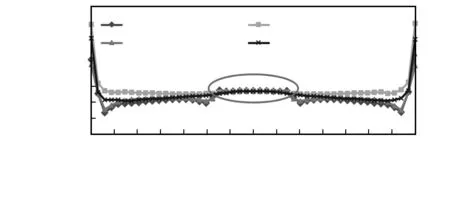
图8 硅晶片中心线应力分布(倒棱前和倒棱后)

4.2 旋 转

另一个比较简单的优化方法是在将传感器嵌入复合纤维材料时，将其绕中心旋转45°，如图9所示。在1kN的拉力作用下，最大拉应力值降低了大约30 MPa。根据模拟结果中最大拉应力出现的位置(近似为棱边的中点)，计算出经过该位置的中心线上的拉力值变化曲线，如图10所示，应力集中的情况仍然没有得到改善。

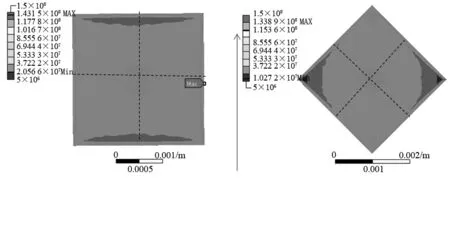
图9 旋转后硅晶片最大主应力分布

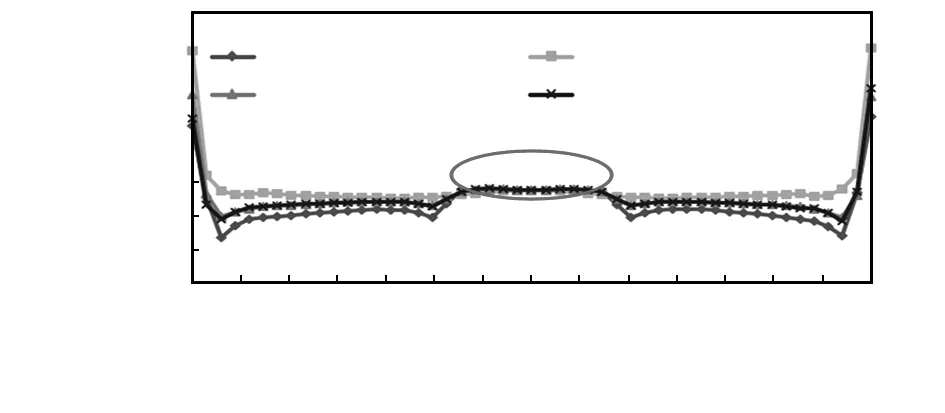
图10 硅晶片中心线应力分布(旋转前和旋转后)

4.3 增加金属薄片

因为通过在复合纤维材料中添加金属层可以提高复合纤维材料的抗拉强度[8]，所以,本文在传感器周围添加了一个与传感器同等厚度的金属薄片，假设它们可以紧密黏合，然后将黏合后的整体一起嵌入复合纤维材料。在有限元分析中设定采用的金属材料为铝合金，其密度为2 770 kg/m3，弹性模量为71 GPa，泊松比为0.33。

金属薄片的边长相对于传感器边长增加了0.4 mm，模拟结果如图11所示。添加金属薄片后硅晶片中的最大拉应力降低了大约60 %，其沿中心线的应力分布如图12所示，显示了在硅晶片边缘的应力集中已经被消除。根据图12，在添加金属后薄膜区域的应力有了一定的提高，但是总体仍然相对均匀。

图11 添加金属后硅晶片最大主应力分布

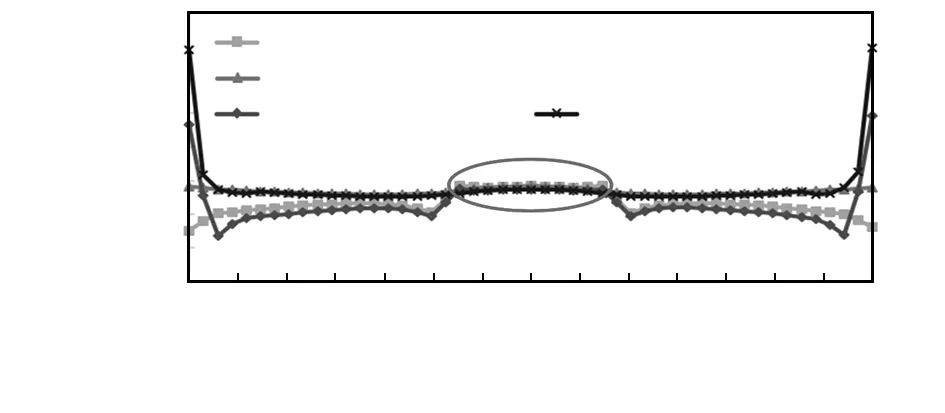
图12 硅晶片中心线应力分布(添加金属前和添加金属后)

虽然添加金属后传感器的最大拉应力值在同等情况下得到了降低，但是模型的最大拉应力值不再出现在传感器部分，而是在金属薄片边缘。表示随着拉力的增大，铝合金可能先达到应力极限，发生破损，从而影响传感器中的应力分布。

4.4 优化结果

采取上述的3种优化方法之后，整个模型的最大拉应力，硅晶片中的最大拉应力和薄膜区域中的最大拉应力如表2所示。

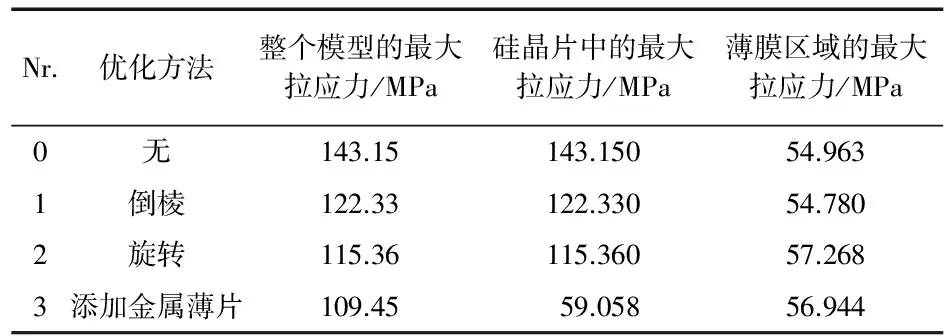
表2 优化结果

5 结 论

可以看出：薄膜区域的最大拉应力在各种优化方法下都没有太大变化，说明3种优化方法对传感器的测量信号性能影响都不大；添加金属薄片后，传感器的抗拉强度得到了显著提高，但是整个模型的最大拉应力并没有显著降低，该最大应力值出现在金属薄片边缘，而且几乎是硅晶片中最大拉应力值的2倍，说明当增大拉力时，金属薄片可能会最先到达应力极限，产生破损，并影响该优化方法的结果，这需要在以后的研究中加以注意。

在对整个模型进行有限元分析时，对模型进行了一定的简化，比如没有考虑玻璃基座中为黏合剂和导线留出的空位，导致模拟结果可能与实际结果会有一定偏差。并且在模拟中假定金属薄片和传感器是绑定连接，因此，在实际操作中还需要解决传感器与金属薄片黏合的问题，保证两者在拉力作用下不会彼此分离。

[1] Schwerter Martin,Leester-Schädel Monika,Stephanus Büttgenbach,et al.MEMS pressure sensors embedded into fiber composite airfoils[C]∥IEEE Sensors Proceedings,2014:531-534.

[2] 祝宇虹，纪军红，孙 宁.桥式硅压阻器件在气压测量中的应用[J].传感器技术,2005(5):74-76.

[3] 沈思国，丁建宁，潘海彬，等.纳米硅薄膜超微压力传感器设计与性能研究[J].传感器与微系统,2010,29(10):62-64.

[4] 时子青，陈向东，龚 静，等.一种新型MEMS温度传感器[J].传感器与微系统，2011,30(9):149-152.

[5] Hopcroft Matthew A,Nix William D,Kenny Thomas W.What is the Young’s modulus of silicon[J].Journal of Micro-electro-mechanical Systems,2010,19(2):229-238.

[6] Gräbner D.Integration und Einbettung eines Mikrosensors auf flexiblem Substrat[D].Braunschweig:IMT.2015.

[7] Christof Gebhardt.Praxisbuch FEM mit ANSYS Workbench[M].München: Carl Hanser Verlag.2014.

[8] Ebrahim Moussavi-Torshizi S,Dariushi S,Sadighi M,et al.A study on tensile properties of a novel fiber/metal laminates[J].Materials Science and Engineering:A,2010,527(18-19):4920-4925.

Stress analysis and optimization of embedded pressure sensor in composite fiber material

TANG Wen, SHEN Bin

(CDHK,Tongji University,Shanghai 201804,China)

In flow control system,pressure sensor is embedded in wing in material made of composite fiber of which the structure will affect performance of the pressure sensor.The stress situation of the embedded pressure sensor can be simulated with the help of finite-element-analysis software.The result is,that the stress concentration appears at the edge of the pressure sensor.By improving the design of sensor,the stress concentration can be reduced or eliminated.The improving methods include the chamfer of 4 right-angle corners of sensor,rotation of 45°before embedding,and a peripheral bonding with an aluminum foil.As a result of the finite-element-analysis simulation of these three improving methods,the bonding with aluminum foil effectively improves the tensile strength of the sensor and eliminates the stress concentration.

composite fiber material; pressure sensor; stress concentration; finite-element-analysis; optimization of sensor design

2016—07—23

10.13873/J.1000—9787(2017)06—0045—04

TP 212.2

B

1000—9787(2017)06—0045—04

唐 雯(1990-)，女，硕士研究生，主要研究方向为生产系统和过程技术。