新型电场传感器应用于输电线电场测量*

唐立军， 彭春荣， 顾植彬， 常亚东

(1．云南电网有限责任公司 电力科学研究院，云南 昆明 650217；2．中国科学院 电子学研究所 传感器技术国家重点实验室，北京 100190)

应用技术

新型电场传感器应用于输电线电场测量*

唐立军1， 彭春荣2， 顾植彬2， 常亚东1

(1．云南电网有限责任公司 电力科学研究院，云南 昆明 650217；2．中国科学院 电子学研究所 传感器技术国家重点实验室，北京 100190)

基于高性能的微电子机械系统(MEMS)工频电场传感器系统开展了高压架空输电线下电场测量应用研究。为了获得电场分布规律，基于模拟电荷法，建立了输电导线的二维电场计算通用模型。传感器系统核心敏感芯片基于电荷感应原理，采用MEMS技术加工制作。在0～1 000 kV/m工频电场范围内，传感器系统的总不确定度为1.53 %，分辨力达到了20 V/m。仿真与测试结果表明：35 kV与10 kV输电线下的电场计算结果与传感器系统的测量结果偏差分别为6 %和10 %，并与传统的Narda EFA—300电磁场分析仪测量结果具有较好的一致性。

电荷模拟法； 工频电场； 微电子机械系统； 电场传感器

0 引 言

高压输电线路地面电磁场强度是确定线路最小对地高度及规划线路走廊宽度的重要依据[1]。高压输电线路下的电磁环境受到越来越多的关注，特别是高压线下的电场强度，已成为环境保护和电磁兼容技术领域中不可忽视的问题[2]。

电磁场理论发展到现在，计算方法很多。常用的电磁场数值计算方法包括有限差分法、有限元法、边界元法以及模拟电荷法和模拟电流法[3,4]。有限差分法和有限元法二者都是对封闭的场域进行网格划分，不宜用来求解开域问题。边界元法虽然能够处理开域问题，但是边界元法的系数矩阵阶数比较高，而且是非对称的满阵，为线性方程组的求解带来困难。模拟电荷法和模拟电流法适合求解开域的静态场问题，在工程中有很广泛的应用。

经过多年的发展，目前常用的测量电场的方法主要有电容式电场传感器[5]、场磨式电场传感器以及光学式电场传感器等[6,7]。电容式电场传感器如德国Narda公司EFA—300体积大，空间分辨力低，价格昂贵；场磨式电场传感器主要用于直流电场测量；光学式电场传感器由于温度问题，目前主要还处于研究试验阶段。随着微电子机械系统(MEMS)技术的发展，国内外多家研究单位相继报道了多种MEMS微型电场传感器[8～15]。与传统的电场传感器相比较，MEMS电场传感器具有体积小、功耗低、成本低、易批量生产等优点。

为此，本文采用模拟电荷法对输电线路进行建模和场强计算，仿真计算35 kV输电线路三角形布置的电场分布随导线高度、线距变化规律，并采用高性能的MEMS工频电场传感器系统在输电线下进行现场测试。仿真与测试结果表明: 35 kV与10 kV输电线下电场计算结果与测量结果偏差不大于10 %，并与传统的Narda EFA—300电磁场分析仪测量结果具有较好的一致性。

1 输电线下场强基本理论与仿真

1.1 输电线路建模与场强计算

为了便于理论分析，对高压输电线路下场强计算问题做以下简化和处理：

1)输电导线是无限长光滑圆柱型导体，线径相同，彼此与大地间平行。

2)输电线半径r≪h(架设高度)，则高压输电线上的等效电荷可视为线电荷，其位置为输电导线的几何中心。

3)忽略输电线路杆塔、横担和弧垂的影响，将输电线视为无限长直平行导线，其产生的电场为二维场，如图1所示，计算平面取垂直于输电线最低点的垂面。

图1 高压输电线路计算模型

4)本文主要研究地面附近大约0～3 m高度内电场分布情况，在这个范围内，避雷线对电场分布的影响很小，忽略不计。

模拟电荷法采用镜像原理考虑大地对计算点P场强的影响，如图2所示。设大地为良导体，电位为零，带电量为Q的导线1与P点的距离为L，则导线1的镜像载有均匀电荷-Q，且与P点的距离为L′。

图2 等效电荷镜像原理

在已知电压等级情况下，求出各模拟电荷的电位系数，列出矩阵方程

(1)

式中P为n×n阶电位系数矩阵，Q为模拟电荷电量列向量，Q为输电线路电位列向量。由上式可得

Q=P-1U

(2)

求解得到等效电荷Q，则不同输电线路单位长度线电荷在空间某一点所引起的电场强度可以用叠加原理求得，表示为

(3)

式中 (x0,y0)为计算点P的坐标，(xi,yi)为输电导线i的坐标，m为输电导线数目，Qi为导线i的等效电荷(i=1,2,…,m),则在计算点处合成场强为

(4)

如果实际输电线路为分裂导线，则通常从整体上简化线路为圆柱导线，那么导线的截面为圆，其等效半径Ri的计算公式如下

(5)式中R为分裂导线半径；n为次导线根数；r为次导线半径。

1.2 输电线路电场仿真

在研究分析架空输电线路电场强度计算原理的基础上，可以得到输电线路场强大小与输电线路布置方式、高度、距离等因素之间的关系。本文以35 kV输电线路为例，对不同的高度、线间距离分析线下电场强度变化情况。采用如图3所示的单回3相输电线路模型，H1,H2分别为导线高度，D1,D2为线路之间水平方向距离。

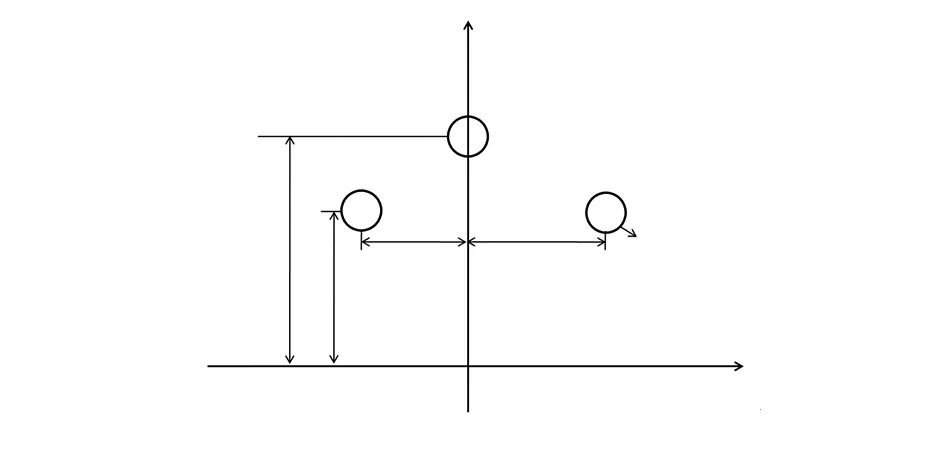
图3 单回3相输电线路

采用Matlab软件进行仿真分析，图4 为线下合成电场仿真计算结果。由图4可发现：随着两水平导线之间距离减小，线下的合成电场值减小，合成电场分布由“马鞍形”逐渐变成“钟形”；随着三角顶点处导线与两水平导线之间距离减小，合成电场值减小，合成电场分布中心点处的电场值减小幅度增大；随着导线离地距离减小，电场值增大。

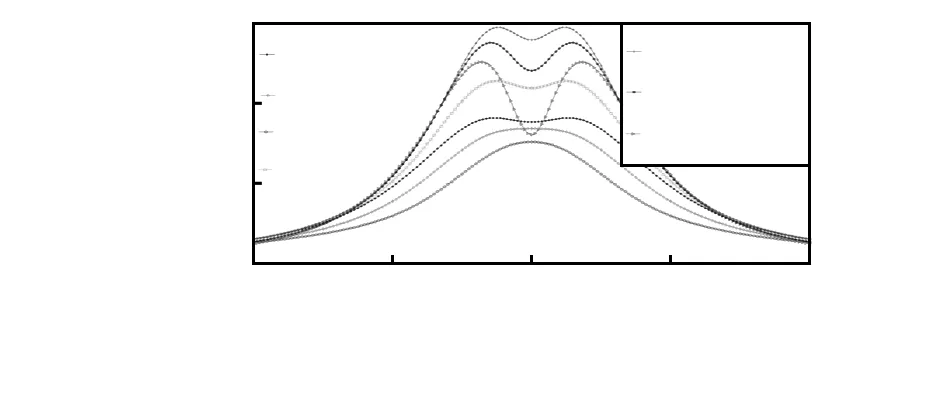
图4 35 kV输电线路上三角布置电场仿真结果

在上述输电线下电场强度计算仿真的基础上，开展基于MEMS敏感芯片的工频电场测试系统的线下电场测量应用研究。

2 基于MEMS敏感芯片的工频电场测试系统

MEMS电场敏感芯片是中国科学院电子学研究所研制的创新产品，其感应原理如图5所示[15]。在芯片正上方施加电场En，当屏蔽电极在感应电极(+)和感应电极(-)之间周期性水平左右振动时，调节感应电极周围电场发生变化，引起其表面的感应电荷量发生周期性改变，产生与被测电场成正比的交变感应电流，经过I/V转换后输出交变电压，通过测量交变电压计算出被测电场大小。

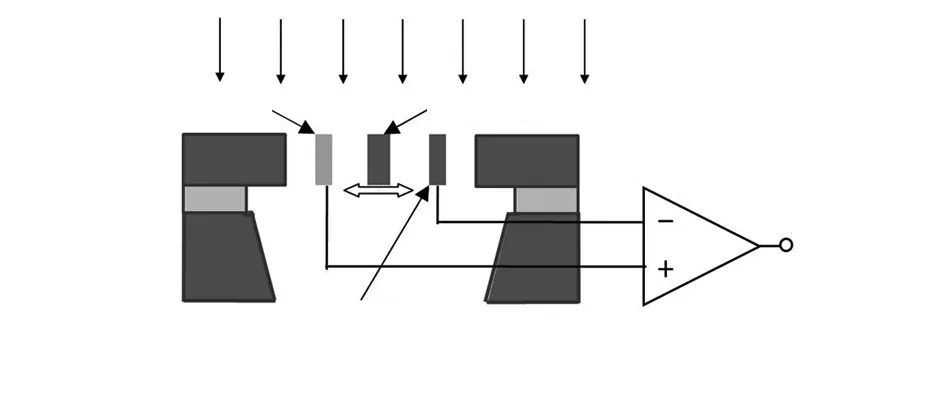
图5 MEMS电场敏感芯片感应原理

基于MEMS敏感芯片的工频电场测试系统主要包括传感器探头(MEMS电场敏感芯片，前置放大电路),驱动电路,NI无线信号采集卡、电源模块以及上位机等。MEMS电场传感器探头如图6所示。NI无线信号采集卡将探头的输出信号和驱动电路的激励信号采集后以无线方式发送到上位机进行信号解调。数据无线传输保证了MEMS电场传感器探头与地隔离，测量不受地电势的影响，提高了测量的准确性，也提高了系统的安全性。

图6 MEMS电场传感器探头

在0～1 000kV/m电场范围内，MEMS工频电场测试系统线性良好，其总不确定度为1.53 %，分辨力达到了20V/m。

3 仿真与测试结果对比

采用文中的输电线路电场仿真方法和MEMS工频电场测试系统分别对35,10kV输电线路的电场分布进行仿真计算和测试，主要仿真测试输电线路正投影下水平面上与输电线路垂直方向±10m范围内的电场分布，仿真测试离地高度1.8m。另外，仿真测试结果与Narda公司的EFA—300电磁场分析仪的测试结果进行对比。

由于实验选择的35kV输电线路为上字塔不对称三角形布置方式，所以，在输电线路两侧进行电场测试。图7(a)为35kV输电线下电场分布计算与测试结果。MEMS工频电场测试系统除了在+2m处有一个较大的抖动外，其他测试点均与理论模拟结果以及NardaEFA—300的测试结果相一致，测量最大偏差为6 %，测试结果也真实地反映了线下两侧电场不对称情况。

图7 输电线路计算与测试结果

由于10kV输电线路呈上三角形布置，左右对称，所以,只仿真测量其右侧的电场分布情况。图7(b)为10kV输电线下电场分布仿真与测试结果。仿真结果与测试结果也具有较好的一致性，在测试区间内，MEMS工频电场测试系统的最大偏差约为10%，曲线趋势和大小真实反映出了输电线下电场分布特征。

4 结 论

本文首先基于模拟电荷法建立了输电线下的电场分布计算模型，并仿真计算了35kV输电线路在不同的高度、线间距离条件下电场的分布规律。然后介绍了高性能MEMS工频电场测试系统，在0～1 000kV/m电场范围内，系统线性良好，总不确定度为1.53 %，分辨力达到了20V/m。仿真与测试结果表明：35kV与10kV输电线下的电场计算结果与系统的测试结果的偏差分别为6 %和10 %，并与传统的NardaEFA—300的测试结果一致性良好，说明高性能的MEMS工频电场测试系统可用于输电线下的电磁环境测量。

[1] 罗 杰,黄小庆,何 杰,等.输电线路在线监测WSNs优化部署研究[J].传感器与微系统,2014,33(8):52-55,64.

[2] 胡顺仁,曾 锋,赵 红,等.特高压输电塔实时监测系统的数据传输方法研究[J].传感器与微系统,2012,31(9):42-45.

[3] 孟 毓,张永隆,肖鑫鑫.上海地区典型220 kV架空线线下场强的研究[J].电网技术，2010，34(6):38-43.

[4] 陈 楠,文习山,刘 波,等.高压输电导线三维工频电磁场计算与测量[J].电网技术，2011，35(3):160-164.

[5] 姚 境,汪 沨,胡 凯,等.传感器在高压输电线路绝缘子检测中的应用[J].传感器与微系统,2010,29(10):1-3,8.

[6] 汪金刚,林 伟,李 健,等.电容式交变电场传感器与工频电场检测试验研究[J].传感器与微系统,2010,29(9):21-23,26.

[7] 方奕庚,彭春荣,方东明,等.微型折叠式三维电场传感器[J].传感器与微系统,2016,35(5):1-4.

[8] 席 洁,陈 明,弟 寅,等.测量电场的铌酸锂光传感器综述[J].传感器与微系统,2013,32(3):4-6,14.

[9] 王 宇,方东明,陈 博,等.基于旋转谐振结构的单芯片二维电场传感器[J].传感器与微系统,2016,35(2):103-105,112.

[10] Bahreyni B,Wijeweera G,Shafai C,et al.Analysis and design of a micromachined electric field sensor[J].Journal of Micro-electro-mechanical Systems,2008,17(1):31-36.

[11] 陈中伟,肖 华,吴功平.高压巡线机器人电磁传感器导航方法[J].传感器与微系统,2006,25(9):33-35,39.

[12] Peng Chunrong,Chen Xianxiang,Bai Qiang,et al.A novel high performance micromechanical resonant electrostatic field sensor used in atmospheric electric field detection[C]∥Proc of 19th IEEE Conf on MEMS,Istanbul,Turkey,2006:698-701.

[13] 闻小龙,彭春荣,方东明,等.基于共面去耦结构的空间三维电场测量方法[J].电子与信息学报,2014,36(10):2504-2508.

[14] 杨鹏飞,彭春荣,张海岩,等.SOI微型电场传感器的设计与测试[J].电子与信息学报,2011,33(11):2771-2774.

[15] Yang Pengfei,Peng Chunrong,Zhang Haiyan,et al.Design and testing of a SOI electric-field microsensor[J].Jounal of Electro-nics & Information Technology,2011,33(11):2771-2774.

[16] 封滟彦,俞集辉.超高压架空输电线的工频电场及其影响(一)[J].重庆大学学报，2004，27(4):10-14.

唐立军 (1985-)，男，工学硕士，工程师，主要从事电网自动化检测及测试技术、多源信息融合技术方面的研究工作，E—mail：tlijun@foxmail.com。

New type of electric field sensor for electric field measurement of transmission line*

TANG Li-jun1, PENG Chun-rong2, GU Zhi-bin2, CHANG Ya-dong1

(1.Electric Power Research Institute,Yunnan Power Grid Co Ltd,Kunming 650217,China；2.State Key Laboratory of Transducer Technology,Institute of Electronics,Chinese Academy of Sciences,Beijing 100190,China)

Electric field measurement under high voltage overhead transmission using a high-performance MEMS electric field sensor is presented.To study the distribution of electric field under high voltage overhead transmission lines,based on the charge simulation method,a generic model for two-dimensional electric field calculation is established.To measure the electric field distribution,a novel measurement system of wireless transmission based on high-performance MEMS electric field sensing chips is introduced.Tested in ambient air conditions,the minimum detectable field of the system is approximately 20 V/m,with an uncertainty of 1.53 % in working frequency electric field range 0～1 000 kV/m.The simulation and test results show that the deviation between the calculation results and the test results of the system for electric field under 35 kV and 10 kV transmission lines is 6 % and 10 %,respectively,and the plotted curves of the system are consistent with traditional Narda EFA—300 electromagnetic field analyzer.

charge simulation method(CSM); power frequency electric field; micro-electro-mechanical system (MEMS); electric field sensor

2016—06—21

国家“863”计划资助项目(2015AA042602)；中国南方电网有限责任公司科研项目(K—YN2014—186,YNKJXM00000293)

10.13873/J.1000—9787(2017)06—0154—03

TM 937

A

1000—9787(2017)06—0154—03