分段变步长MPPT算法在风力发电系统中的应用*

赵 甲， 李文磊， 杨鹏龙

(宁波大学 信息科学与工程学院，浙江 宁波 315211)

分段变步长MPPT算法在风力发电系统中的应用*

赵 甲， 李文磊， 杨鹏龙

(宁波大学 信息科学与工程学院，浙江 宁波 315211)

针对传统定步长爬山搜索(HCS)法在风力发电系统最大功率跟踪(MPPT)控制过程中的快速性和准确性矛盾，提出了一种基于爬山搜索法和模糊控制的分段变步长MPPT算法。该算法根据发电机P-ω特性曲线对最大功率点(MPP)跟踪过程进行分段，使系统能够根据工作点所在的区域选择合适的跟踪算法和步长完成最大功率跟踪。在Matlab/Simulink中分别对提出的模糊分段变步长算法和传统爬山搜索法进行了仿真。仿真结果表明：所提算法明显地改善了系统跟踪MPP的速度和稳态精度，在MPPT方面明显优于传统的爬山搜索法。

风力发电； 最大功率跟踪； 分段变步长；P-ω特性曲线

0 引 言

风力发电系统可以将自然界中的风能转换为供生产生活使用的电能，然而在不同的风速下，风电系统存在一个最佳功率点，使系统输出功率达到最大。为了提高风力发电系统的发电效率，有必要对风电系统进行最大功率跟踪(maximum power point tracking ,MPPT)控制,保证其尽可能地工作在最大功率点(maximum power point,MPP)上[1]。

目前，常用的MPPT控制算法有：功率信号反馈法、叶尖速比法、爬山搜索 (hill-climbing searching,HCS) 法等。爬山搜索法与前两种控制策略相比，因不需测风装置和预先测量系统最佳功率曲线而得到广泛应用。但传统的爬山搜索法由于搜索步长固定，存在动态跟踪速度快和稳态跟踪准确度高的矛盾，限制了跟踪效率。针对此不足，文献[2]提出了基于三点比较的变步长最大功率跟踪策略，但系统跟踪到MPP附近后仍存在振荡[3]。文献[4]通过估测初始叶尖速比值，以缩小MPP的跟踪范围，但初始叶尖速比值的估测存在一定的误差。文献[5]利用指数衰减步长抑制系统在MPP附近振荡，但系统稳态精度受衰减因子影响较大。文献[6]将模糊控制应用到MPPT中，改善了传统爬山法的振荡问题，但降低了动态响应速度。

所有针对爬山法的改进策略旨在寻找合适的步长以提高跟踪MPP的快速性和精确性。本文提出了模糊分段变步长MPPT算法，使系统根据当前工作点的位置选择合适的跟踪算法和扰动步长。当系统工作点距离MPP处较远时选择步长较大的爬山搜索法以快速地跟踪到MPP，反之,则选择模糊控制策略[7]，使其稳定在MPP处运行。最后在Matlab/Simulik环境中进行了对比仿真验证，结果表明:所提方法能有效地改善系统在MPPT控制时的速度及稳态输出精度。

1 风力机输出特性

风力机将通过桨叶的风能转换为机械能以带动发电机转动，因此，风力机的输出功率决定了整个风电系统输出电能的大小。根据贝兹理论和空气动力学原理，其输出的机械功率可以表示为

(1)

式中ρ为空气密度，kg/m3；Rtur为风力机风轮半径，m；Cp为风能利用系数；υ为风速，m/s。

由式(1)可知，风力机输出的机械功率由风速v和风能利用系数Cp决定，某一风速下，输出功率随Cp变化而变化。风能利用系数Cp可以表示为

(2)

式中 β为风轮桨距角，(°)；λ为叶尖速比。

风力机的叶尖线速度与风速之比为

(3)

式中 ωtur为风力机的角速度，rad/s；ntur为风力机的转速，r/min。

由式(2)可知，当系统运行在额定功率以下时，叶片桨距角β不变，风能利用系数Cp只与叶尖速比λ有关。根据式(3)，此时存在一个最佳转速ωopt使风力机获得最佳叶尖速比λopt，同时，风能利用系数达到最大值Cpmax。

图1为不同风速下，风力机的输出功率和转速的关系曲线。任一风速下，风力机输出的机械功率由转速决定，且存在一个最佳转速ωopt使得风力机输出功率达到最大，所有的最大功率点组成了风力机最佳功率曲线Ptur_opt。

图1 风力机Ptur- ω关系曲线

综上可知，风力发电系统MPPT控制,即当风速改变时，通过调节风力机转速，使系统工作点尽可能地在最佳功率曲线上，提高系统的风能捕获率和发电量。

2 传统爬山搜索法

传统爬山搜索法根据风力机Ptur-ω关系曲线的单极点特性，当周期性地施加给风力机一个固定的转速扰动时，通过测定扰动引起的风力机输出机械功率的变化方向，确定下一次扰动施加方向。重复此过程，最终使系统工作点逐渐逼近MPP，如图2所示。

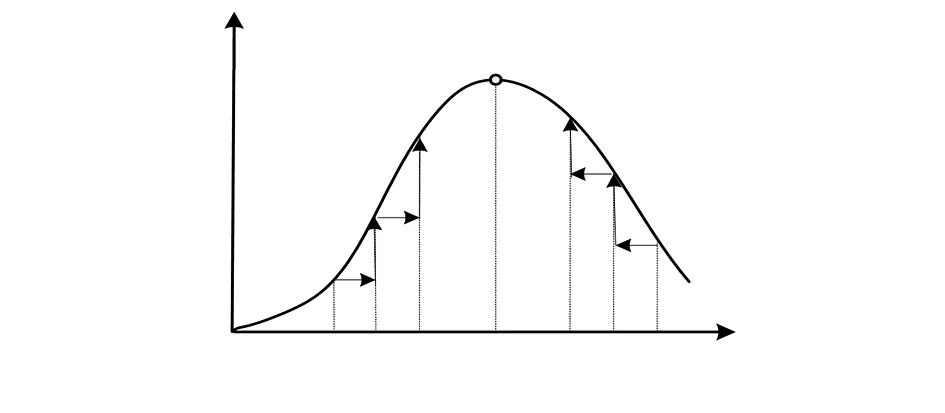
图2 爬山搜索法跟踪MPP过程

图2所示上山阶段中，ω，P分别为前一时刻风力机转速及其对应的输出功率，当正向施加转速扰动Δω，即ω1=ω+Δω，若P1P，说明此时系统工作点在MPP右侧，即如图2下山阶段，应反向减小转速，即ω1=ω-Δω，使工作点靠近MPP，如此反复，直至到达MPP附近。

因传统爬山法扰动步长固定，当选择较大的跟踪步长时，系统输出功率最终会在MPP附近来回振荡，稳态精度低；当选择较小的跟踪步长时，又很难快速地跟踪到MPP处，做不到快速性和精确性的统一。为此，本文提出了模糊分段变步长MPPT算法。

3 模糊分段变步长MPPT算法

3.1 算法原理与结构

在直驱永磁同步风力发电系统中，因风力机和永磁发电机转速相同，通过对发电机转速控制即可实现系统MPPT控制。模糊分段变步长MPPT算法原理为：根据风力发电系统P-ω曲线的单峰值特性，利用二次微分值的正负将MPPT过程划分不同的区域，如图3所示。

图3 模糊分段变步算法的跟踪区域划分

当功率对转速的二次微分满足d2P/dω2≥0时，说明系统工作点在离MPP较远的区域1和区域2中，则选择较大步长的爬山法加快系统跟踪至MPP附近的速度；当d2P/dω2≤0时，说明系统工作点在离MPP较近的区域3中，则选择模糊控制以保证在MPP处的精确跟踪。

风力发电系统模糊分段变步长MPPT算法中的模糊控制器包括模糊化、知识库、逻辑判断、反模糊化4个部分[9]。模糊控制器输入量为当前时刻发电机的输出功率变化量ΔP(k)和转速扰动步长Δω(k)，输出量为下一时刻的转速扰动步长Δω(k+1)。

3.2 模糊控制器设计

根据模糊控制器的设计过程，采用量化因子将功率变化量ΔP和转速扰动步长Δω的实际值模糊化，将其分别映射至模糊集合论域EP和Eω。定义模糊集合论域EP和Eω分别包含8个和6个模糊子集，表示如下

(4)

各模糊子集定义为NB(负大)，NM(负中)，NS(负小)，NO(负零)，PO(正零)，PS(正小)，PM(正中)，PB(正大)。将模糊集合论域EP和Eω离散化，表示如下

(5)

根据图1所示的风力发电系统P-ω特性曲线，可得在模糊控制下系统跟踪MPP的逻辑规则：

1)当对发电机施加转速扰动后，若ΔP(k)>0，说明系统工作点正靠近MPP，则继续向原扰动方向增加扰动，即ω(k+1)=ω(k)+Δω(k+1)；反之，说明系统工作点正远离MPP，则应反向增加扰动，即ω(k+1)=ω(k)-Δω(k+1)。

2)系统根据当前工作点到MPP的距离，能自适应地改变跟踪步长，提高跟踪速度和稳态精度。

3)当风速突变引起发电机输出功率发生较大变化时，系统能及时选择合适的控制算法和跟踪步长，对风速突变做出迅速的响应。

4)若ΔP(k)=0，则表明系统工作在最大功率输出状态。

根据以上MPPT原则，将三角形函数作为各模糊量的隶属度函数，选择ifAandBthenC作为模糊控制规则，得到MPPT模糊控制规则表,如表1所示。

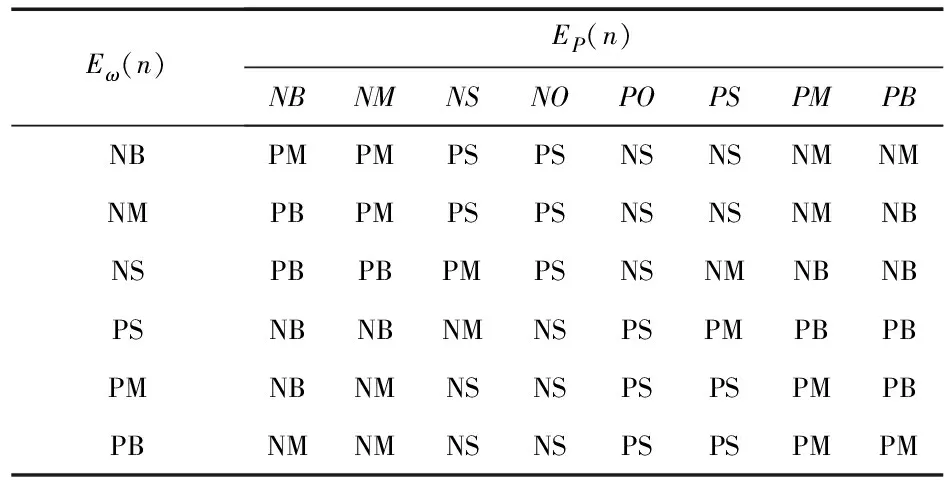
表1 MPPT模糊控制规则表

将模糊量输入所设计的模糊控制器，得到输入输出关系曲线如图4所示。

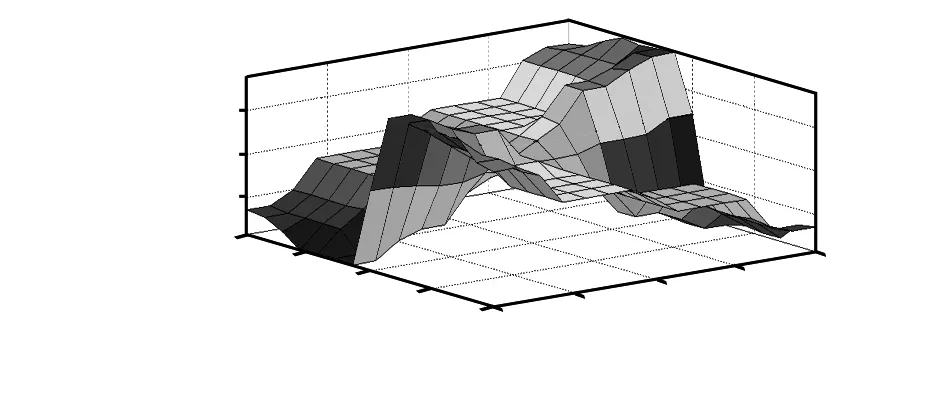
图4 模糊控制器输入—输出曲线

4 仿真研究

在Matlab/Simulink环境中建立了直驱永磁同步风力发电系统仿真模型，如图5所示。图中机侧功率变换器为电压型三相脉宽调制(PWM)整流器，采用空间矢量脉宽调制(SVPWM)；子系统模块为机侧功率变换器控制单元开关模块实现爬山搜索法和模糊控制之间的转换。模型参数如下：风力机风轮半径为4.5 m；桨距角为0°；空气密度为1.225 kg/m3，永磁同步发电机极对数为30;定子d,q轴电感均为1.08 mH;转动惯量为2.7 kg/m2。

图5 直驱永磁同步风力发电系统结构

设定在1 s时刻风速从初始风速6 m/s突变至10 m/s，分别采用模糊分段变步长算法和爬山搜索法进行MPPT仿真，结果如图6。

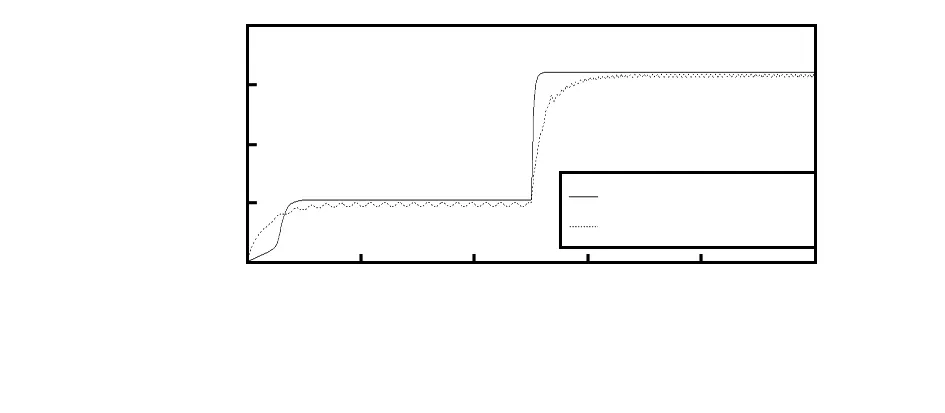
图6 风力发电机转速

由图6可知，初始风速下，采用模糊分段变步长算法时，系统在0.2 s时发电机转速即达到最佳转速，并稳定在10.5 rad/s；采用爬山法时，发电机机稳态转速会在9.5 rad/s上下波动。在1 s时风速突变，采用模糊分段变步长算法时，系统在0.1 s内恢复稳态，转速稳定在32 rad/s，跟踪速度和稳态精度优于爬山法。

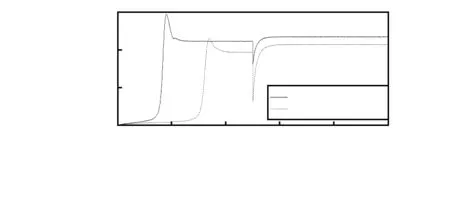
图7 风能利用系数

由图7可知，采用模糊分段变步长算法时，稳态时风力发电系统的风能利用系数明显高于爬山法，且不会出现爬山法在1 s时刻出现的严重跌落现象，说明所提算法能有效地提高风能利用率。

由图8可知，当风速突变时，采用所提算法，系统在1.1 s时功率达到最大值，稳态时稳定在1 820 W附近，较爬山法有所提高；而采用爬山法时，系统在1.15 s时到达稳态，且稳态输出功率在1 750 W附近有明显波动。

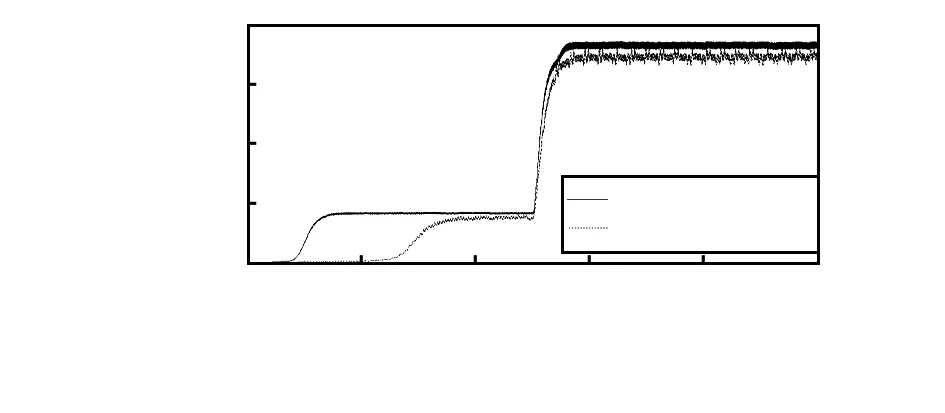
图8 发电机输出功率

5 结 论

本文针对传统爬山搜索法在最大功率跟踪过程中的快速性和精确性矛盾，提出了模糊分段变步长MPPT控制算法，并基于直驱永磁风力发电系统对其仿真验证。仿真对比分析表明：当风速变化时,算法既能快速地使系统跟踪到MPP又能稳定在其上运行，有效地改善了MPPT速度和精度，合理地提高了风能利用率。

[1] 吴政球,干 磊,曾 议,等.风力发电最大风能追踪综述[J].电力系统及其自动化学报,2009,21(4):88-93.

[2] 黄守道,佘 峰,黄科元,等.三点比较法在风力发电系统中的应用[J].控制工程,2009,16(6):764-767.

[3] Zhao R D,Wang Y J,Zhang J S.Maximum power point tracking control of the wind energy generation system with direct-driven permanent magnet synchronous generators[C]∥Proceedings of the CSEE,2009:106-111.

[4] 田 兵,赵 克,孙东阳,等.改进型变步长最大功率跟踪算法在风力发电系统中的应用[J].电工技术学报,2016,31(6):226-233.

[5] 陈毅东,杨育林,王立乔.一种新型变步长MPPT控制在风电并网系统中的运用[J].太阳能学报,2012,33(3):462-467.

[6] 张秀玲,谭光忠,张少宇,等.采用模糊推理最优梯度法的风力发电系统最大功率点跟踪研究[J].中国电机工程学报,2011,31(2):119-123.

[7] 董 静,王君君,陈天恩.前向模糊推理的菇房异常环境预警系统[J].传感器与微系统,2016,35(9):85-88.

[8] Hong C M,Chen C H,Tu C S.Maximum power point tracking-based control algorithm for PMSG wind generation system without mechanical sensors[J].Energy Conversion & Management,2013,69(69):58-67.

[9] 袁传义,刘成晔,贝绍轶.车辆主动悬架模糊自适应控制与试验研究[J].传感器与微系统,2010,29(8):15-18.

Application of variable step size MPPT algorithm in wind power generation system*

ZHAO Jia， LI Wen-lei， YANG Peng-long

(Faculty of Information Science and Engineering,Ningbo University,Ningbo 315211,China)

To avoid the contradiction between the rapidity and the accuracy of the traditional fixed step size hill-climbing search(HCS) method in the maximum power point tracking(MPPT)control of wind power generation system,a variable step size MPPT control algorithm based on the hill-climbing method and the fuzzy control method is proposed.In this algorithm,the maximum power point(MPP) tracking process is segmented according to theP-ωcharacteristic curve of generator and the system can select the appropriate tracking algorithm and the step size to achieve MPPT,when the system operates in different regions.The proposed algorithm and the traditional hill-climbing method are simulated respectively by Matlab/Simulink software.The simulation results verify the proposed algorithm can significantly improve the tracking speed and steady-state precision.Therefore,this method is better than the traditional MPPT search method.

wind power generation; maximum power point tracking(MPPT); variable step size;P-ωcharacteristic curve

2017—04—14

浙江省重中之重学科开放基金资助项目(XKXL1528)

10.13873/J.1000—9787(2017)06—0157—04

TP 13

A

1000—9787(2017)06—0157—04

赵 甲(1991-)，男， 硕士，研究方向为新能源发电， E—mail:zhaojia0107@163.com。

李文磊(1970-)，男，通讯作者，教授, 从事电力系统稳定性控制研究工作，E—mail:liwenlei@nbu.edu.cn。