大型风电机组轮毂静强度有限元计算方法研究

2017-06-09李静松邱俊李文军

农业科技与装备 2017年1期

李静松+邱俊+李文军

摘要：针对大型风电机组轮毂静强度有限元计算问题，提出“主轴-轮毂-轴承-叶片”整体等效模型，以及轮毂物理模型边界条件等效方法。介绍等效模型建立的过程及方法，通过相关计算验证边界条件等效的正确性。某2 MW风电机组轮毂静强度计算结果表明，计算方法用时减少，计算精度高，为轮毂的设计与优化提供理论基础。

关键词：静强度；轮毂；有限元；等效模型；边界条件

中图分类号：TM614 文献标识码：A 文章编号：1674-1161（2017）01-0028-05

轮毂是风力发电机组中连接叶片与主轴的关键部件，结构及形状复杂，需要承受异常复杂的交变载荷条件，因此对其强度及寿命的要求极为严格。轮毂连接叶片根部和风机主轴，叶片上承受推力、扭矩、弯矩等复杂的交变载荷，再通过变桨轴承作用在轮毂上，最后经轮毂传递给主传动系统。轮毂结构的强度计算和疲劳计算均属于复杂的工程实际问题。利用现有的工程力学知识和弹性力学理论很难准确地对承受复杂载荷的轮毂结构进行受力状态描述，通过理论计算也难以解析轮毂强度、寿命等问题。然而，随着计算机技术的迅猛发展，利用有限元方法求解工程中的近似解应用广泛。

在有限元计算过程中，最重要的是实现物理模型的加载与约束，即物理模型的边界条件。轮毂通过螺栓连接3个变桨轴承与输入主轴，螺栓连接与轴承的过渡使轮毂计算模型成为非常复杂的非线性边界条件。建立螺栓连接的接触与轴承钢球与滚道的接触模型，现有的企业级计算水平难以实现。目前，利用等效轮毂静强度有限元计算边界条件简化计算模型、提高计算效率是轮毂强度计算的难点。提出“主轴—轮毂—轴承—叶片”整体有限元等效模型，对螺栓连接、轴承接触等非线性因素进行等效，实现大型风电轮毂的快速有限元计算。

1 轮毂几何模型与力学模型

图1为某风机厂商的2MW风电机组的轮毂三维模型，其基本尺寸参数见表1，材料属性见表2。轮毂计算的整体几何模型由轮毂、变桨轴承、主轴及叶片构成，详见图2。

轮毂的计算载荷传递涉及到2个坐标系，分别是轮毂坐标系（图3）与变桨轴承坐标系（图4）。在轮毂坐标系中：XNF轮毂轴线方向；ZNF竖直向上；YNF垂直于XNF；XNF，YNF，ZNF符合右手定则，原点位于轮毂中心。在叶片坐标系中：ZB与叶片变桨轴重合；XB垂直于ZB，正向指向塔架方向；YB垂直于叶片轴线和主轴轴线，满足右手定则；原点位于叶根部位。

根据提供的叶片载荷谱计算静强度载荷，并通过坐标变换得到表3。

2 轮毂静强度有限元计算边界条件

轮毂静强度有限元计算边界条件主要是变桨轴承的等效与螺栓连接的等效。变桨轴承的等效是指变桨轴承的钢球与滚道的等效处理；螺栓连接等效是指螺栓头部、螺母与被连接件之间的接触等效处理。

2.1 变桨轴承弹性等效模型

变桨轴承双列四点接触球轴承具有结构复杂、尺寸大、刚度低的特点。若完全按照轴承的实际结构建模，钢球与滚道的接触需要进行极其细小的网格划分，且200多个钢球与滚道的接触会导致模型收敛困难，计算效率极低，因此对变桨轴承钢球与滚道的接触的等效处理至关重要。

Daidie A等采用非线性弹簧单元模拟滚动体对轴承进行弹性等效处理。具体等效方式为：以变桨轴承内外圈四沟道曲率中心点C1，C2和C3，C4分别作为端点建立2根弹簧单元，根据Hertz接触公式计算接触椭圆长短半轴，并通过刚性杆联接的形式将弹簧单元端点与沟道上Hertz接触区域内的节点进行耦合，结果如图5所示。

用非线性弹簧单元进行轴承的等效处理能够较为准确地模拟轴承对载荷的传递，反映轴承的受力状态；但在对轮毂拓扑优化时，此种建模方式中的大量非線性弹簧单元会造成迭代步骤多、计算量庞大、收敛困难等不利结果。基于上述分析，提出通过刚性杆模拟滚动体与沟道接触的变桨轴承等效方案，具体为：在每个滚动体的中心建立质量点单元，以刚性杆联接的方式将质量点与各沟道赫兹接触区域内的节点进行耦合，以此来模拟滚动体与轴承内外圈的接触（如图6所示）。

通过Hertz接触公式计算赫兹接触椭圆的长短半轴尺寸，Hertz点接触理论的基本计算公式为：

式中：F（ρ）为接触体的曲率函数，表示曲率差；■ρ为曲率和；α，b为接触椭圆长短半轴；α*，b*是与F（ρ）有关的量纲为1的参数；ξ1，ξ2为材料泊松比；E1，E2为材料弹性模量；Q为法向载荷。

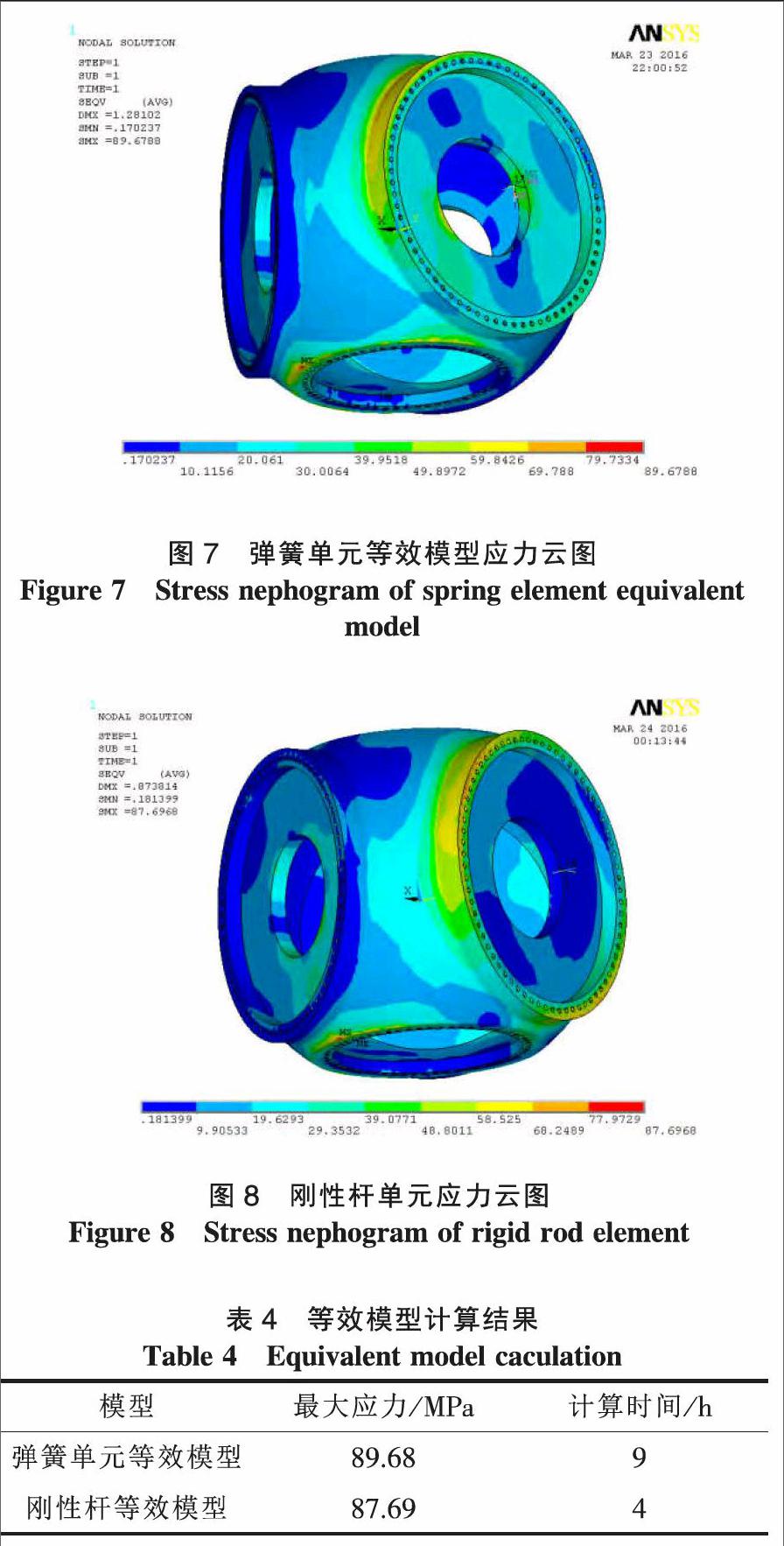
变桨轴承等效处理的目的是实现轴承对载荷的正确传递，因此基于变桨轴承弹簧单元等效模型及刚性杆联接等效模型，分别建立轮毂-轴承-叶片整体模型，采用有限元法对现有2 MW轮毂进行静强度分析。基于单一因子法，只考虑模型中变桨轴承等效模型的不同，其载荷及边界条件相同，提取2种等效模型下轮毂的应力云图，结果如图7—8所示。

2种模型的结果对比如表4所示。

根据求解结果，得出如下结论：1）两种模型中轮毂最大应力出现的位置均在轮毂靠近主轴侧及轮毂法兰根部部位，最大变形位置均出现在轮毂法兰顶部位置。2）与弹簧单元等效模型相比，轴承刚性杆等效模型计算结果中轮毂最大应力误差为2.2%，表明刚性杆等效模型可以起到弹簧单元等效模型中的弹性约束效果。3）刚性杆等效模型的计算时间节省一半，计算效率大幅提高。

在综合考虑计算结果准确度及计算效率的基础上，通过刚性杆模拟滚动体构建变桨轴承弹性等效模型的弹性约束方案，能够较为准确地模拟轴承对载荷的传递。

3.2 螺栓联接弹性等效模型

螺栓联接作为风机轮毂中的一种重要联接方式，其联接面接触问题求解属于复杂的非线性接触问题。在轮毂结构设计模型中完全建立螺栓几何实体，具有计算规模大、计算效率低等问题。一般的做法是对螺栓联接做简化处理，同时对螺栓施加预紧力。为进行有效求解，建立合理的螺栓等效模型非常重要。

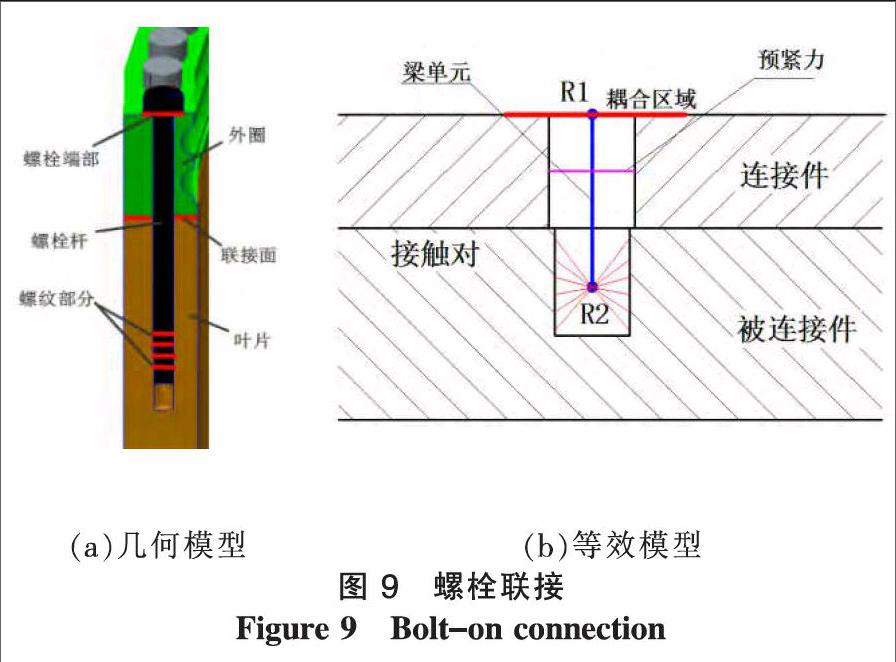
为模拟螺栓联接处载荷传递状态，在“轮毂-轴承-叶片”整体拓扑优化模型中，利用梁与连接件和被连接件刚性联接，建立轴承与轮毂和叶片的螺栓联接等效模型。采用能同时承受轴向力、剪力、弯矩和扭矩的一维复杂梁单元模拟螺栓实体，将螺母与螺栓孔接触区域耦合在螺栓端部中心点R1处，螺栓螺纹接触区域耦合在螺纹接触区域的几何中心点R2处，通过R1，R2点建立梁单元；两连接件联接面之间建立接触对，同时在梁单元上创建梁截面，并施加预紧力模拟螺栓预紧效果。螺栓联接几何模型和等效模型如图9所示。

基于梁单元的螺栓联接等效模型，以“轮毂-轴承-叶片”整体拓扑优化模型中的轴承外圈与叶片螺栓联接为例，对其进行有限元计算，提取轴承外圈螺栓应力，结果如图10所示。其最大应力为572.58 MPa。

运用VDI2230高强度螺栓联接计算标准，对轴承外圈与叶片螺栓联接进行强度计算。

螺栓最大总拉力为：

FSmax=FMzul+Φen*×FAmax=453 516.7（N）（5）

螺栓最大拉伸应力为：

σzmax=FSmax/AS=55.1（MPa）（6）

最大扭转应力为：

τmax=MG/WP （7）

螺栓的实际计算应力为：

式中：FMzul为装配预紧力；FAmax为最危险螺栓所受最大轴向载荷；Φen*为偏心夹紧与偏心载荷下的载荷系数；AS为螺纹应力截面面积，AS=817 mm2；MG为螺纹扭矩；WP为螺纹横截面的极性阻力矩。

通过对螺栓联接的有限元计算结果与理论计算结果进行对比可知，有限元模型中轴承外圈螺栓应力为572.581 MPa，理论计算得到的轴承外圈螺栓实际计算应力为576.45 MPa，误差为0.67%。可见有限元分析结果与理论分析结果基本一致，利用梁单元模拟螺栓联接可以准确模拟螺栓对载荷的传递。

在“轮毂-轴承-叶片”整体拓扑优化模型中，利用刚性杆建立轴承弹性等效模型，采用梁单元建立螺栓联接等效模型，以保证轮毂结构优化模型中优化区域边界为弹性约束，同时保证载荷传递准确性，提高计算效率。