打破数学复习课“讲练结合”的沉闷

杨丽娟

摘 要：初中数学复习课的主要任务是将所学的知识系统化，让学生灵活运用所学的知识解决问题. 初中数学复习课中，可以借题梳理基础知识，归纳本质问题的解法；提炼基本图形，诠释“数形结合”思想；层层推进问题设计，融合多重知识；解决实际问题，在完整结构中体现函数味，以此打破数学复习课“讲练结合”的沉闷.

关键词：数学复习课；梳理知识；数形结合；融合知识；解决问题

《义务教育数学课程标准（2011年版）》指出：“义务教育阶段数学课程的设计，充分考虑本阶段学生数学学习的特点，符合学生的认知规律和心理特征，有利于激发学生的学习兴趣，引发学生的数学思考；充分考虑数学本身的特点，体现数学的实质.”[1]初中数学复习课的主要任务是将所学的知识系统化，让学生灵活运用所学的知识解决问题.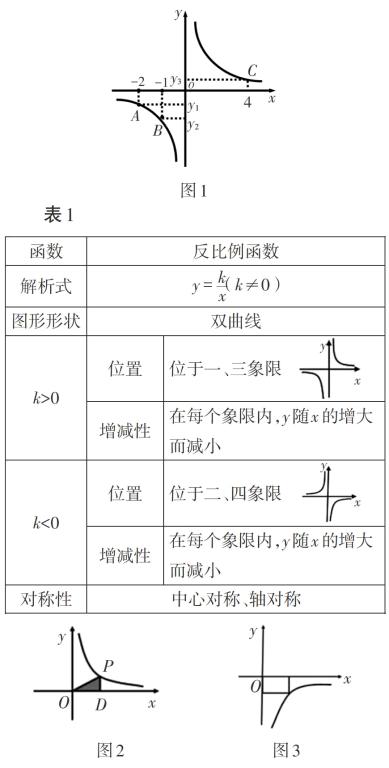

2016年12月8日江苏省中小学“师陶杯”教科研论文颁奖综合学术活动在南通市举行，笔者进行“反比例函数复习”的课堂教学展示，这是人教版八年级下册的内容，此前学生已经系统学习了一次函数，本节课体会反比例函数的意义，能根据已知条件确定反比例函数的表达式；根据反比例函数的图象和关系式 [y=kx] （k为常数，k≠0）加深理解其性质，能与正比例函数进行联系与区别；经历“问题情境——建立模型——解释、应用与拓展”的过程，感受数形结合的思想方法. 结合“反比例函数复习”的课堂教学，对如何优化数学复习课的教学，打破复习课“讲练结合”的沉闷有以下感悟.

一、借题梳理基础知识 归纳本质问题的解法

复习课覆盖的“基础知识”，教师往往都是通过归纳成条文或画图表概括来梳理，这种做法教师津津乐道，学生却感觉枯燥乏味，难以激发学习热情.所以精选系列简单的典型练习，通过问题呈现反比例函数的定义和一般形式以及反比例函数的图象与性质，并通过针对性的讲解，归纳本质问题的解法，以增强知识点之间的融会贯通与理解.

设计意图 《史记》认为由易及难是善问的标志.开始就高难度的问题会把学生难倒、丧失信心；若先设置一些简单问题做铺垫，让学生尝到解决问题的乐趣，再逐渐加大难度，学生比较容易适应.在教学过程中精心设计一组有联系的、层层推进的问题，是激发学生积極思考、深入探究、系统掌握知识、培养思维能力的重要手段，学生通过这样的课堂教学，能更好地建立知识体系，灵活解决问题.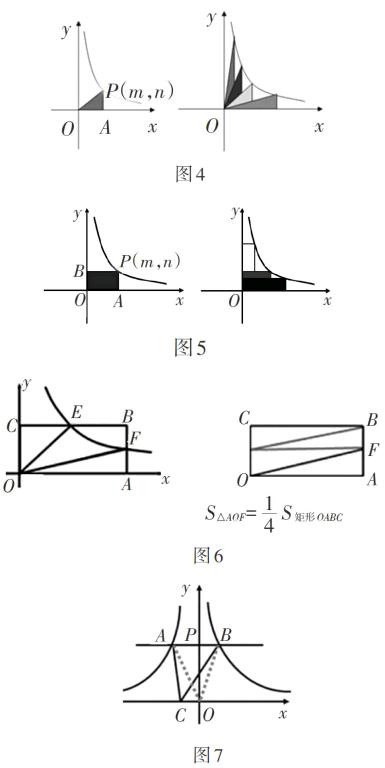

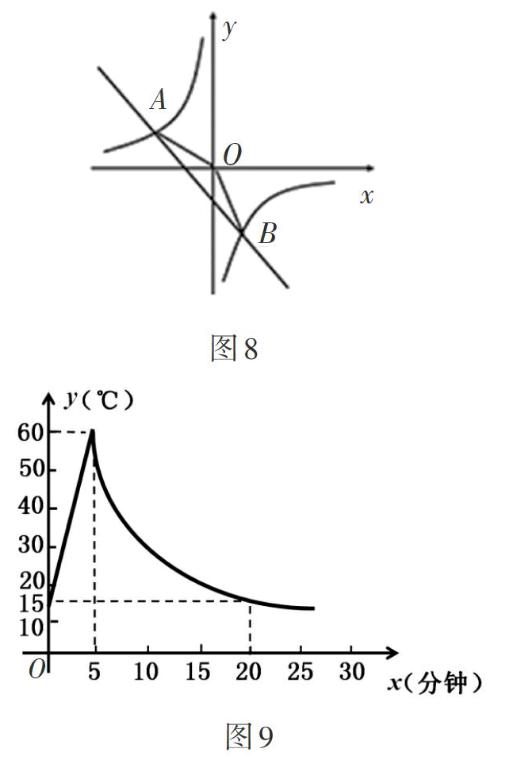
例2问题（1），由点A（-2，1）求得反比例函数[y=mx]的表达式为[y=-2x，]由反比例函数[y=-2x]可知点B的坐标为（1，-2），从而得到一次函数y = kx+b的表达式，学生练习基本没有难度；问题（2），用割补法求面积，可以y轴为分界将△AOB分成左右两个三角形，也可以x轴为分界将△AOB分成上下两个三角形，这题解法明确，但学生计算有问题，设计本题巩固解题方法，提高计算能力；问题（3），方程组中的两个方程，其实就是题中两个函数表达式y = kx+b与[y=mx]，解方程组就是求两函数的交点坐标，这题利用“数形结合”让学生感受“以形助数”的优越性；问题（4），将不等式[kx+b-mx<0]进行简单变形为[kx+b

通过层层推进问题设计，用精心设计的一系列问题，融合多重知识，通过纵向挖掘、横向加强不同知识点间的联系，优化认知结构，提高数学学习效率.

四、解决实际问题 在完整结构中体现函数味

例3 制作一种产品，需先将材料加热到60℃后再进行操作.设该材料温度为y（℃），从加热开始时间计为x（分钟）.据了解，加热时，温度y与时间x成一次函数关系；停止加热进行操作时，温度y与时间x成反比例关系（如图9）.已知该材料在操作加工前的温度为15℃，加热5分钟后温度达到60℃.

（1）分别求出将材料加热和停止加热进行操作时，y与x的函数关系式；

（2）根据要求，当材料的温度低于15℃时，须停止操作，那么从开始加热到停止操作，共经历了多少时间？

设计意图 章建跃博士在《数学概念的理解与教学》中说：“现在的数学概念教学很不尽如人意，一是只在代数的形式化变形及工具运算上下功夫，二是与平面几何知识点拼凑、叠加，成为一种数学游戏，使得很多函数题目的函数味道很淡.”[2]函数味就是在解决问题的过程中，关注函数变量的对应关系，在运动变化的核心内涵上做文章，不纠缠于烦琐的代数式变形和计算.

本节复习课，最后用函数解决实际生活中的数学问题，既培养了学生应用数学的能力，又能在完整课堂结构中体现函数味.例3，第（1）小题结合图象，材料加热时，温度y与时间x成一次函数关系，即当0[≤]x[≤]5时，设y与x的函数关系式为：y = kx+b（k≠0），观察图象，利用点（0，15）和点（5，60）求得此函数关系式.停止加热进行操作时，温度y与时间x成反比例关系，即当x>5时，设y与x的函数关系式为：[y=mx]（m≠0），观察图象，利用点（5，60）求得此函数关系式. 第（2）小题，利用第（1）小题求得的两个函数关系式，分别令y=15，得到两个对应的x值，进而求得从开始加热到停止操作共经历了多少时间.

用函数解决实际问题必须结合函数图象，充分挖掘已知条件并将已知条件体现在函数图象中，利用函数图象让学生感受到对应、感受到变化、感受到直观，从而加深对函数的理解.

参考文献：

[1]中华人民共和国教育部.义务教育数学课程标准（2011年版）[M].北京：北京师范大学出版社，2011：3-4.

[2] 朱玉祥. 要把解题教学这盘菜做得更好吃[J].中学数学，2014（7）：38-41.